Linear Search & Binary Search- 3 | Algorithms - Computer Science Engineering (CSE) PDF Download

Iterative implementation of Binary Search

• C++
  // C++ program to implement recursive Binary Search
  #include <bits/stdc++.h>
  using namespace std;
  // A iterative binary search function. It returns
  // location of x in given array arr[l..r] if present,
  // otherwise -1
  int binarySearch(int arr[], int l, int r, int x)
  {
      while (l <= r) {
          int m = l + (r - l) / 2;
          // Check if x is present at mid
          if (arr[m] == x)
              return m;
          // If x greater, ignore left half
          if (arr[m] < x)
              l = m + 1;
          // If x is smaller, ignore right half
          else
              r = m - 1;
      }
      // if we reach here, then element was
      // not present
      return -1;
  }
  int main(void)
  {
      int arr[] = { 2, 3, 4, 10, 40 };
      int x = 10;
      int n = sizeof(arr) / sizeof(arr[0]);
      int result = binarySearch(arr, 0, n - 1, x);
      (result == -1) ? cout << "Element is not present in array"
                     : cout << "Element is present at index " << result;
      return 0;
  }
• C
  // C program to implement iterative Binary Search
  #include <stdio.h>
  // A iterative binary search function. It returns
  // location of x in given array arr[l..r] if present,
  // otherwise -1
  int binarySearch(int arr[], int l, int r, int x)
  {
      while (l <= r) {
          int m = l + (r - l) / 2;
          // Check if x is present at mid
          if (arr[m] == x)
              return m;
          // If x greater, ignore left half
          if (arr[m] < x)
              l = m + 1;
          // If x is smaller, ignore right half
          else
              r = m - 1;
      }
      // if we reach here, then element was
      // not present
      return -1;
  }
  int main(void)
  {
      int arr[] = { 2, 3, 4, 10, 40 };
      int n = sizeof(arr) / sizeof(arr[0]);
      int x = 10;
      int result = binarySearch(arr, 0, n - 1, x);
      (result == -1) ? printf("Element is not present"
                              " in array")
                     : printf("Element is present at "
                              "index %d",
                              result);
      return 0;
  }
• Java
  // Java implementation of iterative Binary Search
  class BinarySearch {
      // Returns index of x if it is present in arr[],
      // else return -1
      int binarySearch(int arr[], int x)
      {
          int l = 0, r = arr.length - 1;
          while (l <= r) {
              int m = l + (r - l) / 2;
              // Check if x is present at mid
              if (arr[m] == x)
                  return m;
              // If x greater, ignore left half
              if (arr[m] < x)
                  l = m + 1;
              // If x is smaller, ignore right half
              else
                  r = m - 1;
          }
          // if we reach here, then element was
          // not present
          return -1;
      }
      // Driver method to test above
      public static void main(String args[])
      {
          BinarySearch ob = new BinarySearch();
          int arr[] = { 2, 3, 4, 10, 40 };
          int n = arr.length;
          int x = 10;
          int result = ob.binarySearch(arr, x);
         if (result == -1)
              System.out.println("Element not present");
          else
              System.out.println("Element found at "
                                 + "index " + result);
      }
  }
• Python3
  # Python3 code to implement iterative Binary
  # Search.
  # It returns location of x in given array arr
  # if present, else returns -1
  def binarySearch(arr, l, r, x):
      while l <= r:
          mid = l + (r - l) // 2;
          # Check if x is present at mid
          if arr[mid] == x:
              return mid
          # If x is greater, ignore left half
          elif arr[mid] < x:
              l = mid + 1
          # If x is smaller, ignore right half
          else:
              r = mid - 1
      # If we reach here, then the element
      # was not present
      return -1
  # Driver Code
  arr = [ 2, 3, 4, 10, 40 ]
  x = 10
  # Function call
  result = binarySearch(arr, 0, len(arr)-1, x)
  if result != -1:
      print ("Element is present at index % d" % result)
  else:
      print ("Element is not present in array")
• C#
  // C# implementation of iterative Binary Search
  using System;
  class GFG {
      // Returns index of x if it is present in arr[],
      // else return -1
      static int binarySearch(int[] arr, int x)
      {
          int l = 0, r = arr.Length - 1;
          while (l <= r) {
             int m = l + (r - l) / 2;
              // Check if x is present at mid
              if (arr[m] == x)
                  return m;
              // If x greater, ignore left half
              if (arr[m] < x)
                  l = m + 1;
              // If x is smaller, ignore right half
              else
                 r = m - 1;
          }
          // if we reach here, then element was
          // not present
          return -1;
      }
      // Driver method to test above
      public static void Main()
      {
          int[] arr = { 2, 3, 4, 10, 40 };
          int n = arr.Length;
          int x = 10;
          int result = binarySearch(arr, x);
          if (result == -1)
              Console.WriteLine("Element not present");
          else
              Console.WriteLine("Element found at "
                                + "index " + result);
      }
  }
  // This code is contributed by Sam007
• PHP
  <?php
  // PHP program to implement
  // iterative Binary Search
  // A iterative binary search
  // function. It returns location
  // of x in given array arr[l..r]
  // if present, otherwise -1
  function binarySearch($arr, $l,
                        $r, $x)
  {
      while ($l <= $r)
      {
          $m = $l + ($r - $l) / 2;
          // Check if x is present at mid
          if ($arr[$m] == $x)
              return floor($m);
          // If x greater, ignore
          // left half
          if ($arr[$m] < $x)
              $l = $m + 1;
          // If x is smaller,
          // ignore right half
          else
              $r = $m - 1;
      }
      // if we reach here, then
      // element was not present
      return -1;
  }
  // Driver Code
  $arr = array(2, 3, 4, 10, 40);
  $n = count($arr);
  $x = 10;
  $result = binarySearch($arr, 0,
                         $n - 1, $x);
  if(($result == -1))
  echo "Element is not present in array";
  else
  echo "Element is present at index ",
                              $result;
  // This code is contributed by anuj_67.
  ?>
• Javascript
  <script>
  // Program to implement recursive Binary Search
  // A recursive binary search function. It returns
  // location of x in given array arr[l..r] is present,
  // otherwise -1
   function binarySearch(arr, l, r, x)
  {
      if (r >= l) {
           mid = l + Math.floor((r - l) / 2);
          // If the element is present at the middle
          // itself
          if (arr[mid] == x)
              return mid;
          // If element is smaller than mid, then
          // it can only be present in left subarray
          if (arr[mid] > x)
              return binarySearch(arr, l, mid - 1, x);
          // Else the element can only be present
          // in right subarray
          return binarySearch(arr, mid + 1, r, x);
      }
      // We reach here when element is not
      // present in array
      return -1;
  }
      arr =new Array(2, 3, 4, 10, 40);
      x = 10;
      n = arr.length;
      result = binarySearch(arr, 0, n - 1, x);
  (result == -1) ? document.write("Element is not present in array")
                 : document.write ("Element is present at index " + result);
  // This code is contributed by simranarora5sos
  </script>

Output: Element is present at index 3

Time Complexity: The time complexity of Binary Search can be written as
T(n) = T(n/2) + c
The above recurrence can be solved either using the Recurrence Tree method or Master method. It falls in case II of the Master Method and the solution of the recurrence is Theta(Logn).
Auxiliary Space: O(1) in case of iterative implementation. In the case of recursive implementation, O(Logn) recursion call stack space.
Algorithmic Paradigm: Decrease and Conquer.

Note: Here we are using

int mid = low + (high – low)/2;
Maybe, you wonder why we are calculating the middle index this way, we can simply add the lower and higher index and divide it by 2.
int mid = (low + high)/2;
But if we calculate the middle index like this means our code is not 100% correct, it contains bugs.
That is, it fails for larger values of int variables low and high. Specifically, it fails if the sum of low and high is greater than the maximum positive int value(2³¹ – 1 ).
The sum overflows to a negative value and the value stays negative when divided by 2. In java, it throws Array Index Out Of Bound Exception.
int mid = low + (high – low)/2;
So it’s better to use it like this. This bug applies equally to merge sort and other divide and conquer algorithms.

Linear Search vs Binary Search

Prerequisite:

• Linear Search
• Binary Search

1. A linear search scans one item at a time, without jumping to any item .

• The worst case complexity is  O(n), sometimes known an O(n) search
• Time taken to search elements keep increasing as the number of elements are increased.

2. A binary search however, cut down your search to half as soon as you find middle of a sorted list.

• The middle element is looked to check if it is greater than or less than the value to be searched.
• Accordingly, search is done to either half of the given list

Important Differences

• Input data needs to be sorted in Binary Search and not in Linear Search
• Linear search does the sequential access whereas Binary search access data randomly.
• Time complexity of linear search -O(n), Binary search has time complexity O(log n).
•  Linear search performs equality comparisons and Binary search performs ordering comparisons

Let us look at an example to compare the two:
1. Linear Search to find the element “J” in a given sorted list from A-X

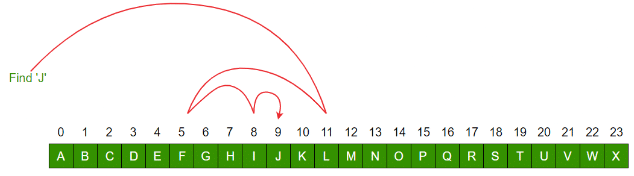
2. Binary Search to find the element “J” in a given sorted list from A-X