Simple Harmonic Motion & Uniform Circular Motion | Physics for JAMB PDF Download
In this article we are going to explain the statement “Uniform Circular motion can be interpreted as a SHM.”.
If we tie a stone to the end of a string and move it with a constant angular speed in a horizontal plane about fixed point, the stone would perform a uniform circular motion in the plane. If we observe the stone sideways, the stone will appear to perform a to and fro motion along the horizontal line with the other end of the string as the midpoint.
Similarly, the projection of the motion or the shadow of the stone would appear to perform a to and fro motion perpendicular to the plane of the circle. Similar case was observed by Galileo, who discovered the four principle moons of the planet Jupiter moved back and forth relative to the planet, executing a simple harmonic motion.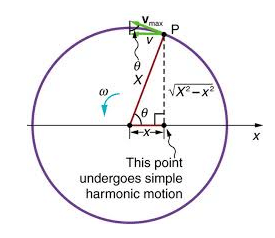
In the figure given above we see the motion of a particle P executing a uniform circular motion or radius A with a constant angular speed ω. We can see that, at any time t, the position of the particle is ωt + φ where φ is the angular position of the particle in the given circle at any time t.
We define the projection of the particle on the X-axis in terms of another particle denoted by a variable Q. The projection of the particle P on the X- axis can be given as,
x(t) = A cos (ωt + φ)
The above expression gives us the position vector of the projection of particle P, that is, the position vector of particle Q, which is undergoing simple harmonic motion. The expression gives the position vector of particle Q at any time t.
Approach To Solve Problems on Simple Harmonic Motion
Suppose there are two particles A and B executing simple harmonic equation given below: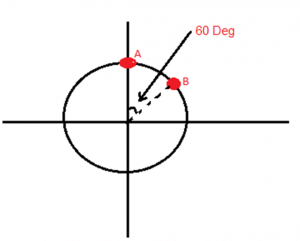
XA = A sin (ωt) XB = A sin ( ωt + π3)
We have to calculate the time after which these two particles will meet for the first time. According to the given equation the system can be represented as below: If we analyze the projection of A and B we can say that both will meet somewhere when B is in fourth quadrant and A is first quadrant. But since both are rotating with same angular speed so angle between them will remain the same. So suppose they meet after A has moved an angle θ. It is shown in the figure below: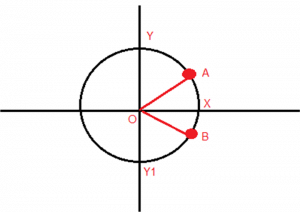
As A and B have same projection on x-axis
so, ∠AOX = ∠BOX …… (1)
And we know, ∠AOB = π3 ……(2)
Using (1) and (2) we have, ∠AOX = π6
From this we conclude that the angle moved by A is π3 also its angular speed is ω.
So time taken can be calculated as: t = π3ω s
Similarly we can say the period of oscillation is 2πω s. A similar question could be: after what time they will have same velocity for the first time? For this if we consider the above situation the magnitude of velocity will be equal but their direction is different so velocity cannot be equal. So for this case we analyze we can say that B will be somewhere in the third quadrant and A in fourth quadrant. Also their displacement from the mean position will be same in magnitude.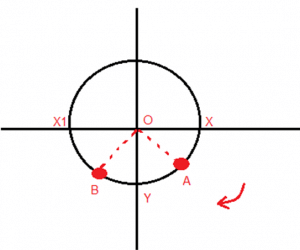
As the displacement should be equal in magnitude
so ∠AOY = ∠BOY ……(3)
And we know, ∠AOB = π3 ……(4)
Using (3) and (4) we get, ∠AOY = π6
So total angle covered by A = π − π6
= 7π6
Time taken = 5π6ω s
We can deal with several other examples of simple harmonic motion.
We can conclude that, if a particle moves in a uniform circular motion, its projection can be said to move in a simple harmonic motion, where the axis of oscillation is the diameter of the circle or in other words, simple harmonic motion is the projection of uniform circular motion along the diameter of the circle on which the circular motion is taking place.
|
261 videos|249 docs|232 tests
|
FAQs on Simple Harmonic Motion & Uniform Circular Motion - Physics for JAMB
| 1. What is simple harmonic motion? |  |
| 2. What are the key characteristics of simple harmonic motion? |  |
| 3. How is uniform circular motion related to simple harmonic motion? |  |
| 4. What is the difference between simple harmonic motion and uniform circular motion? |  |
| 5. How can simple harmonic motion and uniform circular motion be observed in real-life situations? |  |



















