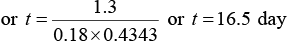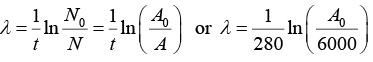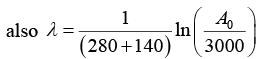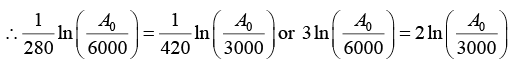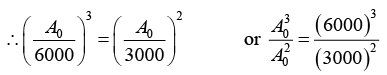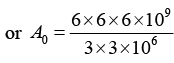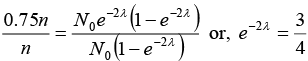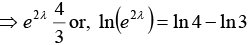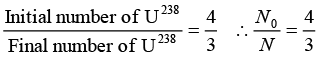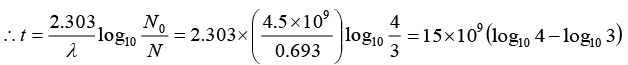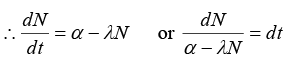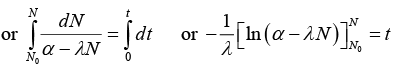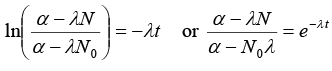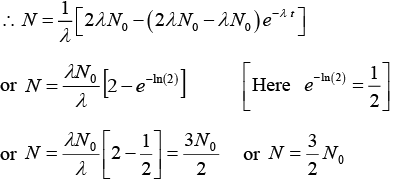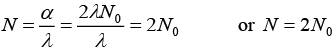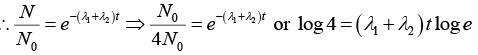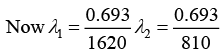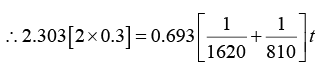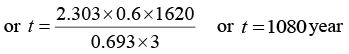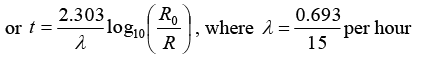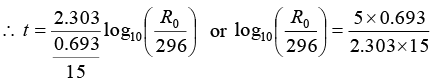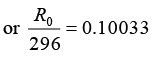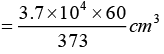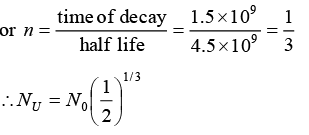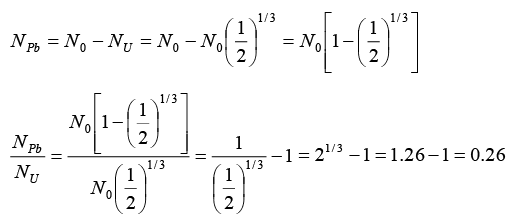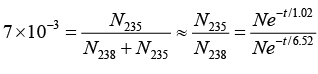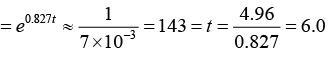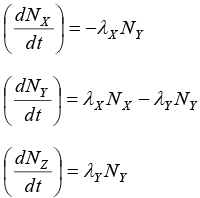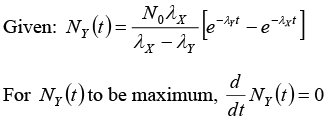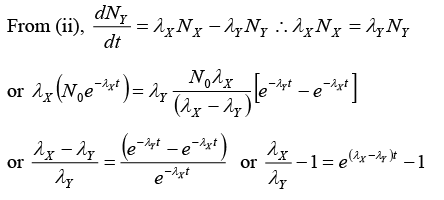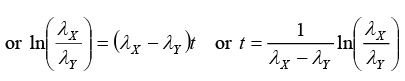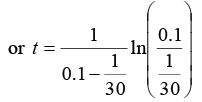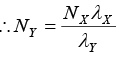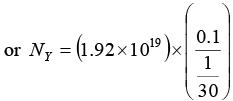Radioactive Decay: Assignment | Modern Physics PDF Download
Q.1. The half life of radioactive radon is 3.8 day. Find the time at the end of which (1 / 20)th of the radon sample will remain undecayed. (Given log10 e = 0.4343)
N = N0e-λ/t where λ = 0.693/3.8 = 0.18
N0/20 = N0e-018t or log10 20 = 0.18 x t x log10 e
or 1.3 = 0.18 x 0.4343 x t
Q.2. A 280 day old radioactive substance shows an activity of 6000 dps, 140 day later its activity becomes 3000 dps. What was its initial activity?
For radioactive disintegration,
or A0 = 24 x 103 or A0 = 24000
∴ Initial activity = 24000 dps
Q.3. A radioactive sample emits nβ -particles in 2 sec. In next 2 sec it emits 0.75nβ -particles. What is the mean life of the sample? Given ln 2 = 0.6931 and ln 3 = 1.0986
Let N0 be the initial number of nuclei. So, after 2 seconds amount remaining = N0e-2λ
∴ Amount dissociated, n = N0(1 - e-2λ) ......(i)
Again after 2 seconds amount remaining = N0e-2λ e-2λ
∴ Amount dissociated, 0.75n = N0e-2λ - N0e-2λ e-2λ
⇒ 0.75 = N0e-2λ (1 - e-2λ) .......(ii)
Solving equations (i) and (ii)
or, 2λ = 2 ln 2 - ln 3 or, 2λ = 2 x 0.6931-1.0986 or, λ = 0.1438sec-1
∴ Mean life = 1/λ = 6.954 second or mean life = 7 second
Q.4. In an ore containing uranium, the ratio of U238 to Pb206 nuclei is 3. Calculate the age of the ore, assuming that all the lead present in the ore is the final stable product of U238 Take the half-life of U238 to be 4.5 x 109 year.
= 15 x 109(0.6021 - 0.4771) = 15 x 109 x 0.1250 = 1.875 x 109 year
Q.5. Nuclei of a radioactive element A are being produced at a constant ratea α. The element has a decay constant λ. At time t = 0 , there are N0 nuclei of the element.
(a) Calculate the number N of nuclei of A at time
(b) If α = 2N0λ, calculate the number of nuclei of after one half-life of A, and also the limiting value of N as t → ∞
Nuclei of a radioactive element A are being produced at a constant ratea .
Decay constant of element = λ ,
At t = 0 , nuclei of element present N0
(a) Number N of nuclei of A at time t :
Net rate of formation of nuclei of element A = dN/dt
or α - λN = e-λt(α - λN0) or N = 1/λ [α - (α - (α - N0λ)e-λt] ........(i)(b) (i) If α = 2λN0, t = half life = In(2)/λ
(ii) when t → ∞ and α = 2λN0
Q.6. A radioactive material decays by simultaneous emission of two particles with respective half-lives 1620 and 810 year. Find the time, in year, after which one-fourth of the material remains.
∵ N/N0 = e-λt
There is a simultaneous emission of two particles
Q.7. A small quantity of containing Na24 radio nuclide (half life = 15 hour)of activity 1.0 micro curie is injected into the blood of a person A sample of the blood of volume 1cm3 taken after 5 hour shows an activity of 296 disintegration per minute. Determine the total volume blood in the body of the person. Assume that radioactive solution mixes uniformly in the blood of the person.
(1curie = 3.7 x 1010 disintegration per second)
For radioactive decay, R = R0e-λt or (-λt) = In R/R0
Half life (T) of the radio nuclide Na24 = 15 hour
Volume of blood = 1 cm3 taken as a sample
After 5 hour, R = 296 dpm in the blood sample.
or R0 = 296 x 1.26 = 373dpm
or R0 = 373/60 dps
Activity of one micro curie 10-6 curie = 3.7 x 104 dps
If activity is (373/60), volume of blood 1 cm3
If activity is dps 3.7 x 104 dps volume
∴ Volume of blood = 5951.7 cm3 or Volume of blood = 5.95litre
∴ Total volume of blood in the body of person is 5.95 litre.
Q.8. A radioactive sample of 238U decays to Pb through a process for which the half-life is 4.5 x 109 year. Find the ratio of number of nuclei of Pb to 238U after a time of 1.5 x 109 year. Given (2)1/3 = 1.26.
Radio of number of nuclei of Pb to U238.
U238 decays and Pb is formed through the radioactive process.
N = N0(1/2)n where = N0 Initial number of radioactive material
N = Number of radioactive material left, n = Number of half lives
Q.9. In the mixture of isotopes normally found on the earth at the present time, 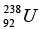 has an abundance of 99.3% and
has an abundance of 99.3% and 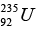 has an abundance of 0.7%. The measured lifetimes of these isotopes are 6.52 x 109 years and 1.02 x 109 years, respectively. Assuming that they were equally abundant when the earth was formed, the estimate age of the earth, in years.
has an abundance of 0.7%. The measured lifetimes of these isotopes are 6.52 x 109 years and 1.02 x 109 years, respectively. Assuming that they were equally abundant when the earth was formed, the estimate age of the earth, in years.
If the number of 92U238 nuclei originally formed is N, the number present now is N238 = Ne-t/T = Ne-t/6.562
where t is elapsed time in units of 109 year and T is life time of U. Since the number of 92U235 nuclei originally formed. The number now present is N235 = Ne-t/1.02
The present abundance of 92U235 is
That is, the elapsed time is t = 6.0x109 yr.
Q.10. A radioactive nucleus X decays to a nucleus Y with a decay constant λX = 0.1s-1. Y further decays to a stable nucleus Z with a decay constant λY = (1/30)s-1 Initially there are only X s nuclei and their number is N0 = 1020.
Set, up the rate equations for the populations of X , Y and. Z. The Populations of Y nucleus as a function ‘of time is given by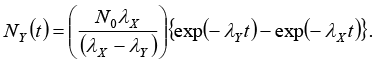
Find the time at which NY is maximum and determine the populations of X and Z at that instant.
Radioactive nucleus X decays to a nucleus Y
Y further decays to a stable nucleus Z
Initially there are only X nuclei and there number is N0 = 10
(i) Rate equations:
At an instant t ,
Let number of nuclei of Y = NY and number of nuclei of = N2
∴ Rate equations of populations of X , Y and Z are
(ii) Time t at which NY is maximum:
or t = 15ln(3) or t = 16.48 sec
(iii) Populations of X and Z when NY is maximum:
NX = N0e-λxt or Nx =(10)20e-(0.1)(16.48)
or NX = 1.92 x 1019
Since λXNX = λYNY according to equation (iv),
or NY = 5.76x1019
Again NZ = 1020 - (1.92 x 1019) - (5.67 x 1019)
or NZ = 1019 [10 - 1.92 - 5.76]
NZ = 2.32 x 1019
Hence (i) Rate equations for populations X, Y, Z are given in equations (i), (ii) and (iii)
(ii) Time at which NY is maximum = 16.48sec
(iii) Population of X = NX = 1.92 x 1019
Population of Z = NZ = 2.32 x 1019
|
37 videos|17 docs|19 tests
|
FAQs on Radioactive Decay: Assignment - Modern Physics
| 1. What is radioactive decay? |  |
| 2. What is the significance of radioactive decay? |  |
| 3. How does radioactive decay work? |  |
| 4. What are the different types of radioactive decay? |  |
| 5. How is radioactive decay measured? |  |