Rotational Dynamics: Assignment | Mechanics & General Properties of Matter - Physics PDF Download
Q.1. A wooden log of mass M and length L is hinged by a frictionless nail at O . A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system, immediately after the collision, about O.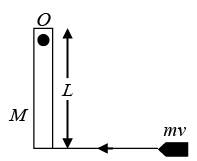 Ans: A bullet of mass m strikes the wooden log of mass M and length L and sticks to it. Angular momentum of the system, about point O , remains conserved
Ans: A bullet of mass m strikes the wooden log of mass M and length L and sticks to it. Angular momentum of the system, about point O , remains conserved
Initial angular momentum = Final angular momentum
∴ mvL= Ioω ....(i)
Q.2. (Inelastic collision): A mass m travels at speed v0 perpendicular to a stick of mass m and length ℓ, which is initially at rest. The mass collides completely inelastically with the stick at one of its end and sticks to it. What is the resulting angular velocity of the system by
(a) choosing the origin to be fixed Point that coincides with the location of the CM right when the collision happens (that is, the point /4 from the end of the stick).
(b) choosing the origin to be the fixed point that coincides with the initial centre of the stick.
(c) choosing the origin to be the CM of the system.
Ans: The first thing to note is that the CM of the system is ℓ/4 from the end, as shown in figure. After the collision, the system rotates about the CM as the CM moves in straight line.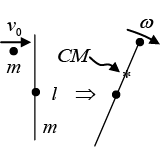 Conservation of momentum quickly tells us that the speed of the CM is v0/2. Also, using the parallel - axis theorem, the moment of inertia of the system around the CM is
Conservation of momentum quickly tells us that the speed of the CM is v0/2. Also, using the parallel - axis theorem, the moment of inertia of the system around the CM is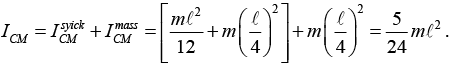
There are now many ways to proceed, depending on what point we choose as our origin. (a) Choose the origin to be the fixed point that coincides with the location of the CM right when the collision happens (that is, the point ℓ/4 from the end of the stick). Conservation of L says that the initial L of the ball must equal the final L of the system.
This gives
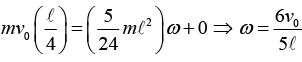
The zero here comes from the fact that the CM of the stick moves directly away from the origin,
(b) Choose the origin to be the fixed point that coincides with the initial centre of the stick. Then conservation of L gives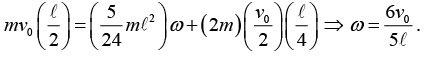
The right-hand side is the angular momentum of the system relative of the CM, plus the angular momentum (relative to the origin) of a point mass of mass 2m located at the CM.
(c) Choose the origin to be the CM of the system. This point moves to the right with speed v0/2 . Along the line a distance ℓ/4 below the top of the stick. Relative to the CM, the mass m moves to the right, and the stick moves to the left, both with speed v0/2. Conservation of L gives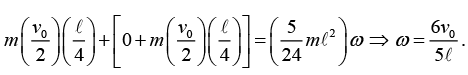
The zero here comes from the fact that the stick initially has no L around its center. A fourth reasonable choice the origin is the fixed point that coincides with the initial location of the top of the stick. You can work this one out for practice.
Q.3. (Elastic Collision): A mass m travels perpendicular to a stick of mass m and length l , which is initially at rest. At what location should the mass collide elastically with the stick, so that the mass and the center of the stick move with equal speeds after the collision?
Ans: Let the initial speed of the mass be v0 . We have three unknowns in the problem (see figure below), namely the desired distance from the middle of the stick, h ; the final (equal) speed of the stick and the mass, v ; and the angular speed of the stick, w . We can solve for these three unknowns by using our three available conservation laws:
Conservation of p:
mv0 = mv + mv ⇒ v = v0/2 Conservation of E: Remembering that the energy of the stick equals the energy of the rotational motion around the centre, plus the energy of the effective point mass at the centre, we have
Conservation of E: Remembering that the energy of the stick equals the energy of the rotational motion around the centre, plus the energy of the effective point mass at the centre, we have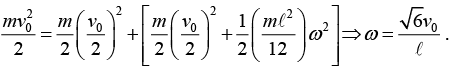
Conservation of L: Let’s pick our origin to be the fixed point in space that coincides with the initial location of the centre of the stick. Then conservation of L gives
Q.4. A disc rolls without slipping along a horizontal surface with velocity u . The disc then encounters a smooth drop of height h , after which it continues to move with velocity v . At all times disc remains in a vertical plane
Show that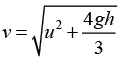
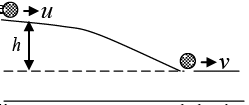
Ans: The total kinetic energy T of the disc on the horizontal surface is
T(initial) = 182 Mu2 + 1/2 Iω2 + Mgh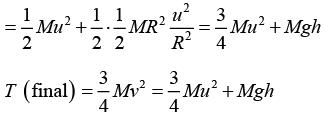
By energy conservation, 3/4 Mv2 = 3/4 Mu2 + Mgh
Solving, 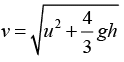
Q.5. Sliding to rolling A ball initially slides without rotating on a horizontal surface with friction See Figure. The initial speed is V0 , and the moment of inertia around the centre is I = βmR2.
(a) Without knowing anything about the nature of the friction force, find the speed of the ball when it begins to roll without slipping. Also, find the kinetic energy lost while sliding.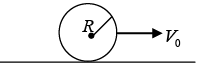
Ans: (a) Define all linear quantities to be positive to the right, and all angular quantities to be positive clockwise, as shown in Figure. Then the friction force Ff is negative. The friction force slows down the translational motion and speeds up the rotational motion.
From conservation of angular momentum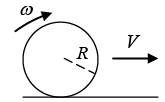 mV0R = Icmω+ mV fR
mV0R = Icmω+ mV fR
For pure rolling case Vf = ωR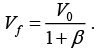 Independent of the nature of Ff.
Independent of the nature of Ff.
Ff can depend on position, time, speed or anything else. The relation a = -βRα, and hence also, will still be true at all times.
Remark: We can also calculate τ and L relative to a dot painted on the ground that is the contact point at a given instant. There is zero torque relative to this point. To find L , we must add the L of the CM and the L relative to the CM. Therefore, τ = dL/dt gives 0 = (d/dt(mvR + βmR2ω, and so a = -βRα , as above and also the relation ωf = Vf/R , the loss in kinetic energy is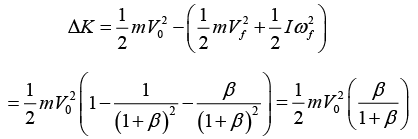
For β ⇢ 0 , no energy is lost, which makes sense. And for β ⇢ ∞ (a spool sliding on its angle), all the energy is lost, which also makes sense, because we essentially have a sliding block which can't rotate.
Q.6. The sphere shown in figure lies on a rough plane when a particle of mass m traveling at a speed v0 collides and sticks with it. If the line of motion of the particle is it a distance h above the plane, find
(a) the linear speed of the combined system just after the collision,
(b) the angular speed of the system about the center of the sphere just after the collision and
(c) the value of h for which the sphere starts pure rolling on the plane. Assume that the mass M of the sphere is large compared to the mass of the particle so that the centre of mass of the combined system is not appreciably shifted from the centre of the sphere.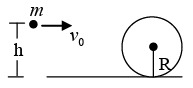 Ans: Take the particle plus the sphere as the system.
Ans: Take the particle plus the sphere as the system.
(a) Using conservation of linear momentum, the linear speed of the combined system v is given by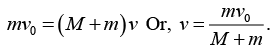 ....(i)
....(i)
(b) Next, we shall use conservation of angular momentum about the centre of mass, which is to be taken at the centre of the sphere ( M >>m) . Angular momentum of the particle before collision is mv0 (h - R). If the system rotates with angular speed ω after collision, then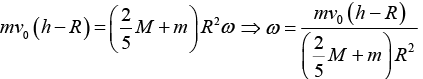
(c) The sphere will start rolling just after the collision if
Q.7. A circular ring of mass M and radius r lies at rest on a smooth horizontal surface. An insect of mass m sits on it and crawls round the ring with a uniform speed v relative to the ring. Obtain an expression for the angular velocity of the ring.
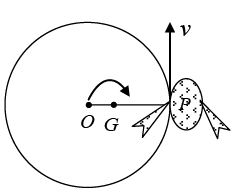 Ans: In Figure, O is the centre of the ring, P the instantaneous position of the insect and G the centre of mass of the system. Suppose the insect crawls around the ring in the counterclockwise sense. The only forces acting in a horizontal plane are the reactions at P which are equal and opposite. Consequently G will not move and the angular momentum about G which was initially zero will remain zero throughout the motion due to its conservation of angular momentum
Ans: In Figure, O is the centre of the ring, P the instantaneous position of the insect and G the centre of mass of the system. Suppose the insect crawls around the ring in the counterclockwise sense. The only forces acting in a horizontal plane are the reactions at P which are equal and opposite. Consequently G will not move and the angular momentum about G which was initially zero will remain zero throughout the motion due to its conservation of angular momentum
m × PG(v - PGω) - IGω = 0 ....(1)
Where w is the angular velocity of the ring.
Now .....(2,3)
.....(2,3)
Using (2) and (3) in (1) and simplifying we obtain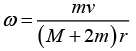 ...(4)
...(4)
Q.8. A cylinder of mass M is suspended through two strings wrapped around it shown in figure
(a) Find the tension T and in the strings and acceleration of cylinder.
(b) The speed of the cylinder as it falls through a distance h.
Ans: The force equation is Mg - 2T= Mα ...(1)
The torque equation is 2TR = Icmα where α = α/r and Icm = MR2/2
Put the value of T = Mα/4 in equation (1) we get α = 2/3 g and T = Mg/6
Using kinematics equation v2 = u2 + 2αs here u = 0, α = 2/3 g,s = h So v = 
Q.9. A rod of mass m and length l is suspended from two massless vertical springs with a spring constants k1 and k2 . If x1 and x2 be the displacements from equilibrium position of the two ends of the rod
(a) Find the kinetic energy of system
(b) Find the total energy of system
Ans:
(a) 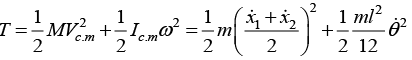
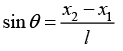 for small oscillation
for small oscillation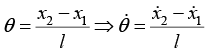 (keep in mind that there is not pure rotation case)
(keep in mind that there is not pure rotation case)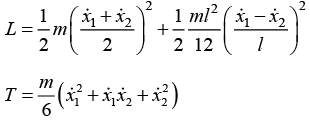
(b) Potential energy is,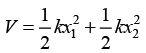
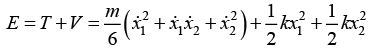
Q.10. A board of mass M, whose upper surface is rough and under surface smooth, rests on a smooth horizontal plane. A sphere of mass m is placed on the board and the board is suddenly given a velocity v0 in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the board and the sphere is μ.
Ans: Let a be the acceleration of block mass M. Let ACM be the acceleration of C.M , of sphere. Let α be the angular acceleration of sphere.
Force Diagram
(i) fk = Mα
α = μmg/M
(ii) fk = mACM
Acm = μg
When pure rolling starts, velocity of points P and Q will become equal.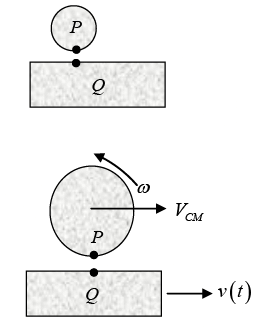 VP = VQ
VP = VQ
VCM + rω = v ....(i)
v(t) = v0 - μm/M gt ….(ii)
VCM (t) = 0 + μgt ....(iii)
ω(T) = 0 + μmgr/ICM ….(iv)
Solving, (i), (ii), (iii) and (iv) we get:
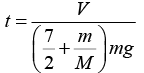
Q.11. A uniform cylinder of radius R is spanned about its axis to the angular velocity ω0 and then placed into a corner . The coefficient of friction between the corner walls and the cylinder is equal to k. How many turns will the cylinder accomplish before it stops?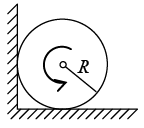
Ans: F.B.D. of cylinders
Force equation:
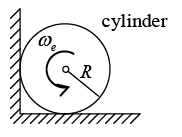 KN + N2 = mg ...(i)
KN + N2 = mg ...(i)
KN2 = N1 .....(ii)
Torque equation about centre of cylinder: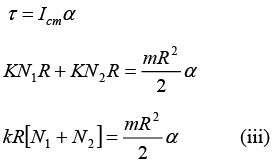
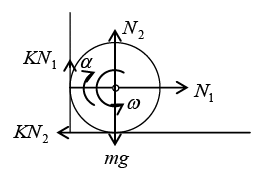 from (i) and (ii): N2 =
from (i) and (ii): N2 = 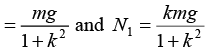
put in (iii): 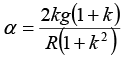
we know:
ω2 = ω02 - 2αθ ⇒ 0 = ω02 - 2αθ turn is given by
turn is given by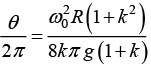
|
61 videos|23 docs|25 tests
|
















