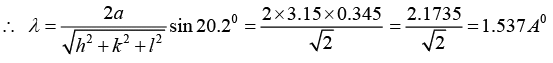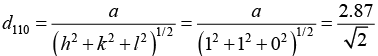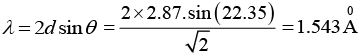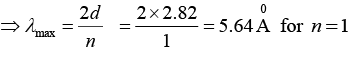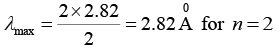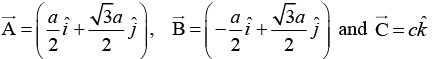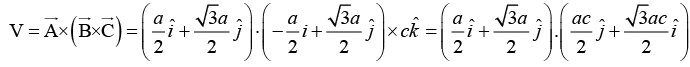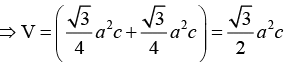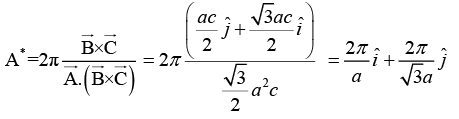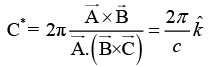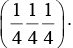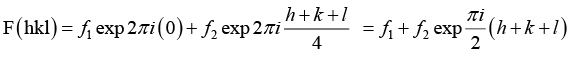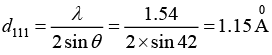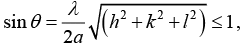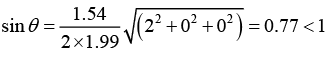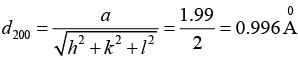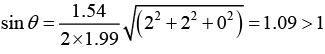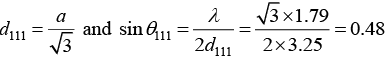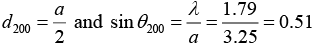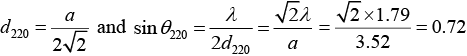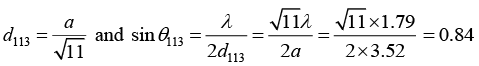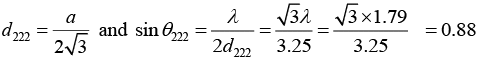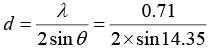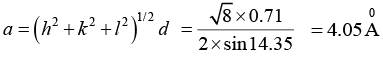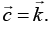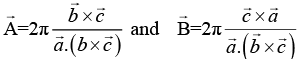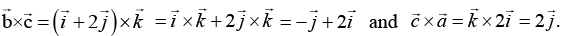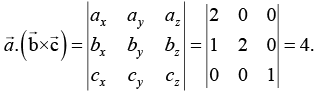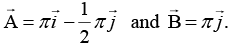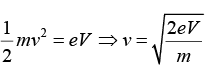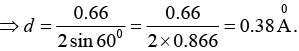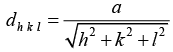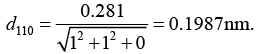X-Ray Diffraction: Assignment | Solid State Physics, Devices & Electronics PDF Download
Q.1. When a crystal is subjected to a monochromatic X - ray beam, the first order diffraction is obtained at an angle of 150. Determine the angle for second and third order when the same X - ray beam is used.
Given n = 1, θ = 150, λ = fixed , θ2 = ?, θ3 = ?
For first order, the Bragg’s equation is 2d sinθ1 = λ
⇒ λ/d = 2sinθ1 = 2 sin150 = 0.518
For second order diffraction, n = 2, the Bragg's equation becomes d sinθ2 = λ
⇒ sinθ2 = λ/d = 0.518
⇒ θ2 = sin-1(λ/d) = sin-1(0.518) = 31.20
Similarly, for third order diffraction, n = 3, the Bragg's equation becomes 2d sinθ3 = 3λ
⇒ sinθ3 = (3/2)(λ/d) =3/2 x 0.518 = 0.777
⇒ θ3 = sin-1(0.777) = 510
Q.2. The lattice parameters of a copper (fcc) is 3.51Å. The first order peak from the (111) plane appears at an angle of 21.70. Find the wavelength of the X - ray used.
For FCC : neff = 4,
Given a = 3.61Å, q= 21.70
The Bragg’s law is
2d sinθ =nλ For 1st order diffraction, n = 1
Q.3. Determine the lattice parameter of a nickel (fcc) if Bragg's angle for its (220) reflection is 38.20 and the wavelength of the X - ray used is 1.54Å.
Given (hkl) = (220), structure is fcc, Bragg's angle θ = 38.20, λ = 1.54Å, a = ?
For a cubic crystal, we know that the interplanar spacing ' d' and the lattice parameter ' a' are related through
Further, from Bragg’s equation, we have 2dhkl sinθhkl = λ
Or
Q.4. A bcc crystal is used to measure the wavelength of some X - ray. The first order Bragg’s angle corresponding to the (110) plane is 20.20. Calculate the wavelength of X-ray if the lattice parameter of the crystal is 3.15Å.
2d sinθ = nλ, n = 1, (110) plane, θ = 20.20, a = 3.15A0
Q.5. X - rays of unknown wavelength are diffracted from an iron sample. The first peak was observed for the (110) plane at 2θ = 44.700. If the lattice parameter of the bcc iron is 2.87Å, determine the wavelength of the X - ray used.
Given: Crystal is bcc, (hkl) ≡ (110) planes, 2θ = 44.700, so that θ = 22.350, a = 2.87Å, λ = ?
For (110) planes, we have
Further, from the Bragg’s equation, we obtain
Q.6. Determine the longest wavelength that can be analyzed by a rock-salt-crystal with interplanar spacing 2.82Å in the first and the second orders of the X - ray diffraction.
Given d = 2.82Å, n = 1, 2 and λmax = ?
We know that the Bragg’s equation is given by 2d sinθ =nλ
Here, λ be maximum, sin θ must be maximum, i.e. (sinθ)max = 1
This given us nλmax = 2d
and
Q.7. The primitive translation vectors of a hexagonal space lattice may be taken as 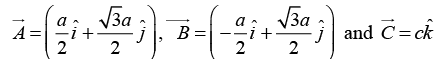 where
where 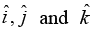 are unit vectors. Determine the primitive translation vectors of the reciprocal lattice.
are unit vectors. Determine the primitive translation vectors of the reciprocal lattice.
Given Direct lattice parameter
Volume of the direct unit cell is given by
Therefore,
Similarly,and
Q.8. Find the geometrical structure factor for an fcc structure in which all atoms are identical. Hence show that for the fcc lattice, no reflection can occur for the partly even and partly odd indices.
General form of the structure factor is given by
...(1)
In an fcc structure, there four atoms in the unit cell. Position coordinates of these atoms in the unit cell are:Substituting these values in equation (1), we get
= f1 + f2 exp πi(h + k) + f3 exp πi (h + l) + f4 exp πi (k + l)
Now, we know that exp(πim) = (-1)m = (-1) if m is odd = (+1) if m is even
For identical atoms, f1 = f2 = f3 = f4 = f (say). Therefore,
F(hkl) = 4f when h k l are odd or all even, and
F(hkl) = 0 when h k l are mixed
Q.9. The diamond structure is formed by the combination of two interpenetrating fcc sub-lattices: the basis being (0 0 0) and 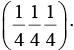 Find the structure factor of the basis and prove that if all indices are even, the structure factor of basis vanishes unless h + k + l = 4n, where n is an integer.
Find the structure factor of the basis and prove that if all indices are even, the structure factor of basis vanishes unless h + k + l = 4n, where n is an integer.
The general form of the structure factor is given by
...(1)
The position coordinates of the atoms in the unit cell are given as: (0 0 0) and
Substituting these values in equation 1,
For identical atoms, f1 = f2 = f (say). Therefore, the structure factor becomeswhen h + k + l = 4n (where n is an integer) = 0, otherwise.
Q.10. In an X - ray diffraction experiment the first reflection from an fcc crystal is observed at 2θ = 840, when Cu, Kα radiation of wavelength 1.54Å is used. Determine the indices of possible reflection and the corresponding interplanar spacing.
Given 2θ = 840 ⇒ q = 420 and n = 1, structure is fcc, λ = 1.54Å (h1k1l1) = ?, d1 = ? ; (h2k2l2) = ?, d2 = ?
We know that the ratio of (h2+k2+l2) value for allowed reflection in fcc are 3, 4, 8,11,12,16,19, 20
where h2 + k2 + l = 3 corresponds to first reflection from (111)
h2 + k2 + l = 4 corresponding to second reflection from ( 200)
h2 + k2 + l = 8 corresponding to third reflection from ( 220) , and so on
Also, Bragg’s law for first order reflection is 2d sinθ = λ
The lattice constant is a = (h2+k2+l2)1/2 dhkl = (1 + 1 + 1)1/2 x 1.15Å = 1.99Å
For allowed reflection
Now, for h2 + k2 + l2 = 4,
This gives us
Now, for h2 + k2 + l2 = 8,
which is not a possible reflection. Thus the possible reflection are (111) and (200), the corresponding interplanar spacing are 1.15Å and 0.996Å.
Q.11. A powder pattern is obtained for an fcc crystal with lattice parameter 3.52Å by using X - rays of wavelength 1.79Å. Determine the lowest and highest reflection possible.
Given Crystal is fcc, a = 3.52Å, λ = 1.79Å, lowest reflection = ?, Highest reflection = ?
We Know that the ratio of (h2 + k2+ l2) values for allowed reflection in fcc are 3 : 4 : 8 :11:12 :16 :19 : 20 respectively.
For (h2+k2+l2) = 3, we have
Similarly, for (h2 + k2 + l2) = 4, we have
For (h2+k2+ l2) = 8, we have
For (h2+k2+ l2) = 11,
For (h2+k2+ l2) = 12,
However, for (h2 + k2 + l2) = 16, the value of d will be greater than 1which is not possible. Thus, the lowest and highest reflections for given l are (111) and ( 222) .
Q.12. The Bragg’s angle corresponding to a reflection for which (h2 + k2 + l2) = 8 is found to be 14.350. Determine the lattice parameter of the crystal if the X - rays of wavelength 0.71Å are used. If there are two other reflection of smaller Bragg’ angle, determine the crystal structure.
Given(h2+k2+l2) = 8, θ = 14.350, λ = 0.71Å, a = ? structure = ?
For the given (hkl) the value of d is
Further, for a cubic system
If there are two other reflection of smaller Bragg’ angle, than lattice is FCC.
Q.13. A two-dimensional lattice has the basis vectors 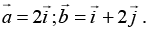 Find the basis vectors of the reciprocal lattice.
Find the basis vectors of the reciprocal lattice.
Let third vector
be parallel to the z -axis, or let
The vector of the reciprocal lattice are
But
Substituting,
Q.14. Electrons are accelerated under 344 V and then reflected from a crystal. The first reflection maxima occur when the glancing angle is 600. Determine the interplanar spacing of the crystal. Given, h = 6.62 x 10-34 Js, e = 1.6 x 10-19C, electron mass, m = 9.1 x 10-31 kg.
Let λ = wavelength, m = the mass of the electron, V = accelerating voltage v = the velocity of the electron (non-relativistic).
The kinetic energy of the electron = 1/2 mv2
At equilibrium,
But⇒ λ = 0.66Å
The Bragg equation for reflection is 2d sinθ =nλ.
Given that n = 1, θ = 600, we have 2d sin600 = λ = 0.66Å
Q.15. Calculate the glancing angle on the plane (1 1 0) of a cube salt (a = 0.281nm) corresponding to the second-order diffraction maximum for X - rays of wavelength
0.071 nm.
From the Bragg’s law, 2d sinθ = nλ ⇒ θ = sin-1(nλ/2d)
The interplanar spacing of (h k l) planes is
∴
Using the value of d, we get, for n = 2,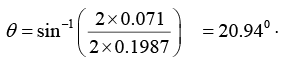
|
91 videos|21 docs|25 tests
|
FAQs on X-Ray Diffraction: Assignment - Solid State Physics, Devices & Electronics
| 1. What is X-ray diffraction and how does it work? |  |
| 2. What are the applications of X-ray diffraction? |  |
| 3. How is X-ray diffraction used in the field of medicine? |  |
| 4. What are the advantages of X-ray diffraction compared to other analytical techniques? |  |
| 5. Are there any limitations or challenges associated with X-ray diffraction? |  |