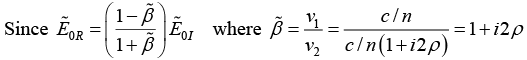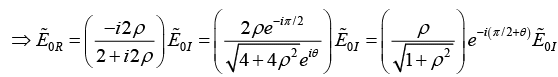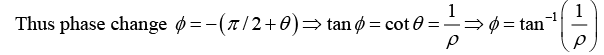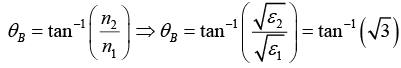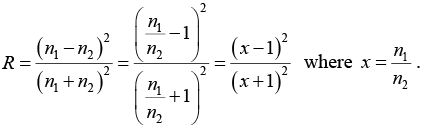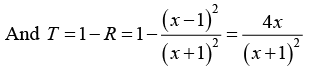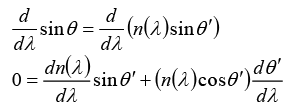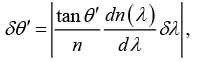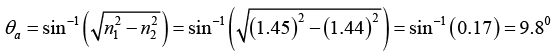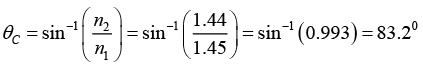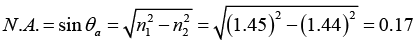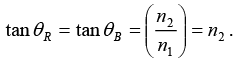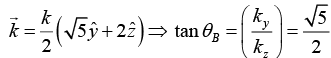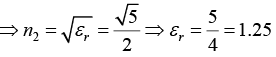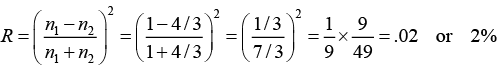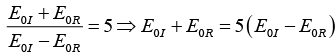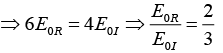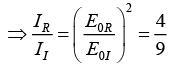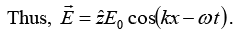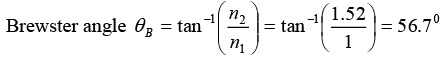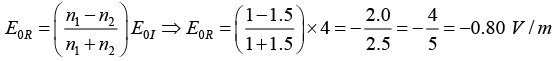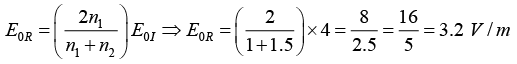Reflection & Transmission at an Interface: Assignment | Electricity & Magnetism - Physics PDF Download
Q.1. A beam of light of frequency ω is reflected from a dielectric-metal interface at normal incidence. The refractive index of the dielectric medium is n and that of the metal is n2 = n(1+ i2ρ) . If the beam is polarised parallel to the interface, then what will be the phase change experienced by the light upon reflection.
where tan θ =ρ.
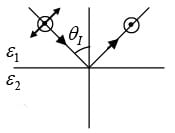
Q.2. A beam of unpolarized light in a medium with dielectric constant ε1 is reflected from a plane interface formed with another medium of dielectric constant ε2 = 3ε1 . The two media have identical magnetic permeability. If the reflected light is plane polarized perpendicular to the plane of incidence, then find the angle of incidence.
⇒ θB = 60°(hence reflected light is plane polarized perpendicular to plane of incidence))
Q.3. Consider interface between two dielectric medium having refractive index n1 and n2 where n1>n2. If electromagnetic wave strikes normal to the interface such that reflection and transmission coefficients are equal then show that n1 = 5.82n2.
Q.4. A beam of light has a small wavelength spread δ λ about a central wavelength λ. The beam travels in a vacuum until it enters a glass plate at an angle θ relative to the normal to the plate, as shown in the figure. The index of refraction of the glass is given by n (λ). Show that the angular spread of the refracted beam is given by
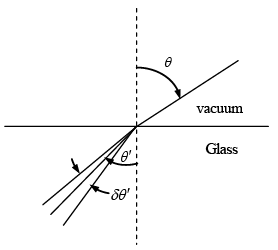
From Snell’s Law, one obtains
sinθ = n(λ )sinθ', since the index of refraction of air is about 1.Now, differentiate both sides with respect to λ
Q.5. For an optical fiber with core and cladding index of n1 = 1.45 and n2 = 1.44, respectively,
(a) What is the maximum acceptance angle in air?
(b) What is the cut-off angle of incidence at core-cladding interface?
(c) What is the numerical aperture of the fiber?
(a)
(b)
(c)
Q.6. Unpolarized light is incident on an air-dielectric interface. The interface is the xy plane, and the plane of incidence is yz plane. The electric field of the reflected light is given by 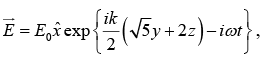 where k is the propagation constant in air and ω is the angular frequency of the light. Assume magnetic permeability μ=μ0. Find the dielectric constant of the second medium.
where k is the propagation constant in air and ω is the angular frequency of the light. Assume magnetic permeability μ=μ0. Find the dielectric constant of the second medium.
Since reflected light is plane polarized, then angle of reflection is Brewester angle
Q.7. (a) A plane electromagnetic wave traveling in free space is incident normally on a glass plate of refractive index 4/3. If there is no absorption by the glass, find its reflectivity.
(b) A plane electromagnetic wave incident normally on the surface of a material is partially reflected. Measurements on the standing wave in the region in front of the interface show that the ratio of the electric field amplitude at the maxima and the minima is 5. Find the ratio of the reflected intensity to the incident intensity.
(a)
(b)
Q.8. An electromagnetic plane wave, propagating in vacuum, has an electric field given by E = E0 cos(kx - ωt) and is normally incident on a perfect conductor at x = 0, as shown in the figure. Immediately to the left of the conductor, find the total electric field E and the total magnetic field B.
For a conductor, the electric field boundary condition at the interface are
The plane wave traveling in the x-direction is polarized (say) in the +z-direction.
There is no component perpendicular to the conductor at the boundary, and thus the first boundary condition implies that the free charge density is 0.
The second boundary condition requires thatThe parallel component of E is polarized in the z-direction, and thus the requirement is
i.e., the incident plus the reflected is equal to the transmitted wave. However, for a perfect conductor, the transmitted wave is 0. Thus, one has
This implies that the electric field to the left of the conductor cancels.
Recall the Poynting vector,which conveniently points in the direction of the electromagnetic wave propagation. Since the electric field (by the convention used above) is polarized in the z-direction, the magnetic field of the incident wave points in the - y direction. However, since the electric field of the reflecting wave points in the - z direction, its magnetic field also points in the - y direction. The magnetic field
magnitude is thus 2E0/c. Hence, E = 0, B= (2E0/c)cos ωt
Q.9. (a) When unpolarised light is incident on a glass plate at a particular angle, it is observed that the reflected beam is linearly polarized. What is the angle of the refracted beam with respect to the surface normal?
(b) A light source is at the bottom of a pool of water (index of refraction of water is 1.33). At what minimum angle of incidence will a ray be totally reflected at the surface?
(a) Since n1 = 1 , n2 = 1.52
Now θR = 180 - 90 - 56.7 = 33.4°
(b) Total internal reflection is when one has a beam of light having all of the incident wave reflected.
Law for Total Internal Reflection, ninside sinθ = noutside,
where ninside = 1.33 and one assumes that the surface has noutside = 1 for air.⇒ θ = sin-1 (1/1.33) sin-1 (0.76) =50°
Q.10. A plane electromagnetic wave traveling in vacuum is incident normally on a nonmagnetic, non-absorbing medium of refractive index (n). The incident (Ei), reflected (Er) and transmitted (Et) electric fields are given as,
If E = 4 V/ m and n = 1.5 then find E0r and E0t
|
82 videos|32 docs|22 tests
|
FAQs on Reflection & Transmission at an Interface: Assignment - Electricity & Magnetism - Physics
| 1. What is the difference between reflection and transmission at an interface? |  |
| 2. How is the amount of reflection and transmission determined at an interface? |  |
| 3. What happens to the reflected and transmitted waves if the angle of incidence is increased? |  |
| 4. Can the amount of reflection and transmission be controlled at an interface? |  |
| 5. How are reflection and transmission used in practical applications? |  |