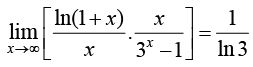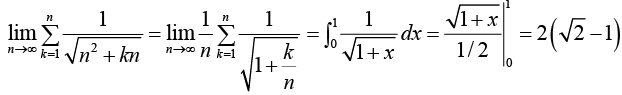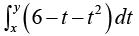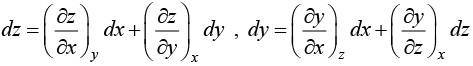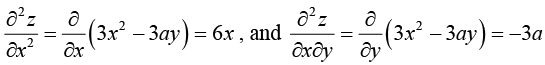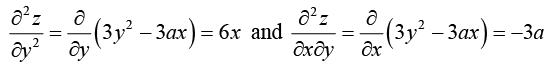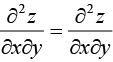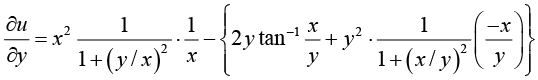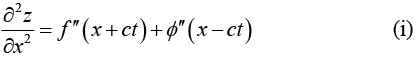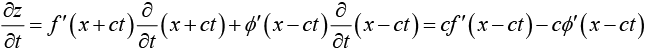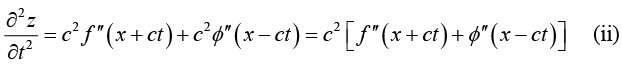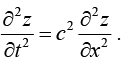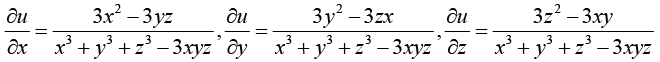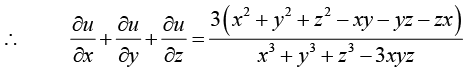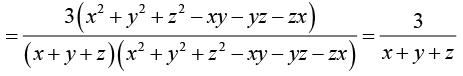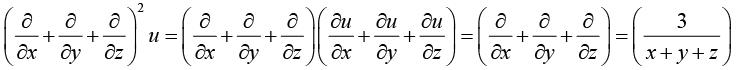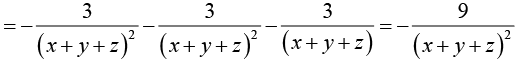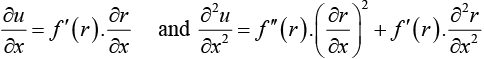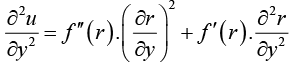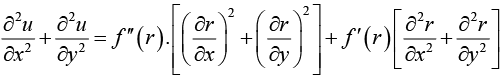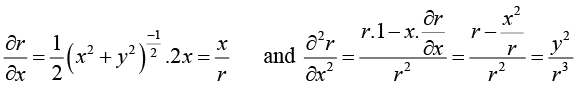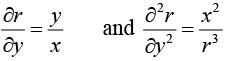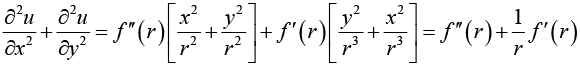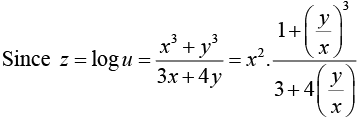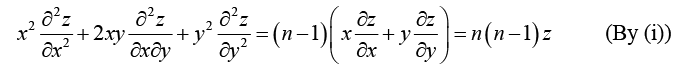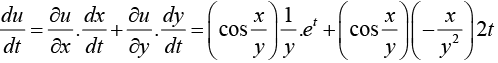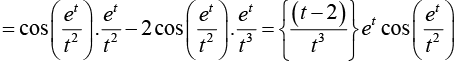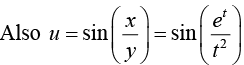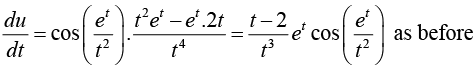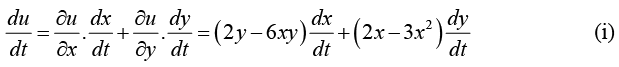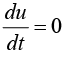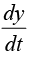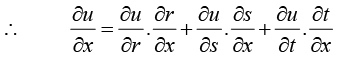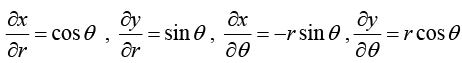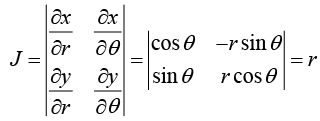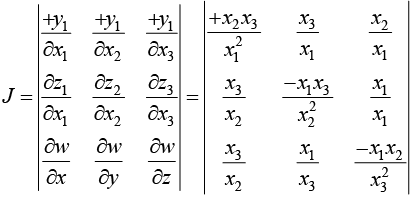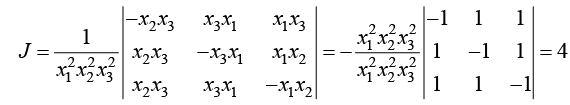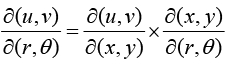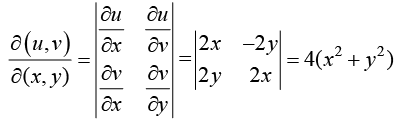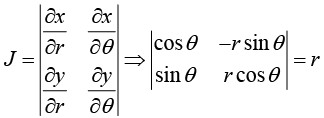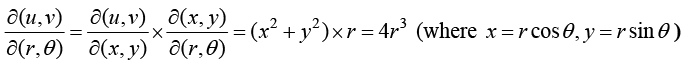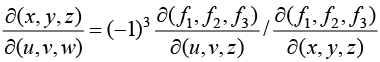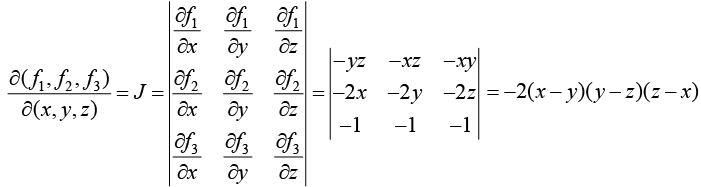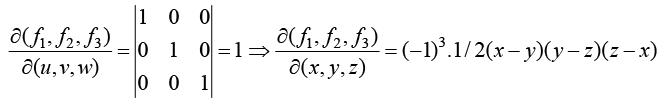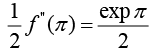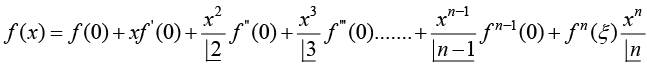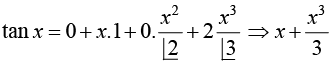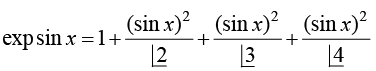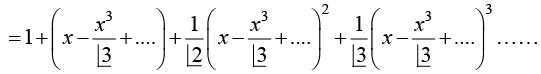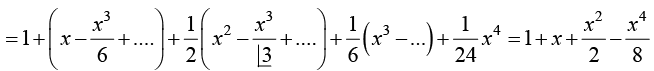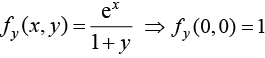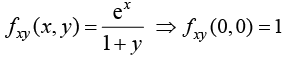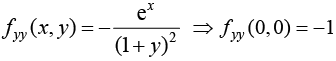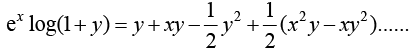Calculus of Single & Multiple Variables | Mathematical Methods - Physics PDF Download
| Table of contents |

|
| Limits |

|
| Continuity |

|
| Differentiability |

|
| Partial Differentiation |

|
| Jacobian |

|
| Taylor’s Series and Maclaurine Series Expansion |

|
Limits
The number A is said to be the limit of f (x) at x = a if for any arbitrary chosen positive
numbers, however small but not zero, there exists a corresponding number ε greater than zero such that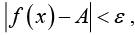 For all values of x for which 0
For all values of x for which 0 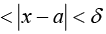
Right hand and Left hand Limit
If x approaches a from larger values of x than a, then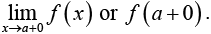
"Put a + h for x in f(x) and make h approaches zero'’. In short, we have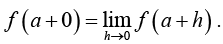
If x approaches a from smaller values of x than a, then 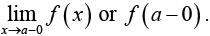 In this case
In this case
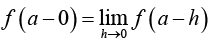
If both right hand and left hand limits of f(x), as x → a, exist and are equal in value, their common value, evidently, will be the limit of f(x), as x → a .
Theorem of Limits
If f (x) and g (x) are two functions then
1. 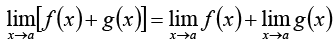
2. 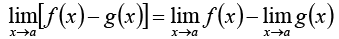
3. 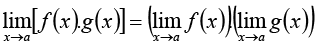
4. 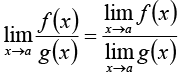
5. 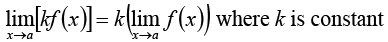
6. 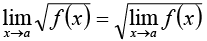
7. 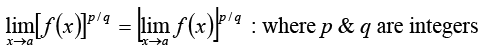
L’Hospital’s Rule
If a function f (x) takes the form 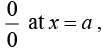 then we say that f (x) is indeterminate at x = a. If ∅(x) and ψ(x) are functions of x such that ∅(a) = 0 and ψ(a) = 0, then
then we say that f (x) is indeterminate at x = a. If ∅(x) and ψ(x) are functions of x such that ∅(a) = 0 and ψ(a) = 0, then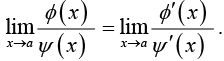
Some Important Standard Limits
1. 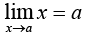
2. 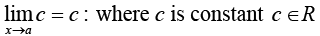
3. 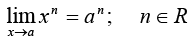
4. 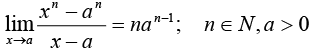
5. 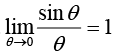
6. 
7. 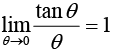
8. 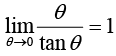
9. 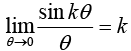
10. 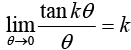
11. 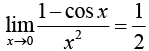
12. 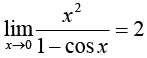
13. 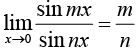
14. 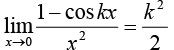
15. 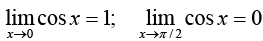
16. 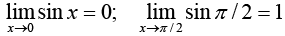
17. 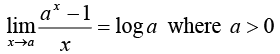
18. 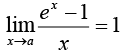
19. 
20. 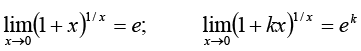
21. 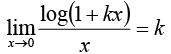
22. 
23. 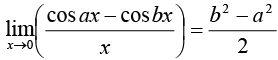
24. 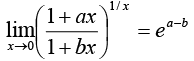
25. 
26. 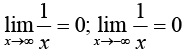
27. 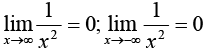
28. 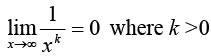
29. 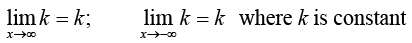
30. 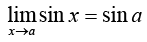
31. 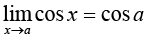
32.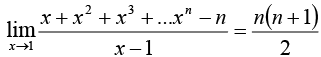
33. 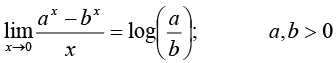
34. 
35. 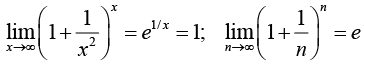
36. 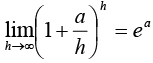
Example 1: Find the limit 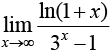
Example 2: Find the value of 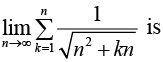
Continuity
f (x) is said to be continuous at x = a if R = L = V i.e.,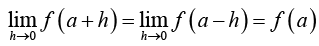
In case a function is not defined at x = a , i.e. f(a) does not exist or in case
theR.H.L ≠ L.H.L , then we say that the function is discontinuous at x = a. Its graph will show a break at x = a.
Example:
(i)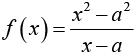 is discontinuous at x = a as f (a) does not exist.
is discontinuous at x = a as f (a) does not exist.
(ii)  is discontinuous at x = 0 because
is discontinuous at x = 0 because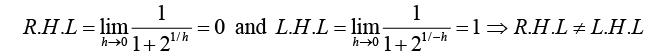
(iii) f (x) = 1 - cos e1x is discontinuous at x = 0 as f (0) = 1 - cos e1/0 is undefined. It is oscillating.
Example: Let the function f (x) be defined by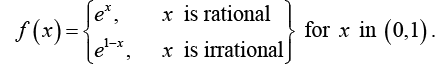
f(x) will be continuous at those points only where rational and irrational values coincide i.e. ex = e1 - x ⇒ ex = 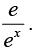 So /(x) is continuous at x = l/2 only.
So /(x) is continuous at x = l/2 only.
Differentiability
f (x) is said to be differentiable at x = a if R' = L' i.e,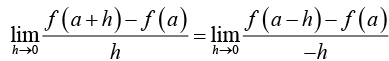
Example: f(x) = e-x2 is differentiable but g(x) =  is not differentiable.
is not differentiable.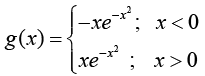
Right hand Limit 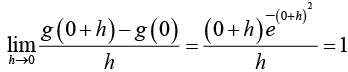
Left hand Limit 
Thus R' ≠ L' means g(x)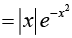 is not differentiable.
is not differentiable.
Tangents and Normal
Let y = f (x) be a given curve and P(x, y)and Q(x + δx, y + δy) be two neighbouring points on it. Equation of the line PQ is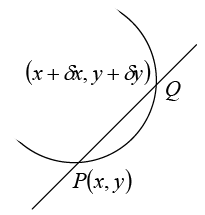
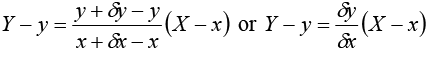
This line will be tangent to the given curve at P if Q → P which in tem means that δx → 0 and we know that lim 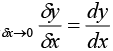
Therefore the equation of the tangent is Y - y = 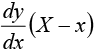
Normal at (x, y)
The normal at (x, v) being perpendicular to tangent will have its slope as 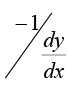 and hence its equation is Y - y =
and hence its equation is Y - y = 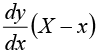
Geometrical meaning of dy/dx
dv/dx represents the slope of the tangent to the given curve y = f(x) at any point (x, y)
∴ 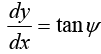 where ψ is the angle which the tangent to the curve makes with +ve
where ψ is the angle which the tangent to the curve makes with +ve
direction of x-axis.
In case we are to find the tangent at any point (x1, y1) then 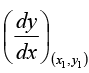 i.e. the value of
i.e. the value of 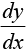 at (x1, y1) will represent the slope of the tangent and hence its equation in this case will be
at (x1, y1) will represent the slope of the tangent and hence its equation in this case will be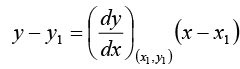
Normal 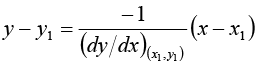
Condition for tangent to be parallel or perpendicular to x-axis
If tangent is parallel to x-axis or normal is perpendicular to x-axis then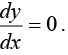
If tangent is perpendicular to x-axis or normal is parallel to x-axis then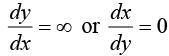
Maxima and Minima
For the function y = f (x) at the maximum as well as minimum point the tangent is parallel to x-axis so that its slope is zero.
Calculate  and solve for x. Suppose one root of
and solve for x. Suppose one root of 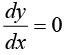 is at x = a .
is at x = a .
If 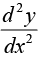 = negative for x = a, then maximum at x = a .
= negative for x = a, then maximum at x = a .
If 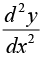 positive for x = a, then minimum at x = a .
positive for x = a, then minimum at x = a .
If 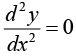 at x = a , then find
at x = a , then find 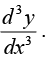
If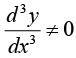 0 at x = a, neither maximum nor minimum at x = a.
0 at x = a, neither maximum nor minimum at x = a.
If 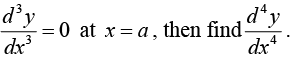
If 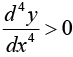 i.e., positive at x = a, then y is minimum at x = a and if
i.e., positive at x = a, then y is minimum at x = a and if 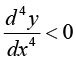 i.e -ve at
i.e -ve at
x = a , then y is maximum at x = a and so on.
Partial Differentiation
If a derivative of function of several independent variables be found with respect to any one of them, keeping the others as constants it is said to be partial derivative. The operation of finding the partial derivative of function of more than one independent variable is called partial differentiation.
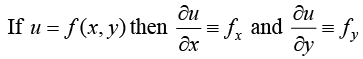
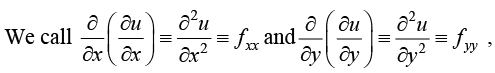
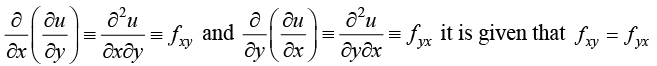
Euler Theorem of Homogeneous Function
If u is homogeneous function of x and y of degree n then 
For n variable function f = f(x1,x2,x3.........xn) of degree n then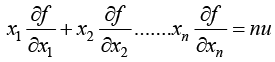
Total derivative u = f(x,y) x = ∅(t) and y = ψ(t) then 
Differentiation of implicit functions f(x, y) = c be an implicit relation between x and y which defines as a differential function of x then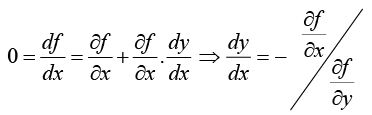
Change in variable u = f(x,y), x = ∅(s,t) and y = ∅(s,t)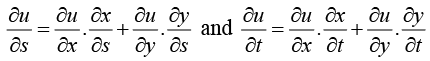
Maxima and Minima (of function of two independent variables)
Maximum Value of Function:
A function f (x,y) is said to have a maximum point (a,b), if these exists a neighbourhood N of (a,b) such that;
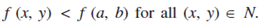
Minimum Value of Function:
A function f (x,y) is said to have a minimum point (a,b), if these exists a neighbourhood N of (a,b) such that;
Necessary and Sufficient Conditions for Maxima and Minima:
The necessary conditions for a functions f (x,y) to have either a maximum and minimum at a point (a,b) are fx (a,b) = 0 and fy (a,b) = 0. The point (x,y) where x and y satiesfy fx (x,y) = 0 and fy (x,y) = 0 are called the Stationary or the Critical value of the functions.
Suppose (a, b) is a critical value of the functions f (x,y). Then fx (a,b) = 0 and fy (a,b) = 0. Now denote:

1. Then. the functions f (x,y) has maximum at (a,b) if AC - B2 > 0 and A < 0.
2. The functions f (x,y) has minimum at (a,b) if AC - B2 > 0 and A > 0.
Maximum and Minimum value of functions are called the Extreme value of the function.
Working Rule to find the maximum and minimum value of function f (x,y):
1. Find fx (x,y) and fy (x,y).
2. Solve the equations fx (x,y) = 0 and fy (x,y) = 0.
3. Then find fxx (x,y), fxy (x,y) , fyy (x,y).
4. Then A = fxx (a,b) , B = fxy (a,b), C = fyy (a,b).
5. If AC - B2 > 0 and A < 0 the f has maximum at (a,b).
6. If AC - B2 > 0 and A > 0 the f has minimum at (a,b).
7. If AC - B2 < 0, then f has neither a maximum nor a minimum at (a,b) . The point (a,b) is called Saddle Point .
8. If AC - B2 = 0, further investigation is necessary.
Example 3: For what values of x and y , does the integral  dt attain its maximum?
dt attain its maximum?
l(x,y) or f(x,y) =
fx = -(6-x-x2) = x2+x-6 = (x + 3)(x-2), fy =6 - y - y2 = -(y + 3)(y - 2)
fx = 0 ⇒ x = 2,-3, fy = 0 ⇒ y = 2,-3so, stationary points are (2, 2),(2,-3),(-3,2)&(-3,-3)
fxx = 2x +1, fyy = -2y -1, fxy = 0
fxxfyy - (fxy)2 = - (2x +1) (2y +1)
At x = -3 and y = 2 and fxxfyy - (fxy)2 > 0
So maximum value of f (x, y) is obtained at x = -3 and y = 2
Example 4: If z = z(x, y) then prove that 
Example 5: Find the first and second partial derivatives of z = x3 + y3 - 3axy and prove that 
We have z = x3 + y3 - 3axy
Also
We observe that
Example 6: If u = x2 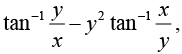
Show that 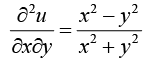 and
and 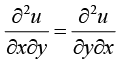
We have
∴Similarly,
and
Example 7: If z = f (x + ct) + ∅(x - ct), prove that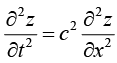
We have
and
Again
and
From (i) and (ii), it follows that
This is an important partial differential equation, known as wave equation.
Example 8: If u = log (x3 + y3 +z3 - 3xyz) , show that 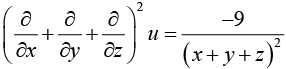
we have
Now
Example 9: If u = f (r) and x = r cos θ, y = r sin θ, prove that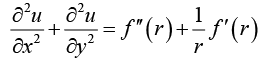
we have
Similarly,
∴
now to findetc,we write r = (x2 + v2)1/2
Similarly,
Substituting the values ofetc. in (i), we get
Example 10: Show that 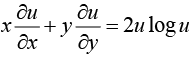 where
where 
∴ z is a homogeneous function of degree 2 in x and y .
By Euler’s theorem, we get
Hence (i) becomes
Example 11: If z is a homogeneous function of degree n in x and y , show that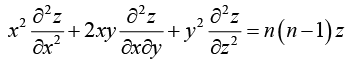
By Euler's theorem,
(i)
Differentiating (i) partially w.r.t. x, we get(ii)
Again differentiating (i) partially w.r.t. y , we get(iii)
Multiplying (ii) by x and (iii) by y and adding, we get
Example 12: Given u = sin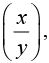 x = et and v = t2, find du/dt as a function of t. verify your dt result by direct substitution.
x = et and v = t2, find du/dt as a function of t. verify your dt result by direct substitution.
We have
∴
Example 13: If x increases at the rate of 2 cm /sec at the instant when x = 3 cm . and at what rate must y be changing in order that the function 2xy - 3x2y shall be neither increasing nor decreasing?
Let u = 2xy-3x2y, so that
when x = 3 and y = 1,
and u is neither increasing nor decreasing ,i.e.,
∴ (i) becomes 0 = (2-6x3)2 + (2x3-3x9)
orcm/sec. Thus y is decresing at the rate of 32/21 cm/sec.
Example 14: If μ = F(x-y,y -z,z- x) prove that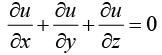
Put x-y = r,y-z = s and z-x = t, so that u = f (r,s,t) .
(i)
Similarly,(ii)
(iii)
Adding (i), (ii) and (iii), we get the required result.
Jacobian
If u and v are two function of two independent variable x and y then the determinant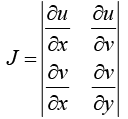
is called the Jacobian of u and v with respect to x and y which is written as 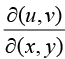 or
or
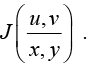
If u, v and w are functions of independent variable x, y and z then the determinant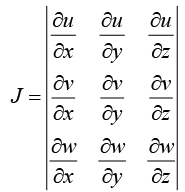
is called the Jacobian of u , v and w with respect to of x, y z which is written as 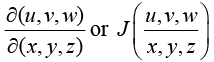
Properties of Jacobian
1. 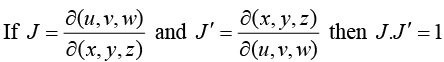
2. Chain rule for Jacobian if u,v arc function of r,s are function of x,y then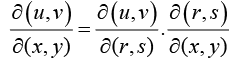
3. If u1, u2, u3 instead of being given explicitly in terms x1, x2, x3 be connected with them equations such as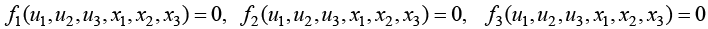
then 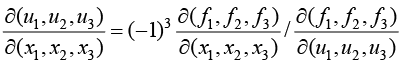
((-1)3 is for three variable system)
4. If u1, u2, u3 be functions of x1, x2, x3 then the necessary and sufficient condition for existence of a functional relationship of the form f1 (u1, u2, u3) = 0 is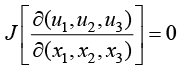
Example 15: In a polar coordinates x = r cos θ y = r cos θ then find
Example 16: 
Example 17: u = x2 - y2,v = 2xy x = rcosθ,y = rsinθ find
Use the formula
Example 18: u = xyz,v = x2 + y2 + z2,w = x + y + z find 
We are using property three
f1 = u - xyz, f2 = v - x2 - v2 - z2, f3 = w-x-y-z
Taylor’s Series and Maclaurine Series Expansion
If a function f(x) has continuous derivatives up to (n + 1)th order, then this function can be expanded in the following way:
where Rn called the remainder after (n + 1) terms, is given by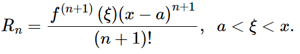
When this expansion converges over a certain range of x that is,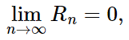 then the expansion is called Taylor Series of f(x) expanded about a.
then the expansion is called Taylor Series of f(x) expanded about a.
If a = 0, the series is called Maclaurin Series: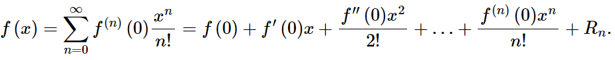
Maclaurine’s Development
Changing a to 0 and h to x one will get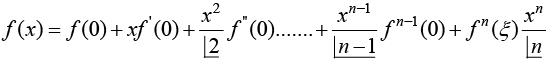
Where fn (ξ) is identified as reminder term ξ = θx and 0 < θ < 1
Example 19: In the Taylor series expansion of exp x + sin(x) about x = π then what is coefficient of (x - π)2.
Taylor series about x = π
f(x) = exp x + sin(x)
f(π) = exp π + sin(π) = exp π
f' (x) = exp x + cos x ⇒ f'(π) = exp π + cos π = exp π -1
f'' (x) = expx - sinx ⇒ f''(π) = expπ sinπ ⇒ f'' (π) = expπ
The coefficient of (x - π)2 is
Example 20: Expand Maclaurin's series expand of tan x up to x3
f(x) = tanx ⇒ f(0) = 0
f'(x) = sec2 x ⇒ f'(0) = 1f''(x) = 2 tan x sec2 x ⇒ f''(0) = 0
f''' (x) = 2sec2 x +6tan2 xsec2 x ⇒ f''' (0) = 2
Some Important Expansions
1. 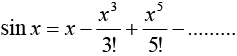
2.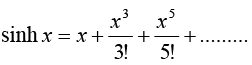
3.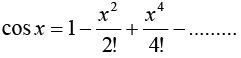
4.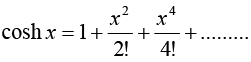
5.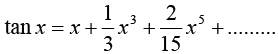
6.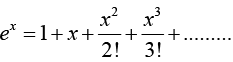
7.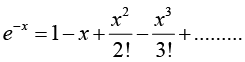
8.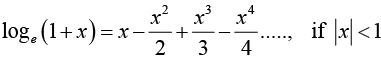
9. 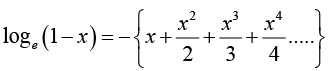
Example 21: Expand exp(sin x) by maclaurin series upto the term containing x4
Taylor 's theorem for function in two variable .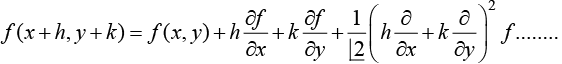
Puth h = x - a ,k = y - b
f(x, y) = f(a, b) + [(x - a)fx (a, b) + (y - b)fy (a, 6)]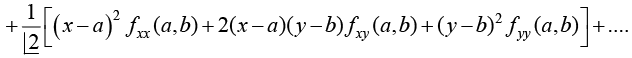
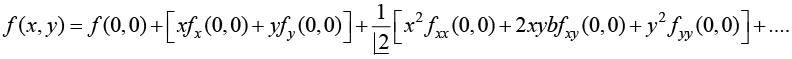
Example 22: Expand ex log(1 + y) upto powers of x and y upto term of two degree.
f (x, y) = ex log(1 + y) ⇒ f (0,0) = 0
fx(x, y) = ex log(1 + y) ⇒ fx (0,0) = 0,
fxx (x, y) = ex log(1+y) ⇒ fxx (0,0) = 0,
|
78 videos|18 docs|24 tests
|
FAQs on Calculus of Single & Multiple Variables - Mathematical Methods - Physics
| 1. What is the difference between limits and continuity in calculus? |  |
| 2. How do you find the partial derivatives of a multivariable function? |  |
| 3. What is the Jacobian and how is it used in calculus? |  |
| 4. How do you derive the Taylor series expansion of a function? |  |
| 5. What are the conditions for differentiability of a function at a point? |  |