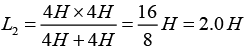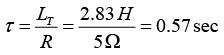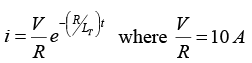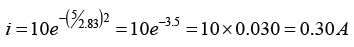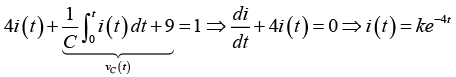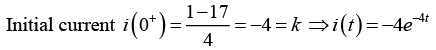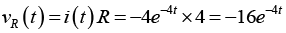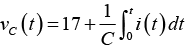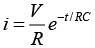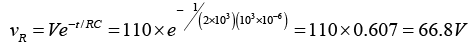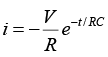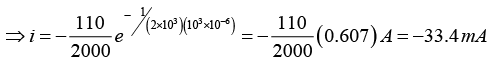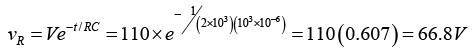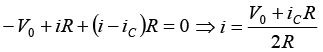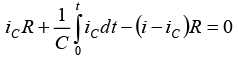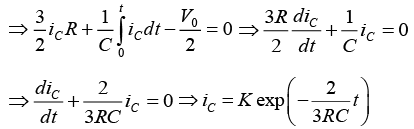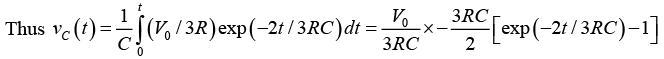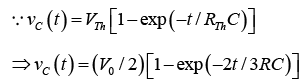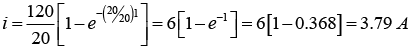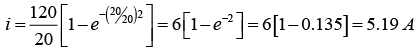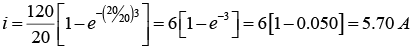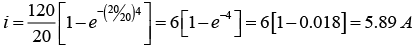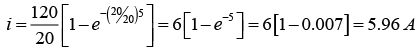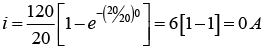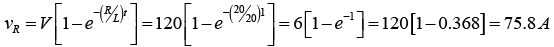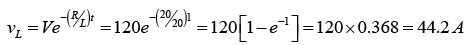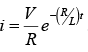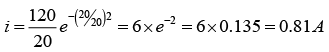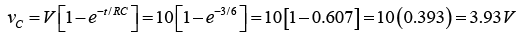DC Analysis of R, L, C Circuit: Assignment | Electricity & Magnetism - Physics PDF Download

Q.1. In the circuit shown in figure below find
(a)  the total inductance and
(b) the time constant of the circuit.
(c) Assume that a current of 10 A is flowing when the switch S is opened. Find the current 2 sec later.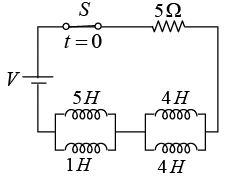

(a) Equivalent inductance of 5 H and 1 H in parallel:

Equivalent inductance of 4 H and 4 H in parallel:

Then total equivalent inductance of L₁ and L₂ in series:
L_T = L₁ + L₂ = 0.83 H + 2.0 H = 2.83 H

(b) the time constant of the circuit is the ratio of total inductance to the total resistance of 

the circuit

(c) Series RL current when the switch is opened

Q.2. The RC series circuit is shown in figure below. The capacitor is initially charged to 17V.  At time t = 0, the switch S is closed. Then in the transient state find
(a) current in the loop.
(b) voltage across resistor v_R (t).
(c) voltage across capacitor v_C (t).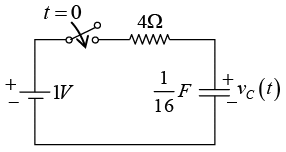

(a) Applying KVL,


(b) voltage across resistor
(c) voltage across capacitor

Q.3. A 1000μF capacitor and a 2kΩ resistor are connected in series across 110V dc source as shown in figure below.
(a) What is the current 1sec after the circuit is closed?

(b) What is the voltage across the resistor and capacitor at 1sec after the circuit is closed? 
(c) After the circuit has reached steady state when the capacitor has charged to 110 V, the switch is opened.
Find now
(i)  the current 1sec after the circuit is opened?
(ii)  the voltage across the resistor and capacitor at 1sec after the circuit is opened?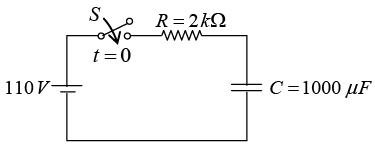

(a) As a series RC circuit when the switch is closed current
For t = 1sec:

(b) Voltage across the resistor at 1sec after the circuit is closed

Voltage across the capacitor at 1sec after the circuit is closed

As a check, substitute values for v_R and v_C in V = v_R+ v_C.
V = 66.8 + 43.2 = 110
(c)  (i)  As a series RC circuit when the switch is opened current
The current 1sec after the circuit is opened

(ii) Voltage across the resistor at 1sec after the circuit is opened

Voltage across the capacitor at 1sec after the circuit is opened

As a check, substitute values for v_R and v_C in V = v_R+ v_C .
V = -66.8 + 66.8 = 0V

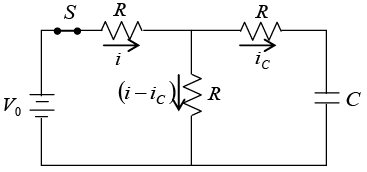
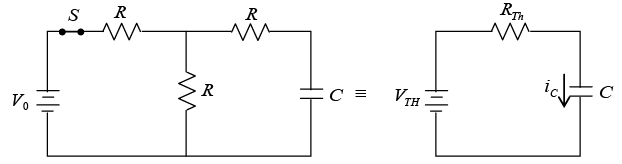
Q.4. A capacitor of 1000μF is connected to a battery of 2V through three equal resistors of 1kΩ and a switch S as shown below:
The capacitor is initially uncharged. At time t = 0, the switch S is closed. Find the voltage across capacitor as a function of time t for t > 0.

I^st Method:

Applying KVL in loop 1,

Applying KVL in loop 2,


Since at t = 0,


∵ V = 2V, R = 1kΩ and C = 1000μF
⇒ v_C(t) = (2/2) [1 - exp (-2t /3x10³ x10^-3)]
⇒ v_C(t) = [1 - exp(-2t/3)]

II^nd Method (Using Thevenins Equivalent Circuit)

where

Q.5. A 20H coil and a 20Ω resistor are connected in series across 120V dc source as shown in figure below.
(a) What is the current 1, 2, 3, 4 and 5 sec after the circuit is closed?
(b) What is the initial current at the instant circuit is closed?

(c) What is the voltage across the coil and across the resistor at 1sec after the circuit is closed?
(d) The switch is opened after having been closed for 7 sec . What is the value of current 2sec after the circuit is opened?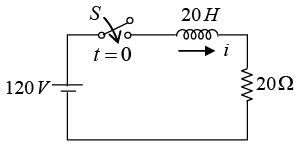

(a) Series RL current when the switch is closed
For t = 1sec:

For t = 2 sec:

For t = 3 sec:

For t = 4 sec:

For t = 5 sec:

(b) The initial current is that current when t = 0 sec , so

(c) Voltage across the resistor at 1sec after the circuit is closed

Voltage across the coil at 1sec after the circuit is closed

As a check, substitute values for v_R and v_L in V = v_R+ v_L.
V = 75.8 + 44.2 = 120
(d) Series RL current when the switch is opened

For t = 2 sec:

Q.6. For the circuit shown in figure, a 40μF capacitor is added across the 20μF capacitor. Find
(a) the time constant of the circuit.
(b) the voltage across the capacitor 3 sec after the capacitor starts charging.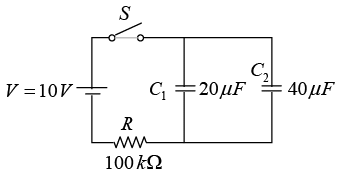

(a) The total equivalent capacitance of C₁ and C₂ in parallel:
C_T = C₁ + C₂ = 20 + 40 = 60μF
Then the time constant of the circuit is τ = RC_T = (100 x 10³) (60x10^-6) = 6.0 sec
(b) The voltage across the capacitor 3 sec after the capacitor starts charging is