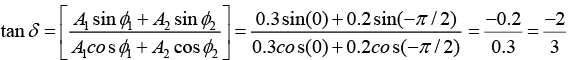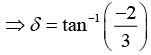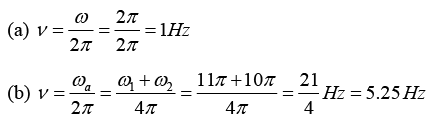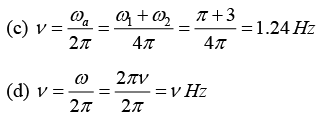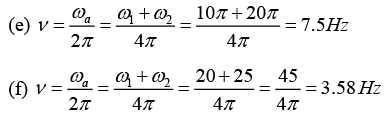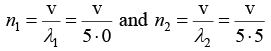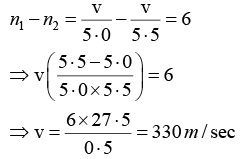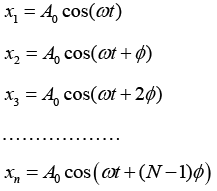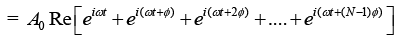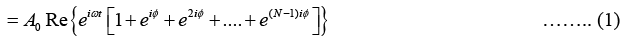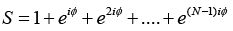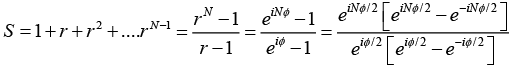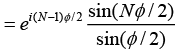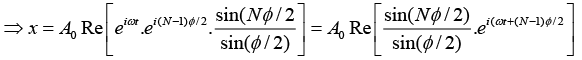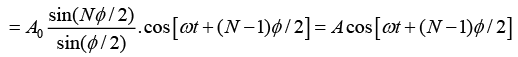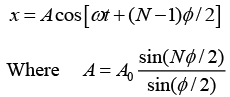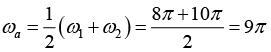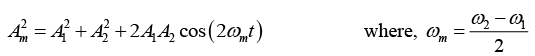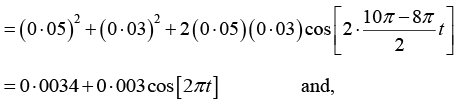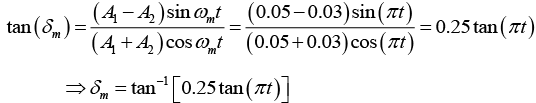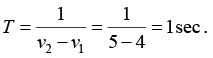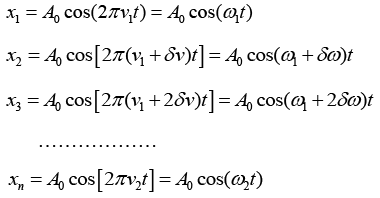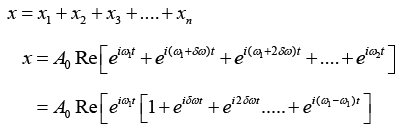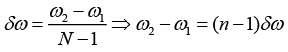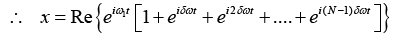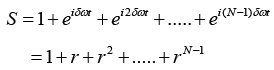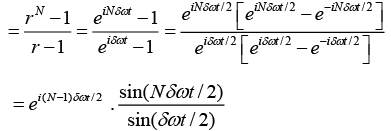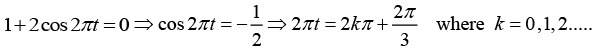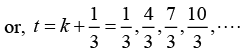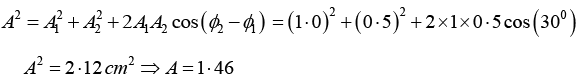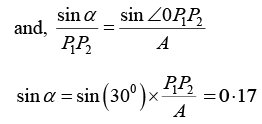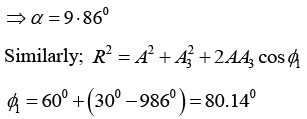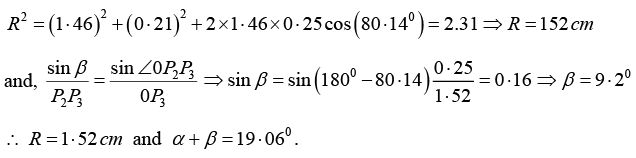Superposition of Harmonic Oscillations: Assignments | Oscillations, Waves & Optics - Physics PDF Download
Q.1. Two collinear simple harmonic motions, acting simultaneously on a particle are given by x1 = 0.3cos 2πt and x2 = 0.2sin(2πt). where x is expressed in cm and t in seconds. Write down the expressions for the resultant displacement as a function of time.
x = x1 + x2 = 0.3cos2πt + 0.2sin(2πt) = 0.3cos2πt + 0.2cos2πt-π/2 = x1+x2
x1 = 0.3cos 2πt and x1 = 0.2cos(2πt-π/2)
Compare it with the general equation
x1 = A1 cos(ωt+ϕ1) and x1 = A2 cos(ωt+ϕ2)
x = A cos(ωt + δ) = A cos(2π t + δ)
Where A2 = A12 + A22 + 2A1A2 cos(ϕ2 -ϕ1 )= (0.3)2 + (0.2)2 + 2(0.3)2(0.2) cos(-π/2)
⇒ A= 0.36
and
Q.2. A fork of unknown frequency gives 4 beats per second when sounded with another of frequency 256. The fork is now loaded with a piece of wax and again 4 beats per second are heard. Calculate the frequency of the unknown fork.
The frequency of one fork is 256 and it gives 4 beats per second with unknown tuning fork. Therefore, the frequency of the unknown fork must be 256 ± 4= 260 or 252.
When the unknown fork is loaded with wax, its frequency decreases. If its frequency is taken to be 252 , then on loading the frequency would decreases and so the number of beats it would give with the fork of frequency 256 must increase.
If the frequency of the unknown fork is taken to be 260 , then on loading it may decrease to 252 when it will again give 4 beats with the fork of frequency 256 . Hence the frequency of unknown fork before loading = 260
Q.3. Find the frequency of the combined motion of each of the following:
(a) sin (2πt - π/4) + cos (2πt)
(b) sin(10πt) + cos (11πt + π/4)
(c) cos(3t) - sin(πt)
(d) cos(2πvt) + b sin(2πvt + π/3)
(e) sin(20πt) + cos (10πt + π/4)
(f) 3 sin(25t) - 4 cos (20t - π/3)
The frequencies of the resultant motion for each case are
Q.4. Calculate the velocity of sound in a gas in which two waves of length 5.0 and 5.5 meter produce 6 beats per second.
Let v meter/sec be the velocity of sound. Then the frequencies of the two waves
will be
As the number of beats per second is 6 , we have
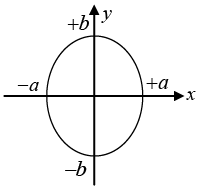
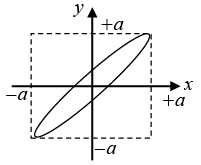
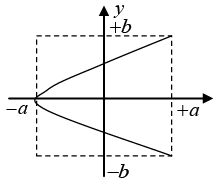
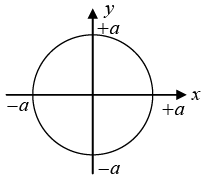
Q.5. Construct the Lissajous figures for the following motions:
(a) x = acosωt, y = bsinωt
(b) x = acos2ωt, y = acos [2ωt- (π / 4)]
(c) x = acos2ωt, y = bcosωt
(d) x = acos2ωt, y = asin 2ωt
(a)
x = a sin(ωt +π/2)t , y = b sin (ωt),
ω1 = ω2 , δ = π/2 and A1 ≠ A2 the resultant motion is ellipse
(b)
x = a cos 2ωt, y = a cos[(2ωt - π/4)]
ω1 = ω2, δ = π/2 and A1 ≠ A2
the resultant motion is oblique ellipse
(c)
x = acos2ωt, y= bcosωt
ω1 :ω2 = 2 :1 and δ = 0
(d)
x = a sin(2ωt +π/2) , y = a sin(2ωt)
Since, δ =π/2 and A1=A2
The resultant motion is circular
Q.6. A particle is subjected simultaneously to N simple harmonic motions of the same frequency. If the amplitude of each oscillation is A0 and ϕ is the phase difference between successive oscillations, show that amplitude of the resultant oscillation is given by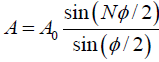
Consider N number of simple harmonic motions, each of amplitude A0 and successive phase difference of ϕ , whose displacements are written as
Resultant displacement of superposition of these N-number of SHM is written as
x = x1 + x2 + x3 + .... + xn
A0 cos(ωt) + cos(ωt +ϕ) + cos(ωt + 2ϕ) + ..... + cos(ωt+(N -1)ϕ)]
This can be written in a complex form
Let us introduce a new variable,
and also put r =eiϕ in above equation, we get
The resultant displacement becomes
Q.7. A sound wave of unknown frequency gives 10 beats with a wave of frequency 300 Hz and 15 beats with a wave of frequency 325 Hz. What is the frequency of the unknown wave?
The number of beats per second is equal to the difference frequency of the two waves. Then, if n is the frequency of the unknown wave, we have
n = 300 ± 10 = 310, 290 and, n = 325 ± 15 = 340, 310.
Obviously, the frequency of the unknown wave is 310 Hz .
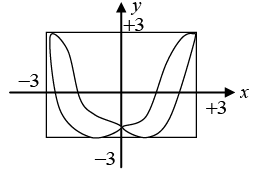
Q.8. Two vibrations, at right angle to each other, are described by the equations
x=3cos4πt and y = 3cos (8πt + π/3). where x and y are expressed in centimeters and t in seconds. Construct the Lissajous figure of the combined motion.
Since, ω2 = 2ω1, δ=π/3
Q.9. Two vibrations along the same line are described by the equations
x1 = 0.05cos 8πt and x2 = 0.03cos10πt where x is expressed in meters and t in seconds. Obtain the equation describing the resultant motion and hence find the beat period.
The equation of the resultant displacement is
x= x1 + x2 = 0.05cos(8πt)+ 0.03cos(10πt)
Compare it with the general equation
x = A1cos(ω1t) + A2cos (ω2t)
x = Amcos (ωat + δm)
where
Beat period is
Q.10. A tuning fork of unknown frequency gives 5 beats when sounded with another tuning fork frequency 384 Hz . When the other fork is loaded with a little wax, only 3 beats are heard. Calculate the frequency of the fork.
The forks produce 5 beats in 1 second. Hence the difference between their frequencies is 5. As the frequency of the second fork is 384, that of the first should be 384 ± 5= 389 or 379.
When the prong of the second fork is loaded, its frequency decreases slightly. But now the beat – frequency of the first fork must be less than 384 that is 379.
Q.11. A particle is subjected simultaneously to N simple harmonic oscillations having
frequencies distributed uniformly between v1 and v2. If the amplitude of each oscillations is A0, initial phase of each is zero and δv is the frequency difference between successive components, show that the resultant displacement of the particle is given by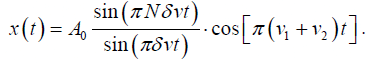
The displacement equation of N number of simple harmonic oscillations of having frequencies distributed uniformly between v1 and v2. If the amplitude of each oscillations is A0, initial phase of each is zero and δv is the frequency difference between successive components can be written as
The equation of the resultant displacement is written as
Where,
let
where r =eiδωt
Q.12. Calculate the number of beats heard per second if there are three sources of sound of frequencies 400, 401 and 402 of equal intensities sounded together.
Let a be the amplitude, and ( n - 1)n, and (n + 1) the frequencies of the three waves. The equation for the resultant displacement is
y = a sin 2π(n -1)t + asin2πnt + asin 2π (n+1)t
Adding the first and the third terms, we getv = a sin 2πnt+ 2asin(2πnt)cos2πi = a sin 2πt(1+ 2cos2πt)
= a(1+ 2cos2πt)sin2πnt
This shows that the resultant amplitude is a (1+2cos 2πt). It is a maximum when
cos2πt = +1 ⇒ 2p t = 2kp ⇒ t =k where k = 0,1, 2, 3.....
∴ Amplitude maxima occur at intervals of 1 second. Similarly, the resultant amplitude is minimum
when,
∴ Amplitude minima also occur at intervals of 1 second. Thus, the resultant sound passes through one maximum and one minimum in each second. In other words, the number of beats per second is one.
Q.13. Two vibrations, at right angle to each other, are described by the equations x=3cos5πt and y = 2cos(5πt + π/3). where x and y are expressed in centimeters and t in seconds. Construct the curve for the combined motion.
Since, ω1 = ω2, δ = π/3 and A1 ≠A2, the resultant motion is oblique ellipse
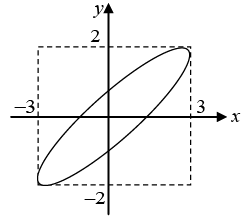
Q.14. A particle is simultaneously subjected to three simple harmonic motions, all of the same frequency and in the same direction. If the amplitudes are 1.0cm, 0.5cm, 0.25cm respectively and the phase of the second relative to the first is 30° and that of the third relative to the second is 60°, find the amplitude of the resultant displacement and its phase relative to the first component.
|
54 videos|22 docs|14 tests
|
FAQs on Superposition of Harmonic Oscillations: Assignments - Oscillations, Waves & Optics - Physics
| 1. What is superposition of harmonic oscillations? |  |
| 2. How does the superposition principle apply to harmonic oscillations? |  |
| 3. Can the superposition of harmonic oscillations lead to destructive interference? |  |
| 4. How is the principle of superposition applied in analyzing complex harmonic oscillations? |  |
| 5. What are some practical applications of the superposition of harmonic oscillations? |  |