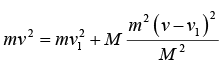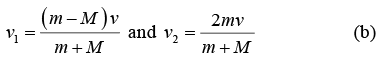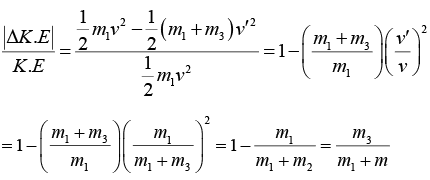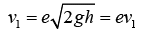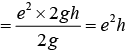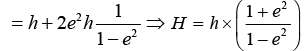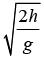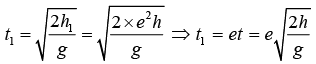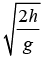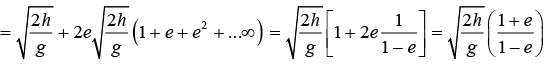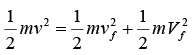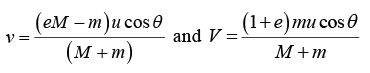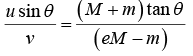Conservation of Momentum & Collision | Mechanics & General Properties of Matter - Physics PDF Download
In the last section we found that the total external force F acting on a system is related to the total momentum P of the system by F = dP/dt
Consider the implications of this for an isolated system, that is, a system which does not interact with its surroundings. In this case F = 0 , and dP/dt = 0 . The total momentum is constant; no matter how strong the interactions among an isolated system of particles, and no matter how complicated the motions, the total momentum of an isolated system is constant. This is the law of conservation of momentum. As we shall show, this apparently simple law can provide powerful insights into complicated systems.
Collisions
Contrary to the meaning of the term 'collision' in our everyday life in Physics it does not necessarily mean one particle 'striking' against other. Indeed two particles may not even touch each other and may still be said to collide. All that is implied is that as the particles approach each other.
(i) An impulse (a large for a relatively short time) acts on each colliding particles.
(ii) the total momentum of the particles remain conserved. The collision is in fact a redistribution of total momentum of the particles. Thus, law of conservation of linear momentum is indispensible in dealing with the phenomenon of collision between particles. Consider a situation shown in figure. Two blocks of masses m1 and m2 are moving with velocities v1 and v2 (<v1) along the same straight line in a smooth horizontal surface. A spring is attached to the block of mass m2. Now, let us see what happens during the collision between two particles. Figure (a) Block of mass m1 is behind m2 since v1 > v2 , the blocks will collide after some time.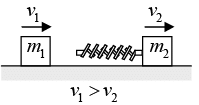 Figure (b) The spring is compressed. The spring force F (= kx) acts on the two blocks in the directions shown in figure. This force decreases the velocity of m1 and increases the velocity of m2.
Figure (b) The spring is compressed. The spring force F (= kx) acts on the two blocks in the directions shown in figure. This force decreases the velocity of m1 and increases the velocity of m2.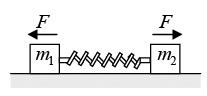 Figure (c) The spring will compress till velocity of both the blocks become equal. So, at maximum compression (say xm) velocities of both the blocks are equal (say v)
Figure (c) The spring will compress till velocity of both the blocks become equal. So, at maximum compression (say xm) velocities of both the blocks are equal (say v)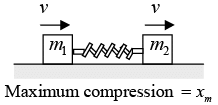 Figure (d) Spring force is still in the directions shown in figure, i.e., velocity of block m1 is further decreased and that of m2 is increased. The spring now starts relaxing.
Figure (d) Spring force is still in the directions shown in figure, i.e., velocity of block m1 is further decreased and that of m2 is increased. The spring now starts relaxing.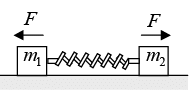 Figure (e) The two blocks are separated from one another. Velocity of block m2 becomes more than the velocity of b lock m1, i.e.
Figure (e) The two blocks are separated from one another. Velocity of block m2 becomes more than the velocity of b lock m1, i.e.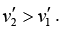
Line of Impact
The line passing through the common normal to the surfaces in contact during impact is called line of impact. The force during collision acts along this line on both the bodies.
Direction of Line of impact can be determined by
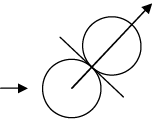 (a) Geometry of colliding objects like spheres, discs, wedge etc.
(a) Geometry of colliding objects like spheres, discs, wedge etc.
(b) Direction of change of momentum.
If one particle is stationary before the collision, then the line of impact will be along its motion after collision.
Classification of Collisions
(A) Head-on collision: If the velocities of the particles are along the same line before and after the collision, (i) Elastic collision: In an elastic collision, the particle regain their shape and size completely after collision. i.e., no fraction of mechanical energy remains stored as deformation potential energy in the bodies. Thus, kinetic energy of system after collision is equal to kinetic energy of system before collision. Thus, in addition to the linear momentum, kinetic energy also remains conserved before and after collision.
(i) Elastic collision: In an elastic collision, the particle regain their shape and size completely after collision. i.e., no fraction of mechanical energy remains stored as deformation potential energy in the bodies. Thus, kinetic energy of system after collision is equal to kinetic energy of system before collision. Thus, in addition to the linear momentum, kinetic energy also remains conserved before and after collision.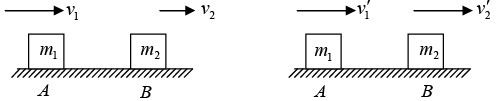
Consider two elastic bodies A and B moving along the same line (figure). The body A has a mass m1 and moves with a velocity v1 towards right and the body B has a mass m2 and moves with a velocity v2 in the same direction. We assume v1 > v2 so that the two bodies may collide.
Let v'1 and v'2 be the final velocities of the bodies after the collision. The total linear momentum of the two bodies remains constant, so that,
m1v1 + m2v2 = m1v'1 + m2v'2 (i)
or m1v1 - m1v'1 = m2v'2 - m2v2
or m1(v1 - v'1) = m2(v'2 - v2) (ii)
Also, since the collision is elastic, the kinetic energy before the collision is equal to the kinetic energy after the collision. Hence,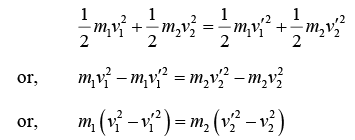 (iii)
(iii)
Dividing (iii) by (ii)
v1 + v'1 = v'2 + v2
v1 - v2 = v'2 - v'1 (iv)
is the rate at which the separation between the bodies decreases before the collision. Similarly, (v'2 - v'1) is the rate of increase of separation after the collision. So the equation (iv) may be written as
Velocity of separation (after collision) = Velocity of approach (before collision)...
This result is very useful in solving problems involving elastic collision. The final velocities v'1 and v'2 may be obtained from equation (i) and (iv). Multiply equation (iv) by m2 and subtract from equation (i).
or 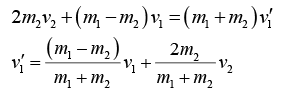 (A)
(A)
Now multiply equation (iv) by m1 and add to equation (i),
2m1v1 - (m1 - m2)v2 = (m2 + m1)v'2
or 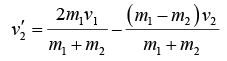 (B)
(B)
Equations, (A) and (B) give the final velocities in terms of the initial velocities and the masses.
For inelastic collision velocities after collision are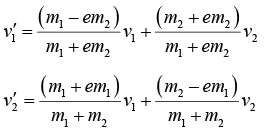
Special Cases
(a) Elastic collision between a heavy body and a light body: Let m1 >> m2. A heavy body hits a light body from behind.
We have, 
With these approximations the final velocities of the bodies are, from (A) and (B),
v'1 ≈ v1 and v'2 ≈ 2v1 - v2.
The heavier body continues to move with almost the same velocity, If the lighter body were kept at rest v2 = 0, v'2 = 2v1 which means the lighter body, after getting a push from the heavier body will fly away with a velocity double the velocity of the heavier body.
Next, suppose m2 >> m1. A light body hits a heavy body from behind.
We have,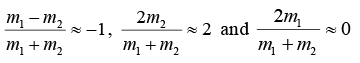
The final velocities of the bodies are, from (A) and (B), v'1 ≈ -v1 + 2v2 and v'2 ≈ v2
The heavier body continues to move with almost the same velocity, the velocity of the lighter body changes. If the heavier body were at rest, v2 = 0 then v'1 = -v1 the lighter body returns alter collision with almost the same speed. This is the case when a ball collides elastically with a fixed wall and returns with the same speed.
(b) Elastic collision of two bodies of equal mass
Putting m1 =m2 in equation (A) and (B) v'1= v2 and v'2 = v1.
When two bodies of equal mass collide elastically, their velocities are mutually interchanged.
Theorem: In a 1-D elastic collision, the relative velocity of the two particles after the collision is the negative of the relative velocity before the collision.
Proof: Let the masses be m and M . Let vi and Vi be the initial velocities, and let vf and Vf be the final velocities. Conservation of momentum and energy give
mvi = Mvi = mvf + MVf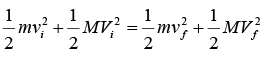 (A)
(A)
Rearranging these yields
m(vi - vf) = M(Vf - Vi)
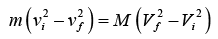 (B)
(B)
Dividing the second equation by the first gives vi + vf = Vi + Vf. Therefore,
vi - Vi = -(vf - Vf)
as we wanted to show. In taking the quotient of these two equations, we have lost the vf = vi and Vf = Vi solution. But as stated in the above example, this is the trivial solution.
This is a splendid theorem. It has the quadratic energy-conservation statement built into it. Hence, using this theorem along with momentum conservation (both of which are linear equations and thus easy to deal with) gives the same information as the standard combination of Eqs. (A). Another quick proof is the following. It is fairly easy to see that the theorem is true in the CM frame, so it is therefore true in any frame, because it involves only differences in velocities.
Example 12: (Two masses in 1-D, again): A mass m with speed v approaches a stationary mass M as given in figure below. The masses bounce off each other elastically. What are the final velocities of the particles? Assume that the motion takes place in 1-D.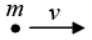
Let v1 and v2 be the final velocities of the masses. Then conservation of momentum and energy give, respectively,
mv + 0 = mv1 + Mv2(a)
We must solve these two equations for the two unknowns v1 and v2. Solving for v2 in the first equation and substituting into the second gives
⇒ 0 = (m +M) v12 - 2mvv1 + (m - M)v2⇒ 0 = ((m + M)v1 (m - M) v)(v1 - v)
One solution is v1 = v, but this isn’t the one we’re concerned with. It is of course a solution, because the initial conditions certainly satisfy conservation of energy and momentum with the initial condition (a fine tautology indeed). If you want, you can view v1 = v as the solution where the particles miss each other. The fact that v1 = v is always a root can often save you a lot of quadratic-formula trouble.
The v1 = v(m - M)/(m + M) root is the one we want. Plugging this v1 back into the first of equation (a) to obtain v2 gives
This solution was somewhat of a pain, because it involved a quadratic equation. The following theorem is extremely useful because it offers a way to avoid the hassle of quadratic equations when dealing with 1-D elastic collisions.
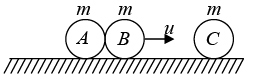
Example 13: Three balls A,B and C of same mass ‘m’ are placed on a frictionless horizontal plane in a straight line as shown. Ball A is moved with velocity u towards the middle ball B . If all the collisions are elastic then, find the final velocities of all the balls.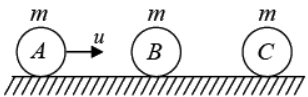
A collides elastically with B and comes to rest but B starts moving with velocity u
After a white B collides elastically with C and comes to rest but C starts moving with velocity u .
∴ Final velocities VA = 0; VB = 0 and VC = u
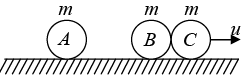
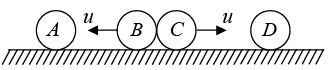
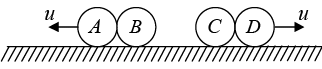
Example 14: Four identical balls A,B, C and D are placed in a line on a frictionless horizontal surface. A and D are moved with same speed ‘ u ’ towards the middle as shown. Assuming elastic collisions, find the final velocities.
A and D collides elastically with B and C respectively and come to rest but B and C starts moving with velocity u towards each other as shown.
B and C collides elastically and exchange their velocities to move in opposite, directions
Now; B and C collides elastically with A and D respectively and come to rest but A and D starts moving with velocity u away from each other as shown
∴ Final velocities VA = u(⇠): VB = 0; VC = 0 and VD = u(⇢)
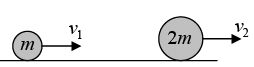
Example 15: Two particles of mass m and 2m moving in opposite directions Collide elastically with velocity v and 2v respectively. Find their velocities after collision.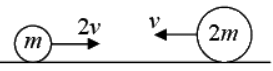
Let the final velocities of m and 2m be v1 and v2 respectively as shown in the figure By conservation of momentum:
m(2v) +2m (-v) = m(v1) + 2m(v1) or 0 = mv1 + 2mv2
or v1 + 2v2 = 0 (i)
and since the collision is elastic:
v2 - v1 = 2v(-v) or v2 - v1 = 3v (ii)
Solving the above two equations, we get,v2 = v and v1 = -2v
i.e., the mass 2m returns with velocity v while the mass m returns with velocity 2v in the direction in the figure:
(ii) Inelastic collision: In an inelastic collision, the particle do not regain their shape and size completely after collision. Some fraction of mechanical energy is retained by the colliding particles in the form of deformation potential energy. Thus, the kinetic energy of the particles no longer remains conserved. However, in the absence of external forces, law of conservation of linear momentum still holds good. Practically most of the collisions are inelastic.
Example 16: A block m1 strikes a stationary block m3 perfectly inelastically in a head on collision. Another block m2 is kept on m3 Neglecting the friction between all contacting surfaces. Find the fractional decrease of K.E of the system in collision.
Since the impact between m1 and m3, is inelastic, m1, and m3, will move together towards right but m2 does not move due to the absence of friction.
The velocity of the combined mass,
(iii) Perfectly inelastic or perfectly plastic (e = 0): If velocity of separation just after collision becomes zero then the collision is perfectly inelastic. Collision is said to be perfectly inelastic if both the particles stick together after collision and move with same velocity,
Note: Actually, collision between all real objects are neither perfectly elastic nor perfectly inelastic, its inelastic in nature.
Perfectly Inelastic Collision in One Dimension
Final Velocity
When perfectly inelastic bodies moving along the same line collide, they stick to each other. Let m1 and m2 be the masses, v1 and v2 be their velocities before the collision and v be the common velocity of the bodies after the collision. By the conservation of linear momentum,
m1v1 +m2v2 = m1v + m2v
or 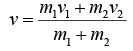
Coefficient of Restitution (e)
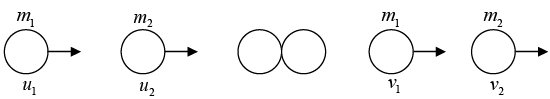
When 2 masses m1 and m2 collide there is deformation of the mass. As collision is not elastic and the masses try to regain their shapes, some energy is lost as bodies are not perfectly elastic. Therefore reducing their velocities. For perfectly elastic bodies, absence of friction leads to conservation of energy and bodies regain their shapes. This coefficient is defined as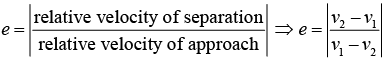
e is usually a positive, real number between 0 and 1:
e = 0 : This is a perfectly inelastic collision. This means kinetic energy along the common normal is 0. Kinetic energy is converted to heat or work done in deforming the objects.
0 < e<1 : This is a real-world inelastic collision, in which some kinetic energy is dissipated.
e = 1 : This is a perfectly elastic collision, in which no kinetic energy is dissipated, and the objects rebound from one another with the same relative speed with which they approached.
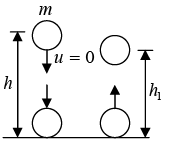
Example 17: A ball of mass m strikes a surface falling freely from height h . The coefficient of restitution between ball and surface is e.
(a) Find the total distance before it stops.
(b) Find the total time elapsed before it stops.
(a) Velocity of ball just before striking surface
A ball of mass m strikes a surface falling freely from height h. The coefficient of restitution between ball and surface is e. Velocity of ball just before striking surface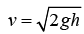
The velocity with which ball rises
It goes to a height h1
as 0 = (ev)2 - 2gh1 ⇒ h1
After second rebound, velocity v2 = ev1 = e2v and it goes to a height h2 = e2h1 = e4h
After nth rebound hn = e2nh and vn = env
Total distance moved by ball till it stops
H = h + 2h1 + 2h2 + ...∞ terms = h + 2(e2h + e4h +....∞ terms)
= h + 2e2(1 + e2 + ...∞ terms)for an infinite G.P.)
(b) Time taken by the ball to reach the ground from height h,t =
For 1st rebound,
Similarly, for 2nd rebound t2 = e + 1 = e2
Total time taken by ball before stopping
T = t + (2t1 + 2t2 + ....∞ terms)
For e = 1, collision is perfectly plastic,(ball does not bounce after rebound)
for e = 1, T ⇢ ∞, ball keeps on bouncing to same height indefinitely as no energy is lost.
Two-Dimensional Motion
Oblique Collision:
Let’s now look at the more general case of two-dimensional motion. Three-Dimensional motion is just more of the same, so we’ll confine ourselves to 2-D. Everything is basically the same as in 1-D, except that there is one more momentum equation, and one more variable to solve for. This is best seen through an example.
Elastic Collision in Two Dimensions
Consider two objects A and B of mass m1 and m2 kept on the X - axis (figure). Initially, the object B is at rest and A moves towards B with a speed u1. If the collision is not head -on (the force during the collision is not along the initial velocity), the objects move along different lines. Suppose the object A moves with a velocity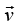 making an angle θ with the X - axis and the object B moves with a velocity
making an angle θ with the X - axis and the object B moves with a velocity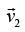 making an angle θ with the same axis. Also, suppose
making an angle θ with the same axis. Also, suppose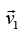 and
and 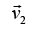 lie in X - Y plane. Using conservation of momentum in X and Y directions, we get
lie in X - Y plane. Using conservation of momentum in X and Y directions, we get
m1u1 = m1v1 cosθ + m2v2 cos∅ (i)
and 0 = m1v1sinθ - m2v2 sin∅ (ii)
If the collision is elastic, the final kinetic energy is equal to the initial kinetic energy. Thus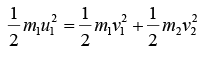 (iii)
(iii)
We have four unknowns v1,v2,θ and ∅ to describe the final motion whereas there are only three relations. Thus, the final motion cannot be uniquely determined with this information.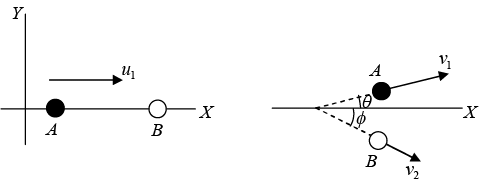
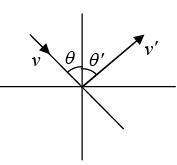
Example 18: A billiard ball with speed v approaches an identical stationary one. The balls bounce off each other elastically, in such a way that the incoming one gets deflected by an angle θ (see figure). What are the final speeds of the balls?
What is the angle ∅ at which the stationary ball is deflected?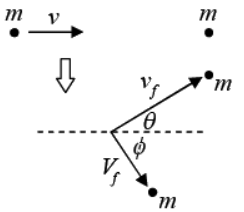
Let vf and Vf be the final speeds of the balls. Then conservation of px, py, and E give, respectively.
mv = mvf + cos θ + mVf cos ∅
0 = mvf sin θ - MVf sin ∅
We must solve these three equations for the three unknowns vf,Vf, and ∅. There are various ways to do this. Here’s one. Eliminate ∅ by adding the squares of the first two equations (after putting the vf terms on the left-hand side) to obtain v2 - 2vvf cos θ + v2f = V2f .
Now eliminate Vf by combining this the third equation to obtain vf = v cosθ
The third equation then yields Vf = vsinθ
The second equation then gives m (v cosθ) sinθ = m(v sinθ) sin∅; which implies cos θ = sin∅ (or θ = 0, which corresponds to no collision). Therefore, ∅ = 900 - θ
In other words, the balls bounce off at right angles with respect to each other. This fact is well known to pool players. Problem 5.19 gives another (cleaner) way to demonstrate this result. Note that we needed to specify one of the four quantities, vf,Vf,θ,∅. (we chose θ), because we have only three equations. Intuitively, we can’t expect to solve for all four of these quantities, because we can imagine one ball hitting the other at various distances away from directly head-on, which will cause the balls to be deflected at various angles.
Example 19: Two smooth spheres A and B , or equal radius but masses m and M , are free to move on a horizontal table A is projected with speed u towards B which is at rest. On impact, the line joining their centres is inclined at an angle θ to the velocity of A before impact. if e is the coefficient of restitution between the spheres, find the speed with which B begins to move. If A ’s path after impact is perpendicular to its path before impact, show that tan2θ = eM - m/M + m.
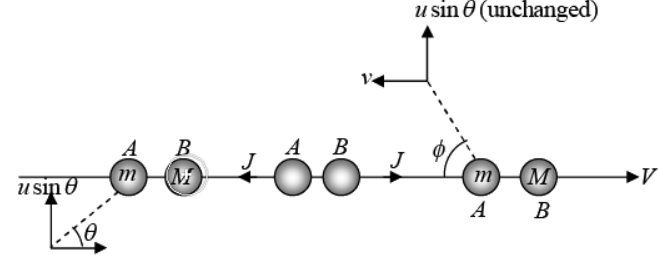
When B is struck by the impulse J, it begins to move in the direction of J as shown in the diagram. Along the line of centre, we apply
(a) Conservation of linear momentum,
i.e., mu cosθ = MV - mv (i)
(b) Law of restitution,
i.e., eu cosθ = V + v (ii)
Solving equations, (i) and (ii), we get
Hence, tanθ =
Example 20: A ball of mass m hits a floor with a speed v making an angle of incidence θ with the normal. The coefficient of restitution is e.
(a) Find the speed of the reflected ball.
(b) Find the angle of reflection of the ball.
(c) Find the angle of reflection for elastic collision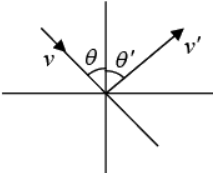
(a) Suppose the angle of reflection is θ' and the speed after the collision is v'. The floor exerts a force on the ball along the normal during the collision. There is no force parallel to the surface. Thus, the parallel component of the velocity of the ball remains unchanged. This gives
v'sinθ' = v sin θ (i)
For the components normal to the floor,
The velocity of separation = v' cosθ'
and the velocity of approach = v cosθ
Hence, v' cosθ' = ev cosθ (ii)
From (i) and (ii),
(b) Dividing equation (i) and (ii), we get tan θ' = tan θ/e(c) For elastic collision, e = 1 so that θ' = θ and v' = v
Note: If collision is perfectly elastic, no energy is absorbed by the floor and hence e = 1 So tanθ = tanθ' ⇒ θ = θ' and v' = v
Impulse:
Example 21: A small ball of mass m collides with a rough wall having coefficient of friction µ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e then find the reflected velocity v of the ball just after collision.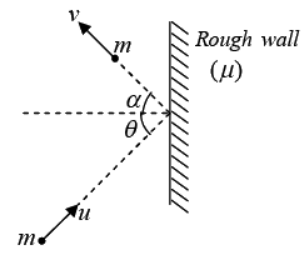
mv cos cosα - (m(-u cosθ)) = ∫Ndt
mv sin α - mu sin θ = - μ∫Ndt
andv cos α = eu cos θ
or (mv sinα - mu sinθ = -µ(mv cosα + mu cosθ)
or v = u/sin α [sin θ - μ cos θ(e + 1)]
|
61 videos|23 docs|25 tests
|
FAQs on Conservation of Momentum & Collision - Mechanics & General Properties of Matter - Physics
| 1. What is a perfectly inelastic collision in one dimension? |  |
| 2. How is momentum conserved in a perfectly inelastic collision in one dimension? |  |
| 3. What happens to the kinetic energy in a perfectly inelastic collision in one dimension? |  |
| 4. How can the final velocity of the combined object be calculated in a perfectly inelastic collision in one dimension? |  |
| 5. Can a perfectly inelastic collision in one dimension have a negative final velocity? |  |