Linear Algebra: Matrices - Assignment | Mathematical Methods - Physics PDF Download
Q.1. If θ - ∅ = an odd multiple of — find the product of matrices of  find the product of matrices
find the product of matrices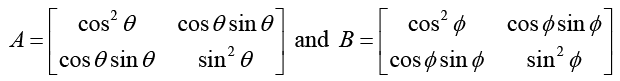
Ans.The product of A and B is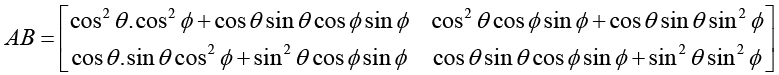
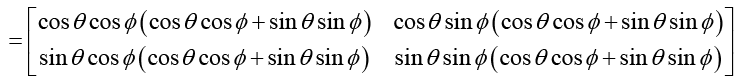
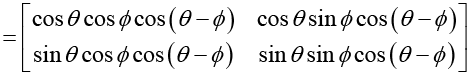
Since d and S differ by an odd multiple of 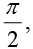 therefore θ - ∅ = an odd multiple of
therefore θ - ∅ = an odd multiple of 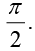
thus, cos (0-0) = 0. Hence, 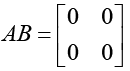
Q.2. Find the values of a, b, c, d, e, f where a, b, c and f are positive and d and e are negative such that the matrix 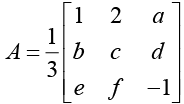 is orthogonal.
is orthogonal.
Ans. In an orthogonal matrix the sum of the squares of elements in any row or any columns is unity. Here, 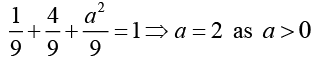
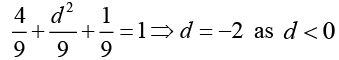

⇒ b2 + c2 = 5 and b+2c = 4
solving these two relation we obtain b = 2 and c = 1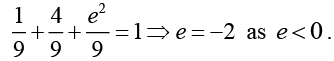
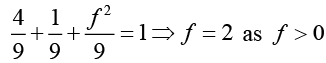
Q.3. If A is a matrix such that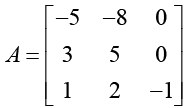
Find the matrix A20 + A15 + 2I, where I is 3 x 3 Identity matrix.
Ans. 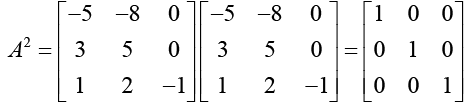
Thus, A2 = I, A3 = A, A4 = I, A5 = A and so on.
Thus we see that the odd power of A are equal to A and even powers of A are equal to I. Hence A20 + A15 + 21 = I + A + 2I = A + 3I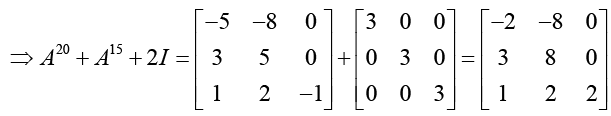
Q.4. The trace of a 3 x 3 matrix is 12 and the determinant of the matrix is 48 . The product of the smallest and the largest eigenvalues is 12. If all the eigenvalues of the matrix are different then
(a) Find the eigenvalues of the matrix.
(b) Write the chatacteristics equation.
Ans. λ1 + λ2 + λ3 = 12, λ1λ2λ3 = 48
Let A be the smallest eigenvalue and λ3 be the largest eigenvalue .
Then, λ1λ3 = 12 ⇒ λ2 = 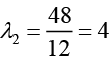
Hence, λ1 + λ3 = 8
(λ1 - λ3)2 = (λ1 + λ3)2 - 4λ1λ3 = 82 -4.12 =16 ⇒ λ1 - λ3 = + 4
λ1= 2 and λ3 = 6
(b) The characterstic equation is
(λ - 2)(λ - 4)(λ - 6) = 0 ⇒ λ3 -12λ2 + 44λ - 48 = 0
Q.5. Find the points where the curve represented by [ x y ] 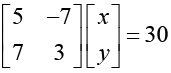 cuts the x and y axes.
cuts the x and y axes.
Ans. 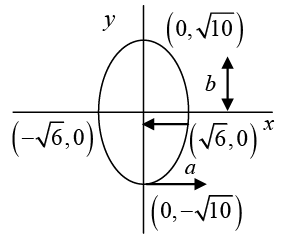
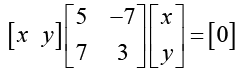

⇒ x (5x - 7 y) + y (7 x + 3 y ) = 30
5x2 + 3 y2 + ( 7 xy -7 xy) = 30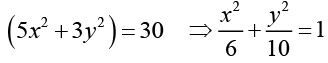
This is an equation of ellipse. Its graph is shown in the figure.
Q.6. Given the matrix B = 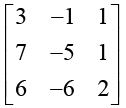
(a) Write the characteristic polynomial.
(b) If one of the eigenvalues of the matrix is twice repeated , find all the eigenvalues.
(c) Find the eigenvector associated with each eigenvalue.
Ans. (a) Tr (B) = 3 - 5 + 2 = 0, |B| = -16
Cofactors of diagonal elements are
B11 = -4, B22 = 0, B33 = -8
Therefore, P (A) = λ3 -12λ +16
(b) Since one of the eigenvalues of the matrix is twice repeated hence P (λ) and P'(λ) have the same roots.
P'(λ) = 3λ2 -12 ⇒ P'(λ) = 0 gives λ = ±2
Putting A = 2, makes P (λ) = 0 . Therefore λ = 2 is a twice repeated root.
From the property of roots we must have λ1λ2λ3 = -16 ⇒ 2 • 2 • λ = -16 ⇒ λ = -4. Thus λ = 2 is a twice repeated root and λ = -4 is another root.
(c) Subtracting λ = 2 down the main diagonal of B gives the matrix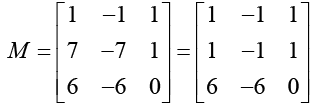
Here we have subtracted row 3 from row 2.
x1 - x2 + x3 = 0 and x3 = 0
This system has only one free variable hence 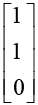 is an eigenvector.
is an eigenvector.
Q.7. For the matrix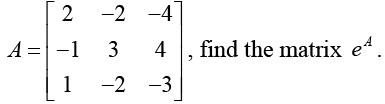
Ans. We see that A2 = A, i.e, A is an idempotent matrix. Therefore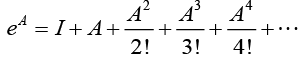
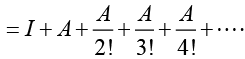
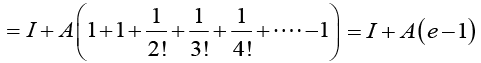
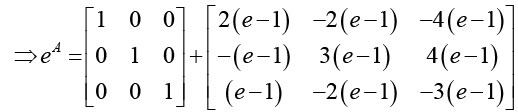
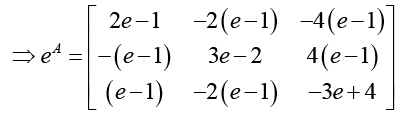
Q.8. Given the matrix
(a) Find the eigenvalue of matrix B .
(b) Find the eigenvectors of matrix B .
(c) Diagonalize matrix B .
(d) Find the matrix 
(e) Using Cayley-Hamilton’s theorem find the characteristic equation satisfied by matrix B .
(f) Are the eigenvectors of matrix B linearly independent? Are the eigenvectors orthogonal to each other?
Ans. (a) eigenvalves of B
⇒ (1 - λ)( 2 - λ)(3 - λ) = 0
⇒ λ = 1,λ = 2 and λ = 3
(b) Eigenvectors of B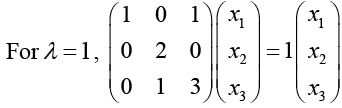
x1 + x3 = x1 ⇒ x3 = 0
2x2 = x2 ⇒ x2 = 0
x2 + 3x3 = x3
For λ = 2,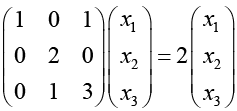
x1 + x3 = 2x1 ⇒ x3 = x1
2x2 = 2x2
x2 + 3x3 = 2x3 x2 = -x3
x1 + x3 = 3x1 ⇒ x3 = 2x1
2x2 = 3x2 ⇒ x2 = 0
x2 + 3x3 = 3x3
(c) We can take  as three eigenvectors corresponding to λ = 1,λ = 2 and λ = 3. The matrix P diagonalizing matrix B is
as three eigenvectors corresponding to λ = 1,λ = 2 and λ = 3. The matrix P diagonalizing matrix B is
Hence P-1AP = D, where D = 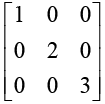
(d) we can write B = PDP-1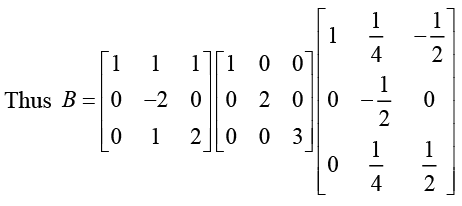
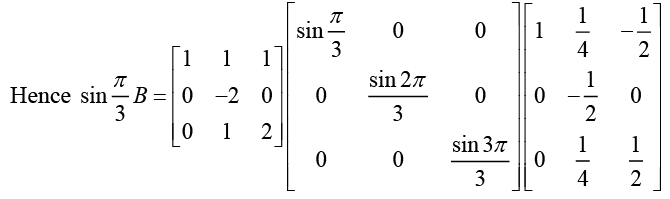
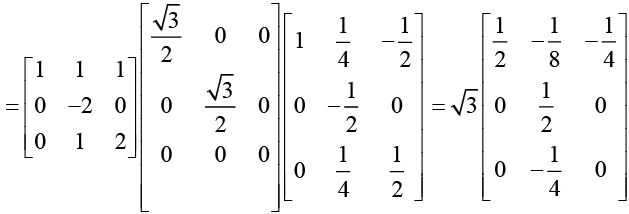
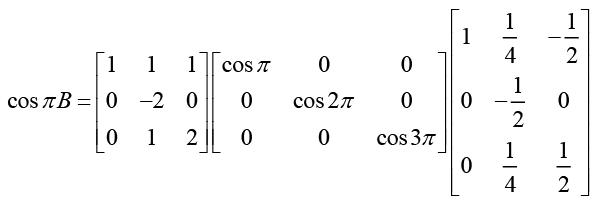
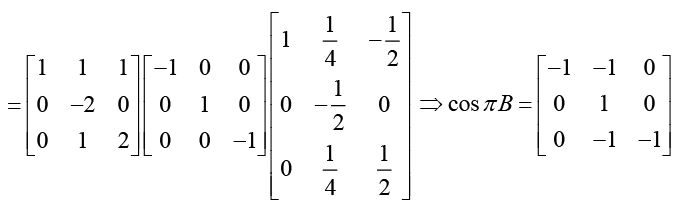
(e) The characteristic polynomial of the matrix is
P(λ) = (λ-1)(λ-2)(λ-3) = λ3 -6λ2 + 11λ - 6
Hence, according to Cayley-Hamiltoris theorem matrix equation satisfied by matrix B is B3 - 6B2 + 11B - 6I = 0
(f) We know that the eigenvectors belonging to distinct eigenvalves are linearly independent . Hence the eigenvalves of B corresponding to λ = 1,λ = 2 and λ = 3 are linearly independent. 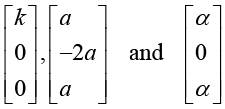 are the eigenvectors corresponding to λ = 1,λ = 2 and λ = 3 respectively.
are the eigenvectors corresponding to λ = 1,λ = 2 and λ = 3 respectively.
From orthogonality condition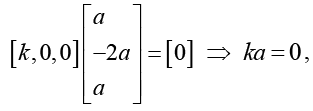
which is possible only when either k = 0 or a = 0. But k = 0 and a = 0 is not allowed. 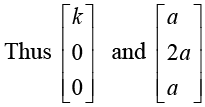 are not orthogonal. Similarly we see that no pair of eigenvectors are orthogonal.
are not orthogonal. Similarly we see that no pair of eigenvectors are orthogonal.
Q.9. If A and B are two matrices such that AB and A + B are both defined. What can be said about the relation between the order of the two matrices? Are A and B square?
Ans. Let A be an m x n matrix. Since A + B is defined, therefore B should also be an m x n . Further since AB in defined, hence m = n , hence A and B are square matrices of the same order.
Q.10. Let A, B, C and D be four non -zero matrices such that A = 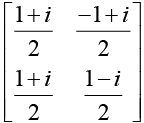
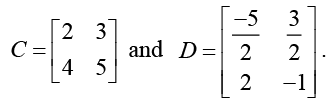 If AB = CD , find matrix B.
If AB = CD , find matrix B.
Ans. 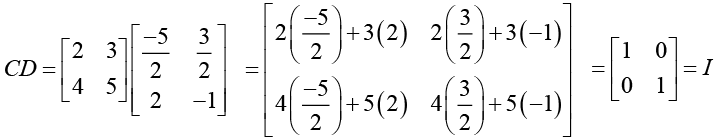
Since AB = CD ⇒ AB = I
Hence matrix B is the inverse of matrix A.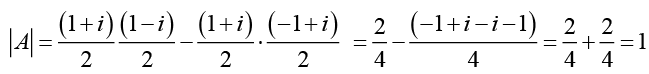
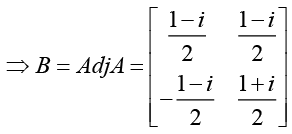
Q.11. If A is a matrix such that A = 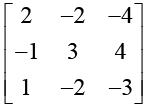 then
then
(a) Find matrix A100 + A99 + A98 + A97 + A2 + A .
(b) Find the Trace of matrix in part (a).
(c) Find the Determinant of matrix in part (a).
Ans. (a)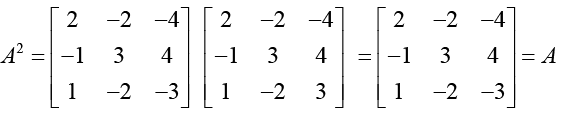
⇒ A3 = AA2 = A2 = A, A4 = A2 = AA5 = A2 = A....
Thus we have see that all powers of A are equation to A, hence we can write
A100 + A99 + A98 + A97 + ••• A2 + A
= A + A + A + ••• upto hundred times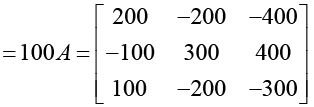
(b) The Trace of A100 + A99 + A98 + A97 + ••• A2 + A = 200+300 - 300 = 200
(c) The determinant of A100 + A99 + A98 + ••• A2 + A is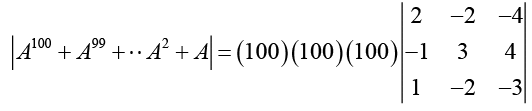
= 106 [2 (-9 [ 8) + 2 (3 - 4)-4 (2 - 3)] = 0
Q.12. If A and B are two matrices such that AB = A and BA = B . If A2 + B2 = 2α (A + B) then find the value of α .
Ans. We have AB = A
⇒ A (BA) = A[∴B = BA]
AB)A = A = A2 = A (i)
Again BA = B ⇒ BAB = B (Since A = AB)
(BA)B = B ⇒ B2 = B (ii)
Adding equations (i) and (ii)
A2 + B2 = A + B (iii)
From the question
A2 + B2 = 2α (A + B) (iv)
From (iii) and (iv) 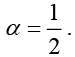
Q.13. If 
(a) Find Tr (A) + Tr (B ) + Tr (C ).
(b) Find Tr (AT ) Tr (BT ).Tr (CT ).
(c) Find Tr (A-1 ).Tr ( B-1) Tr (C-1).
(d) Find the product of determinant of three matrices.
Ans. |A| = (8 - 0)-2 (0 - 0) + 3 (0 - 0) = 8
|B| = 2 (12 - 0) = 24
|C| =10
Since the eigenvalues of a triangular or diagonal matrix are just the diagonal elements hence
(a) Tr ( A) + Tr (B) + Tr (C ) = 7 + 9 + 8 = 24
(b) Tr (AT) - Tr (BT)• Tr (CT ) = 7 • 9 • 8 = 504
(c) Tr (A-1)• Tr (B-1)• Tr (C-1) = 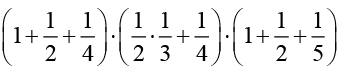
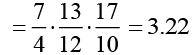
(d) det ( A)• det ( B )• det (C)
=8 x 24 x 10
= 1920
Q.14. Given the matrices A = 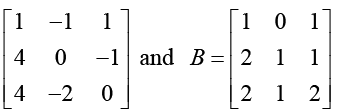
(a) Calculate B-1 AB and B-1A-1B.
(b) What is the relation between the two matrices of part (a)
Ans. 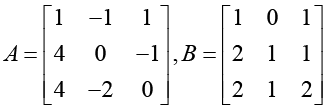
|A| = [0 - 2] +1[0 + 4] + [-8 - 0] = -6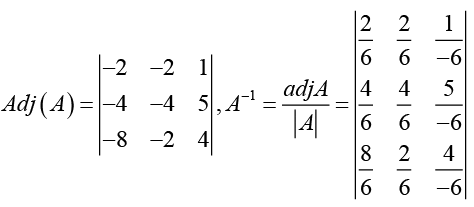
|B| = 1 + 0 + 1 x 0 = 1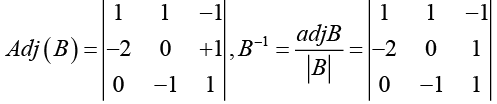
(a) 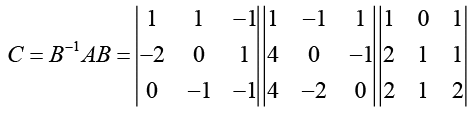
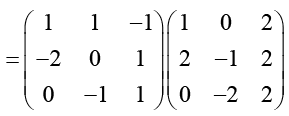
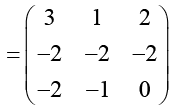
And, D = B-1 A-1B =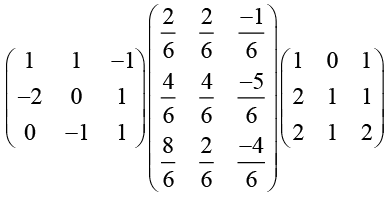
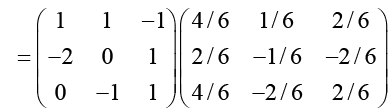
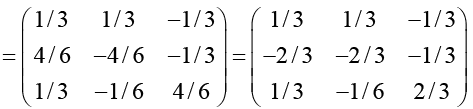
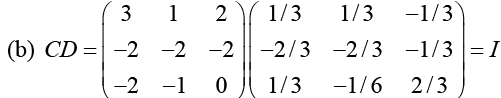
Q.15. Let  .If A = 3 is one of the eigenvalues of the matrix then
.If A = 3 is one of the eigenvalues of the matrix then
(a) Find other eigenvalues of the matrix.
(b) To each of the eigenvalues of the matrix find the associated eigenvectors.
Ans. (a) The characteristic polynomial of the given matrix is
P(λ) = λ3 -Tr(A)λ2 +(A11 + A22 + A33)λ - 
Where Tr (A) is the trace of matrix A. A11, A22 and A33 are cofactors of diagonal elements and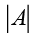 is the determinant of matrix A .
is the determinant of matrix A .
Here, Tr(A) = 4 + 5 + 2 = 11 and |A| = 4(l2)-1(6)-1(-3) = 45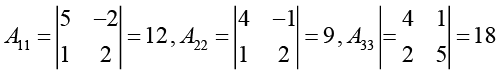
⇒ P (2) = λ3-11λ2 + 39λ-45
Since A = 3 is a root of this polynomial hence (A-3) is a factor of P(λ). Dividing P(λ) by A-3 we obtain
P(λ) = (λ-3)(λ2 -8λ +15) = (λ-3)(λ-3)(λ-5)
Thus, λ = 3 is a repeated eigenvalue. And λ = 3 is another eigenvalue.
(b) Subtracting λ = 3 down the diagonal of matrix A we obtain the matrix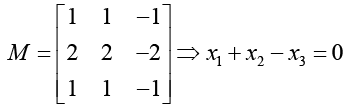
Hence we can take (1,-1,0) and (1,0,1) as two linearly independent eigenvalues. Subtracting λ = 5 down the matrix diagonal gives the matrix.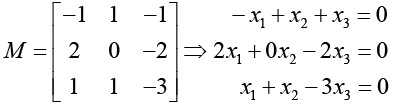
Thus, x1 - x3 = 0
X2 - 2 x3 = 0
Here we have only one free variable, hence (1,2,1) is an eigenvector corresponding to A = 5.
Q.16. For the matrix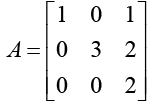
(a) Find the eigenvalues and eigenvectors .
(b) Find the matrix P which digonalizes matrix A .
(c) Write the diagonal form of A .
(d) Find the Trace and determinant of matrix e2A .
Ans. (a) Given 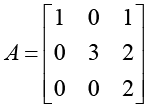
Solving above matrix for eigenvalues: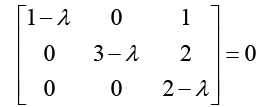
⇒ (2 - λ)(1 - λ)(3 - λ) = 0
λ = 1, λ2 = 3, λ3 = 2
Eigenvectors corresponding to respective eigenvalues, on solving we get as: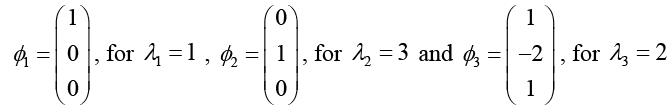
(b) Since we have three linearly independent eigenvectors, we can digonalise matrix A . Putting the eigenvectors of A as column vectors , we obtain
(c) Now, inverse of P is
Thus, Diagonalised matrix of given matrix A is
D = P-1AP
(d) The eigenvalues of matrix e2A are e2,e4, and e6.
Hence the trace of e2A is e2 (1 + e2 + e4)
The determinant of e2A is e2.e4.e6 = e12
Q.17. For the Pauli’s spin matrices
(a) Find the matrix 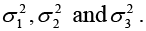
(b) Find the inverse of each of Pauli’s spin matrices.
(c) Find the eigenvalves of each Pauli’s spin matrix.
(d) Find the normalized Eigenvectors of each Pauli’s spin matrix.
(e) Diagonalize each of the Pauli’s matrices.
(f) Find the trace and determinant of matrix 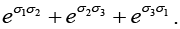
(g) Find the matrices 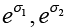 and
and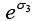
(h) Find the trace and determinant of matrix 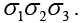
Ans. (a) 
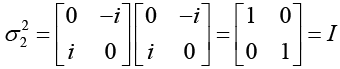
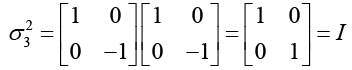
(b) From the above relation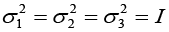 we see that each Pauli’s spin matrix its
we see that each Pauli’s spin matrix its
own inverse. A matrix which is its own inverse is called involutory. Thus each Pauli’s spin matrix is involutory.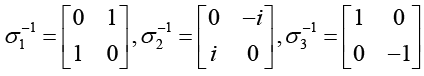
(c) Eigenvalues of 

Eigenvalues of 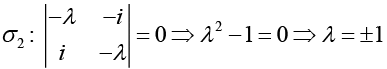
Eigenvalues of 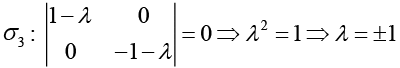
We see that the Eigenvalues of each Pauli’s spin matrices are ±1.
(d) Eigenvectors of σ1:
For λ = 1, we have , 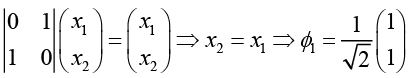
For λ = -1 ,we have, 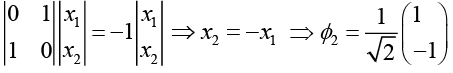
Eigen vectors of σ2
For λ = 1, we have , 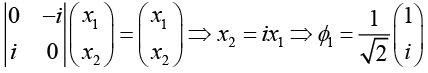
For λ = -1, we have , 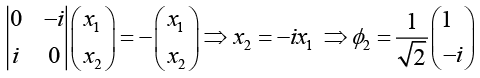
Eigen vectors of σ3 are, 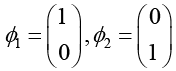
(e) Diagonalisation of σ1,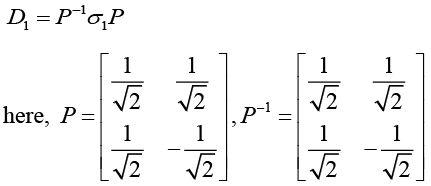
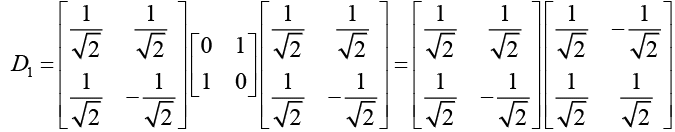
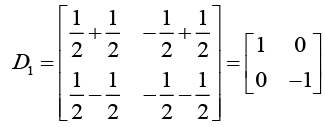
Diagonalisation of σ2,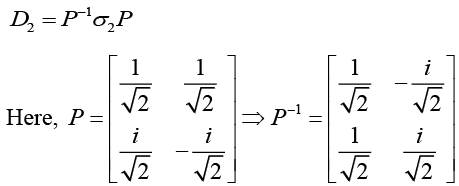
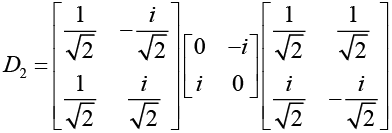
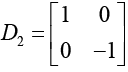
σ3 is already diagonalised.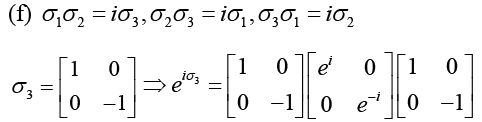
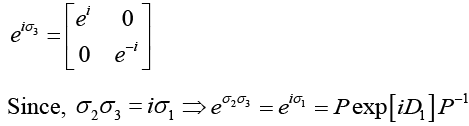
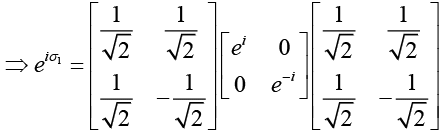
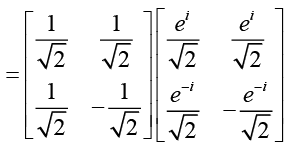
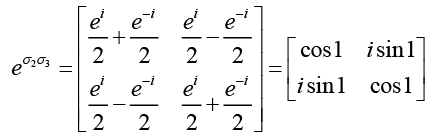
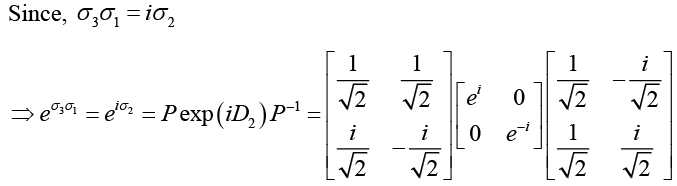
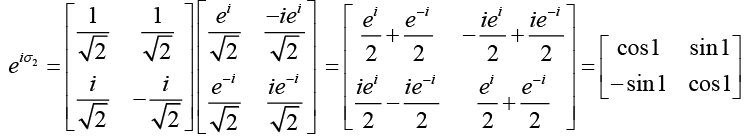
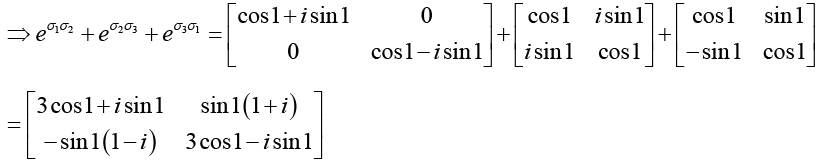
(g) 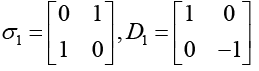
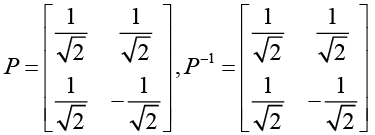
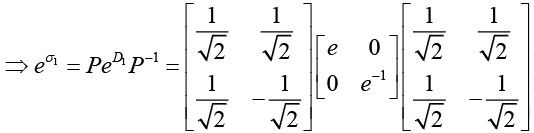
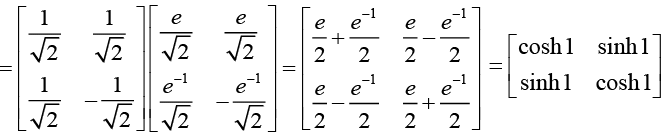
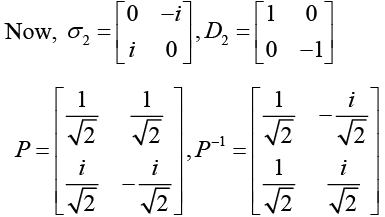
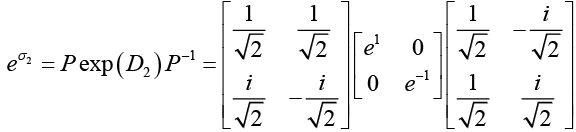
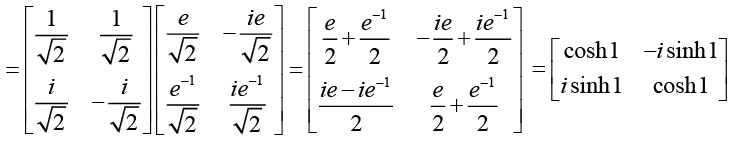
Now, 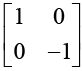 Since σ3 is diagonal we obtain
Since σ3 is diagonal we obtain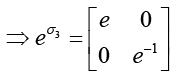
(h) σ1σ2σ3
As, σ1σ2 = iσ3 ⇒ σ1σ2σ3 = 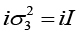
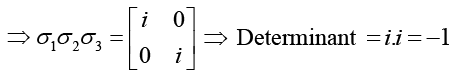
Trace λ1 + λ2 = i + i = 2i
|
78 videos|18 docs|24 tests
|
FAQs on Linear Algebra: Matrices - Assignment - Mathematical Methods - Physics
| 1. What is linear algebra and why is it important in mathematics? |  |
| 2. What is a matrix and how is it used in linear algebra? |  |
| 3. How do you multiply two matrices together? |  |
| 4. What is the determinant of a matrix and what does it signify? |  |
| 5. How can linear algebra be applied in real-world problems? |  |



















