Chapter Notes - Maths - Decimals
| Table of contents |

|
| Tenths |

|
| Hundredths |

|
| Thousandths |

|
| Expanded Form |

|
| Equivalent Decimals |

|
| Money and Decimals |

|
Decimals are a special way to write fractions as numbers. They use a dot called a decimal point to separate the whole number part from the fractional part.

In decimals, the numbers after the decimal point show the parts that are less than a whole number. Each digit in a decimal has a special role based on where it is located in relation to the decimal point.
Tenths
There are ten children attending Pooja’s birthday party. Her mother cuts the cake into 10 equal parts. Each part is one-tenth of the whole cake.
Look at the following figures
Each of the rectangles has been divided into ten equal parts. How many parts are shaded? The fraction is written below each figure. The denominator of these fractions is 10. These are special types of fractions called decimal fractions.
The denominator of these fractions is 10. These are special types of fractions called decimal fractions.
A fraction with denominator 10, 100, 1000, ... is called a decimal number or simply decimal.
- The fraction 1 / 10 (one-tenth) can be written as 0.1.
- Similarly, 4 / 10 is written as 0.4 and 9/10 is written as 0.9.
- The numerals 0.1, 0.4 and 0.9 are called decimal numerals or simply decimals. The dot in 0.1, 0.4 and 0.9 is called a decimal point. 0.1 can be read in two ways as under:
 This system of writing numbers with a decimal point is called the decimal system.
This system of writing numbers with a decimal point is called the decimal system.
Edurev Tips: The convention is to write a decimal numeral for a fraction like 5 / 10 as 0.5 and not .5. A zero is put before the point in 0.5. Thus, 1 / 10 is 0.1, 2 / 10 is 0.2, 3 / 10 is 0.3 and so on.
Decimals and Whole Numbers
Whole numbers can also be renamed using a decimal point.
For example: 1 = 1.0; 3 = 3.0; 5 = 5.0; 7 = 7.0; 9 = 9.0
The zero after the decimal point means there are 0 tenths.
More than One (Mixed Numbers and Mixed Decimals)
 You can use a mixed decimal to name a mixed number.
You can use a mixed decimal to name a mixed number.  and 3.6 are both read as “three and six-tenths.”
and 3.6 are both read as “three and six-tenths.”
The table below illustrates different ways of reading and writing tenths. The zero after the decimal point means there are 0 tenths.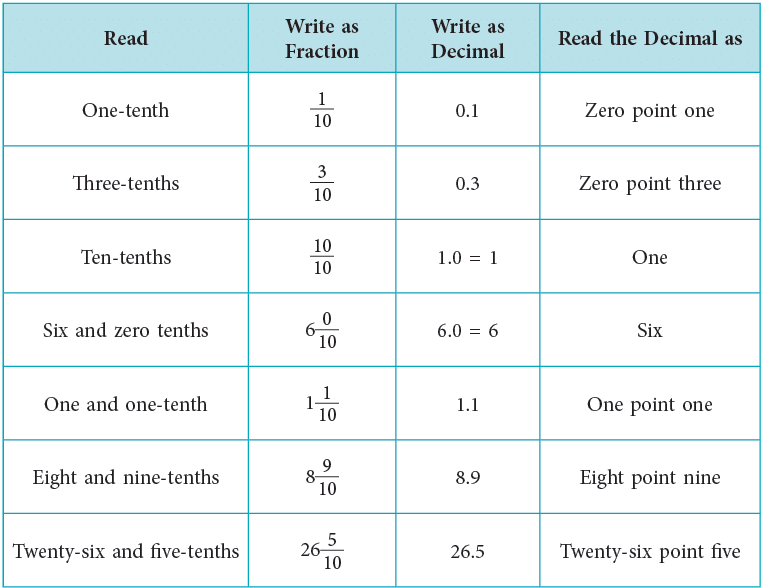
The decimal numbers can also be shown on a number line. The following picture shows a number line which has been divided into tenths.
Hundredths
There are 100 small squares in the large square. 1 small square is one -hundredth or 1 / 100 of the large square. The shaded part consists of 9 small squares. 9 small squares make “nine-hundredths” of the large square. We say that the shaded part is 9 / 100 or 0.09. Since there are two zeros in the denominator of 9 / 100, therefore, there are two digits to the right of the decimal point in 0.09.
Since there are two zeros in the denominator of 9 / 100, therefore, there are two digits to the right of the decimal point in 0.09.
Now, look at the adjacent figure: The shaded part is “thirty-three” hundredths of the large square.
The shaded part is “thirty-three” hundredths of the large square.
Notice that there are two digits after the decimal point when writing a decimal to show hundredths.
Reading a Decimal Number

The following diagrams are drawn to help you gain complete understanding:
0.04 = 0 tenth and 4 hundreds
0.10 = 1 tenth and 0 hundredths
0.45 = 4 tenths and 5 hundredths
0.83 = 8 tenths and 3 hundredths
Writing Mixed Decimals for a Mixed Number
A mixed decimal can be written for a mixed number as under:
From the above examples, we can see that:
A decimal number is made up of two parts: a whole number part and a decimal part separated by a decimal point. The number of digits after the decimal point is known as the number of decimal places.
For example: 31.9 has one decimal place.
583.28 has two decimal places.
Thousandths
One-thousandth means 1 / 1000. If you divide a square into 1000 small squares, then one small square denotes one-thousandth part or 1 / 1000, which is written in decimal form as 0.001.
1 / 10 = 0.1 meaning one-tenth
1 / 100 = 0.01 meaning one-hundredth
1 / 1000 = 0.001 meaning one-thousandth
The decimal number 0.001 is read as zero point zero zero one. Similarly, we have,
Edurev Tips: Since there are three zeros in the denominator, therefore, there are three digits to the right of the decimal point.
You can read and write thousandths in different ways as given below in the table.
Thus, the number of digits after the decimal point is the same as the number of zeros in the denominator of the fraction.
Edurev Tips: The digits after the decimal point are read one by one. For example, 17.035 is read as seventeen point zero three five and not as sevaenteen point thirty-five.
Decimal Fractions in the Place Value Chart
The place value chart that you have studied till now can be shown as follows:
Starting from the left and moving towards the right,
As we move towards the right, each place value becomes one-tenth of the previous one.
Observing the above pattern, you can now guess that to show one-tenth, one-hundredth and one-thousandth on the place value chart, we have to extend it to the right of ones.
Thus, the place value chart extended beyond ones to the right is as given below.
For example, the decimal number 683.459 can be shown in the place value chart as:
Example 1: Find the place value of each digit in 625.378.
Expanded Form
Let us write the expanded form for the number 634.957.
634.957 = 6 hundreds + 3 tens + 4 ones + 9 tenths + 5 hundredths + 7 thousandths
This is the expanded form of the number 634.957.
We give some more examples to help you get better understanding.
Example: Write each decimal numeral in expanded form.
(a) 5.86
(b) 0 .476
(c) 6 5.26
(d) 3 92.067
Sol: (a) 5.86 = 5 ones + 8 tenths + 6 hundredths
(b) 0.476 = 4 tenths + 7 hundredths + 6 thousandths
(c) 65.26 = 6 tens + 5 ones + 2 tenths + 6 hundredths
(d) 392.067 = 3 hundreds + 9 tens + 2 ones + 0 tenths + 6 hundredths + 7 thousandths
Equivalent Decimals
The shaded square on the right shows that:
0.2 = 0.20 Thus, we can rename a decimal by writing as many zeros as we like after the last digit in a decimal number.
Thus, we can rename a decimal by writing as many zeros as we like after the last digit in a decimal number.
We have, 0.5 = 0.50 = 0.500 = 0.5000 etc.
Tenths can be renamed as hundredths as well as thousandths: 0.1 = 0.10 = 0.100.
Hundredths can be renamed as thousandths: 0.08 = 0.080; 0.37 = 0.370.
Money and Decimals
You know that 100 paise makes 1 rupee, i.e., 100 p = 1 rupee or ₹ 1.
Therefore,
Hence, 3 rupees 50 paise is written as ₹ 3.50 and read as rupees three and fifty paise. In the same way, rupees six and forty paise is written as ₹ 6.40.
Also, one hundred eighty-four rupees and seventy-five paise in figures is written as ₹ 184.75. This shows that we use a decimal point to separate rupees from paise.
Conversions of Rupees to Paise
To convert rupees into paise, we multiply the amount in rupees by 100.
Examples: Convert the following into paise
(i) ₹ 7
Sol: ₹ 7 = 7 × 100 p = 700 p
(ii) ₹ 69
Sol: ₹ 69 = 69 × 100 p = 6900 p
(iii) ₹ 225
Sol: ₹ 225 = 225 × 100 p = 22500 p
To convert rupees and paise into paise, multiply the amount in rupees by 100 and add it to the number of paise.
Example: Convert ₹ 25.30 into paise.
Sol: ₹ 25.30 = 25 rupees 30 paise
= 25 × 100 p + 30 p
= 2500 p + 30 p = 2530 p;
₹ 20.55 = 2055 p; ₹ 89.60 = 8960 p;
₹ 128.25 = 12825 p
Edurev Tips: In fact, you can just remove the decimal point to get the number of paise.
Conversion of Paise to Rupees
To convert paise into rupees or rupees and paise, we divide the amount by 100.
To convert paise into rupees and paise, we put a dot (.) after 2 digits from the right of the given number showing paise. The numeral on the left of the dot indicates the number of rupees and that on the right of the dot indicates the number of paise.
Example: Convert the following into rupees

(i) 4806 paise
Sol: 4806 paise = ₹ 48.06 = 48 rupees 6 paise
(ii) 89 paise
Sol: 89 paise = ₹ 0.89
(iii) 210 paise
Sol: 210 paise = ₹ 2.10 = 2 rupees 10 paise
[Intext Question]
Addition and Subtraction of Money
While adding and subtracting money, take care to place the decimal (point) exactly one below the other and then add or subtract like you add or subtract any other numbers.
Remember to put the decimal in the same place (two digits from the right) in the answer.
Example: Shyam purchased a pencil worth ₹ 3.40 and an eraser worth ₹ 2.10. How much did he spend in all?
Sol: Cost of pencil = ₹ 3.40
Cost of eraser = ₹ 2.10
Step 1: Arrange the amount in proper columns.
Step 2: Add as ordinary numbers.
Step 3: Place the decimal point to separate rupees from paise.
Hence, Shyam spent ₹ 5.50 in all.
Example: Amit carried ₹ 5.40 to a shop. He bought a candy worth ₹ 1.20. How much money did he take back home?
Sol:
Total money Amit had = ₹ 5.40Cost of candy = ₹ 1.20
Therefore, the money left with Amit,
Hence, the amount that Amit took back home = ₹ 4.20.
Example: Find the total money due in the bill given alongside. If a 100-rupee note and a 50-rupee note were paid to the shopkeeper, then what was the amount received as change?
Sol: Total amount of money = ₹ 100 + ₹ 50 = ₹ 150
Amount paid to the shopkeeper = ₹( 10.50 + 42.25 + 42.25 + 15.75) = ₹110.75
Amount received as a change = ₹ 150 – ₹ 110.75 = ₹ 39.25
Hence, the amount received as change = ₹ 39.25.
Multiplication of Money
Multiplication of money is done in the same way as you would multiply whole numbers. However, we must not forget to put the decimal point after two digits from the right in the product.
Example: How much will 3 ice creams cost if each costs ₹ 16.50?
Sol: Cost of each ice cream = ₹ 16.50
Total number of ice creams = 3
Step 1: Arrange the numbers properly and multiply as ordinary numbers.
Step 2: Put a decimal point two places from the right in the answer.
Thus, 3 ice creams will cost ₹ 49.50.
Example: Heena bought 15 pairs of earrings, each pair costing ₹ 8.50. How much change did she get back from ₹ 150?
Sol: Cost of 1 pair of earrings = ₹ 8.50
Cost of 15 pairs of earrings = ₹ 8.50 × 15 = ₹ 127.50
Amount she got back = ₹ 150.00 – ₹ 127.50
= ₹ 22.50
Hence, Heena got ₹ 22.50 back as change.
Division of Money by a Whole Number
- Divide as ordinary numbers.
- Place the decimal point in the quotient above the point in the dividend.
Example: Aisha paid ₹ 513.18 for 9 books. How much did she pay for each book?
Sol: Total amount paid by Aisha = ₹ 513.18
Total number of books = 9
Hence, Aisha paid ₹ 57.02 for each book.
Estimating Total Cost
Rule: For a quick mental estimate, round off each addend to its greatest place value and then add the rounded numbers.
Example: Harish and Ritesh went to a CD store to buy the following DVDs.

Estimate the total amount needed to purchase the above DVDs.
Sol:
Thus, the estimated total cost for the DVD’s is ₹ 1700.
|
30 videos|110 docs|30 tests
|
FAQs on Chapter Notes - Maths - Decimals
| 1. What are some examples of decimal place values? |  |
| 2. How can decimals be written in expanded form? |  |
| 3. What are equivalent decimals and how are they determined? |  |
| 4. How do decimals relate to money and currency? |  |
| 5. Can you explain the concept of hundredths and how they are used in decimals? |  |

|
Explore Courses for Class 4 exam
|

|
 This system of writing numbers with a decimal point is called the decimal system.
This system of writing numbers with a decimal point is called the decimal system.














 Hence, Aisha paid ₹ 57.02 for each book.
Hence, Aisha paid ₹ 57.02 for each book.


















