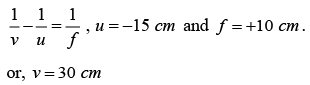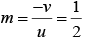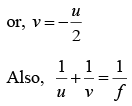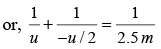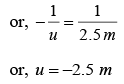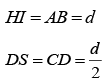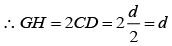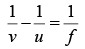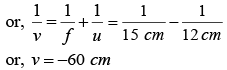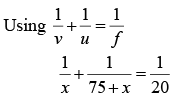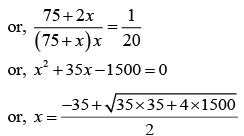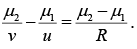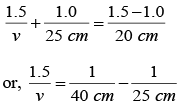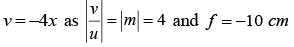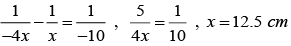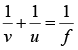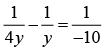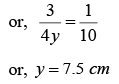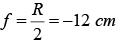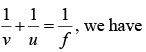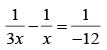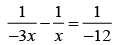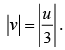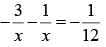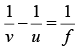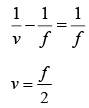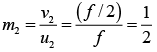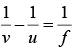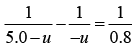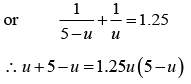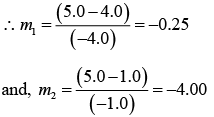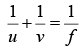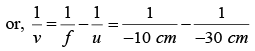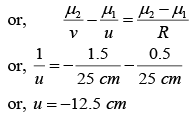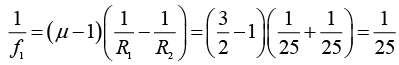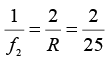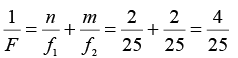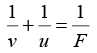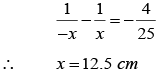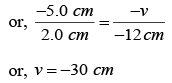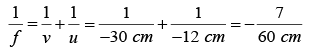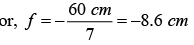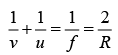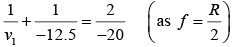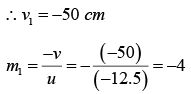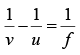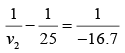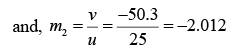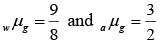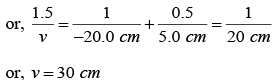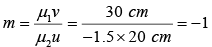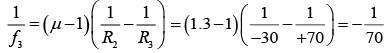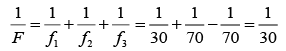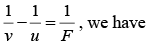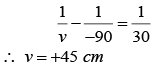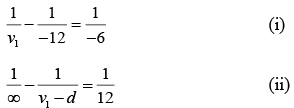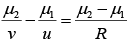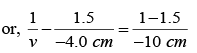Geometric Optics: Assignment | Oscillations, Waves & Optics - Physics PDF Download
Q.1. A point source S is placed at a distance of 15 cm from a converging lens of focal length 10 cm on its principal axis. Where should a diverging mirror of focal length 12 cm be placed so that a real image is formed on the source itself.
.
The equation for the lens is
The positive sign of v show that the image I1 is formed to the right of the lens in the figure. The diverging mirror is to be placed to the right in such a way that the light rays fall on the mirror perpendicularly. Then only the rays will retrace their path and form the final image on the object. Thus, the image I1 formed by the lens should be at the centre of curvature of the mirror.
Now, LI1 = 30cm , MI1 = R = 2f = 24 cm
Hence, LM = LI - MI1 = 6 cm
Thus, the mirror should be placed 6 cm to the right of lens.
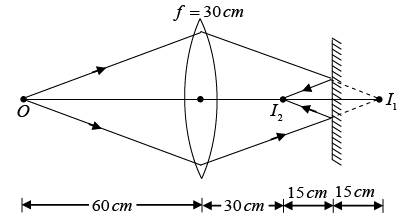
Q.2. A source of light is located at double focal length from a convergent lens. The focal length of the lens is f = 30 cm. At what distance from the lens should a flat mirror be placed, so that the rays reflected from the mirror are parallel after passing through the lens for the second time?
Object is at a distance of 2f = 60 cm from the lens. Image formed by lens I1, should be at a distance 60 cm from the lens. Now I2, the image formed by plane mirror should lie at focus or at a distance of 30 cm from the lens. Hence, the mirror should be placed at distance 45 cm from the lens as shown in figure.
Q.3. At what distance from a convex mirror of focal length 2.5 m should a boy stand so that his image has a height equal to half the original height? The principal axis is perpendicular to the height.
we have,
Thus, he should stand at a distance of 2.5 m from the mirror
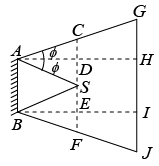
Q.4. A point source of light S placed at a distance L in front of the centre of a mirror of width d, hangs vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown. Calculate the greatest distance over which he can see the image of the light source in the mirror.
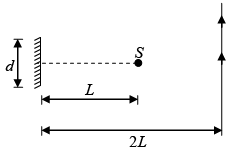
The ray diagram will be as shown in figure below.
Since, AH = 2 AD
Similarly, IJ = d
∴ GJ = GH + HI + IJ
= d +d +d =3d
Q.5. A converging lens of focal length 15 cm and a converging mirror of focal length 20 cm are placed with their principal axes coinciding. A point source S is placed on the principal axis at a distance of 12 cm from the lens as shown in figure below. It is found that the final beam comes out parallel to the principal axis. Find the separation between the mirror and the lens.

Let us first, locate the image of S formed by the lens. Here u =-12 cm and f = 15 cm . We have
The negative sign shows that the image is formed to the left of the lens as suggested in the figure. The image I1 , acts as the source for the mirror. The mirror forms an image I2 of the source I1. this image I2 then acts as the source for the lens and the final beam comes out parallel to the principal axis. Clearly I2 must be at the focus of the lens. We
have,
I1= I1P + PI2 = 60 cm + 15 cm = 75 cm
Suppose the distance of the mirror from I 2 is x cm . For the reflection from the mirror, u = MI1 = - (75 + x) cm, v = - x cm and f =-20 cm
this gives = x- 25 or -60 .
As the negative sign has no physical meaning, only positive sign should be taken. Taking x = 25 , the separation between the lens and the mirror is (15 + 25) cm= 40 cm.
Q.6. Locate the image formed by refraction in the situation shown in figure below. The point C is centre of curvature.
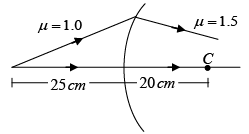
we have,
Here u = -25 cm, R = 20 cm, μ1 = 1.0 and μ2 = 1.5,
Putting the values in (i)
or, v =-100 cm
As v is negative, the image is formed to the left of the separating surface at a distance of 100 cm from it.
Q.7. Find the distance of object from a concave mirror of focal length 10 cm so that image size is four times the size of the object.
Concave mirror can form real as well as virtual image. Here nature of image is not given in the question. So we will consider two possible cases.
Case 1: (when image is real): Real image is formed on the same side of the object, i.e., u,v and f all are negative. So let,
u =-x
then,
Substituting in,
We have,Note: |x| >f and we know that in case of a concave mirror, image is real when object lies beyond F.
Case 2: (when image is virtual): In case of a mirror image is virtual, when it is formed behind the mirror, i.e., u and f are negative, while v is positive. So let u =-y
then v =+4y and f =-10 cm
Substituting in,
we have,
Note: |y| <|f| and we know that in case of a concave mirror, image is virtual when the object lies between F and P.
Q.8. A concave mirror has a radius of curvature of 24 cm . How far is an object from the mirror if an image is formed that is:
(a) virtual and 3.0 times the size of the object
(b) real and 3.0 times the size of the object and
(c) real and 1/ 3 the size of the object?
Given R =-24 cm
Hence,
(a) Image is virtual and 3 times large. Hence, u is negative and v is positive. Simultaneously |v| = 3|u|. So let,
u =-x
then, v =+3x
Substituting in the mirror formula
∴ x= 8 cm
therefore, object distance is x = 8 cm
(b) Image is real and 3 times large. Hence, u and v both are negative and |v| = 3|u|. So let,
u =-x
then v =-3x
Substituting in the mirror formula, we have
or, x = 16 cm
∴ Object distance should be 16 cm(c) Image is real and 1/3rd the size of object. Hence, both u and v are negative and
So let,
u =-x
then, v=-x/3
Substituting in the mirror formula, we have
or, x = 48 cm
∴ Object distance should be 48 cm
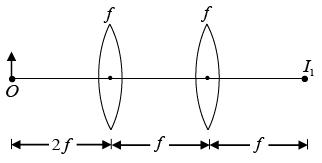
Q.9. Two thin converging lenses are placed on a common axis, so that the centre of one of the coincides with the focus of the other. An object is placed at a distance twice the focal length from the left-hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
The image formed by first lens will be at a distance 2f with lateral magnification
m1 =-1. From second lens this image will behave as a virtual object. Using the lens formula,
we have,
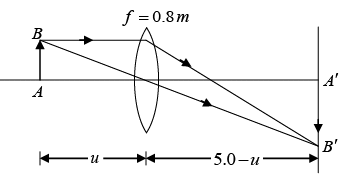
Q.10. An object is 5.0 m to the left of a flat screen. A converging lens for which the focal length is f = 0.8m is placed between object and screen.
(a) Show that two lens positions exist that form images on the screen and determine how far these positions are from the object?
(b) How do the two images differ from each other?
(a) Using the lens formula,
we have,
or , 1.25u2 - 6.25u + 5 = 0
or u = 4m and 1m
Both the values are real, which means there exist two positions of lens that form image of object on the screen.
(b) m = v/u
Hence, both the image is real and inverted, the first has magnification -0.25 and thesecond -4.00
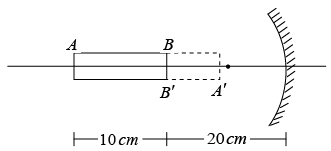
Q.11. A rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that the end closer to the pole is 20 cm away from it. Find the length of the image.
The situation is shown in figure. The radius of curvature of the mirror is r = 2 f= 20 cm. Thus, the nearer end B of the rod AB is at the centre of the curvature and hence, its image will be formed at B itself. We shall now locate the image of A.
Here u =-30 cm and f =-10 cm . We have
or, v =-15 cmThus, the image of A is formed at 15 cm from the pole. The length of the image is, therefore 5.0 cm.
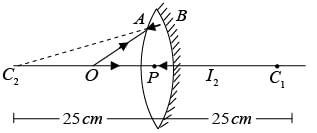
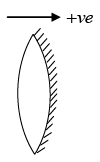
Q.12. A biconvex thin lens is prepared from glass (m = 1.5) , the two bounding surfaces having equal radii of 25 cm each. One of the surfaces is silvered from outside to make it reflecting. Where should an object be placed before this lens so that the image is formed on the object itself?
Refer to figure.
The object is placed at O.A ray starting from O gets refracted into the glass at the first surface and hits the silvered surface along AB. To get the image at the object, the rays should retrace their path after reflection from the silvered surface. Thus, AB should appear to come from the centre the first surface. Thus due to the refraction at the first surface, a virtual image of O is formed at C2. For this case,
v = -25 cm, R = +25 cm, μ1 = 1, μ2 = 1.5
we have,
Thus, the object should be placed at distance of 12.5 cm from the lens.
Q.13. A biconvex thin lens is prepared from glass of refractive index 3 / 2 . The two bounding surfaces have equal radii of 25 cm each. One of the surfaces is silvered from outside to make it reflecting. Where should an object be placed before this lens so that the image coincides with the object.
Refer extra points.
Here, R1 = +25 cm, R2 = -25 cm, μ1 = 1 and μ2= 3/2
Image coincides with object, hence, u = v = - x (say)
Focal length of lens
Focal length of concave mirror
Total Focal length of combination of lens and mirror
Lens formula,
Hence, the object should be placed at a distance 12.5 cm in front of the silvered lens.
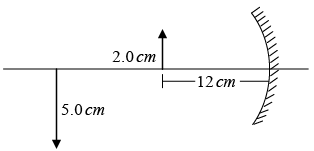
Q.14. A 2.0 cm high object is placed on the principal axis of a concave mirror at a distance of 12 cm from the pole. If the image is inverted, real and 5.0 cm high, find the location of the image and the focal length of the mirror.
The magnification is
m = -v/uThe image is formed at 30 cm from the pole on the side of the object, we have
the focal length of the mirror is 8.6 cm
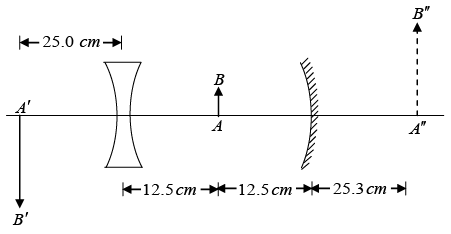
Q.15. The object is midway between the lens and the mirror. The mirror’s radius of curvature is 20.0 cm and the lens has focal length of -16.7 cm . Considering only the ray that leaves the object and travels first towards the mirror, locate the final image formed by this system. Is this image real or virtual? Is it upright or inverted? What is the overall magnification?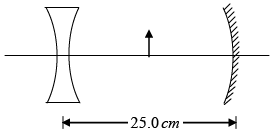
Image formed by mirror: Using mirror formula
we have,i.e., image formed by the mirror is at distance of 50 cm from the mirror to the left of it. It is inverted and four times larger.
Image formed by lens: Image formed by mirror acts as an object for lens. It is at a distance of 25.0 cm to the left of lens using the lens formula,
we have,
∴ v = -50.3 cm
overall magnification is m = m1 x m2 = 8.048
Thus, the final image is at a distance 25.3 cm to the right of the mirror, virtual, upright enlarged and 8.048 times. Positions of the two images are shown in figure.
Q.16. Refractive index of glass with respect to water is (9/8). Refractive index of glass with respect to air is (3/2). Find the refractive index of water with respect to air.
Given,
Q.17. One end of a horizontal cylindrical glass rod (μ = 1.5) of radius 5.0 cm is rounded in the shape of a hemisphere. An object 0.5 mm high is placed perpendicular to the axis of the rod at a distance of 20.0 cm from the rounded edge. Locate the image of the object and find its height.
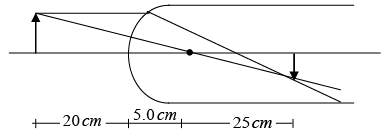
Taking the origin at the vertex, u =-20.0 cm
we have,
The image is formed inside the rod at a distance of 30 cm from the vertex
The magnification is
Thus, the image will be of same height ( 0.5 mm ) as the object but it will be inverted.
Q18. Two equi-convex lenses of focal lengths 30 cm and 70 cm , made of material of refractive index = 1.5 , are held in contact coaxially by a rubber band round their edges. A liquid of refractive index 1.3 is introduced in the space between the lenses filling it completely. Find the position of the image of a luminous point object placed on the axis of the combination lens at a distance of 90 cm from it.
|R1| = |R2| = f1 = 30 cm
Similarly, |R3| = |R4| = f2 = 70 cmThe focal length of the liquid lens (in air)
Further, equivalent focal length of the combination,
using the lens formulaThus, image will be formed at distance of 45 cm from the combination.
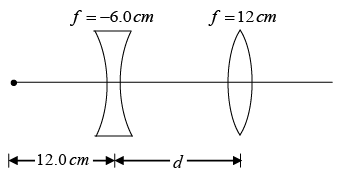
Q.19. An object is placed 12 cm to the left of a diverging lens of focal length -6.0 cm. A converging lens with a focal length of 12.0 cm is placed at a distance d to the right of the diverging lens. Find the distance d that corresponds to a final image at infinity.
Applying lens formula
twice we have,
Solving equations (i) and (ii), we have
v1 =-4 cm and, d = 8 cm
Q.20. There is a small air bubble inside a glass sphere (m = 1.5) of radius 10 cm . The bubble is 4.0 cm below the surface and is viewed normally from the outside (figure below). Find the apparent depth of the bubble.
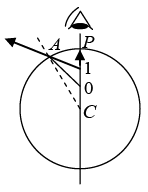
The observer sees the image formed due to refraction at the spherical surface when the light from the bubble goes from the glass to the air.
Here u = -4.0 cm, R = -10 cm, μ1 = 1.5 and μ2 = 1
We have,
or, v = -3.0 cm.Thus, the bubble will appear 3.0 cm below the surface.
|
54 videos|22 docs|14 tests
|
FAQs on Geometric Optics: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is geometric optics? |  |
| 2. What is the significance of geometric optics in IIT JAM exam? |  |
| 3. How can I prepare for the geometric optics section in the IIT JAM exam? |  |
| 4. Can you provide some examples of questions related to geometric optics in the IIT JAM exam? |  |
| 5. Are there any specific formulas or equations that I should remember for the geometric optics section in the IIT JAM exam? |  |