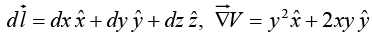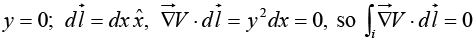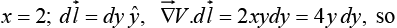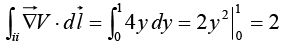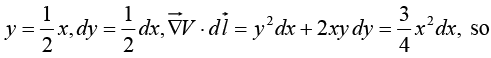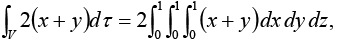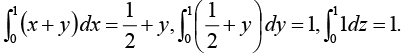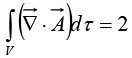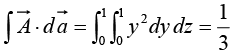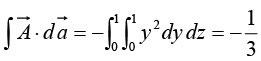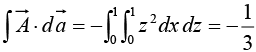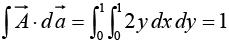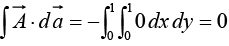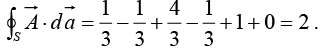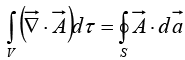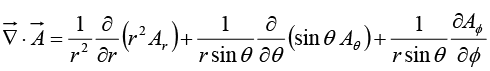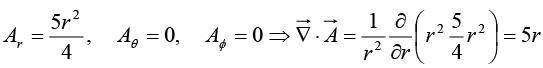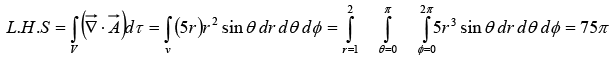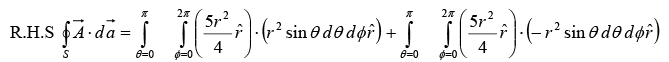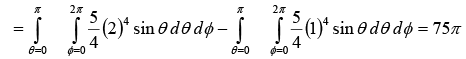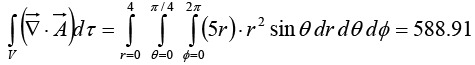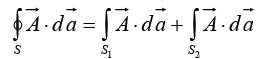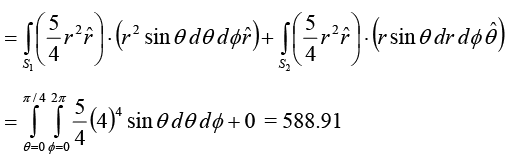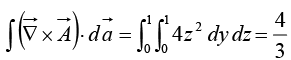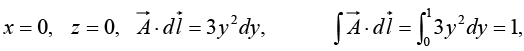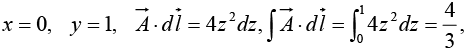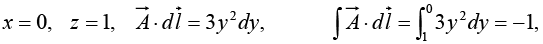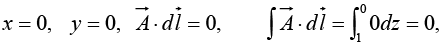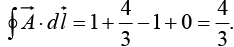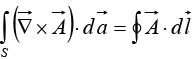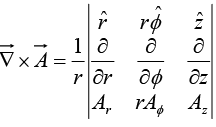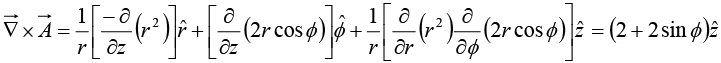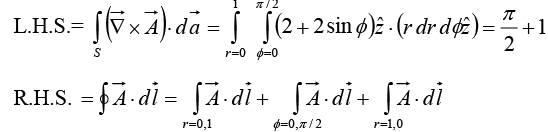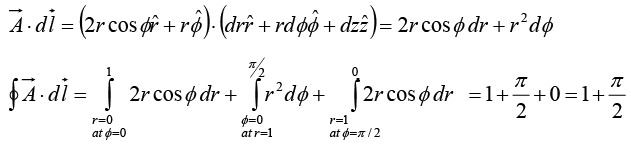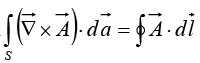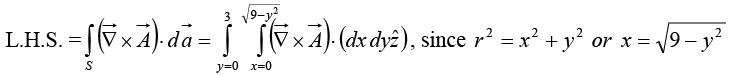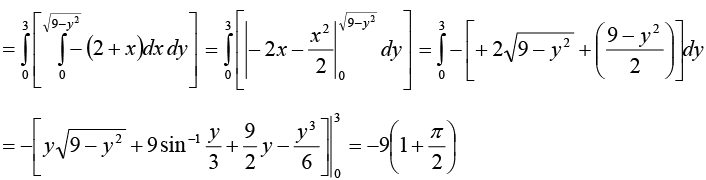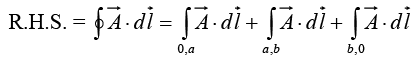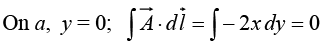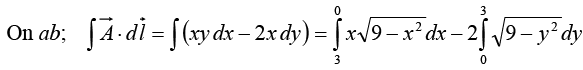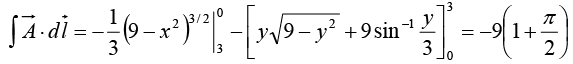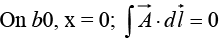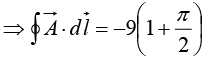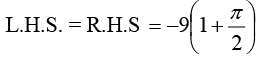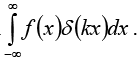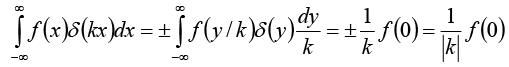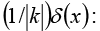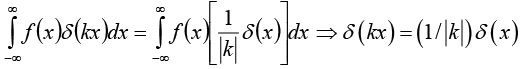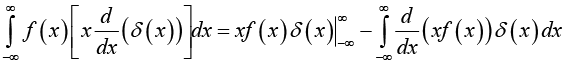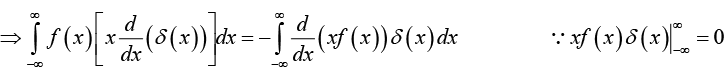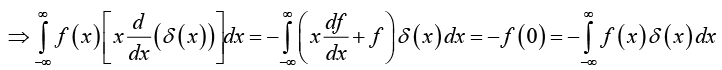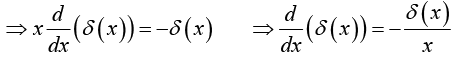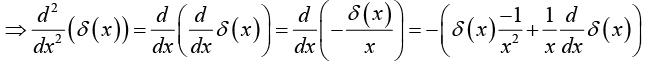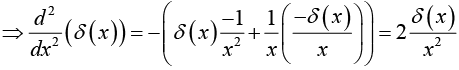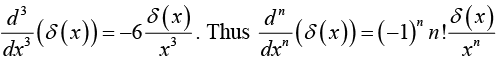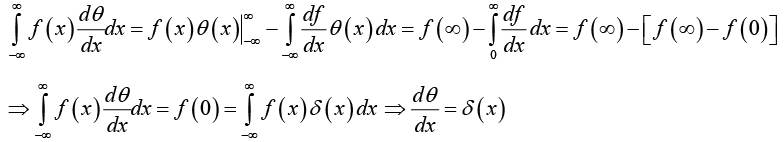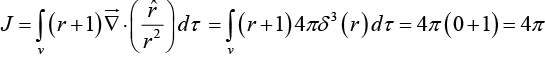Fundamental Theorems & Dirac Delta Function | Mathematical Methods - Physics PDF Download
The Fundamental Theorem of Calculus
Suppose f (x) is a function of one variable. The fundamental theorem of calculus states: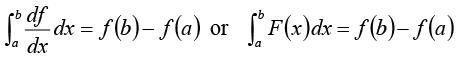
where df /dx = F(x).
Geometrical Interpretation
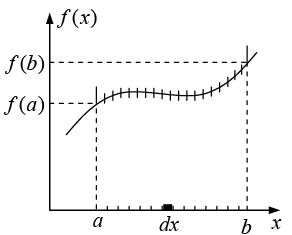
According to equation df = (df /dx) dx is the infinitesimal change in f when one goes from (x) to (x + dx). The fundamental theorem says that if you chop the interval from a to b into many tiny pieces, dx, and add up the increments df from each little piece, the result is equal to the total change in f is f (b) – f (a). In other words, there are two ways to determine the total change in the function: either subtract the values at the ends or go step-by-step, adding up all the tiny increments as you go. You’ll get the same answer either way.
The Fundamental Theorem for Gradients
Suppose we have a scalar function of three variables V(x, y, z). Starting at point a, we moves a small distance 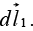 Then
Then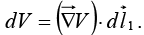
Now we move a little further, by an additional small displacement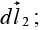 the incremental change in V will be
the incremental change in V will be 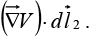 In this manner, proceeding by infinitesimal steps, we make the journey to point b. At each step we compute the gradient of V (at that point) and dot it into the displacement
In this manner, proceeding by infinitesimal steps, we make the journey to point b. At each step we compute the gradient of V (at that point) and dot it into the displacement 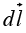 …this gives us the change in V. Evidently the total change in V in going from a to b along the path selected is
…this gives us the change in V. Evidently the total change in V in going from a to b along the path selected is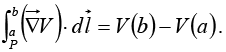
This is called the fundamental theorem for gradients; like the “ordinary” fundamental theorem, it says that the integral (here a line integral) of a derivative (here the gradient) is given by the value of the function at the boundaries (a and b).
Geometrical Interpretation
Suppose you wanted to determine the height of the Eiffel Tower. You could climb the stairs, using a ruler to measure the rise at each step, and adding them all up or you could place altimeters at the top and the bottom, and subtract the two readings; you should get the same answer either way (that's the fundamental theorem).
Corollary 1: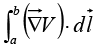 is independent of path taken from a to b.
is independent of path taken from a to b.
Corollary 2: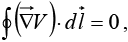 since the beginning and end points are identical, and hence
since the beginning and end points are identical, and hence
V(b) – V(a) = 0.
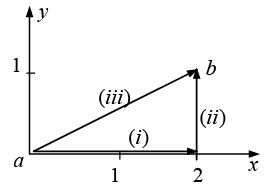
Example 22: Let V = xy2, and take point a to be the origin (0, 0, 0) and b the point (2, 1, 0). Check the fundamental theorem for gradients.
Although the integral is independent of path, we must pick a specific path in order to evaluate it. Let's go out along the x axis (step i) and then up (step ii). As always,
(i)
(ii)
Evidently the total line integral is 2. This consistent with the fundamental theorem: T(b) – T(a) =2 – 0 = 2.
Calculate the same integral along path (iii) (the straight line from a to b):
(iii)Thus the integral is independent of path.
The Fundamental Theorem for Divergences
The fundamental theorem for divergences states that: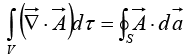
This theorem has at least three special names: Gauss’s theorem, Green’s theorem, or, simply, the divergence theorem. Like the other “fundamental theorems,” it says that the integral of a derivative (in this case the divergence) over a region (in this case a volume) is equal to the value of the function at the boundary (in this case the surface that bounds the volume). Notice that the boundary term is itself an integral (specifically, a surface integral). This is reasonable: the “boundary” of a line is just two end points, but the boundary of a volume is a (closed) surface.
Geometrical Interpretation
If 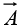 represents the flow of an incompressible fluid, then “the flux of
represents the flow of an incompressible fluid, then “the flux of 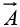 (the right side of equation) is the total amount of fluid passing out through the surface, per unit time and the left side of equation shows an equal amount of liquid will be forced out through the boundaries of the region.
(the right side of equation) is the total amount of fluid passing out through the surface, per unit time and the left side of equation shows an equal amount of liquid will be forced out through the boundaries of the region.
Example 23: Check the divergence theorem using the function 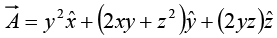 and the unit cube situated at the origin.
and the unit cube situated at the origin.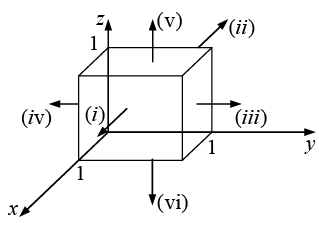
In this case
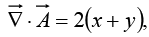
and
Evidently,
To evaluate the surface integral we must consider separately the six sides of the cube:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
So the total flux is:
Example 24: A vector field  is given in spherical coordinates. Evaluate both sides of Divergence Theorem for the volume enclosed between
is given in spherical coordinates. Evaluate both sides of Divergence Theorem for the volume enclosed between
(i) r = 1 and r = 2, and
(ii)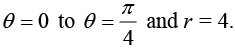
Divergence theorem states that
Since
(i)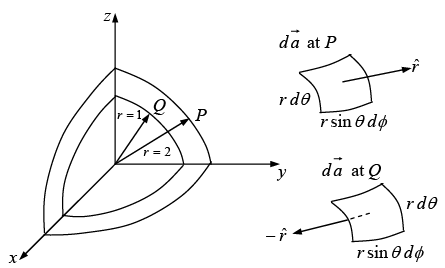
So L.H.S. = R.H.S. = 75π
Divergence theorem proved.
(ii) L.H.S. of Divergence Theorem
R.H.S. of Divergence Theorem
L.H.S. = R.H.S. = 588.91. Divergence theorem proved.
The Fundamental Theorem for Curls
The fundamental theorem for curls, which goes by the special name of Stokes’ theorem, states that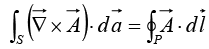
As always, the integral of a derivative (here, the curl) over a region (here, a patch of surface) is equal to the value of the function at the boundary (here, the perimeter of the patch). As in the case of the divergence theorem, the boundary term is itself an integralspecifically, a closed line integral.
Geometrical Interpretation
The integral of the curl over some surface (or, more precisely, the flux of the curl through that surface) represents the “total amount of swirl,” and we can determine that swirl just as well by going around the edge and finding how much the flow is following the boundary (as shown in figure).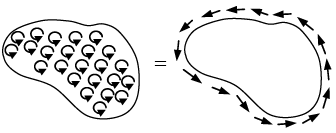
Corollary 1: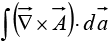 depends only on the boundary line, not on the particular surface used.
depends only on the boundary line, not on the particular surface used.
Corollary 2: 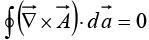 for any closed surface, since the boundary line, like the mouth of a balloon, shrinks down to a point, and hence the right side of equation vanishes.
for any closed surface, since the boundary line, like the mouth of a balloon, shrinks down to a point, and hence the right side of equation vanishes.
Example 25: Suppose 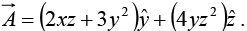 Check Stokes’ theorem for the square surface shown in figure.
Check Stokes’ theorem for the square surface shown in figure.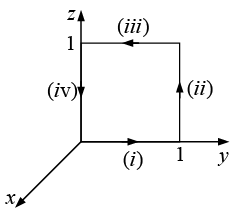
Here
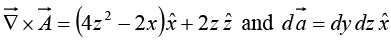
(In saying thatpoints in the x direction, we are chosen to a counterclockwise line integral. We could as well write
but then we have to go clockwise.) Since x = 0 for this surface,
Now, what about the line integral? We must break this up into four segments:
(i)
(ii)
(iii)
(iv)
So
Example 26: Given in cylindrical coordinates. For the contour shown in figure, verify the Stokes’ Theorem.
in cylindrical coordinates. For the contour shown in figure, verify the Stokes’ Theorem.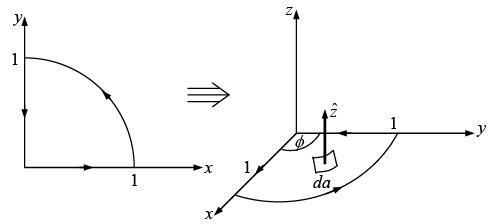
Stokes’ Theorem
In cylindrical coordinates,
Ar = 2r cos∅ , A∅ = r, Az = 0L.H.S. = R.H.S. =
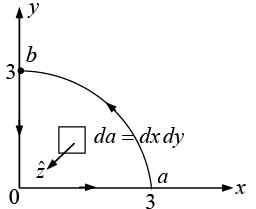
Example 27: Given a vector field 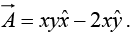 Verify stokes,’ theorem over the path shown in figure.
Verify stokes,’ theorem over the path shown in figure.
Stokes’ theorem
(Equation of quarter circle x2 + y2 = 9; 0 < x, y < 3 )
The Dirac Delta Function
The Divergence of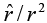
Consider the vector function
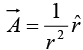
At every location,
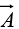 is directed radially outward. When we calculate the divergence we get precisely zero:
is directed radially outward. When we calculate the divergence we get precisely zero: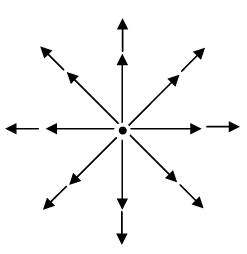
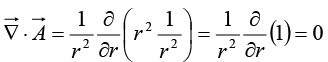
The plot thickens if you apply the divergence theorem to this function. Suppose we integrate over a sphere of radius R, centered at the origin; the surface integral is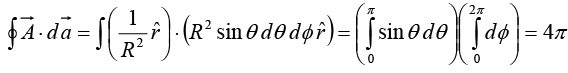
But the volume integral,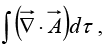 is zero. Does this mean that the divergence theorem is false?
is zero. Does this mean that the divergence theorem is false?
The source of the problem is the point r = 0, where 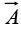 blows up. It is quite true that
blows up. It is quite true that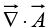 =0 everywhere except the origin, but right at the origin the situation is more complicated.
=0 everywhere except the origin, but right at the origin the situation is more complicated.
Notice that the surface integral is independent of R; if the divergence theorem is right (and it is), we should get 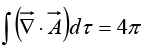 for any sphere centered at the origin, no matter how small. Evidently the entire contribution must be coming from the point r = 0!
for any sphere centered at the origin, no matter how small. Evidently the entire contribution must be coming from the point r = 0!
Thus,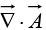 has the bizarre property that it vanishes everywhere except at one point, and yet its integral (over any volume containing that point) is 4π . No ordinary function behaves like that. (On the other hand, a physical example does come to mind: the density (mass per unit volume) of a point particle. It's zero except at the exact location of the particle, and yet its integral is finite namely, the mass of the particle.) What we have stumbled on is a mathematical object known to physicists as the Dirac delta function.
has the bizarre property that it vanishes everywhere except at one point, and yet its integral (over any volume containing that point) is 4π . No ordinary function behaves like that. (On the other hand, a physical example does come to mind: the density (mass per unit volume) of a point particle. It's zero except at the exact location of the particle, and yet its integral is finite namely, the mass of the particle.) What we have stumbled on is a mathematical object known to physicists as the Dirac delta function.
The One- Dimensional Dirac Delta Function
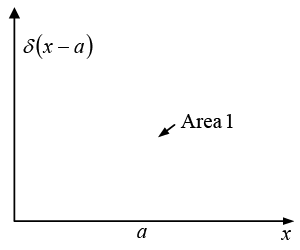
The one dimensional Dirac delta function, δ(x) , can be pictured as an infinitely high, infinitesimally narrow "spike," with area 1 (as shown in figure).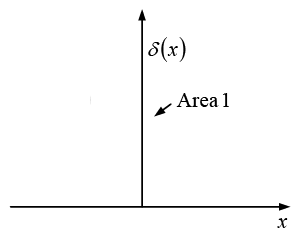
That is to say: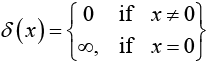
and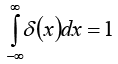
If f (x) is some “ordinary” function then the product f(x)δ(x) is zero everywhere except at x = 0 . It follows that
f(x)δ(x)= f(0)δ(x)
Of course, we can shift the spike from x = 0 to some other point, x = a :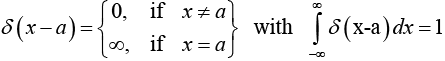
also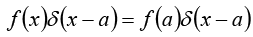
and 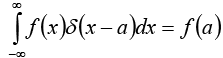
Example 28: Show that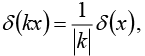
where k is any (nonzero constant). (In particular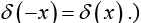
For an arbitrary test function f(x), consider the integral
Changing variables, we let y = kx , so that x = y /kx, andIf k is positive, the integration still runs from -∞ to + ∞ but if k is negative, then x = ∞ implies y = -∞ , and vice versa, so the order of limit is reversed. Restoring the "proper" order costs a minus sign. Thus
(The lower signs apply when k is negative, and we account for this neatly by putting absolute value bars around the final k, as indicated.) Under the integral sign, then, δk(x) serves the same purpose as
Example 29: Evaluate the integral 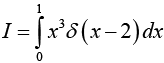
Answer would be 0, because the spike would then be outside the domain of integration.
Example 30: Evaluate the integral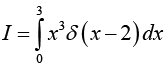
The delta function picks out the value of x3 at the point x = 2 so the integral is 23 = 8 .
Example 31: Show that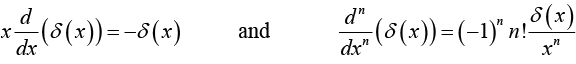
Similarly
Example 32: Let θ (x) be the step function: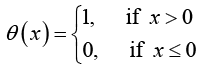
Show that 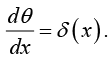
The Three-Dimensional Delta Function
It is an easy matter to generalize the delta function to three dimensions: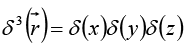
(As always,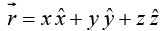 is the position vector, extending from the origin to the point (x, y, z)). This three-dimensional delta function is zero everywhere except at (0, 0, 0), where it blows up. Its volume integral is 1
is the position vector, extending from the origin to the point (x, y, z)). This three-dimensional delta function is zero everywhere except at (0, 0, 0), where it blows up. Its volume integral is 1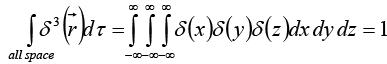
and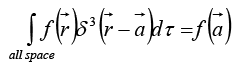
Since the divergence of 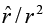 is zero everywhere except at the origin, and yet its integral over any volume containing the origin is a constant ( 4π). These are precisely the defining conditions for the Dirac delta function; evidently
is zero everywhere except at the origin, and yet its integral over any volume containing the origin is a constant ( 4π). These are precisely the defining conditions for the Dirac delta function; evidently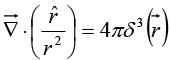
Example 33: Evaluate the integral 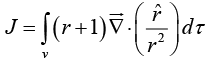 where v is a sphere of radius R centered at the origin.
where v is a sphere of radius R centered at the origin.
The Theory of Vector Fields
If the curl of a vector field 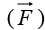 vanishes (everywhere), then
vanishes (everywhere), then 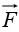 can be written as the gradient of a scalar potential (V):
can be written as the gradient of a scalar potential (V): 
(The minus sign is purely conventional.)
Theorem 1: Curl-less (or "irrotational") fields. The following conditions are equivalent (that is, 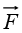 satisfies one if and only if it satisfies all the others):
satisfies one if and only if it satisfies all the others):
(a) 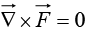 everywhere.
everywhere.
(b) 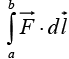 is independent of path, for any given end points.
is independent of path, for any given end points.
(c) 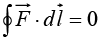 for any closed loop.
for any closed loop.
(d) 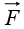 is the gradient of some scalar,
is the gradient of some scalar,
The scalar potential is not unique-any constant can be added to V with impunity, since this will not affect its gradient.
If the divergence of a vector field 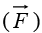 vanishes (everywhere), then
vanishes (everywhere), then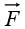 can be expressed as the curl of a vector potential
can be expressed as the curl of a vector potential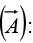
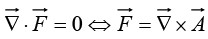
That’s the main conclusion of the following theorem:
Theorem 2: Divergence-less (or “solenoidal”) fields. The following conditions are equivalent:
(a) everywhere.
everywhere.
(b)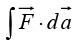 is independent of surface, for any given boundary line.
is independent of surface, for any given boundary line.
(c)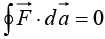 for any closed surface.
for any closed surface.
(d) 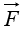 is the curl of some vector,
is the curl of some vector,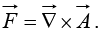
The vector potential is not unique-the gradient of any scalar function can be added to  without affecting the curl, since the curl of a gradient is zero.
without affecting the curl, since the curl of a gradient is zero.
|
78 videos|18 docs|24 tests
|
FAQs on Fundamental Theorems & Dirac Delta Function - Mathematical Methods - Physics
| 1. What is the Dirac Delta function? |  |
| 2. What are the applications of the Dirac Delta function? |  |
| 3. How is the Dirac Delta function defined mathematically? |  |
| 4. What are the properties of the Dirac Delta function? |  |
| 5. Is the Dirac Delta function a real function? |  |