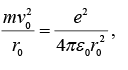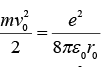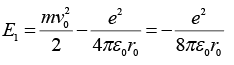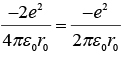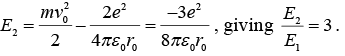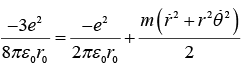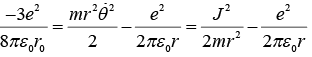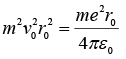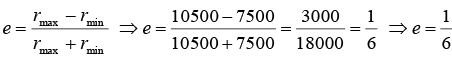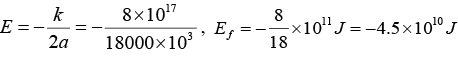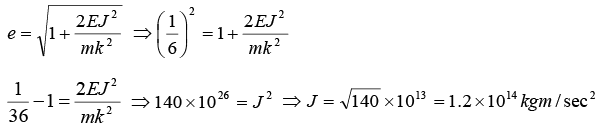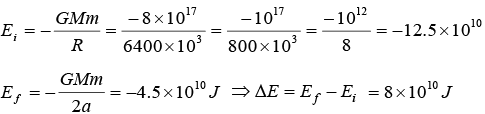Kepler’s System | Mechanics & General Properties of Matter - Physics PDF Download
Kepler’s Potential
The Kepler’s potential is given by V (r) = -k/r with k > 0 which is central potential. If Particle of mass m and angular momentum J is interact with potential, then effective potential is given Veffective =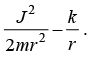
If one will plot Veffective against r
Analysis of Veffective 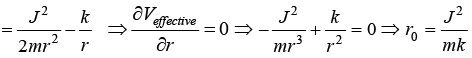
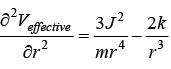 the value of
the value of 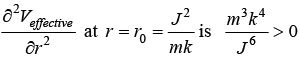 which is minima of the Veffective.
which is minima of the Veffective.
The Analysis of Veffective for Kepler’s law
Case: 1 for r = r0 = J2/mk total energy E0 = - mk2/2j2 he motion of path is elliptical
Case: 2 E0 <E< 0 the particle is bounded between turning point a <r< b and the motion is equivalent to small oscillation about stable point r = r0 and shape of orbit is elliptical in nature.
Case: 3 E = 0 the particle is unbounded where r = c is turning point.
Case: 4 E > 0 the particle is unbounded where r = d is turning point.
Equation of orbit for Kepler’s
Equation of motion is given by 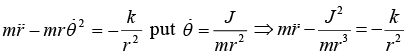
Equation of orbit is given by 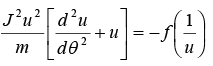
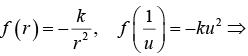
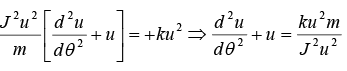
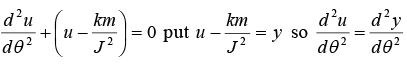
The equation reduce to d2y/dθ2 + y = 0
The solution of equation reduce to y = A cosθ u - km/J2 = A cos θ ⇒ u = km/J2 + A cos θ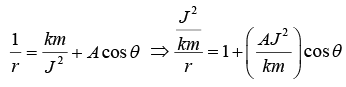
Put l km J2/km = l and e = AJ2/km, then equation reduce to l/r = 1 + e cos θ, which is equation of conics where l is latus rectum and e is eccentricity.
In a central force potential which is interacting with potential V (r) = -k/r can be any conics
section depending on eccentricity e.
Relationship between Energy and Eccentricity
For central potential V(r) = -k/r, the solution of orbit is l/r = 1 + e cos θ with l = j2/km
The energy is given by E = 1/2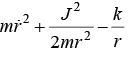
The solution of orbit is 1/r = 1 +e cos θ with l = j2/km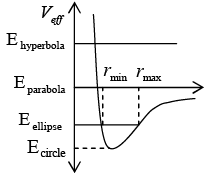 So
So 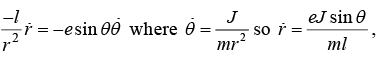
After putting the value of l/r = 1 + e cos θ and 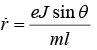 with l = j2/km in equation of energy, one will get e =
with l = j2/km in equation of energy, one will get e =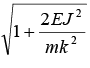
the condition on energy for possible nature of orbit for potential
E > 0 e > 1 Hyperbola
E = 0 e = 1 Parabols
E < 0 e< 1 Ellipse
E = -mk2/2J2 e = 0 Circle
Two Body Problem
Reduction of two body central force problem to the equivalent one body problem.
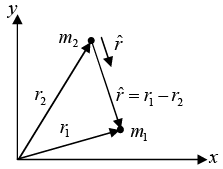
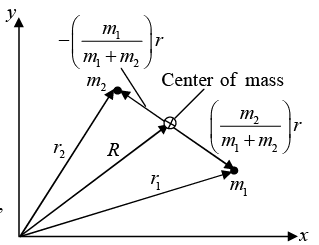
A system of two particles of mass m1 and m2 whose instantaneous position vectors of inertial frame with origin O are r1 and r2 respectively.
Vector m2 relative to m1 is 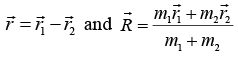
Central Force Motion as a One Body Problem
Consider an isolated system consisting of two particles interacting under a central force f(r). The masses of the particles are m1 and m2 and their position vectors are r1 and r2. We have
r = r1 - r2 ⇒ r = |r| = |r1 - r2|
The equations of motion are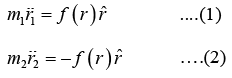
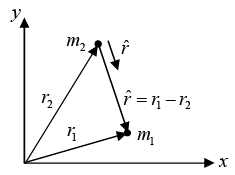 The force is attractive for f (r) < 0 and repulsive for f (r) > 0 .Above equation are coupled Equations are coupled together by r ; the behavior of r1 and r2 depends on r = r1 - r2. To find the equation of motion for r we divide equation by m1 (1) and equation by m2 (2) and subtract.
The force is attractive for f (r) < 0 and repulsive for f (r) > 0 .Above equation are coupled Equations are coupled together by r ; the behavior of r1 and r2 depends on r = r1 - r2. To find the equation of motion for r we divide equation by m1 (1) and equation by m2 (2) and subtract.
This gives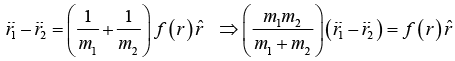
Where 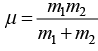 is identified as reduce mass and equation of motion is written in form of reduced mass as
is identified as reduce mass and equation of motion is written in form of reduced mass as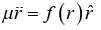 system can be shown as given in figure.
system can be shown as given in figure.
Equation is identical to the equation of the motion for a particle of mass µ acted on by a force  ; no trace of the two particle problem remains.
; no trace of the two particle problem remains.
The two particle problem has been transformed to a one particle problem.
Transformation of two body on center of mass reference frame and calculation of energy
We shall show that the problem is easier to handle if we replace r1 and r2 by r = r1 - r2 and the center of mass vector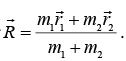 The equation of motion for R is trivial since there are no external forces. The equation for r turns out to be like the equation of motion of a single particle and has a straight forward solution.
The equation of motion for R is trivial since there are no external forces. The equation for r turns out to be like the equation of motion of a single particle and has a straight forward solution.
The equation of motion for R is 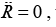 , which has the simple solution R = R0 + vt
, which has the simple solution R = R0 + vt
The constant vectors R0 and v depend on the choice of coordinate system and the initial conditions. If we are clever enough to take the origin at the center of mass, R0 = 0 and v = 0.
Solving for r1 and r2 gives
For a simple trick lets fixed center of mass at origin ie for put R = 0
Total energy of system is given by
Put value of 
The energy of system is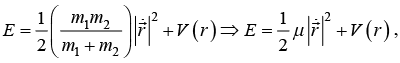
where μ = 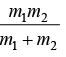 is identified as reduced mass.
is identified as reduced mass.
Hence V (r) is central potential so motion is then motion is confided in the plane 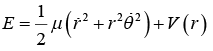
Kepler’s Law
Kepler discuss the orbital motion of the sun and Earth system under the potential, V(r) = -k/r where k = Gmsme, it is given ms and me is mass of Sun and Earth. Although Kepler discuss sun and earth system but method can be used for any system which is interacting with potential V(r) = - k/r
The reduce mass for sun and earth system is µ = 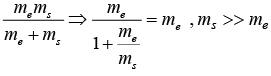
Let us assume mass of earth me = m
Kepler’s First Law
Every planet (earth) moves in an elliptical orbit around the sun, the sun is being at one of the foci. Where sun and earth interact each other with potential V(r) = k/r We solve equation of motion in center of mass reference frame with reduce mass μ = me = m
Equation of Motion
Now, we discuss the case specially of elliptical orbit as Kepler discuss for planetary motion.
Total energy, E = 1/2 mr2 + J2/2m2 - k/r where Veffective = J2/2mr2 - k/r with constant angular momentum J.
If one will plot Veffective vs r , it is clear that for negative energy the orbit is elliptical which is shown in figure.
Earth is orbiting in elliptical path with sun as focus as shown in figure.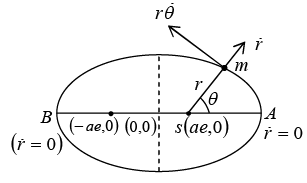 Let equation of this ellipse is
Let equation of this ellipse is 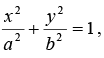
where b = 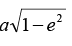
Minimum value of r is (a - ae) and maximum value of r is (a + ae), rmax + rmin = 2a.
From plot of effective potential, it is identified rmax and rmin is the turning point, so at these points radial velocity is zero.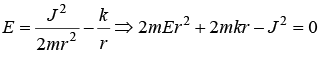 given equation is quadratic in term of r, for their root at rmax and rmin. Using theory of quadratic equation sum of root, rmax + rmin = -2mk/2mE
given equation is quadratic in term of r, for their root at rmax and rmin. Using theory of quadratic equation sum of root, rmax + rmin = -2mk/2mE
⇒ E = -k/2α, which is negative.
Kepler’s Second Law
Equal Area will swept in equal time or Areal velocity is constant.
dA/dt = J/2m = (which is derived earlier)
Kepler’s Third Law
The square of time period (T) of revolution in elliptical orbit is proportional to cube of semi major axis a i.e., T2 ∝ a3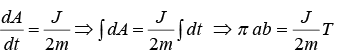 (πab is the area of ellipse)
(πab is the area of ellipse)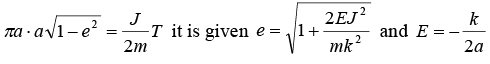
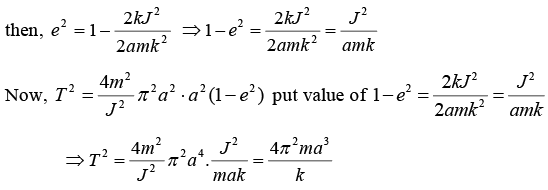
If k = Gmsm then ⇒ T2 = 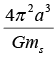 where ms is mass of the Sun.
where ms is mass of the Sun.
Example 4: Given a classical model of tritium atom with nucleus of charge +1 and a single electron in a circular orbit of radius r0, suddenly the nucleus emits a negatron and changes to charge +2 (the emitted negatron escapes rapidly and we can forget about it) the orbit suddenly has a new situation.
(a) Find the ratio of the electron’s energy after to before the emission of the negatron
(b) Describe qualitatively the new orbit
(c) Find the distance of closest and the farthest approach for the new orbits in units of r0
(a) As the negatron leaves the system rapidly, we can assume that its leaving has no effect on the position and kinetic energy of the orbiting electron.
From the force relation for the electron,
And we find its kinetic energy
And its total mechanical energy,
Before the emission of the negatron. After the emission the kinetic energy of the electron is stillwhile its potential energy suddenly changes to
Thus after the emission the total mechanical energy of the orbiting electron is
In other words, the total energy of the orbiting electron after the emission is three times as large as that before the emission.
(b) As E2 =the condition for circular motion is no longer satisfied and the new orbit is an ellipse.
(c) Conservation of energy gives
At positions where the orbiting electron is at the distance of closest or farthest approach to the atom, we have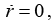
for which
Then with, j2 =
The above becomes 3r2 - 4r0r+ r02 = 0 with solutions r = r0/3 = r = r0
Hence the distances of closest and farthest approach in the new orbit are respectively
rmin = 1/3, rmax = 1
Example 5: A satellite of mass m = 2000 kg is in elliptical orbit about earth. At perigee it has an altitude of 1,100 km and at apogee it has altitude 4,100 km. assume radius of the earth is Re = 6, 400 km. it is given GmMe = 8 × 1017 j m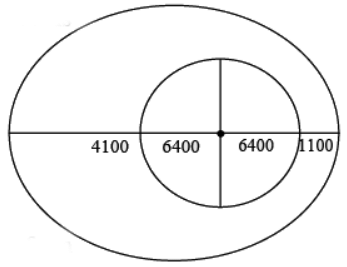 (a) What is major axis of the orbit?
(a) What is major axis of the orbit?
(b) What is eccentricity of the orbit?
(c) What is angular momentum of the satellite?
(d) How much energy is needed to fix satellite in to orbit from surface of earth?
rmax = 4100 + 6400 = 10500 km
rmin= 1100 + 6400 = 7500km
(a) rmax + rmin = 2α ⇒ 18000 = 2a ⇒ a = 9000km
(b)
It is given k = 8 × 1017 J.m
(c)
(d) When satellite is at surface of earth,
R = 6400 Km
Example 6: For circular and parabolic orbits in an attractive 1/r potential having the same angular momentum, show that perihelion distance of the parabola is one-half the radius of the circle.
For Kepler’s problem, l/r = 1 + e cos θ, for circular orbit e = 0 ⇒ l/rc = 1
And for parabola e = 1, l/rp = 1 + cos θ, rp is minimum when cosθ is maximum
Example 7: A planet of mass m moves in the inverse square central force field of the Sun of mass M . If the semi-major and semi-minor axes of the orbit are a and b , respectively, the find total energy of the planet by assuming sun is at center of ellipse.
Assume Sun is at the centre of elliptical orbit.
Conservation of energy
Conservation of momentum L =mv1a= mv2b
|
61 videos|23 docs|25 tests
|
FAQs on Kepler’s System - Mechanics & General Properties of Matter - Physics
| 1. What is Kepler's potential? |  |
| 2. What is the significance of Kepler's potential in the Two Body Problem? |  |
| 3. How does Kepler's System relate to Kepler's potential? |  |
| 4. Can Kepler's potential be applied to other celestial objects apart from planets? |  |
| 5. How does Kepler's potential contribute to understanding the stability of planetary systems? |  |