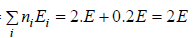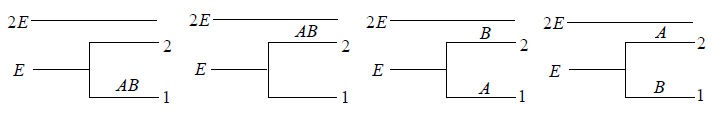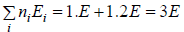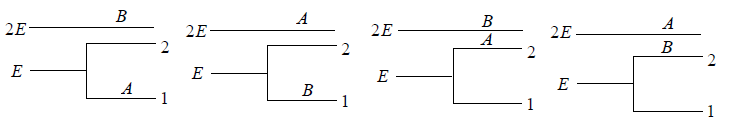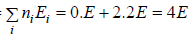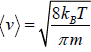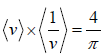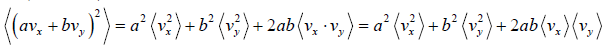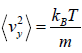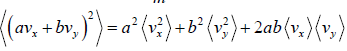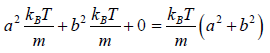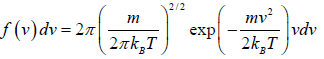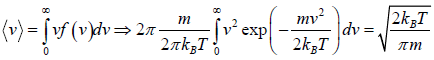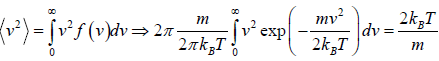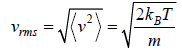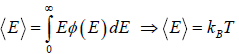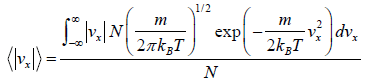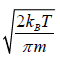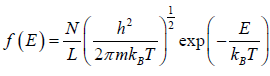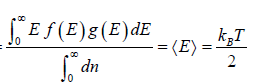Maxwell-Boltzmann Distribution | Kinetic Theory & Thermodynamics - Physics PDF Download
Introduction
In statistical mechanics, the Maxwell–Boltzmann distribution describes particle speeds in gases, where the particles move freely without interacting with one another, except for very brief elastic collision in which they may exchange momentum and kinetic energy, but do not change their respective states of intermolecular excitation, as a function of the temperature of the system, the mass of the particle, and speed of the particle. Particle in this context refers to the gaseous atoms or molecules – no difference is made between the two in its development and result.
Maxwell –Boltzmann system constituent identical particles that are distinguishable in nature which means we can distinguish them by name, color, put any number or any level on particle
For example, if we want to identify two distinguishable particles, we can say that first particle is A and second particle is B . In another way, we can also identify the colour of particles as red for first particle and black for second particle. There is no any restriction on number of particles which can occupy any energy level.
Quantum mechanically, the wave function of particle will not overlap to each other because mean separation of particles is more than the thermal wavelength, which is identified by λ. (where λ = 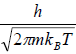 is defined as the thermal wavelength)
is defined as the thermal wavelength)
Number of ways (W) that ni number of distinguishable particle which can be adjusted in gi number of quantum is 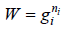
Suppose there are states with energies E1,E2,E3,.....El and degeneracy of each state g1, g2, g3,......gl respectively the ith level can be shown schematically
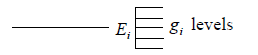
If there is N numbers of distinguishable particles out of these n1, n2, n3,....nl particles is adjusted in energy level E1,E2,E3,.....El respectively.
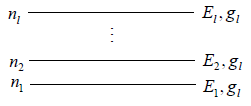
Total number of particle is constant n1+ n2+ n3+,....+nl = N, 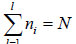
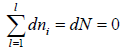
Total energy of configuration is constant n1E1+ n2E2+,.... 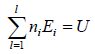
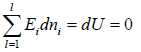
Now, number of ways selecting n1 out of N particles then distribute it in energy state E1 which degeneracy is g1 then 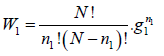
The total number W of distinct ways of obtaining the distribution of n1, n2, n3,....nl particles among the energy states E1,E2,E3,.....El
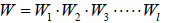
W = 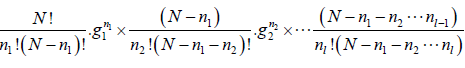
= 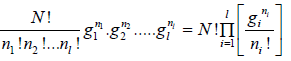
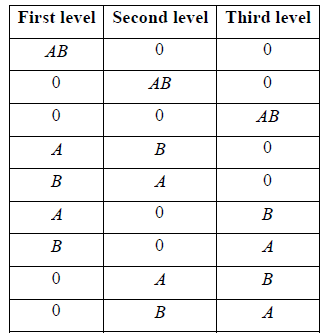
Example 13: Two distinguishable particles have to be adjusted in a state whose degeneracy is three
(a) How many ways the particles can be adjusted?
(b) Show all arrangement.
(a) N = 2,n = 2, g = 3 and number of microstate is W =
.
(b) Total number of arrangement for 2 distinguishable in state whose degeneracy is 3.
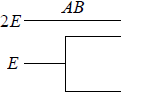
Example 14: If two distinguishable particle have to adjusted in two quantum level with ground state energy E and first excited state having energy 2E having degeneracy 1 and 2.
(a) What will number of ways that total energy of distribution is 2E i.e. both the particles in ground state.
(b) What will number of ways that total energy of distribution is 3E i.e., one the particle in ground state and other in first excited state .
(c) What will number of ways that total energy of distribution is 4e i.e. both the particle in first excited state.
(a) N = 2, g1 = 2, g2 = 1, n1 = 2, n2 = 0 total energy U =
W =
= 4 given distribution is shown in figure.
(b) N = 2, g1 = 2, g2 = 1, n1 = 1, n2 = 1 total energy U =
W =
= 4 given distribution is shown in figure.
(c) N = 2, g1 = 2, g2 = 1, n1 = 1, n2 = 1 total energy U =
W =
= 1 the given distribution is shown in figure
Energy distribution of Ideal gas in three dimension
Entropy (S) is measurement of randomness of system. It is function of number of microstate (which is number of ways to achieve any energy (E). Statistically it is seen so 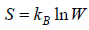 . And Law of nature reveal that at equilibrium the entropy is maximum so
. And Law of nature reveal that at equilibrium the entropy is maximum so 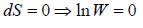
For distinguishable particle. Taking in for equation W = 
Using sterling approximation 
= 
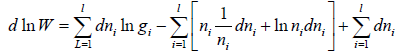
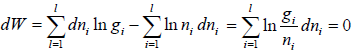
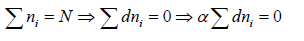
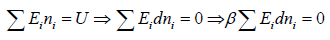
where α and β are used as LaGrange’s multiplier which is using to make equation dimensionless where dimension of β is inverse of energy can be related to equilibrium
temperature T so 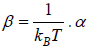 can be identified later can be related to fugacity
can be identified later can be related to fugacity
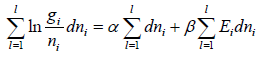
Equating the coefficient of dni then 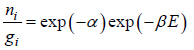
So, Maxwell distribution is given by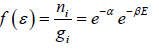
Calculation of α in three dimensional case
Total number of particles in ideal gas N = 
where energy levels are continuous then N = 
for three dimensional case g (E) = 
N = 
N = 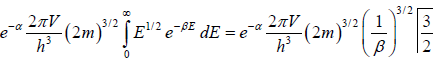
where β = 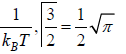
Derivation of Maxwell-Boltzmann Distribution in three dimension
The Maxwell-Boltzmann distribution law for the particles in the states is
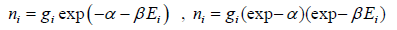
After using the values 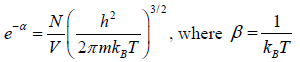
We get 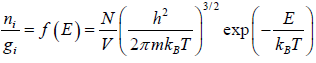
The number of particles dN(E) having energies in the range from E to E +dE is dN(E) = f (E)g(E)dE where f (E) is distribution function and g(E)dE is number of level (quantum state) in the range of E to E + dE
The number of particles dn(E) having energies in the range from E to E + dE in three dimensional space
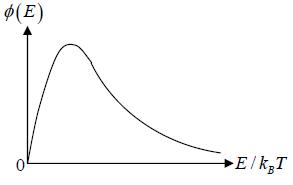
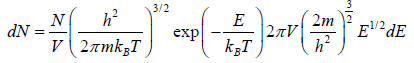
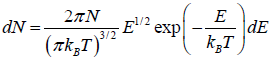
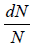 is fraction of particles that have energy between from E to E + dE is
is fraction of particles that have energy between from E to E + dE is
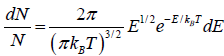 which is popularly known as probability to find gas have energy between from E to E + dE
which is popularly known as probability to find gas have energy between from E to E + dE 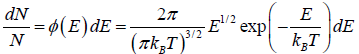 , where
, where 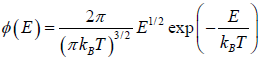 is identified probability density.
is identified probability density.
This is known as the Maxwell-Boltzmann energy distribution law for an ideal gas, where λ = 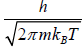 is defined as the thermal wavelength.
is defined as the thermal wavelength.
Average Energy, Root mean square and most probable energy in three dimensional system.
For the Maxwell-Boltzmann energy distribution law, average energy (E) of the particles is
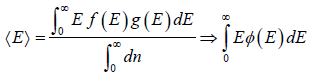
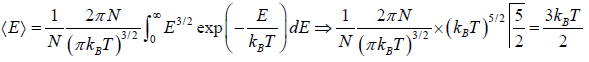
Hence, the average of a particle is 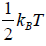 per degree of freedom, for three degree of freedom it is
per degree of freedom, for three degree of freedom it is 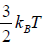
Mean square of energy (E2) = 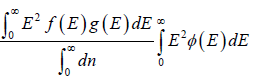
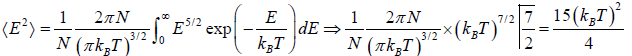
Root mean Energy 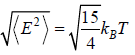
Most probable Energy
Probability density  then The most probable energy is given by
then The most probable energy is given by 
Energy distribution in different dimension
 distribution function in three dimension, where V is the volume
distribution function in three dimension, where V is the volume distribution function in two dimension, where A is area.
distribution function in two dimension, where A is area.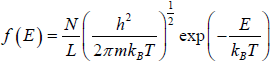 distribution function in one dimension, where L is length.
distribution function in one dimension, where L is length.
Maxwell-Boltzmann Distribution Law Distribution of Molecular Velocity in perfect gas
Maxwell-Boltzmann distribution law is applicable for ideal gas, where molecules have no vibrational or rotational energies.
In the equilibrium state of the molecules, molecules have completed their random motion and probability that a molecule has a given velocity component is independent of other two components.
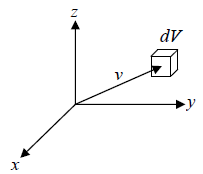
In the given figure dv is volume element in velocity space for a molecule at velocity 
We need to calculate number of molecules simultaneously having component in the range 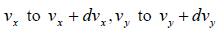 and
and 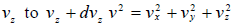 , which is equation of sphere and dvxdvydvz can be replaced by
, which is equation of sphere and dvxdvydvz can be replaced by 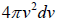 . There is an assumption in Maxwell-Boltzmann distribution law that probability that a molecule selected at random has velocities in a given range is a purely function of the magnitude of velocity and the width of the interval.
. There is an assumption in Maxwell-Boltzmann distribution law that probability that a molecule selected at random has velocities in a given range is a purely function of the magnitude of velocity and the width of the interval.
The Distribution in Terms of Magnitude
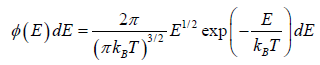
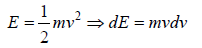
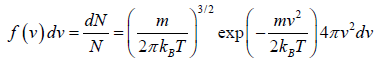
We need to calculate number of molecules simultaneously having component in the range 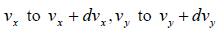 and
and 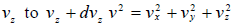 which is equation of sphere and
which is equation of sphere and 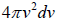 can be replaced by dvxdvydvz .
can be replaced by dvxdvydvz .
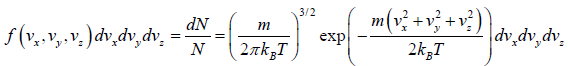
where 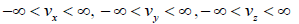
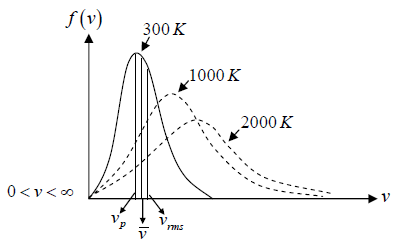
Average Speed
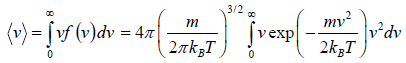
= 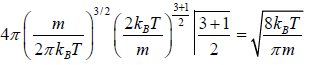
Mean square Speed
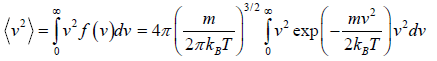
= 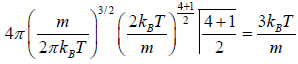
Root Mean Square speed
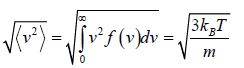
Most probable speed
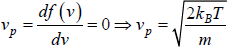
Average velocity of 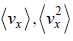
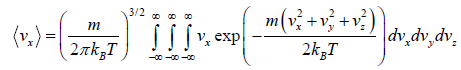 = 0
= 0
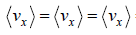 = 0
= 0
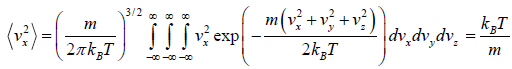
Similarly, 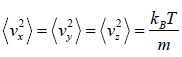
Example 15: For Maxwellian gas, find the 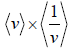
As,
=
⇒
Example 16: If vx and are vy are x and y component of velocity then find the average value of 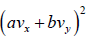
Similarly, (vy) = 0 and
Therefore,
=
Example 17: (a) Write down expression of Maxwell distribution function for speed in two dimensional in equilibrium temperature T
(b) Find Average speed for two dimensions in two dimensional at equilibrium temperature T
(c) Find RMS speed for two dimensions in two dimensional at equilibrium temperature T
(d) Write down expression of Maxwell distribution function for energy in two dimensional at equilibrium temperature T
(e) Find average energy for two-dimensional system at equilibrium temperature T.
(a)
(b)
(c)
,
⇒
; 0 < E < ∞
(d)
Example 18: Using the Maxwell distribution function, calculate the mean velocity
projection vx and the mean value of the modulus of this projection 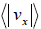 , if the mass of each molecule is equal to m and the gas temperature is T.
, if the mass of each molecule is equal to m and the gas temperature is T.
We know that Mean Velocity
= 0
Mean speed,
=
Example 19: If N number of distinguishable particle is kept into one dimensional box of length L. What is average energy at temperature T .
for two dimensional system g(E)dE =
and distribution Function is given by
(E) =
|
6 videos|20 docs|32 tests
|
FAQs on Maxwell-Boltzmann Distribution - Kinetic Theory & Thermodynamics - Physics
| 1. What is the Maxwell-Boltzmann distribution in three dimensions? |  |
| 2. How is the energy distribution different in different dimensions? |  |
| 3. What is the significance of the Maxwell-Boltzmann distribution in IIT JAM? |  |
| 4. How is the molecular velocity distributed in a perfect gas according to the Maxwell-Boltzmann distribution? |  |
| 5. What are some common misconceptions about the Maxwell-Boltzmann distribution? |  |