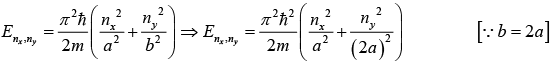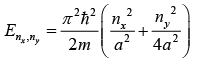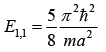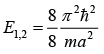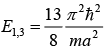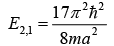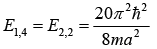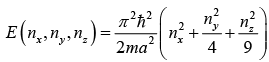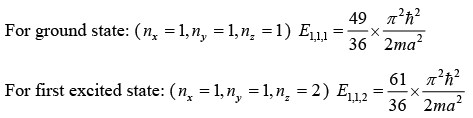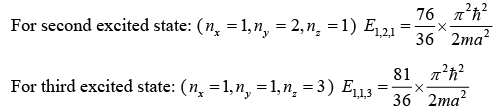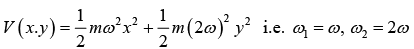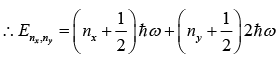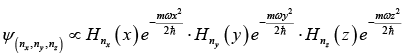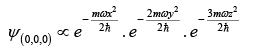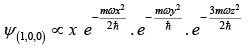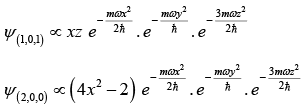Multiple Dimensional Systems | Modern Physics PDF Download
| Table of contents |

|
| Two Dimensional Free Particle |

|
| Particle in Two Dimensional Box |

|
| Particle in Three Dimensional Box |

|
| Two Dimensional Harmonic Oscillator |

|
| Three Dimensional Harmonic Oscillators |

|
If x, y, z are independent, then ψ(x, y, z) can be written as X(x) Y(y) Z(z) and Energy Eigen value can be written as Ex,y,z = Ex + Ey + Ez
Where, HxX(x) = ExX(x), HyY(y) = EyY(y), HzZ(z) = EzZ(z)
and H = Hx + Hy + Hz and Hψ = E(ψ)
Two Dimensional Free Particle
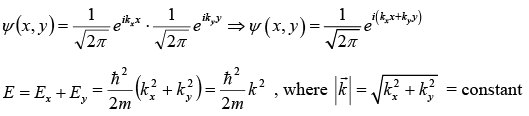
So, two dimensional free particle is infinitely degenerate.
Three Dimensional Free Particle
The wave function is ψ(x, y, z) is defined as
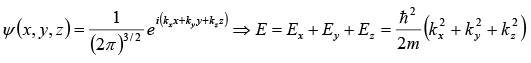
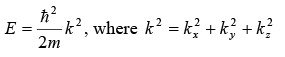
So, three dimensional free particle is infinitely degenerate.
Particle in Two Dimensional Box
The two dimensional system is defined as,
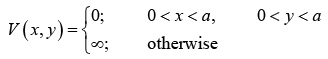
The wave function is given as
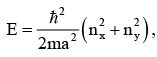 where nx = 1, 2, 3..... and 1, 2, 3,......
where nx = 1, 2, 3..... and 1, 2, 3,......
Ground state energy (nx = 1, ny = 1) i.e.,
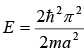
First excited state (nx = 1, ny = 2) i.e.,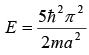
(Degeneracy of first excited state is doubly degenerate)
Second excited state nx = 2, ny = 2,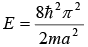
Third excited state nx = 1, ny = 3,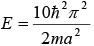
(Third excited state is doubly generated)
Particle in Three Dimensional Box
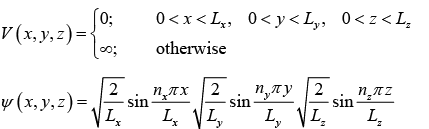
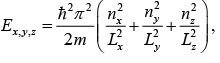
where nx = 1,2,3, ..... ny = 1, 2, 3, .....
For cubic box Lx = Ly = Lz = L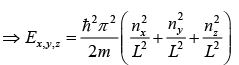
Where, nx = 1, 2, 3, ...., ny = 1, 2, 3, ..., nz = 1, 2, 3, ....
Ground state energy (nx = 1, ny = 1, nz = 1) i.e.,
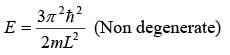
First excited state energy (nx = 1, ny = 1, nz = 2) i.e.,
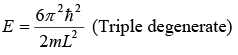
Other configurations are, nx = 1, ny = 2, nz = 1 and nx = 2, ny = 1, nz = 1
Second excited state energy (nx = 2, ny = 2, nz = 1) i.e.,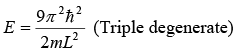
Other configurations are, nx = 2, ny = 1, nz = 2 and nx = 1, ny = 2, nz = 2
Two Dimensional Harmonic Oscillator
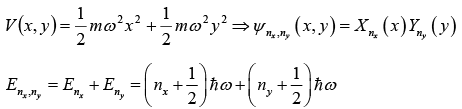
= (nx + ny + 1)ℏω, where nx 0,1, 2, 3, ..... and ny = 0,1, 2, 3, .....
= (n + 1)ℏω, where n = 0,1, 2, 3, ........
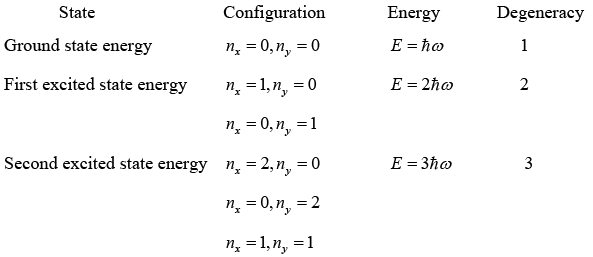 So, degeneracy of two dimensional harmonic oscillators for nth state is (n +1)
So, degeneracy of two dimensional harmonic oscillators for nth state is (n +1)
Three Dimensional Harmonic Oscillators
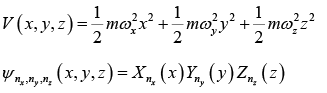
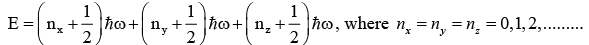
For isotropic harmonic oscillator, ωx = ωy = ωz 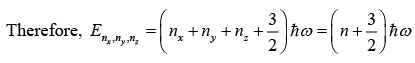
The degeneracy of the isotropic harmonic oscillator for nth state is, gn = 1/2 (n + 1)(n + 2)
Where, n = 0 corresponds to ground state.
Example: If b = 2a , write down ground, first, second and third excited state energy.
For ground state:
For first excited state:
For second excited state:
For third excited state:
For fourth excited state:
Example:

If b = 2a and c = 3a, then write down energy eigenvalue for ground state, first excited state and second excited state.
Example: If the potential of two dimensional harmonic oscillator is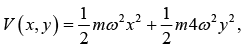 then find energy Eigen value.
then find energy Eigen value.
For ground state: E0,0 = 3/2 ℏω
For first excited state: E1,0 = 5/2 ℏω
For second excited state: E0,1 = E2,0 = 7/2 ℏω (Doubly degenerate)For third excited state: E3,0 = 9/2 ℏω
For fourth excited state: E2,1 = E4,0 = 11/2 ℏω (Doubly degenerate)
Example: If the potential of three dimensional harmonic oscillator is,
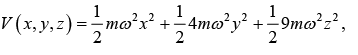
then write down unnormalised wavefunction for ground state, first excited state and second excited state.
Wave function
For ground state: (nx, ny, nz) then wave function
For first excited state: (nx, ny, nz) = (1, 0, 0) then wave functionFor second excited state: (nx, ny, nz) = (1, 1,0), (2,0,0), then wave function
|
37 videos|17 docs|19 tests
|