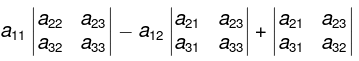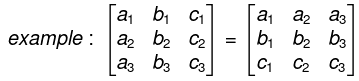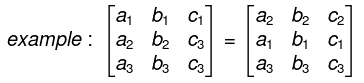Matrices and Determinants- 1 | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Matrices |

|
| Algebra of a Matrix |

|
| Rank of Matrix |

|
| Inverse of a Matrix |

|
| Determinants |

|
Matrices
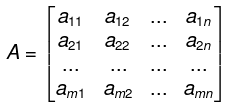
- A matrix A over a field K or, simply, a matrix A (when K is implicit) is a rectangular array of scalars usually presented in the following form:

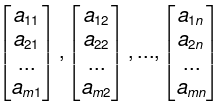
- The rows of such a matrix A are the m horizontal lists of scalars:
(a11, a12, ..., a1n), (a21, a22, ..., a2n), ... , (am1, am2, ..., amn)
and the columns of A are the n vertical lists of scalars:
Note that the element aij, called the ij-entry or ij-element, appears in now i and column j. - We frequently denote such a matrix by simply writing A = [aij].
- Two matrices A and B are equal, written A = B, if they have the same size and if corresponding elements are equal. Thus the equality of two m x n matrices is equivalent to a system of mn equalities, one for each corresponding pair of elemen
Algebra of a Matrix
1. Matrix Addition and Multiplication
- Let A = [aij]and B = [bij] be two matrices with the same size , say m x n matrices. The sum of A and B, written A + B, is the matrix obtained by adding corresponding elements from A and B. That is,

- The product of the matrix A by a scalar k, written k . A or simply kA, is the matrix obtained by multiplying each element of A by k. That is,

Observe that A + B and kA are also m x n matrices. We also define
-A= (-1) A and A - B = A + (-B) - The matrix - A is called the negative of the matrix A, and the matrix A - B is called the difference of A and B. The sum of matrices with different sizes is not defined.
- Example:
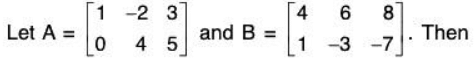


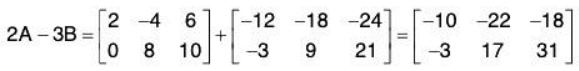
The matrix 2A - 3B is called a linear combination of A and B.
Basic properties of matrices under the operations of matrix addition and scalar multiplication follows.
Consider any matrices A, B, C (with the same size) and any scalars k and k’. Then:
(i) (A + B) + C = A + (B + C ),
(ii) A + 0 = 0 + A = A,
(iii) A + (- A) = (- A) + A = 0,
(iv) A + B = B + A,
(v) k(A + B) = kA + kB,
(vi) (k + k’)A = kA + k’A,
(vii) (k k’)A = k (k’A),
(viii) 1· A = A.
2. Matrix Multiplication
- The product of matrices A and B, written AB, is somewhat complicated. For this reason, we first begin with a special case.
- The product AB of a row matrix A = [aj] and a column matrix B = [bj] with the same number of elements is defined to be the scalar (or 1 x 1 matrix) obtained by multiplying corresponding entries and adding; that is,
 We emphasize that AB is a scalar (or a 1 x 1 matrix). The product AB is not defined when A and B have different numbers of elements.
We emphasize that AB is a scalar (or a 1 x 1 matrix). The product AB is not defined when A and B have different numbers of elements. - Example:

3. Product of Matrices
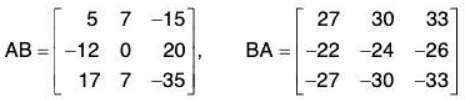
- Suppose A = [aik] and B = [bkj] are matrices such that the number of columns of A is equal to the number of rows of B; say, A is an m x p matrix and B is a p x n matrix. Then the product AB is the m x n matrix whose ij-entry is obtained by multiplying the ith row of A by the jth column of B. That is,
 where
where
- The product AB is not defined if A is an m x p matrix and B is a q x n matrix, where p is not equal to q.
Let A, B, C be matrices. Then,
(i) (AB)C = A(BC) (associative law),
(ii) A(B + C) = AB + AC (left distributive law),
(iii) (B + C)A = BA + CA (right distributive law),
(iv) k(AB) = (kA)B = A(kB), where k is a scalar.
We note that OA = 0 and BO = 0, where 0 is the zero matrix.
4. Transpose of a Matrix
- The transpose of a matrix A, written AT, is the matrix obtained by writing the columns of A, in order, as rows. For example,
 In other words, if A = [aij] is an m x n matrix, then AT = [bij] is the n x m matrix where bij = aji.
In other words, if A = [aij] is an m x n matrix, then AT = [bij] is the n x m matrix where bij = aji. - Observe that the transpose of a row vector is a column vector. Similarly, the transpose of a column vector is a row vector.
The next theorem lists basis properties of the transpose operation. - If A and B be matrices and let k be a scalar. Then, whenever the sum and product are defined:
(i) (A + B)T = AT + BT,
(ii) (AT)T = A,
(iii) (kA)T = kAT,
(iv) (AB)T = BTAT.
5. Square Matrices
- A square matrix is a matrix with the same number of rows as columns. An n x n square matrix is said to be of order n and is sometimes called an n-square matrix.
- Example:The following are square matrices of order 3.

The following are also matrices of order 3:

6. Diagonal and Trace
- Let A = [ aij] be an n-square matrix. The diagonal or main diagonal of A consists of the elements with the same subscripts, that is,
a11, a22, a33, ... ann - The trace of A, written tr(A), is the sum of the diagonal elements. Namely,
tr(A) = a11+ a22+ a33+ ...+ ann - The following theorem applies.
Suppose A = [aij] and B = [bij] are n-square matrices and k is a scalar. Then,
(i) tr(A + B) = tr(A) + tr(B),
(ii) tr(kA) = k tr(A),
(iii) tr(AT) = tr(A),
(iv) tr(AB) = tr(BA).
- Example:
Let
Then
diagonal of A = {1, -4, 7} and tr(A) = 1 - 4 + 7 = 4
diagonal of B = {2, 3, -4} and tr(B) = 2 + 3 - 4 = 1
Moreover,
tr(A + B ) = 3 - 1 + 3 = 5.
tr(2A) = 2 - 8 + 14 = 8.
tr(AT) = 1 -4 + 7 = 4
tr(AB) = 5 + 0 - 35 = -30,
tr(BA) = 27 - 24 - 33 = -30
As expected from the theorem,
tr(A + B) = tr(A) + tr(B),
tr(AT) = tr(A), tr(2A) = 2 tr(A) - Furthermore, although AB x BA, the traces are equal.
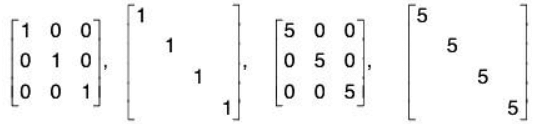
7. Identity Matrix, Scalar Matrices
- The n-square identity or unit matrix, denoted by ln, or simply I, is the n-square matrix with 1’s on the diagonal and 0's elsewhere. The identity matrix I is similar to the scalar 1 in that, for any n-square matrix A,
Al = IA = A - More generally, if B is an m x n matrix, then Bln = lmB = B.
- For any scalar k, the matrix kl that contains k’s on the diagonal and 0's elsewhere is called the scalar matrix corresponding to the scalar k.
- Observe that
(kl)A = k(IA) = kA - That is, multiplying a matrix A by the scalar matrix kl is equivalent to multiplying A by the scalar k.
- Example: The following are the identity matrices of orders 3 and 4 and the corresponding scalar matrices for k = 5;

Remark 1: It is common practice to omit blocks or patterns of 0's when there is no ambiguity, as in the above second and fourth matrices.
Remark 2: The Kronecker delta function δij is defined by
Thus the identity matrix may be defined by I = [δij]
8. Power of Matrices, Polynomials in Matrices
- Let A be an n-square matrix over a field K. Powers of A are defined as follows:
A2 = AA, A3 = A2A, ... , An+1 = An A, ...., and A0 = I - Polynomials in the matrix A are also defined. Specifically, for any polynomial
f(x) = a0 + a1x + a2x2 +...+ anxn ,where the ai are scalars in K, - f(A) is defined to be the following matrix: f(x) = a0I + a1A + a2A2 +...+ anAn
[Note that f(A) is obtained from f(x) by substituting the matrix A for the variable x and substituting the scalar matrix a0l for the scalar a0.] - If f(A) is the zero matrix, then A is called a zero or root of f(x).
- Example:
Suppose
Then
Suppose f(x) = 2x2 - 3x + 5 and g(x) = x2 + 3x - 10. Then
Thus A is a zero of the polynomial g(x).
Types of Matrices
- Row Matrix: If a matrix has only one row and any number of columns, is called a Row matrix, or a row vector ; e.g. [2 7 3 9] is a row matrix.
- Column Matrix: A matrix having one column and any number of rows is a called a column matrix is a column vector, example:
 is a column matrix
is a column matrix - Null Matrix of Zero Matrix: Any matrix in which all the elements are zeros is called a Zero matrix or Null matrix, i.e.,
 . In general, a m x n matrix in which each element is zero, is called anull matrix of the type m x n and is denoted by Omxn.
. In general, a m x n matrix in which each element is zero, is called anull matrix of the type m x n and is denoted by Omxn. - Square Matrix: A matrix in which the number of rows is equal to the number of columns is called a square matrix i.e. A = (aij)mxn is a square matrix if and only if m=n.
 are square matrices.
are square matrices. - Diagonal Matrix: A square matrix is a called a diagonal matrix if all its non-diagonal elements are zero i.e. in general a matrix A = (aij)mxn is called a diagonal matrix if aij = 0 for i ≠ j;
for example is a diagonal matrix of order 3 x 3 i.e. 3 alone.
is a diagonal matrix of order 3 x 3 i.e. 3 alone. - Unit or Identity Matrix: A square matrix is called a unit matrix if all the diagonal elements are unity and non-diagonal elements are zero.
 are Identity matrices of order 3 x 3 and 2 x 2 respectively.
are Identity matrices of order 3 x 3 and 2 x 2 respectively. - Symmetric Matrix: A square matrix is called symmetric if for all values of i and j, aij = aji . ⇒ A’ = A i.e. transpose of the matrix A = A ;
 is a symmetric matrix of order 3x 3 .
is a symmetric matrix of order 3x 3 . - Skew Symmetric Matrix: A square matrix is called skew symmetric matrix if aij = -aji, for all values of i and j and all its diagonal elements are zero. ⇒ A’ = - A i.e. transpose of the matrix A = -A;
example. is a skew symmetric matrix of order 3 x 3.
is a skew symmetric matrix of order 3 x 3. - Triangular Matrix: A square matrix, in which all its elements below the leading diagonal are zero, is called an up per triangular matrix while square matrix, all of whose elements above the leading diagonal are zero, is called a lower triangular matrix.

- Transpose of Matrix: If in a given matrix, we interchange the rows and the corresponding columns, the new matrix obtained is called the transpose of the matrix A and is denoted by A or At or AT.


- Orthogonal Matrix: A square matrix A is called an orthogonal matrix if the product of the matrix A with its transpose matrix A’ is an identity matrix.
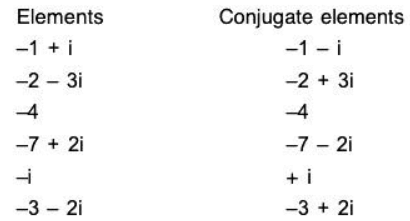
i.e. AA’ = I. - Conjugate of a Matrix:


∴ Conjugate of matrix

- Matrix Aθ : Transpose of the conjugate of a matrix A is denoted by Aθ

we have
and
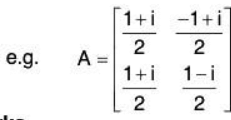
- Unitary Matrix: A square matrix A is said to be unitary, if we have AθA =1

Remarks- A real matrix is unitary if and only if it is orthogonal.
- If P is unitary so
 are also unitary.
are also unitary. - If P and Q are unitary so PQ is unitary multiple.
- If P is unitary, then I P I is of unit modulus.
- Any two Eigen vectors corresponding to the distinct Eigen values of a unitary matrix are orthogonal.
- If P is orthogonal so PT and P-1 are also orthogonal.
- If P and Q are orthogonal so PQ is also orthogonal.
- If P is orthogonal, then IPI = ± 1.
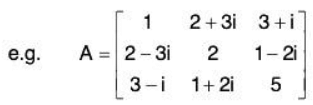
- Hermitian Matrix: A square matrix A = (aij) is said to be Hermitian Matrix if every i- jth element of A is equal to conjugate complex of j - ith element of A, or in order words


The necessary and sufficient condition for the matrix A to be Hermitian is that A = Aθ i.e. conjugate transpose of .
. - Skew Hermitian Matrix: A square A = (aij) is said to be a Skew Hermitian matrix if every j-ith element of A is equal to negative conjugate complex of j-ith element of A; i.e

All the elements of the principal diagonal are of the form: Hence aij is purely imaginary i.e. aij = 0 + ib or aij = 0.
Hence aij is purely imaginary i.e. aij = 0 + ib or aij = 0.
i.e. all the diagonal element of a Skew Hermitian Matrix are either zeros or pure imaginary.
Thus the necessary and sufficient condition for a matrix A to be Skew Hermitian is that
Properties- If A is a Skew-Hermitian matrix, then kA is also Skew-Hermitian for any real number k.
- If A and B are Skew-Hermitian matrices of same order, then λ1A +λ2B is also Skew Hermitian for real number λ1,λ2.
- If A and B are Hermitian matrices of same order, then AB-BA is Skew-Hermitian.
- If A is any square matrix, then A - A* is Skew-Hermitian matrices.
- Every square matrix can be uniquely represented as the sum of a Hermitian and a Skew Hermitian matrices.
- If A is a skew-Hermitian (Hermitian) matrix, then iA is a Hermitian matrix, then
 also Skew-Hermitian (Hermitian).
also Skew-Hermitian (Hermitian).
- Idempotent Matrix: A matrix such that A2 = A is called Idempotent Matrix.

- Periodic Matrix: A matrix A is said to be a Periodic Matrix if Ak+1 = A, where k is a +ve integer. If k is the least +ve integer for which Ak +1 = A then k is said to be period of A. If we choose k = 1, then A2 = A and we call it to be an idempotent matrix.
- Invoiutory Matrix: A matrix A is said to an involutory matrix if A2 = I (unit matrix). Since A2 = I always, we conclude that Unit matrix is always involutory.
- Nilpotent Matrix: A matrix is said to be a Nilpotent matrix if Ak = 0 (null matrix) where k is +ve integer; if however k is the least +ve integer of which Ak = 0, then k is called as the index of the nilpotent matrix.
The matrix is nilpotent and its index is 2.
is nilpotent and its index is 2. - Submatrix: A matrix obtained from a given matrix, say A = (aij)mxn by deleting some rows or columns or both is called a submatrix of A.
- Principal diagonal: The elements a11, a33, ..., amn of a square matrix of order mxm are called diagonal elements and the diagonal containing these elements is called the principal diagonal. In a square matrix (aij)m x m, aij is the diagonal element if i = j.
- Bi-diagonal Matrix:A matrix with elements only on the main diagonal and either the super-diagonal or sub-diagonal.
- Block Matrix: A matrix partitioned in sub-matrices called blocks.
- Block-diagonal Matrix: A block matrix with entries only on the diagonal.
- Boolean Matrix: A matrix whose entries are all either 0 or 1
- Permutation Matrix: A matrix representation of a permutation, a square matrix with exactly one I in each row and column, and all other elements 0.
- Vandermonde Matrix: a matrix with the terms of a geometric progression in each row, i.e., an m x n matrix

The determinant of a square Vandermonde matrix

Companion Matrix: The square matrix defined as

And the monic polynomial denotes the characteristics equation
p(t) = c₀ + c₁t + ⋯ + cₙ₋₁tⁿ⁻¹ + tⁿ
Rank of Matrix
Rank of Matrix
Minor of a Matrix
- Let A be a matrix square or rectangular, from it delete all rows leaving a certain t rows and all columns leaving a certain t columns.
Now if t > 1 then the elements that are left, constitute a square matrix of order t and the determinant of this matrix is called a minor of A of order t. - A single element of A may be consider as minor of order 1.
Rank of a Matrix
- A number r is said to be the rank of a matrix A if it possesses the following two properties.
1. There is at least one minor of A of order r which does not vanish.
2. Every minor of A of order (r + 1) or high vanish. Ail minors of order greater than r will vanish if all minors of order (r + 1) are zero. - Rank of a matrix is the order of the highest non-vanishing minor of the matrix. From the above definition we have the following two useful results.
1. The rank of matrix A is ≥ r, if there is at least one minor of A of order r which does not vanish.
2. The rank of matrix A is ≤ r if all the minors of A of order (r + 1) or higher vanish. - The rank of a matrix whose minors of order n are all zero is < n. We assign the rank n to the matrix which has at least one non-zero minor of order n; n being the order of any highest minor of the matrix, e.g. the rank of every onward non-singular matrix is n.
- Again rank of every non-zero matrix is ≥ 1, we assign the rank zero to every zero matrix.
We shall denote the rank of matrix A by the symbol ρ(A).
Example. Find the rank of the matrix
= 1(21 - 9) - 2 (9 - 5) + 0 (27 - 35)
= 12 - 8 = 4 ≠ 0.
ρ(A) = 3
1. Rank of a Matrix (by elementary transformations of a matrix)
Consider a matrix A = (aij)m x n then its rank can be easily calculated by applying elementary transformations given below:
- Interchange any two rows (i.e. Rij) or columns (Cij).
- Multiplication of the elements of a row (or a column) say Ri(or Ci) by a non zero number k is denoted by k Ri(or kCi)
- The addition to the elements of ith row (or column) the corresponding elements of any other row say jth row (or column) multiplied by a non zero number k is denoted by Rij(k) or Cij(k). Any elementary operation is called a row transformation (or a columntransformation) according as it operates on row (or column). In easy form we use the following notations:
- Ri ↔ Rj (interchange of ith and jth row) (Ci ↔ Cj (interchange of ith and jth column)
- Ri ↔ k Ri(Ci → k Ci) means multiply ith row (or column) by k ≠ 0.
- R.↔ Ri + kRj (Ci → Ci + kC) means multiply each element of jth row (or column) by non zero number k and add it to the corresponding elements of ith row (column).
The rank of a matrix does not alter by applying elementary row transformation (or column transformations).
2. Rank of a Matrix A = (aij)mxn by Reducing it to Normal Form.
Every non zero matrix [say A = (aij)mxn] of rank r, by a sequence of elementary row (or column) transformations be reduced to the forms: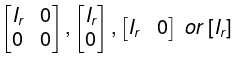 where lr is a rxr unit matrix o f order r and 0 denotes null matrix of any order. These forms are called as normal form or canonical form of the matrix A. The order or of the unit matrix lr is called the rank of the matrix A.
where lr is a rxr unit matrix o f order r and 0 denotes null matrix of any order. These forms are called as normal form or canonical form of the matrix A. The order or of the unit matrix lr is called the rank of the matrix A.
The rank of a matrix does not alter by pre-multiplication or post-multiplication with a non singular matrix.
3. Echelon Form of a Matrix
A matrix A = (aij)mxn is said to be in ECHELON FORM, if
- all the non-zero rows, if any, precede the zero rows,
- The number of zeros preceding the first nonzero element in a row is less than that the number of such zeros in the succeeding (or next) row,
- The first non-zero element in every row is unity.
- Example: the matrix
 is in echelon form.
is in echelon form.
Since in A,- The zero rows precede the zero row.
- The number of zero preceding the first non zero element in rows R2, R3, R4 are 1, 2 and 5 which are in ascending order.
- The first non zero element in each row is 1.
NOTE: When a matrix is converted in Echelon form, then the number of non zero rows of the matrix is the rank of the matrix A.
Example. Determine the rank of the matrix, by E-transformations.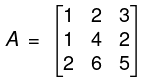
Now,
Now applying the elementary transformations.
R3→ R3 - R2, we have
or
Here third order minor viz(vanishes) while the second order minor
so the rank of the matrix is 2.
Inverse of a Matrix
- Definition: Let A be a square matrix. If there exists a matrix B, such that AB = I = BA, Where I is an unit matrix, then B is called the inverse of A and is denoted by A-1 and matrix A is called non-singular matrix. The matrix A is called non-singular matrix if such matrix B does not exist.
Note: The matrix B = A-1 will also be a square matrix of the same order as A.
- Following are the properties of Inverse of a matrix
1. Every invertible matrix possesses a unique inverse.
2. The inverse of the product of matrices of the same type is the product of the inverses of the matrices in reverse order i.e.
(AB)-1 = B-1 A-1, (ABC)-1 = C-1 B-1 A-1 and (A-1 B-1)-1 = BA.
3. The operations of a transpose and inverting are commutative, i.e. (A’)-1 = (A-1)’ where A is a m x n non-singular matrix, i.e. det A≠ 0.
4. If a sequence of elementary operations can reduce a non-singular matrix A of order n to an identity matrix, then the sequence of the same elementary operations will reduce the identity matrix ln to inverse of A.
i.e. If (Er.Er_1, E2 . E1)A = ln
then (Er.Er_1 .. E2.E1) ln = A-1.
This is also known as Gauss-Jorden reduction method for finding inverse of a matrix.
5. The inverse of the conjugate transpose of a matrix A (order m x n) is equal to the conjugate transpose of the matrix inverse to A, i.e. ( Aθ)-1 = (A-1)θ. - Method of finding inverse of a non-singular matrix by elementary transformations.
The method is that we take A and I (same order) and apply the row operations on both successively elementary transformations till A become I. When A reduces to I, I reduces to A-1. - Example. Find the inverse of the matrix

Write A = IA
By R2 - 2R1, R3 - 3R1
By R2 + R3
By R, + 3R3, R2 - 3R3
By R2 + 2R2
By - R2, - R3
⇒ I = BA
Inverse of a Matrix (another form)
- The inverse of A is given by

The necessary and sufficient condition for the existence of the inverse of a square matrix A is that IAI ≠ 0, i.e. matrix should be non-singular. - Properties of inverse matrix:
If A and B are invertible matrices of the same order, then
- ( A-1)-1 = A.
- (AT)-1 = (A-1)T
- (AB)-1 = B-1A-1
- (Ak)-1 = (A-1)k , k ∈ ℕ
- adj(A-1) = (adj A)-1

- A = diag (a1,a2....an) ⇒ A-1 = diag (a1-1a2-2..., an-1)
- A is symmetric matrix ⇒ A-1 is also symmetric matrix.
- A is a diagonal matrix, IAI ≠ 0 ⇒ A-1 is also a triangular matrix.
- A is a scalar matrix ⇒ A-1 is also a scalar matrix.
- A is a triangular matrix, IAI ≠ 0 ⇒ A-1 is also a triangular matrix.
- Every invertible matrix possesses a unique inverse.
- Cancellation law with respect to multiplication
If A is a non-singular matrix i.e., if IAI ≠ 0, then A-1 exists and
AB = AC ⇒ A-1 (AB) = A-1(AC)
⇒ (A-1A)B = (A-1A)C
⇒ IB = IC ⇒ B = C
∴ AB = AC ⇒ B = C = ⇔ IAI ≠ 0.
Determinants
Determinants
- Consider the following simultaneous equations
a11x + a12y = k1,
a21x + a22y = k2
these equations have the solution
provided the expansion a11a22 - a12a21 ≠ 0. - This expression a11a22 - a12a21 is represented by

and is called a determinant of second order. - The number a11,a12,a21,a22 are called elements of the determinant. The value of the determinant is equal to the product of the elements along the principal diagonal minus the product of the off-diagonal elements.
- Similarly a symbol
 is called a determinant of order 3 and
is called a determinant of order 3 and
its value is given by
= a11 (a22a33 - a32a23) - a12(a21a33 - a31a23 ) + a13(a21a32 - a31a22) ...(1
Properties of Determinants
- The value of the determinant does not change by changing rows into columns and columns into rows

- If any two adjacent rows (or columns) of a determinant are interchanged, the value of the determinant is multiplied by -1.

Note: In case any row (or column) of a determinant A be passed over n rows (or columns) then the resulting determinant is (-1)n Δ.
(fourth row has passed over three parallel rows) - If any two rows or two columns of a determinant are identical then the determinant are identical then the determinant vanishes.
- If all the elements of any row (or any column) of a determinant are multiplied by the same factor k then the value of new determinant is k times the value of the given determinant.
- If in a determinant each element in any row (or column) consists of the sum of r terms, the determinant can be expressed as the sum of r determinants of the same order.
- If to the elements of a row (or column) of a determinant are added m times the corresponding elements of another row (or column), the value of the determinant so obtained is equal to the value of the original determinant.
General rule. One should always try to bring in as many zeros as possible in any row (column) and then expand the determinant with respect to that row (column)
Thus
Minors and cofactors
Minors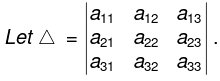
If we omit the row and the column passing through the element aij, then the second order determinant so obtained is called the minor of the element aij and is denote by Mij.
Therefore 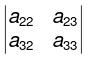 is minor of a11.
is minor of a11.
Similarly 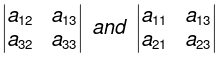 are the minors of the elements a21 and a32 respectively.
are the minors of the elements a21 and a32 respectively.
Cofactors:
The minor Mij multiplied by (-1)i+j is called the cofactor of the element aij. Cofactor of aij =Aij = (-1)i+j Aij.
Properties of Determinants
- When at least one row (or column) of a matrix is a linear combination of the other rows (or columns) the determinant is zero.
- The determinant of an upper triangular or lower triangular matrix is the product of the main diagonal entries.
- The determinant of the product of two square matrices is the product of the individual determinants:
|A.B| = IA|.|B|
One immediate application is to matrix powers:
IAI2 = IAI.IAI
and more generally IAnl = IAIn for integer n. - The determinant of the transpose of a matrix is the same as that of the original matrix:
IATI = IAI.
|
98 videos|28 docs|30 tests
|
FAQs on Matrices and Determinants- 1 - Mathematics for Competitive Exams
| 1. What is the rank of a matrix and how is it determined? |  |
| 2. How can I find the inverse of a matrix? |  |
| 3. What is a determinant and why is it important in linear algebra? |  |
| 4. What methods can be used to calculate the determinant of a matrix? |  |
| 5. Can you explain the relationship between the rank of a matrix and its determinant? |  |

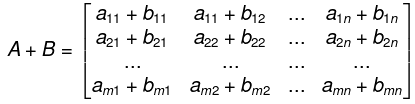
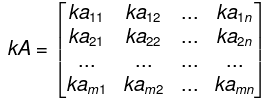
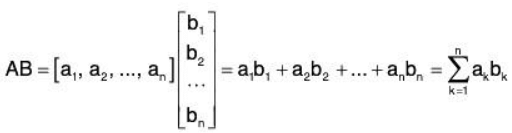 We emphasize that AB is a scalar (or a 1 x 1 matrix). The product AB is not defined when A and B have different numbers of elements.
We emphasize that AB is a scalar (or a 1 x 1 matrix). The product AB is not defined when A and B have different numbers of elements.
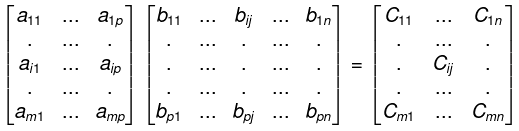 where
where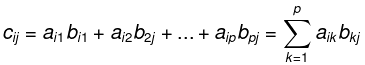
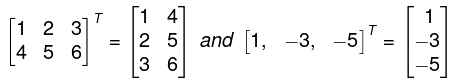 In other words, if A = [aij] is an m x n matrix, then AT = [bij] is the n x m matrix where bij = aji.
In other words, if A = [aij] is an m x n matrix, then AT = [bij] is the n x m matrix where bij = aji. 
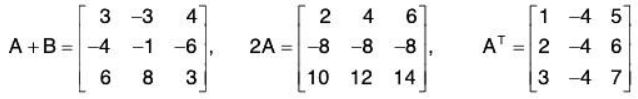
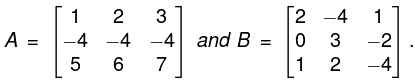
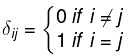
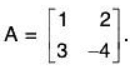 Then
Then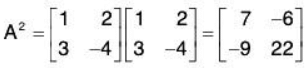
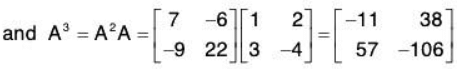
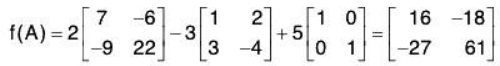
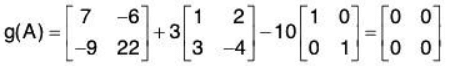
 is a column matrix
is a column matrix . In general, a m x n matrix in which each element is zero, is called anull matrix of the type m x n and is denoted by Omxn.
. In general, a m x n matrix in which each element is zero, is called anull matrix of the type m x n and is denoted by Omxn.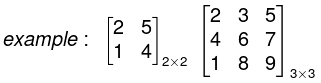 are square matrices.
are square matrices. is a diagonal matrix of order 3 x 3 i.e. 3 alone.
is a diagonal matrix of order 3 x 3 i.e. 3 alone.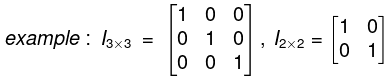 are Identity matrices of order 3 x 3 and 2 x 2 respectively.
are Identity matrices of order 3 x 3 and 2 x 2 respectively.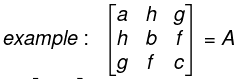 is a symmetric matrix of order 3x 3 .
is a symmetric matrix of order 3x 3 . is a skew symmetric matrix of order 3 x 3.
is a skew symmetric matrix of order 3 x 3.

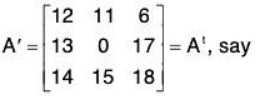
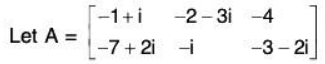
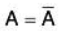
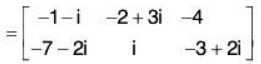
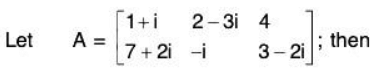
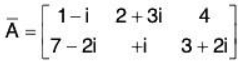
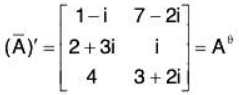
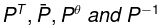 are also unitary.
are also unitary.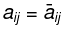
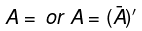 .
.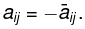
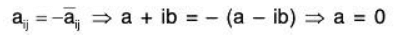 Hence aij is purely imaginary i.e. aij = 0 + ib or aij = 0.
Hence aij is purely imaginary i.e. aij = 0 + ib or aij = 0.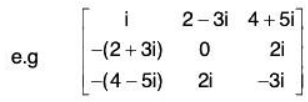
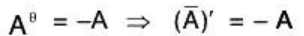
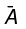 also Skew-Hermitian (Hermitian).
also Skew-Hermitian (Hermitian).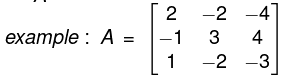
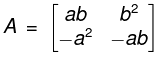 is nilpotent and its index is 2.
is nilpotent and its index is 2.
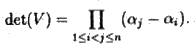

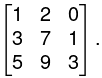
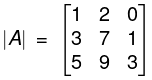
 is in echelon form.
is in echelon form.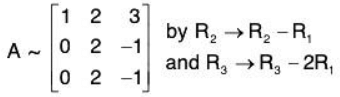
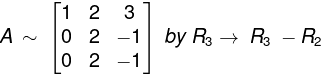
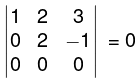 (vanishes) while the second order minor
(vanishes) while the second order minor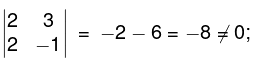 so the rank of the matrix is 2.
so the rank of the matrix is 2.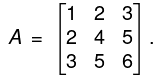

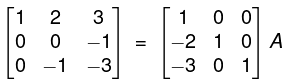
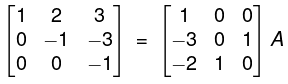
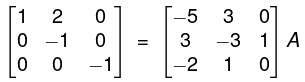
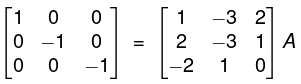
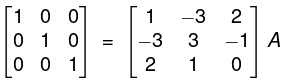
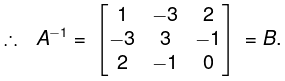

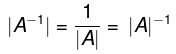
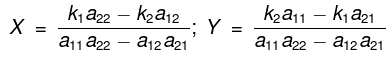

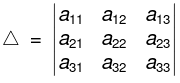 is called a determinant of order 3 and
is called a determinant of order 3 and