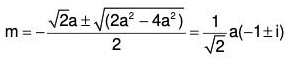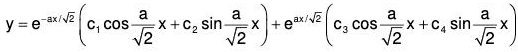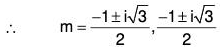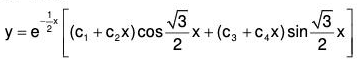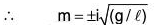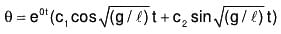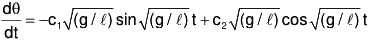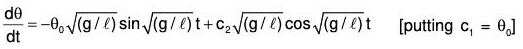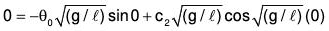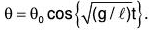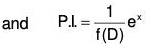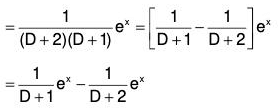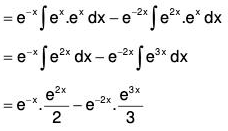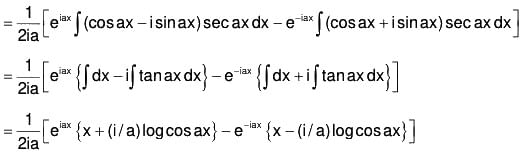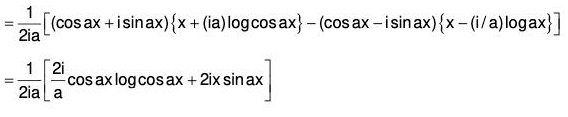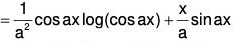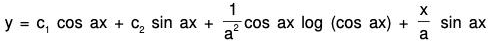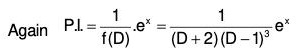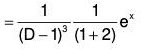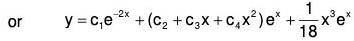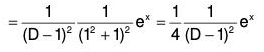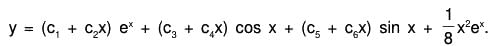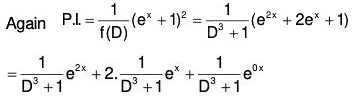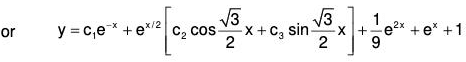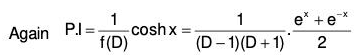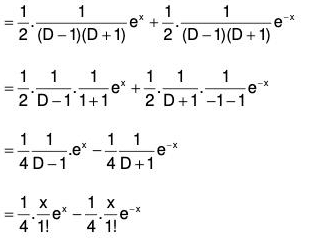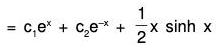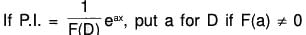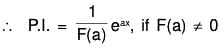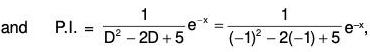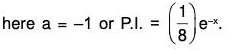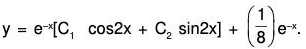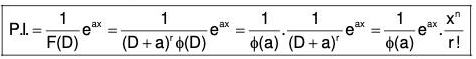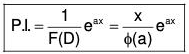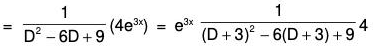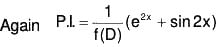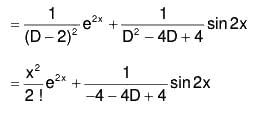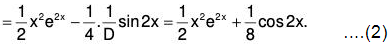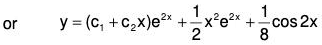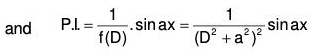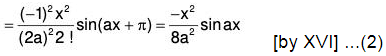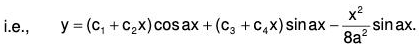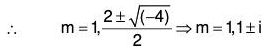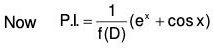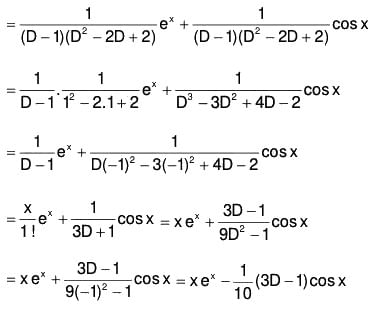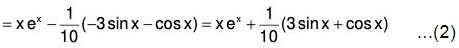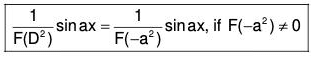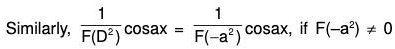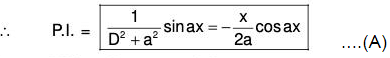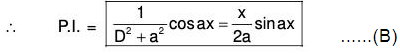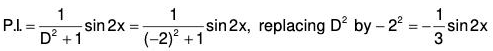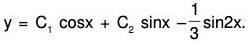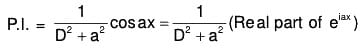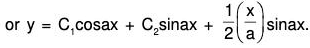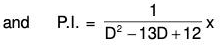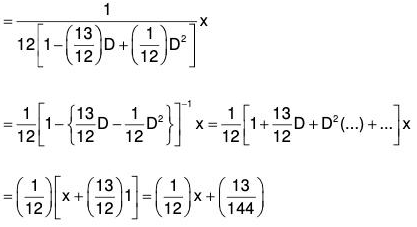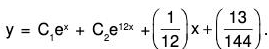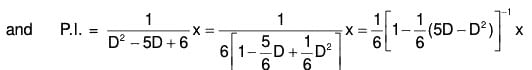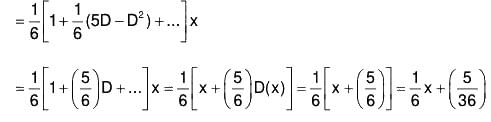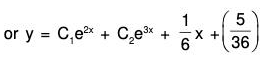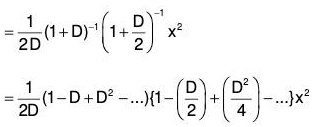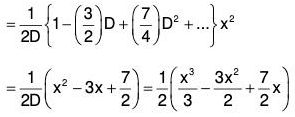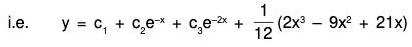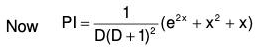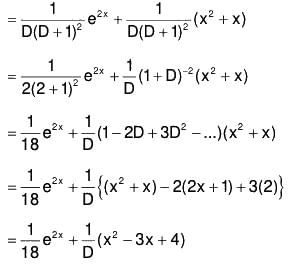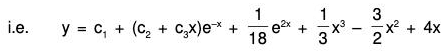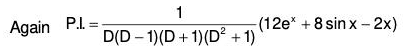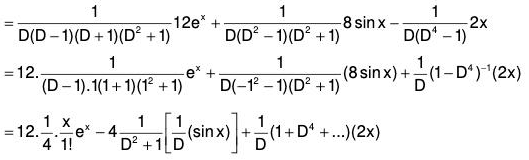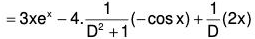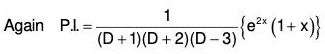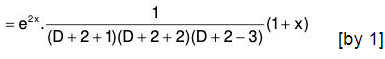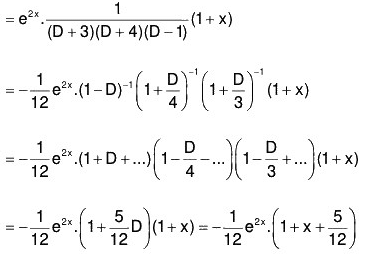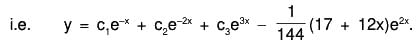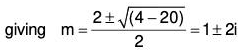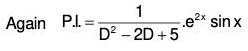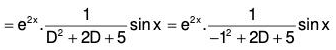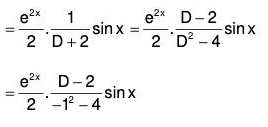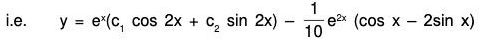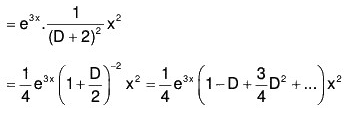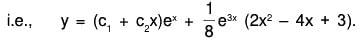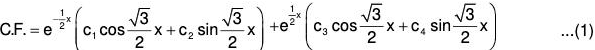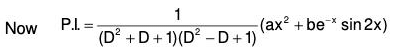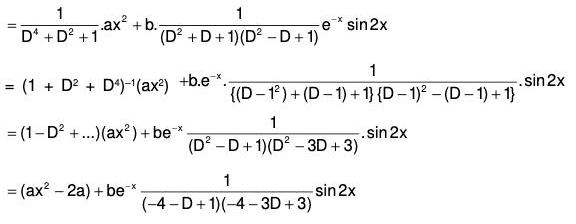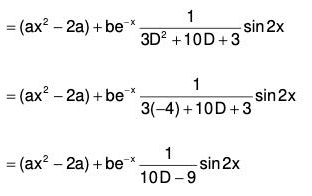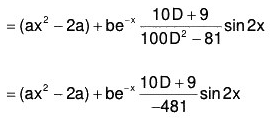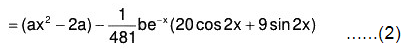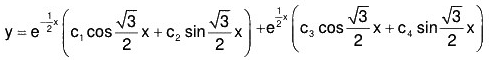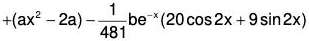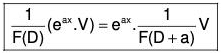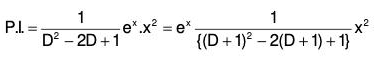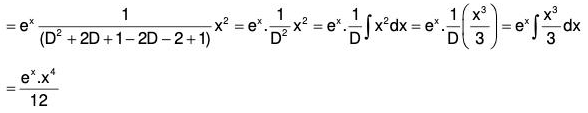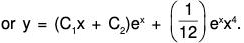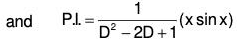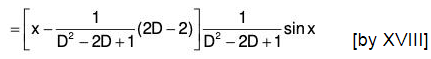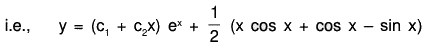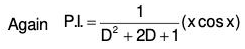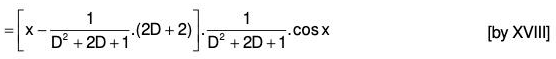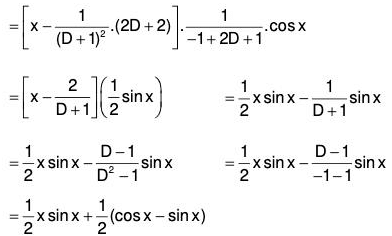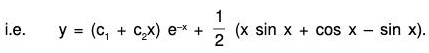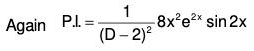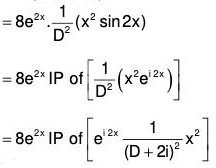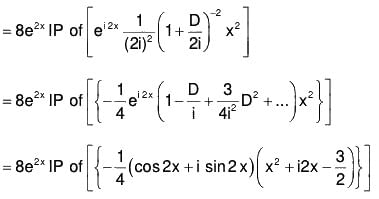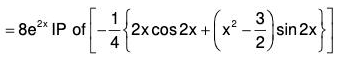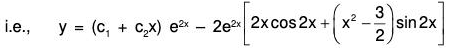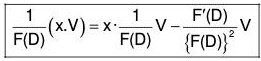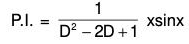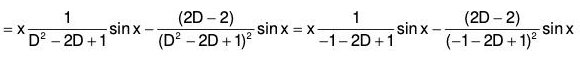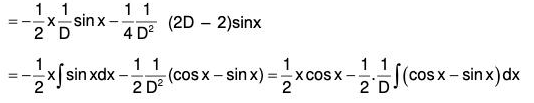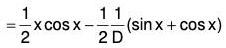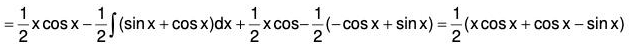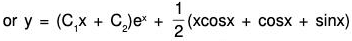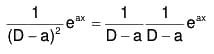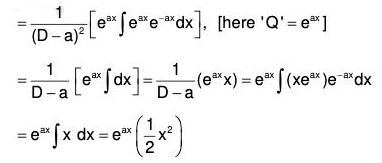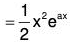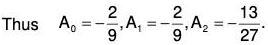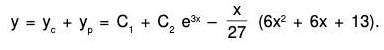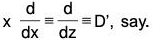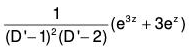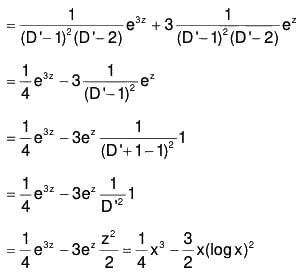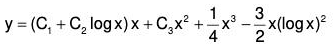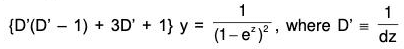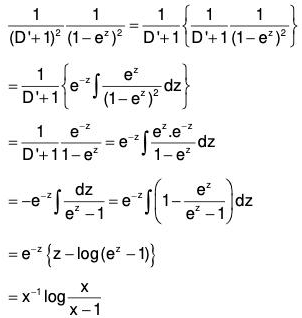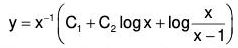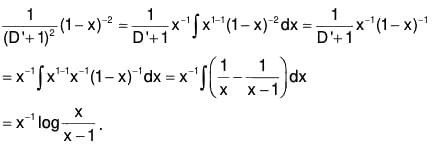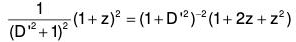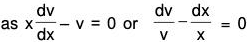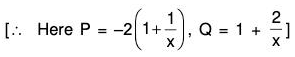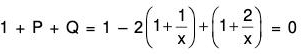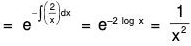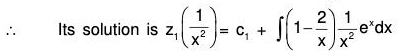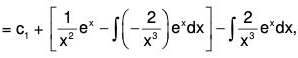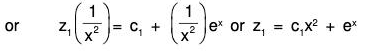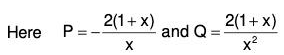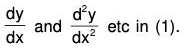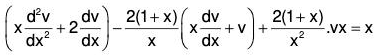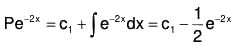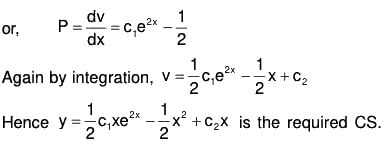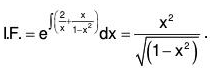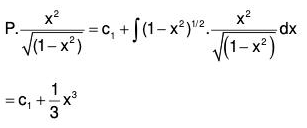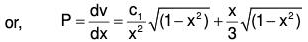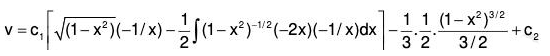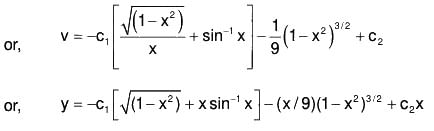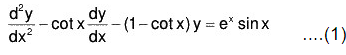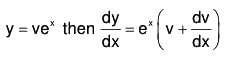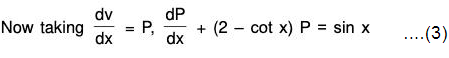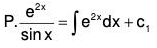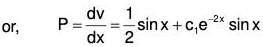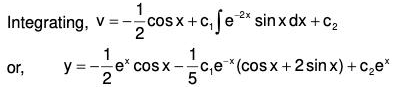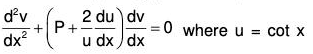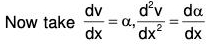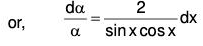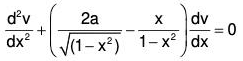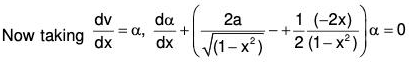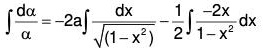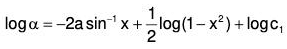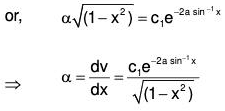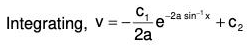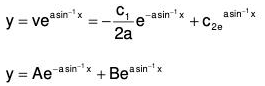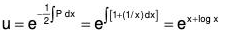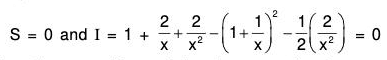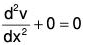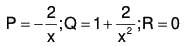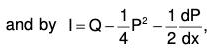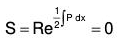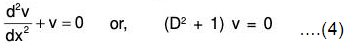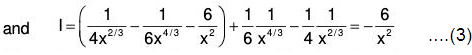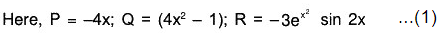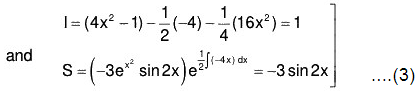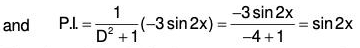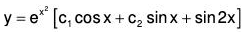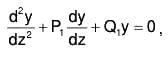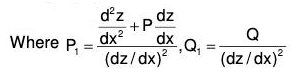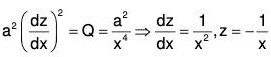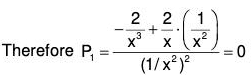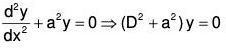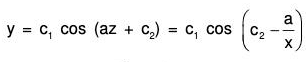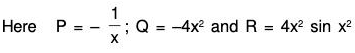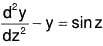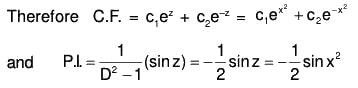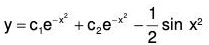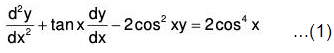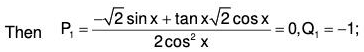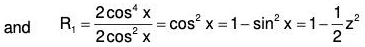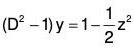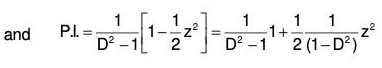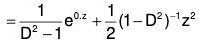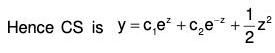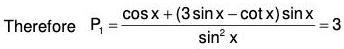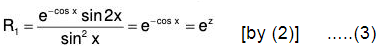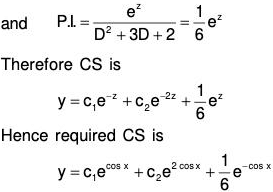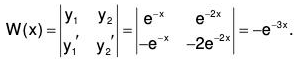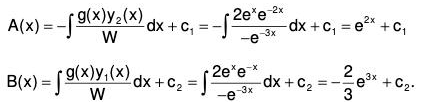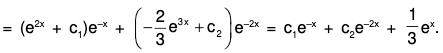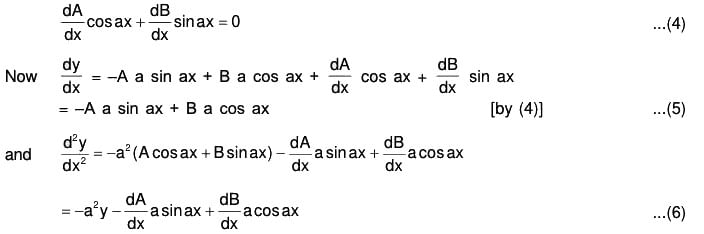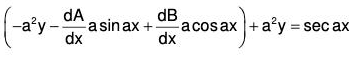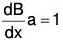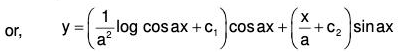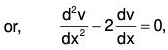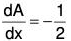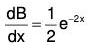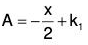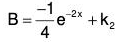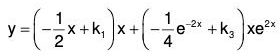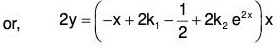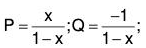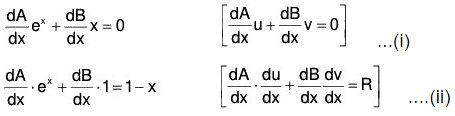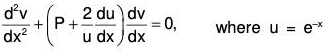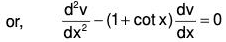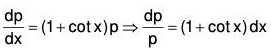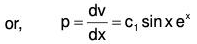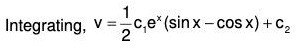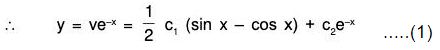Differential Equations- II | Mathematics for Competitive Exams PDF Download
Introduction
Definition
The general form of linear equation of order n is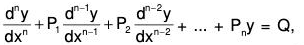 ...(1)
...(1)
where Q and P1, P2, P3, ...., Pn are all constants or functions of x.
If P1, P2, P3, ..... Pn are all constants (Q may not be constant), then the equation is said to be a linear differential equation with constant coefficients.
Differential Operator D
The derivatives of different orders of the dependent variable y w.r.t. the independent variable x are expressed as follows: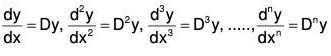
Clearly 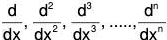 have been used for the symbols D, D2, D3, .........., Dn respectively which are differential operators of different orders. Using these operators, the differential equation (1) can be written as follows:
have been used for the symbols D, D2, D3, .........., Dn respectively which are differential operators of different orders. Using these operators, the differential equation (1) can be written as follows:
(Dn + P1Dn-1 + P2Dn-2 + .... + Pn)y = Q
or, in brief f(D)y = Q ...(2)
It can be easily seen that the above operators obey the fundamental law algebra:
(i) Law of indices : Dm.Dn = Dm+n
(ii) Commutativity : Dm + Dn = Dn + Dm
Dm.Dn = Dn.Dm = Dm+n
(D - α)(D - β) = (D - β)(D - α), where α, β are constants.
(iii) Distributivity : Dm (u + v) = Dm (u) + Dm (v).
D can be operated like an algebraic symbol.
For example,
(D2 + 2D + 1) sin x = D2 (sin x) + 2D (sin x) + sin x
= D[D (sin x)] + 2D (sin x) + sin x
= D(cos x) + 2cos x + sin x
= - sin x + 2cos x + sin x = 2 cos x
Inverse Operator [D-1]
We know the differentiation and Integration are the inverse operations. Therefore if D is used for the Derivative, then the symbol D-1 or 1/D is used for the inverse operation i.e. integration.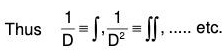
For example,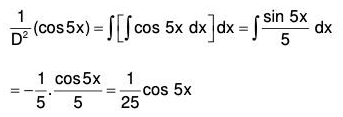
Linearly Independent (LI) and Linearly Dependent (LD)
The collection of functions y1, y2........y, is called LI if the only solution of the equation c1y1 + c2y2 + .... cn.yn = 0 is c1 = c2 = .... = cn = 0 where c1’s are constant otherwise it is called LD.
Hence by definition, it is clear that
Two functions are LD iff one function is a constant multiple of the other.
For example : If y1 = x and y2 = 3x then y1 and y2 are LD, because then non zero solutions of c1x + c2(3x) = 0 are c1 = - 3 and c2 = 1.
Wronskian Collection Definition
The Wronskian defines the determinant of the collection of n functions W (y1, y2, .... , yn) as follows: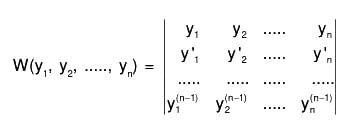
where dash (‘) denotes the derivative.
Wronskian Test for LI
(i) The functions y1, y2, .... yn are LI if and only if W(y1, y2, ...., yn) ≠ 0
(ii) The functions y1, y2, ..... yn are LD if and only if W (y1 , y2, ....... yn) = 0
Example : The function ex and x ex are LI because x ex is not a constant multiple of ex.
Homogeneous and Non Homogeneous Linear Differential Equations
When Q = 0, f(D)y = 0 is called homogeneous otherwise Non Homogeneous.
Properties:
1. If y = f(x) is any solution of the equation f(D)y = 0, then y = cf(x) is also a solution of the equation, where c is any arbitrary constant.
2. If y = f1(x) and y = f2(x) are the two solutions of f(D)y = 0, then y = c1 f1(x) + c2 f2(x) will also a solution of the equation where c1 and c2 are arbitrary constants.
Complementary Function and Particular Integral
The general form of the equation is
f(D)y = 0 ...(1)
If Q = 0, then it will be of the form
f(D)y = 0 .....(2)
If the solution of the equation (2) is taken as y = y1, then on substituting the value of y, we will see that y = c1y1 will also be a solution where c1 is an arbitrary constant.
Similarly if n LI function
y = y1, y = y2, ........y = yn
are also the solutions of the equation (1), then
f(D)y1 = 0 = f(D)y2 = f(D)y3 = .... = f(D)yn ......(3)
Now if c1, c2, c3.......cn are arbitrary constant, then c1y1 + c2y2 + c3y3 + .... + cnyn will also be a general solution of the equation (2), because
f(D)(c1y1 + c2y2 + .... + cn yn)
= cnfn(D)y1 + c2f(D)y2 + .... cnf(D)yn
= c1(0) + c2(0) + .... + cn(0) = 0 [by (3)]
or f(D)u = 0
where u = c1y1 + c2y2 + .... cnyn .....(4)
Clearly u is a general solution of the equation (2) because the number of arbitrary constants is equal to its (u) order.
Again if PS of equation (2) is v, then
f(D)v = Q .......(5)
then f(D)(u + v) = f(D)u + f(D)v
= 0 + Q [from (4) and (5)]
= Q
Therefore the general form of CS of equation (1) is y = (c1y1 + c2y2 + ..... + cnyn) + v
or y = u + v
In this solution u and v are called the Complementary Function (CF) and Particular Integral (PI) of the solution respectively.
Therefore the GS of any equation is of the following form :
y = CF + PI .....(6)
Remarks :
1. If in equation (1), Q = 0, then its CS (complete solution) will be y = CF.
2. In CF, the number of arbitrary constants is equal to the order of equation.
3. In PI, there is no arbitrary constant.
Methods for Finding CF
In order to find the CF of the given DE, first of all assume the function Q on the RHS of the equation to zero, i.e., write the equation in the following form
or, in the symbolic form,
(Dn + P1 Dn-1 + .... + Pn) y = 0
or f(D) y = 0 ....(1)
Let y = emx be the solution of (1), then substituting the value of Dy, D2y, ....., Dny
emx [mn + P1 mn-1 + P2mn-2 + .... + Pn] = 0
or mn + P1 mn-1 + P2mn-2 + .... + Pn = 0 [∵ emx ≠ 0]
From this it is clear that y = emx will be a solution of (1), if m is a solution of the equation mn + P1mn-1 + P2mn-2 + .... + Pn = 0
or f(m) = 0 .....(2)
The above equation (2) is known as the Auxiliary Equation or in brief AE of the equation (1).
Case I : When all the roots of AE are different :
Suppose m1, m2, .... , mn are the roots of AE f(m) = 0 and are all different.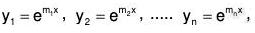 are the n distinct LI solutions and
are the n distinct LI solutions and
The GS will be:
y = c1y1 + c2y2 + .... + cnyn = C.F.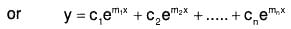 ....(1)
....(1)
Case II : When roots of AE are same (repeated) :
Suppose AE f(m) = 0 has two equal roots (m1 = m2) and rest of different roots are :
m1 = m2 > m3, m4........ mn
In this case the solution will be :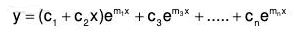 ...(2)
...(2)
If three roots of AE are equal say m1 = m2 = m3, then in this case the solution will be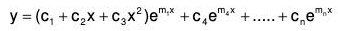 ...(3)
...(3)
Similarly solution can be written in case of more equal roots.
Case III : When the roots of AE are complex :
Suppose a pair of roots of AE are complex say α ± β, then the solution of the corresponding equation is :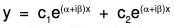
which can be written in the convenient form as :
y = eαx (c1 cos βx + c2 sin βx) ....(4)
The above form can be converted in the following compact form :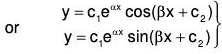 ....(5)
....(5)
Hence the CS of the equation will be :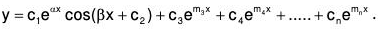
Case IV : When roots of AE are complex and equal (repeated) :
Let the AE has a pair of complex roots α ± β repeated once, then the solution of the corresponding equation will be :
y = (c1 + c2x)e(α+iβ) + (c2 + c4x)e(α+iβ)x
which can be written in the simplest form as follows :
y = eax[(c1 + c2x)cos βx + (c3 + c4x)sin βx] ...(6)
and CS will be :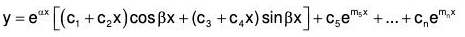
When roots of AE are real and in the surd form :
Such roots always occur in pairs. Let the roots be in the surd form a±√b, then the solution of the corresponding equation will be :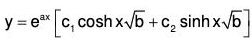 ......(7)
......(7)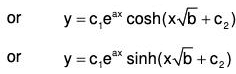
Example 1: 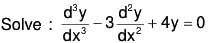
The given equation can be written as (D3 - 3D2 + 4) y = 0
The AE of the given equation is m3 - 3m2 + 4 = 0or (m + 1) (m2 - 4m + 4) = 0
or (m + 1) (m - 2)2 = 0 ⇒ m = 2, 2, -1
Therefore the GS is y = (c1 + c2x)e2x + c3e-x
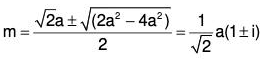
Example 2: Solve : (D4 + a4) y = 0
The AE of the given equation is m4 + a4 = 0
or m4 + 2m2a2 + a4 - 2m2a2 = 0
or (m2 + a2)2 - (√2 ma)2 = 0
or (m2 + a2 + √2 ma) (m2 + a2 - √2 ma) = 0
when m2 + √2 ma + a2 = 0 then
and when m2 - √2 ma + a2 = 0, then
Therefore GS is
Example 3: Solve : (D4 + 2D3 + 3D2 + 2D + 1)y = 0
The AE of the given equation is m4 + 2m3 + 3m2 + 2m + 1 = 0
or (m2 + m + 1)2 = 0
Therefore GS is
Example 4:
when for t = 0, θ = θ0 and dθ/dt = 0.
The given equation can be written as (ℓD2 + g)θ = 0
The AE of the given equation is ℓm2 + g = 0
Therefore GS is
∵ For t = 0, θ = θ0∴ From (1), θ0 = c1 cos + c2 sinθ ⇒ c1 = θ0. ....(2)
Again differentiating (1),
or
Now since at t = 0, dθ / dt is also zero, therefore
⇒ c2 = 0 ....(3)
Substituting the values of c1 and c2 in (1), the required solution is
Symbolic operator
(D2 - D) (x2 - x) = 3 - 2x, we have 
General Method of Finding PI
First of all, we shall find the value of 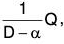 where α is any constant.
where α is any constant.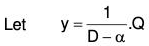
∴ (D - α)y = Q
or Dy - αy = Q
or 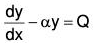
which is a linear equation in the variable y. Multiplying both sides by the Integrating Factor IF = e-αx and then integrating, we have
ye-ax = ∫Q.e-αx dx + c
or y = eαx ∫Q.e-αx dx + ceαx
Since we want a particular solution of this equation, therefore if c can be taken to be zero, then y = eαx∫e-αx.Qdx
or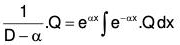 ....(9)
....(9)
Now we can find the value of 1/f(D).Q with the help of (9)
The value of the integral is obtained by resolving f(D) into linear factors and 1/f(D) into fractions and integrating, we obtain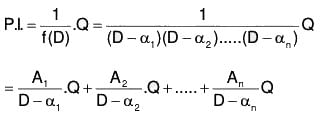
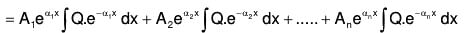
Example 1: Solve (D2 + 3D + 2)y = ex
The AE of the given equation is m2 + 3m + 2 = 0
or (m + 2)(m + 1) = 0
⇒ m = - 2, - 1
Therefore
C.F. = c1e-2x + c2e-x ......(1)...(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
y = c1e-2x + c2e-x + (1/6)ex
Example 2: Solve : (D2 + a2) y = sec ax
The AE of the given equation is m2 + a2 = 0
∴ m = ± ia
Therefore C.F. = e0x [c1 cos ax + c2 sin ax]
= c1 cos ax + c2 sin ax ....(1)
Therefore the GS is y = C.F. + P.l.
i.e.
Shorter Method for Finding PI in Some Special Cases
If Q in the different equation f(D)y = Q is of the following special form, then their PI can be found by the short methods discussed below :
1. eax, where a is any constant.
2. sinh ax, cosh ax.
3. xn, where n is a positive integer.
4. eax V, where V is any function of x.
5. xV, where V is any function of x.
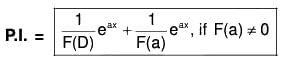
(1) PI for eax, where a is any constant and F(a) ≠ 0
PI for eax :
Here we have to find the value of 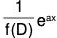 when f(a) ≠ 0.
when f(a) ≠ 0.
From successive differentiation we know that
Dn(eax) = an eax
Now f(D) (eax) = [Dn + P1Dn-2 + P2Dn-2 + ...+ Pn] (eax)
= Dn (eax) + P1Dn-1 (eax) +...+ Pn(eax)
= an eax + P1an-1eax + ...+ Pneax
= (an + P1an-1 + P2dn-2 + ...+ Pn)eax
∴ f(D)(eax) = f(a)eax .......(1)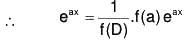
 [by (1)]
[by (1)]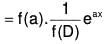
Now if f(a) ≠ 0, then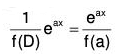 ......(X)
......(X)
Special case:
(i) When f(a) = 0, then
i.e., when a is a non-repeated root of f(D) = 0
∴ (D - a) is a factor of f(D)
Let f(D) = (D - a) ϕ(D) where ϕ(a) ≠ 0.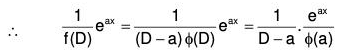 [∵ ϕ(a) ≠ 0]
[∵ ϕ(a) ≠ 0]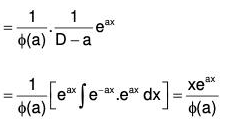
(ii) If a is a root repeated r times,
i.e., (D - a)r is a factor of f(D), then let
f(D) = (D - a)r Ψ(a) where Ψ(a) ≠ 0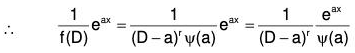 [∵ Ψ(a) ≠ 0]
[∵ Ψ(a) ≠ 0]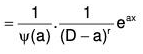
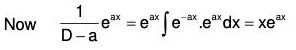
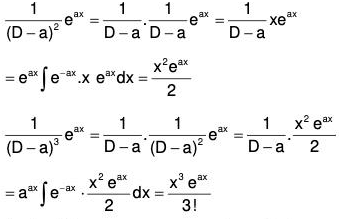
Continuing in this manner, we may show that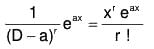
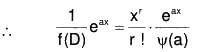 .....(XI)
.....(XI)
(iii) If Q = sinh(ax) or cosh(ax), then
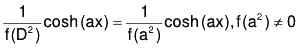 .....(XII)
.....(XII)
Example 1: Solve : {(D + 2)(D - 1)3} y = ex
The AE of the given equation is (m + 2) (m - 1)3 = 0
⇒ m = -2, 1, 1, 1
Therefore C.F. = c1e-2x + (c2 + C3x + c4x2) ex ....(1)....(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 2: Solve : {(D - 1)2(D2 + 1)2} y = ex
The AE of the given equation is (m - 1)2 (m2 + 1)2 = 0
∴ m = 1, 1, ± i ± i
Therefore C.F. = (c1 + c2x) ex + e0x [(c3 + c4x) cos x + (c5 + c6x) sin x]
= (c1 + c2x) ex + (c3 + c4x) cos x + (c5 + c6x) sin x ....(1)....(2)
Therefore the GS is
Example 3: Solve : (D3 + 1) y = (ex + 1)2
The AE of the given equation is m3 + 1 = 0
or (m + 1) (m2 - m + 1) = 0
∴ m = -1, 1/2 (1 ± √3i)
Therefore, the GS is y = C.F. + P.l. = (1) + (2)
Example 4: Solve : (D2 - 1)y = cosh x
The AE of the given equation is m2 - 1 = 0
or (m - 1)(m + 1) = 0 ⇒ m = 1, -1
Therefore C.F. = c1ex + c2e-x ....(1)....(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)Working Rule
Example 5: Solve (D2 - 2D + 5)y = e-x.
Flere auxiliary equation is m2 - 2m + 5 = 0, whose roots are m = -1 ± 2i
∴ C.F. = e-x[C1 cos2x + C2 sin2x], where C1 and C2 are arbitrary constants.
∴ The required solution is y = C.F. + P.l. i.e.
Special case: If a is a root repeated r times
When a is non-repeated:
Example 6: Solve (D2 - 6D + 9)y = 4x3x.
Here the auxiliary equation is m2 - 6m + 9 = 0 or m = 3, 3.
∴ C.F. = (C1x + C2)e3x, where C1, C2 are arbitrary constants and P.l.
∴ The required solution is y = C.F. + P.l. or y = (C1x + C2)e3x + 2x2e3x.
(2) P.l. for sinax or cosax and F(-a2) ≠ 0
We have to find 1/f(D2) sin ax and 1/f(D2) cos ax when f(-a2) ≠ 0.
We know that D(sin ax) = a cos ax
D2(sin ax) = -a2 sin ax
D3(sin ax) = -a3 cos ax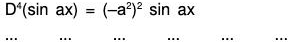
In general, (D2)n sin ax = (-a2)n sin ax
∴ f(D2) sin ax = f(-a2) sin ax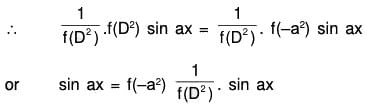
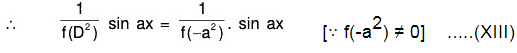
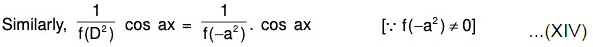
Special Case : If (D2 + a2)n is one of the factor, then the above method fails
∵ f(-a2) = 0 and in such a case we proceed as follows :
We know that eiax = cos ax + i sin ax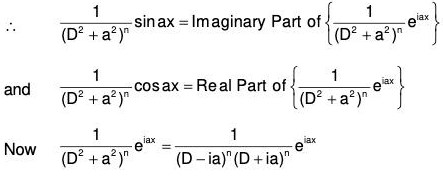
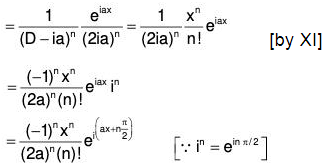
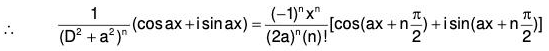
Equating real and imaginary parts, we have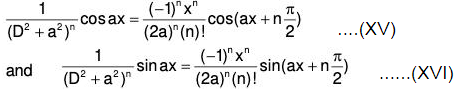
Remark :
1. If f(D) contains odd powers of D also, it can be put in the form
f(D) = f1(D2) + Df2(D2).
2. When f (-a2) = 0, it is convenient to use the procedure given above instead of using the formula directly.
Example 1: Solve : (D2 - 4D + 4)y = e2x + sin 2x
The AE of the given equation is m2 - 4m + 4 = 0
or (m - 2)2 = 0 ⇒ m = 2, 2
Therefore C.F. = (c1 + c2x)e2x ....(1)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 2: Solve : (D2 + a2)2 y = sin ax
The AE of the given equation is (m2 + a2)2 = 0
∴ m = ± ai, ± ai
Therefore C.F. = e0x [(c1 + c2x) cos ax + (c3 + c4x) sin ax]
= (c1 + c2x)cos ax + (c3 + c4x) sin ax. ....(1)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 3: Solve : (D3 - 3D2 + 4D - 2) y = ex + cos x
The AE of the given equation is m3 - 3m2 + 4m - 2 = 0
or (m - 1) (m2 - 2m + 2) = 0
Therefore C.F. = c1ex + ex(c2 cos x + c3 sin x) ....(1)
Therefore, the GS is y = C.F. + P.l. = (1) + (2)
when F(-a2) = 0
(I) Let F(D) = D2 + a2 and Q = sinax.
(II) Let F(D) = D2 + a2 and Q = cosax.
Example 4: Solve (D2 + 1)y = sin2x.
Here the auxiliary equation is m2 + 1 = 0 or m = ± i.
∴ C.F. = C1 cosx + C2 sinx, where C1 and C2 are arbitrary constants and
∴ The requires solution is
Example 5: Solve (D2 + a2)y = cosax.
Here the auxiliary equation is m2 + a2 = 0 or m = ± ai
∴ C.F. = C1cos ax + C2sin ax, where C’ s are arbitrary const, and
∴ The requires solution is y = C.F. + P.l.
(3) PI for xm 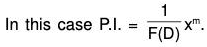
Working Rule
Take out the lowest degree term from F(D) and the remaining factor will be of the form [1 + f(D)] or [1 - f(D)] and this factor can be taken in the numerator with a negative index which can be expanded with the help of Binomial Theorem. The expansion is to be carried upto the term Dm, since Dm+1xm = 0, Dm+2xm = 0 and all other higher differential coefficients of xm are zero.
Example 1: Solve (D2 - 13D + 12)y = x.
Here auxiliary equation is m2 - 13m + 12 = 0 or (m - 12)(m - 1) = 0 or m = 1, 12
∴ C.F. = C1ex + C2e12x, where C’s are arbitrary constants
∴ Required solution is y = C.F. = P.l.
Example 2: Solve (D2 - 5D + 6)y = x.
Its C.F. = C1e2x + C2e3x, where C1 and C2 are arbitrary constants.
∴ The complete solution is y = C.F. + P.l.
Example 3: Solve : (D3 + 3D2 + 2D) y = x2
The AE of the given equation is m3 + 3m2 + 2m = 0
or m(m + 1)(m + 2) = 0 ⇒ m = 0, - 1, - 2
Therefore C.F. = c1e0x + c2e-x + c3e-2x
= c1 + c2e-x + c3e-2x .....(1).....(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 4: Solve : (D3 + 2D2 + D)y = e2x + x2 + x
The AE of the given equation is m3 + 2m2 + m = 0
or m(m2 + 2m + 1) = 0
or m (m + 1)2 = 0 m = 0, - 1 , - 1
Therefore CF = c1e0x + (c2 + c3x)e-x
= c1 + (c2 + c3x)e-x .....(1)....(2)
the GS is y = CF + PI = (1) + (2)
Example 5: Solve : (D5 - D) y = 12ex + 8 sin x - 2x
The AE of the given equation is m5 - m = 0
or, m(m - 1)(m + 1)(m2 + 1) = 0
∴ m = 0, 1, -1 , ± i
C.F. = c1e0x + c2ex + c3e-x + (c4 cos x + c5 sin x)
Therefore = c1 + c2ex + c3e-x + c4 cos x + c5 sin x ....(1)[by IV]
= 3xex + 2xsinx + x2 .....(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
i.e. y = c1 + c2ex + c3e-x + c4 cos x + c5 sin x + 3xex + 2x sin x + x2.
(4) PI for eax.V, where V is a function x
Here we have to find the value of 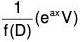
Consider any function V1 of x to be determined later on in terms of the given function V. By successive differentiation, we have
D(eax V1) = eax DV1 + aeax V1 = eax (D + a) V1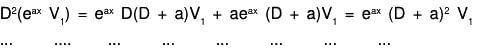
Dn(eax V1) = eax (D + a)n V1
∴ f(D) (eax V1) = eax f(D + a) V1 ....... (1)
Put f(D + a) = V1 so that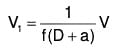 ....(2)
....(2)
Eliminating V1 from (1) and (2), we obtain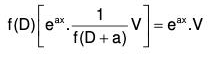
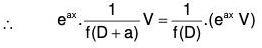
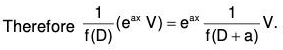 ....(XVII)
....(XVII)
Now the value of 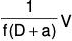 can be determined by the methods discussed earlier.
can be determined by the methods discussed earlier.
Remark : This method can also be used to find the value of 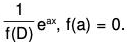 In this case V = 1.
In this case V = 1.
Example 1: Solve : (D3 - 7D - 6) y = e2x (1 + x)
The AE of the given equation is m3 - 7m - 6 = 0
or (m + 1) (m2 - m - 6) = 0
or (m + 1) (m - 3) (m + 2) = 0
∴ m = -1, -2, 3
Therefore C.F. = c1e-x + c2e-2x + c3e3x ......(1)......(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 2: Solve : (D2 - 2D + 5) y = e2x sin x.
The AE of the given equation is m2 - 2m + 5 = 0
Therefore C.F. = ex(c1 cos 2x + c2 sin 2x) ...(1)[by XVII]
....(2)
Therefore, the GS is y = C.F. + P.l. = (1) + (2)
Example 3: Solve : (D2 - 2D + 1) y = x2e3x
The AE of the given equation is m2 - 2m + 1 = 0
or (m - 1)2 = 0 m = 1, 1
Therefore C.F. = (c1 + c2x)ex ....(1)....(b)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 4: Solve : (D4 + D2 + 1) y = ax2 + be-x sin 2x
The AE of the given equation is m4 + m2 + 1 = 0
or (m2 + 1)2 - m2 = 0
or (m2 + m + 1) (m2 - m + 1) = 0
Therefore
Therefore the GS is y = C.F. + P.l. = (1) + (2)
When Q is of the form eax.V, where V is any function of x then
Example 5: Solve (D2 - 2D + 1)y = ex.x2.
Here the auxiliary equation is m2 - 2m + 1 = 0 or m = 1, 1.
∴ C.F. = (C1x + C2)ex, where C1 and C2 are arbitrary constants and
∴ The required solution is y = C.F. + P.l.
or (m - 1) 2 = 0 ⇒ m = 1 , 1
Therefore C.F. = (c1 + c2x)ex ....(1).....(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 6: Solve : (D2 + 2D + 1) y = x cos x
The AE of the given equation is m2 + 2m + 1 = 0
or (m + 1)2 = 0 ⇒ m = -1, -1
Therefore C.F. = (c1 + c2x)e-x .....(1)....(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
Example 7: Solve : (D2 - 4D + 4) y = 8 x2 e2x sin 2x.
The AE of the given equation is m2 - 4m + 4 = 0
or (m - 2)2 = 0 ⇒ m = 2, 2
Therefore C.F. = (c1 + c2x)ex ....(1)[by formula XVII]
...(2)
Therefore the GS is y = C.F. + P.l. = (1) + (2)
when Q is of the form xV, where V is any function of x
Example 8: Solve (D2 - 2D + 1)
Flere the auxiliary equation is m2 - 2m + 1 = 0 or (m - 1)2 = 0 or m = 1, 1.
∴ C.F. = (C1x + C2)ex, where C1 and C2 are arbitrary constants and
∴ The required solution is y = C.F. + P.I.
To show thatdx, where Q is a function of x
Proof :Then (D - a) y = Q, operating with
which is linear equation in y whose integrating factor is e-ax. Its solution is ye-ax = ∫Qe-ax dx, (neglecting the constant of integration as P.l. is required)
or y = eax ∫Qa-ax dx Hence proved.
Example 9: 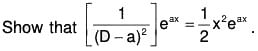
Hence proved.
Formation of linear differential equations, whose solutions are specified.
While solving linear differential equations with constant coefficients, we observed that if the auxiliary equation f(m) = 0 had a root m = α, then the operator f(D) had a factor (D - α) and a term such as Aeax occurred in the general solution of the equation. In the same way, we observed that Bxeax appeared in the solution only when f(D) contained a factor (D - α)2, Cx2eax only when f(D) contained (D - α)3 and so on. A, B, C , ..... are independent of x. We also observed that terms as Aeax sin βx or Beax cos βx, which occurred in the solution, correspond to roots m = α ± iβ of the auxiliary equation or to factor {(D - α)2 + β2} in the operator f(D).
With these facts in our possession, we try to form homogeneous linear differential equations, whose solutions are specified, assuming the superposition principle. For that, let the given function be (Ae2x + Bx), with no restrictions on A and B.
For the term Ae2x, we know that there will be a root m = 2 of the auxiliary equation and a factor (D - 2) of the operator f(D). The term Bx will appear, if the auxiliary equation has a double root m = 0, 0 and a factor D2 in f(D). Hence we see that the homogeneous linear equation.
D2 (D - 2) y = 0 ...(1)
that is, (D3 - 2D2) y = 0
has y = Ae2x + Bx + C as its general solution and hence y = Ae2x + Bx will be a particular solution of (1), of which A and B are constants.
Again, if the specified function be
y = 10 + 5xex + sin x, ...(2)
then we see that the term 10 is associated with the root m = 0 of the auxiliary equation, the term 5xex is associated with the double root m = 1, 1 of the auxiliary equation and the term sin x is associated with the pair of imaginary roots m = 0 ± i. Hence the auxiliary equation is m (m - 1)2 (m2 + 1) = 0
or, m5 - 2m4 + 2m3 - 2m2 + m = 0
The differential equation corresponding to this auxiliary equation is
(D5 - 2D4 + 2D3 - 2D2 + D) y = 0, ...(3)
the general solution of which is y = A + (B + Cx) ex + E sin x + F cos x.
With appropriate choice of the constants A = 10, B = 0, C = 5, E = 1, F = 0, the given relation (2) becomes a particular solution of the differential equation (3).
If again the specified function be
y = 7xex cos 3x ....(4)
and if we are to find the homogeneous linear differential equation with real constant coefficients of which this function is a particular solution, then we observe that the desired equation will have its auxiliary equation f(m) = 0, whose roots will be m = 1 ± 3i and 1 ± 3i. Hence the auxiliary equation will be
{(m - 1)2 + 9}2 = 0
or, m4 - 4m3 + 24m2 - 40m + 100 = 0.
Thus the desired equation will be
(D4 - 4D3 + 24D2 - 40D + 100) y = 0, ......(5)
the general solution of (5) will be y = ex (A + Bx) cos 3x + ex (E + Fx) sin 3x.
With appropriate choice of the constants A = E = F = 0 and B = 7, the given relation (4) becomes a particular solution of the differential equation (5).
Method of undetermined coefficients.
Let us consider the linear differential equation of n-th order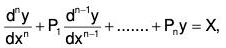 .....(1)
.....(1)
where P1, P2......... Pn are constants and X is a function of x only.
In symbolic notation, this can be written as f(D) y = X, where f(D) = Dn + P1Dn-1 + ..... + Pn.
We know that the general solution of the equation (1) may be expressed as y = yc + yP, where yc is the complementary function, that is, the general solution of the corresponding homogeneous equation f(D)y = 0 and yp is the particular integral, that is, any solution of the equation (1) containing no arbitrary constants.
The method of undetermined coefficients is one of the procedures for determining yp, when X is an exponential, a polynomial, a sine or cosine, or some combination of such functions only.
(i) Particular integral for X = eax, a being a constant.
The equation here is f(D)y = eax. ......(2)
Since the derivatives of eax are constant multiples of eax, it is reasonable to guess that the particular integral might also be a constant multiple of eax and we assume that
yp = Aeax .......(3)
might be a particular solution of the equation (2).
Here A is a constant (called the undetermined coefficient) to be determined, such that (3) actually satisfies (2).
Thus we get A f(a) eax = eax, giving A = 1/f(a) , provided f(a) ≠ 0.
If f(a) = 0, that is if a be a root of the auxiliary equation f(m) = 0, then (3) reduces the left hand side of (2) to zero. But the right hand side of (2) being different from zero, (3) possibly cannot satisfy (2), as it stands. In this case, we take
yp = A x eax as a trial solution.
If a be a double root of the auxiliary equation, then we take yp = Ax2 eax as a trial solution. In general, if a be a multiple root of the auxiliary equation of multiplicity r(<n), then we take yp = axr eax as a trial solution.
(ii) Particular integral for X = a0xk + a1xk-1 + ...... + ak, where k is a positive integer and a0, a1, ......aK are constants.
Here the equation is
f(D) y = a0xk + a1xk-1 + ...... + ak. .....(4)
Since the derivative of a polynomial is also a polynomial, we assume that
yp = A0xk + A1xk-1 + ...... + Ak .....(5)
might be a particular solution of the equation (4), if Pn ≠ 0.
Here A0, A1, ..... , Ak are constants (undetermined coefficients) to be determined, such that (5) satisfies (4). Substituting (5) in (4) and equating like powers of x from both sides, we get the values of A0, A1, ....., Ak.
If Pn = 0 (that is, if there be no term containing y), then putting (5) in (4), we see that the highest power of x on the left hand side of (4) is xk-1 but that on the right hand side of (4) is xk. So, in this case, we take yp = x(A0xk + A1xk-1 + ..... + Ak).
If Pn = 0 and Pn-1 = 0 , then we take yp = x2 (A0xk + A1xk-1 + ..... + Ak).
In general, if the last r P’s be zero but Pn-r ≠ 0, then we take
yp = xr (A0xk + A1xk-1 + ..... + Ak).
(iii) Particular integral for X = sin ax or cos ax.
Let the equation be f(D)y = sin ax. .....(6)
Since the derivatives of sin ax are constant multiples of sin ax and cos ax, we take
yp = A sin ax + B cos ax ......(7)
as a trial solution of the equation (6), provided (7) does not satisfy the homogeneous equation f(D) y = 0. Here A and B are constants (undetermined coefficients) and are obtained by putting (7) in (6) and equating the resulting coefficients of sin ax and cos ax from both sides.
If (7) satisfies the equation f(D)y = 0, (that is if (7) be a part of yc), then we take yp = x(A sin ax + B cos ax) as a trial solution.
Note. If X be a linear combination of eax, sin bx and ∑anxk-n then the particular integral is obtained by following the superposition principle.
If X be of the form eax sin bx or eax(∑anxk-n) or (∑anxk-n) sin bx or eax (∑anxk-n) sin bx, then yp is modified accordingly. For example, if X = eax sin bx, where a is not a root of the auxiliary equation and sin bx is not a part of yc. then we take yp = (A1eax) (B1 sin bx + C1 cos bx), that is yp = eax (A sin bx + B cos bx).
Example 1: Obtain linear differential equation with real constant coefficients, that is satisfied by the following functions :
(i) y = x2 - 8 sin 4x; (ii) y = 4e-x cos 3x + 12e-x sin 3x.
(i) The term x2 will appear, if the auxiliary equation has a multiple root of multiplicity 3 and m = 0, 0, 0. The term sin 4x will be given by a pair of imaginary roots 0 ± 4i. The corresponding auxiliary equation is m3 (m2 + 16) = 0, that is, m5 + 16m3 = 0.
Hence the given function is a solution of the homogeneous linear differential equation
(D5 + 16D3) y = 0 ...(1)
Note. The general solution of the equation (1) is y = A + Bx + Cx2 + E sin 4x + F cos 4x.
The choice of the constants A = B = F = 0, C = 1 and E = - 8 justifies that the given function is a particular solution of the equation (1).
(ii) The roots of the auxiliary equation corresponding to the terms of the given function are (-1 ± 3i).
The auxiliary equation is thus (m + 1)2 + 9 = 0 or m2 + 2m + 10 = 0.
The corresponding linear homogeneous differential equation with constant coefficients is (D2 + 2D + 10) y = 0
Example 2: Solve, by the method of undetermined coefficients the equation (D2 + 1) y = 10e2x, with the conditions y = 0 and Dy = 0 when x = 0.
Here the auxiliary equation is m2 + 1 = 0 , which gives m = ± i.
Hence the complementary function (yc) is (C. cos x + C2 sin x), where C1 and C2 are arbitrary constants.
In this case, 2 is not a root of the auxiliary equation. So we assume that the particular integral is yp = Ae2x, where A is a constant to be determined, such that yp satisfies the given equation.
This gives (D2 + 1) yp = 10e2x
or (D2 + 1) Ae2x = 10e2x
or (4 + 1) Ae2x = 10e2x, giving A = 2.
Thus the general solution is given by
y = yc + yp = C1 cos x + C2 sin x + 2e2x.
Therefore, Dy = - C1 sin x + C2 cos x + 4e2x.
To find C1 and C2, we use the given initial conditions.
From the condition y = 0 when x = 0, we get C1 = -2 and from the condition Dy = 0 when x = 0, we get C2 = -4.
Hence the required solution of the equation is y = 2e2x - 2cos x - 4sin x.
Example 3: Solve, by the method of undetermined coefficients, the equation (D2 - 3D) y = 2x2 + 1.
The auxiliary equation is m2 - 3m = 0, giving m = 0, 3.
Therefore yc is (C1 + C2e3x), where C1 and C2 are arbitrary constants.
In this case, there is no term containing y. So we assume yp = x(A0x2 + A1x + A2) where A0, A1, A2 are constants to be determined, such that yp satisfies the given equation. In other words,
(D2 - 3D)yp = 2x2 + 1
or, (D2 - 3D) (A0x3 + A1x2 + A2x) = 2x2 + 1
or, 6 A0x + 2 A1 - 3(3 A0x2 + 2 A1x + A2) = 2x2 + 1
or, -9 A0x2 + (6 A0 - 6 A1)x + (2A2 - 3 A2) = 2x2 + 1.
Equating like powers of x from both sides, we get
-9 A0 = 2, 6 A0 - 6 A1 = 0, 2 A1 - 3A2 = 1.
Hence the general solution is
Cauchy-Euler Equation
Cauchy’s Linear Equation
A differential equation of the form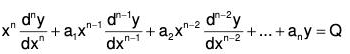
where a1, a2,..,an are constants and Q is either a constant or a function of x alone is called a Non-Homogeneous Linear Differential Equation.
When Q = 0 then we say it is nth order Homogeneous Linear Differential Equation
Note : The degree of x and the order of derivative is same in each term.
First method of solving non-homogeneous DE:
The homogeneous linear differential equation is transformed into a linear equation with constant coefficients by changing the independent variable x to z by the substitution.
z = log x or x = ez ...(1)
Differentiating wrt x,
dz/dx = 1/x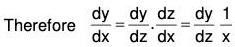
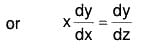 .....(2)
.....(2)
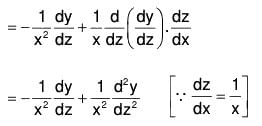
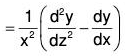 .....(3)
.....(3)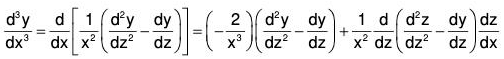
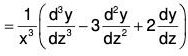 .....(4)
.....(4)
Similarly  can also be determined.
can also be determined.
Now if we take d/dz = D, then by (2), (3), (4) ...., we observe that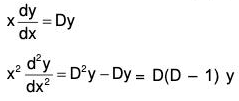
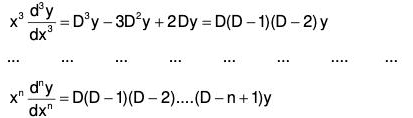
Therefore, the given equation becomes
[{D(D - 1 ) (D - 2)...(D - n + 1)} + a1{D(D - 1) (D - 2)...(D - n + 2)} + ... + an] y = Z ...(5) where Z is a function of z into which Q is changed.
Clearly equation (1) is a linear differential equation with constant coefficients, which can be solved by the earlier methods.
The Auxiliary Equation AE of the above transformed equation (5) is {m(m - 1) (m - 2)....(m - n + 1)} + a1{m(m - 1) (m - 2) ....(m - n + 2)} + ... + an = 0 which is a nth degree equation in m giving n values of m.
Let m = m1, m2,....mn be the roots of this equation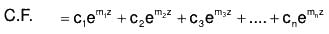
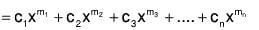 ...(6)
...(6)
Particular Cases :
(i) When two roots of AE are equal, Let m1 = m2, then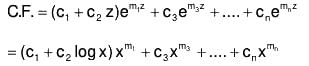
(ii) When three roots of AE are equal, Let m1 = m2 = m3, then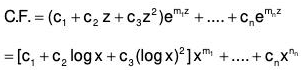
(iii) When two roots of AE are complex, say α ± i β, then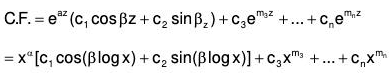
(iv) When the complex roots a ± i β are repeated twice, then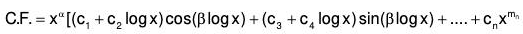
Now the solution of the equations can be obtained by finding the Particular Integrals [PI] by the methods already discussed earlier and then GS = CF + PI
Another method of solving non-homogeneous linear equation:
In this method, the independent variable is not changed into another variable but solved directly. We know that if z = log x, then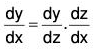

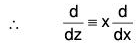
If we denote the operator x(d/dx) = θ, then equation (6) of First method of solving nonhomogeneous DE can be expressed as :
[{θ(θ - 1) (θ - 2)...(θ - n + 1)} + a1{θ(θ - 1)...(θ - 2)...(θ - n + 2)} +...+ an] y = Q ...(1)
or f(θ) y = Q ...(2)
(a) C.F. : It is obtained by solving the equation f(θ) y = 0.
Let y = xm be a solution of (2), then by (1)
[{m(m - 1) (m - 2)....(m - n + 1)} + a1 {m(m - 1) (m - 2)... (m - n + 2)} +....+ an] xm = 0
or [m(m - 1) (m - 2)....(m - n + 1)} + a1 {m(m - 1) (m - 2)... (m - n + 2)} +....+ an] = 0
[∵ xm ≠ 0]
or f(m) = 0 ...(3)
which is a nth degree equation in m let m1, m2, ...,mn be the n roots of equation (3), the GS of (2) i.e, CF is given by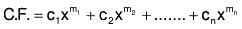
Note. AE (3) is obtained by simply writing θ = m in equation (2).
(b) PI : Let y = u be a PS of equation (1), then f(θ) u = Q
If 1/f(θ) be the inverse operator of f(0), then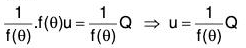
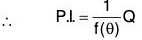
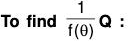
First we find the value of 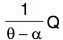
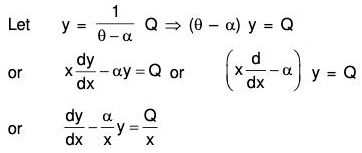
which is a linear equation where I.F. = e∫-α/x dx = e-α logx = x-α. Multiplying both sides by th e Integrating Factor and then integrating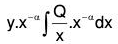

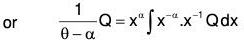 ....(1)
....(1)
Now we can evaluate 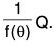
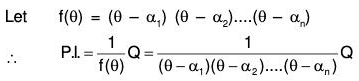
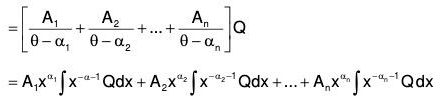
To find 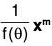 when f(m) ≠ 0.
when f(m) ≠ 0. 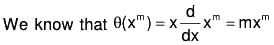
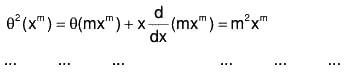
θn(xm) = mnxm
∴ f(θ) xm = f(m) xm 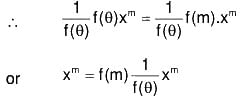
If f(m) ≠ 0, then ....(1)
....(1)
Particular Cases : When f(m) = 0, then
(θ - m) is a factor of f(θ)
Therefore let f(θ) = (θ - m) f(θ) where f(m) ≠ 0.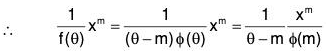
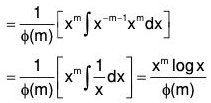
Similarly if m is a root repeated r times, so that (θ - m)r is a factor of f(θ) i.e.t
f(θ) = (θ - m)r ψ(θ) where ψ (m) ≠ θ.
In this case we can see that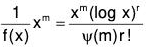 ....(2)
....(2)
Example 1: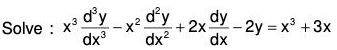
We first change the independent variable x to z by substitution x = ez, that is, z = logx, so that
The equation is then reduced to
D’(D' - 1) (D’ - 2) - D’(D’ - 1) + 2D’ - 2) y = e3z + 3ez
or, (D’3 - 4D’2 + 5D’ - 2) y = e3z + 3ez
or, (D’ - 1)2 (D' - 2) y = e3z + 3ez.
Here the auxiliary equation (m - 1)2 (m - 2) = 0 has the roots 1, 1, 2.
Thus the complementary function is (C1 + C2z) ez + C3 e2z = (C1 + C2 log x) x + C3x2.
The particular integral is
Hence the complete solution is
Example 2: Solve : (x2 D2 + 3xD + 1) y = 1/(1-x)2 , where D ≡ d/dx.
Let us put x = ez, so that z = log x.
The given equation then reduces to
Now, the roots of the auxiliary equation are - 1, - 1.
Thus the complementary function is
(C1 + C2z) e-z = (C1 + C2 log x) x-1.
The particular integral is
Hence the complete solution is
Note. The particular integral may also be obtained in the following way :
Example 3: Solve : (x4 D4 + 6 x3 D3 + 9x2D2 + 3xD + 1) y = (1 + log x)2, where D ≡ d/dx
Let us put x = ez, so that z = log x.
The given equation then reduces to {D’ (D’ - 1) (D’ - 2) (D’ - 3) + 6D’(D’ - 1) (D’ - 2) + 9D’ (D’ - 1) + 3D’ + 1} y = (1 + z)2.
Simplifying, we get (D’2 + 1)2 y = (1 + z)2.
Now, the roots of the auxiliary equation are ± i, ± i.
Thus, the complementary function is (C1 + C2z) cos z + (C3 + C4z) sin z
= (C1 + C2 log x) cos (log x) + (C3 + C4 log x) sin (log x).
The particular integral is
= (1 - 2D’2 + ....) (1 + 2z + z2)
= 1 + 2z + z2 - 4 = z2 + 2z - 3 = (log x)2 + 2 log x - 3.
Hence the complete solution is y = (C1 + C2 log x) cos (log x) + (C3 + C4 log x) sin (log x) + (log x)2 + 2 log x - 3.
Linear Equations of Second Order With Variable Coefficients
Definition
The Standard Form the linear equation of second order is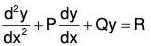 ....(1)
....(1)
or y2 + Py1 + Qy = R ....(2)
where P, Q, R are functions of x.
Method of Solution
Factorization of The Operator
Let the given equation be y2 + Py1 + Qy = R or (D2 + PD + Q)y = R, where D ≡ d/dx.
It will be possible in certain cases to factorise the left hand side into two linear operators in D acting on y. In such cases we first reduce the given equation to one of first order and then solve the given equation.
Example 1: Solve xy2 + (x - 1)y1 - y = 0.
Given equation may be written as
[xD2 + (x - 1)D - 1]y = 0, where D ≡ d/dx .....(1)
Now xD2 + (x - 1)D - 1 = xD2 + xD - D - 1
= xD(D + 1) - (D + 1) = (xD - 1)(D + 1) ...(2)
Note: But if we take (D + 1)(xD - 1), then
(D + 1)(xD - 1) = D(xD - 1) + (xD - 1) = D(xD) - D + xD - 1
= [xD2 + D(x).D] - D + xD - 1 = [xD2 + (1)D] - D + xD - 1 = xD2 + xD - 1, which is different from the left hand side of the problem.
∴ With the help of (2), the given equation (1) reduces to
(xD - 1)(D + 1)y = 0 .....(3)
Let (D + 1) y = v, .....(4)
Hence from (3) and (4),
we get (xD - 1)v = 0, .....(5)
which is a differential equation of first order in v.
Now (5) can be rewritten
Integrating, log v - log x = log c1, where c1 is arbitrary const, or log (v/x) = logc1
or v = c1x
or (D + 1)y = c1x, from (4) orwhich is a linear equation of first order in y. Its integrating factor = e∫dx = ex.
∴ The solution of (6) is y.ex = c2 + ∫c1xexdx = c2 + c1 ∫xexdx = c2 + c1[xex - ∫1.exdx], integrating by parts of yex = c2 + c1[xex - ex] or y = c2e-x + c1(x - 1) is the required solution.
Where c1, c2 are arbitrary constants.
One Integral Belonging to The Complementary Function
Let the given equation be
y2 + Py1 + Qy = R ...(i)
where P, Q and R are functions of x.
Let y = z be one known integral of the complementary function of (i) i.e. one integral of
y2 + Py1 + Qy = 0 ...(ii)
i.e. y = z is a solution of (ii) and
so z2 + Pz1 + Qz = 0 ...(iii)
Now let the complete solution of (i) be
y = vz, .......(iv)
where v is a function of x to be determined.
From (iv), we have
y1 = v1z + vz1 and y2 = (v2z + v1z1) + (v1z1 + vz2) = v2z + 2v1z1 + vz2.
Substituting these values of y, y1 and y2 in (i),
we get (v2z + 2v1z1 + vz2) + P(v1z + vz1) + Q(vz) = R
or v2z + v1(2z1 + Pz) + v(z2 + Pz1 + Qz) = R
or zv2 + (2z1 + Pz)v1 + v(0) = R,
from (iii)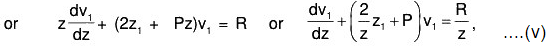
which is a linear equation of first order in v1.
From here we can obtain v1 i.e. dv/dx in the usual way which on integration gives the value of the unknown function v and then substituting this value of v in (iv), where z is already known, we get the complete solution of (i).
Rulse for finding the Complementary function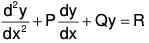
- If 1 + P + Q = 0, then complim entary function y = ex
- If 1 - P + Q = 0, then com plim entary function y = e-x
- If m2 + mP + Q = 0, then com plim entary function y = emx
- If P + Qx = 0, then complimentary function y = x
- If 2 + 2Px + Qx2 + 0, then comp lim entary function y = x2
- If m(m-1) + Pmx + Qx2 = 0, then complimentary function y = xm
Working method for finding solution of linear equation of second order :
- Put the given equation in the standard form
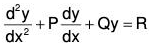 in which the coefficient of d2y/dx2 is unity.
in which the coefficient of d2y/dx2 is unity. - Find an integral of CF studied earlier.
If a solution u is given in a problem, then there is no need of this step. - Now take y = uv and simplify to the form of equation (4).
- Take dv/dx = P and reduce to a linear equation in p and x.
- Now find CS of the so obtained equation.
Example 1: Solve xy2 - 2(x + 1)y1 + (x + 2)y = (x - 2)e2x.
Reducing the given equation to the standard form
y2 + Py1 + Qy = R,
we have....(i)
And so we find that
∴ From Rule 1; y = ex is an integral belonging to the complementary function (i.e. C.F.) of (i)
∴ Let y = zex ...(ii)
be the complete integral (solution) of (i), where z is a function of x to be determined.
From (ii), we have y1 = + z1ex = (z1 + z)ex
and y2 = (z2 + z1)ex + (z1 + z)ex = (z2 + 2z1 + z)ex
Substituting these values of y, y1 and y2 in the given equation, we have
x(z2 + 2z1) + z)ex - 2(x + 1)(z1 + z)ex + (x + 2)zex = (x - 2)e2x
or xz2 + z1[2x - 2(x + 1)] + z[x - 2(x + 1) + (x + 2)] = (x - 2)exwhich is a linear equation of first order in z1.
Its integrating factor
integrating first integral by parts taking ex as 2nd function
or dz = (c1x2 + ex)dx,
Substituting this value of z in (ii), the required solution iswhere a = c1/3 , b = c2 are the arbitrary constants.
Example 2:
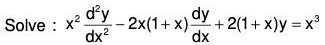
Dividing the given equation by x2 and putting in the standard form
.....(1)
Thus P + Qx = 0, Therefore y = x is a part of CF
Now taking y = vx and substituting....(2)
Putting dv/dx = P in (2), we have.....(3)
(3) is a linear equation whose I.F. = e-2x
Therefore solution of (3) is
Example 3:
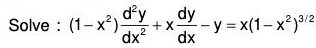
Here P + Qx = 0, Therefore y = x is a part of CF.
Now substituting y = vx, dy/dx and d2y/dx2 etc and simplifying,....(1)
Substituting dv/dx = P in (1),.....(2)
(2) is a linear equation whose
Therefore solution of (2) is
Again integrating,...(1)
Integrating the first factor by parts and substituting x2 = t in the second factor on RHS of (1), we obtain
which is the required CS.
Example 4: 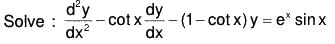
Clearly, P + Q + 1 = 0 , therefore y1 = ex is a solution.
Now,
Substituting these in the given equation,....(2)
(3) is a linear equation whose I.F. = e2x/sin x
Therefore solution of (3) is
which is the required CS.
Example 5: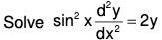
given y = cot x is a solution.
The given equation is
Clearly P = 0. Now putting y = v cot x,
Integrating log α = 4 ∫ cosec 2x dx + log c1
= 2 log tan x + log c1
or α = dv/dx = c1 tan2x
dv = c1(sec2 x - 1) dx
Integrating v = c1 (tan x - x) dx + c2
or y = c1 cot (tan x - x) + c, cot x which is the required CS.
Example 6: 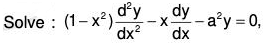
Given that 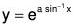 is a solution.
is a solution.
From the given solution, let CS of the given equation be
Find dy/dx and d2y/ dx2. Substituting in the equation and simplifying to
Separating the variables and integrating
Therefore the required CS is
Removal of the first derivative (Normal form):
To express the standard form of second order linear equation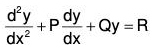 ....(1)
....(1)
in the normal form 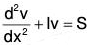
Let CS of (1) be y = uv where u and v are functions of x.
Differentiating this twice wrt x,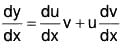
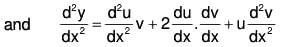
Substituting these in (2),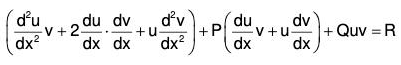
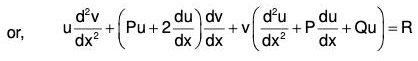
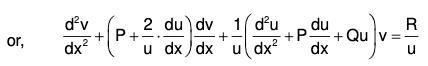 ....(2)
....(2)
Now to remove the first derivative dv/dx, equate its coefficient to zero
Integrating,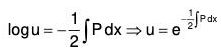 ....(3)
....(3)
Using (3) in (2), 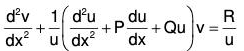 .....(4)
.....(4)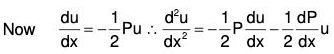
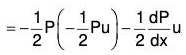
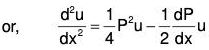
Using these in (4),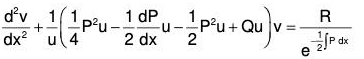
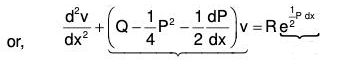
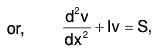 [Normal Form] ...(5)
[Normal Form] ...(5)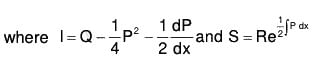 [Formula] .....(6)
[Formula] .....(6)
Working method:
- Write the given equation in the standard form (1) keeping the coefficient of d2y/dx2 as unity (1).
- Choose u = e1/2∫P dx to remove the first derivative.
- Now take y = uv as CS, reduce the given equation to the normal form d2v/dx2 + Iv = S, where
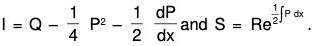
- Now (a) If I = constant, then use the earlier methods.
(b) If I = (constant / x2), then the resulting equation reduces to homogeneous form which can be solved by the earlier methods. - By the above method, get v so that CS is y = uv.
Example 1: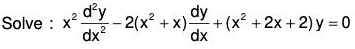
In order to put the given equation in the standard form, divide throughout by x2,
......(1)
....(2)
To remove the first derivative,
or, u = ex elogx = x ex .....(3)
As given,
Therefore the normal form of the given equation is
or, D2v = 0, where D ≡ d / dv
To solve this, the AE is D2 = 0 ⇒ D = 0, 0
∴ v = (c1 + c2x) e0.x = c1 + c2 x ....(4)
Therefore from (3) and (4), the required CS is
y = uv = xex (c1 + c2x)
Example 2: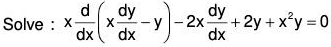
Simplifying the equation and writing in the standard form
....(1)
Now here
To remove the first derivative...(2)
...(3)
and
Therefore the normal formof the given equation is
∴ v = c1 cos (x + c2) ...(5)
Hence by (2) and (5), CS is
y = uv = xc1 cos (x + c2)
Example 3: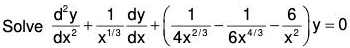
From the equation, it is clear that
...(1)
The remove the first derivatives,.....(2)
Now taking y = uv in the given equation, by (1) and (3), its normal form will be...(4)
(4) is a homogeneous equation therefore to solve this, take x = ez, D = d / dz
D(D - 1) v - 6 v = 0 ⇒ (D2 - D - 6) v = 0
AE is D2 - D - 6 = 0 ⇒ (D + 2) (D - 3) = 0 ⇒ D = - 2,3
Therefore the solution is v = c1e-2z + c2e3z = c1x-2 + c2x3 ....(5)
Hence by (2) and (5), the required CS is.....(5)
Example 4: 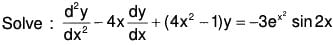
To remove the first derivative....(2)
Let CS of the given equation be y = uv, then its normal form will be...(4)
or, (D2 + 1) v = -3 sin 2x
Its AE is D2 + 1 = 0 ⇒ D = ± i
Therefore CF = c1 cos x + c2 sin x
Therefore the solution is v = c1 cos x + c2 sin x + sin 2x
From (2) and (5), the required CS is y = u v
Method of changing the independent variable
The linear equation of second order in the standard form is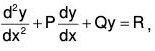 ....(1)
....(1)
where P, Q and R are functions of the variable x.
Changing the independent variable x to z by the substitution z = f(x)
By differential calculus,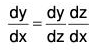 .....(i)
.....(i)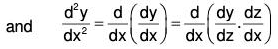
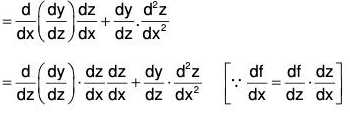
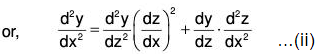
Using (i) and (ii) in (1), we have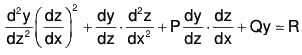
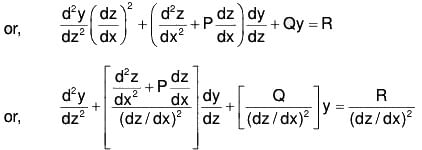
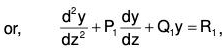 ....(2)
....(2)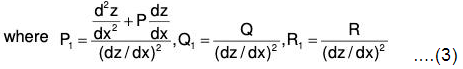
Here P1, Q1 and R1 are all functions of x but can be changed into functions of z by the relation z = f(x).
Selection of the Variable z
Here z should be chosen in such a manner that (2) can be easily integrated to give the solution. For this, if Q1 = constant, then P will also become constant and (2) can be integrated easily. Since z is arbitrary, therefore this can be chosen in such a manner that it satisfies the given condition.
We choose z so that the coefficient of dy/dz become zero.
Case I. If P1 = 0, then (2) will be of the form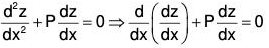

Therefore (2) reduces to 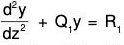 ....(4)
....(4)
(a) Now if Q1 = constant, then (4) will be linear equation and can be solved.
(b) If Q1 = constant / z2, then (4) will be non-homogeneous differential equation of variable coefficients and can be solved by the earlier methods.
Case II. If Q1 = a2, then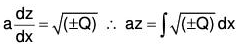
Therefore (2) will be of the form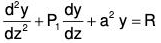
Now if P1 is a constant, then the equation can be easily solved to get the solution.
Remarks : 1. Remember the values of P1, Q1, and R1.
Choose P1 = 0 and Q1 = a2 only and solve.
Example 1: 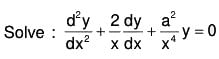
Here,
....(1)
Changing the independent variable x to z, the given equation becomes
Now choose z such that Q = constant = a2 (say)
Therefore the transformed equation isIts AE is D2 + a2 = 0 ⇒ D = ± ai
Therefore the solution is
Example 2: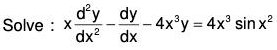
Divide throughout by x, and writing the equation in the standard form
.....(1)
Now choose z such that (dz/dx)2 = 4x2
⇒ dz = 2x dx or z = x2 .....(2)
By the formula,= sin x2 = sin z [by (2)]
and Q, = -1
Change the independent variable x in the given equation to z by (2),
The AE is (D2 - 1) = 0 ⇒ D2 = 1 ⇒ D = ± 1
Therefore the required solution is
Example 3: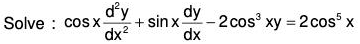
Divide the given equation throughout by cos x and writing in the standard form
Here P = tan x; Q = -2 cos2 x and R = 2 cos4 x
Now choose z such that (dz/dx)2 = 2 cos2 x
dz = √2 cos x dx, Integrating, z = √2 sin x ....(2)
Hence the transformed equation is
Therefore C.F. = c1ez + c2e-z ......(i)[by binomial theorem]
.....(ii)
or, the required CS is y = c1e√2sinx + c2e -√2sinx + sin2 x
Aliter: If z is chosen such that P1 = 0, then
Integrating, dz/dx = cosx, Also z = sin x
Therefore Q1 = -2 and R1 = 2 cos2 x
Then the transformed equation is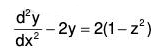
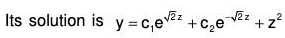
There fore required CS is 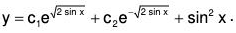
Example 4: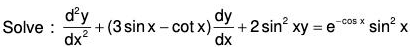
Here , P = 3 sin x - cot x; Q = 2 sin2 x; R = e-cos x sin2 x .....(1)
To change x to z, choose z such that Q1 = a2 = 2 (say)
Therefore dz/dx = sin x or z = -cosx
There fore the transformed equation is.....(4)
or, (D2 + 3D + 2) y = ez
The AE is D2 + 3D + 2 = 0 ⇒ D = -1, -2
Therefore C.F. = c1e-z + c2e-2z ....(i)
The Wronskian Function
Let y1(x) and y2(x) be two solutions of the second order differential equation a0(x) y”(x) + a1(x) y’(x) + a2(x) y(x) = 0
Then the wronskian of y1(x) and y2(x) is denoted and defined as the determinant.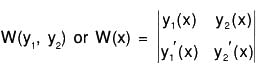
The Wronskian of n functions
Let y1(x), y2(x)..... ,yn(x) be n solutions of (dny/dxn) + P1(dn-1y/dxn-1) + ...+ Pny = 0 of. Then the Wronskian of y1(x), y2(x),...yn(x) is denoted by W(y1,y2,...yn) or W (x) and defined by the determinant.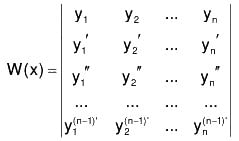
Abel’s Formula
Let y1(x) and y2(x) be two solutions of
y" + p(x)y' + q(x)y = 0, ...(1)
and let W (x) = y1 (x) y2’ (x) - y1’(x) y2(x), .......(2)
be their Wronskian. We can compute the derivative W’(x) as
W’(x) = y1’ (x) y2’’(x) + y1’’(x) y2” (x) - y1’’(x) y2(x) - y1’(x) y2’(x)
= y1(x) y2”(x) - y1”(x) y2(x) ....(3)
Since y1 and y2 are solutions of (1), we have
y1” (x) = -p(x) y1’(x) - q (x)y1(x),
and y2’’(x) = - p (x) y2’(x) - q (x) y2(x), ...(4)
and substituting these into (3), we get
W’(x) = y1(x) [-p(x)y2’(x) - q(x)y2(x)] - [-p(x)y1’(x) - q(x)y1(x)]y2(x)
= -P(x)y1(x)y2’(x) - q(x)y1(x)y2(x) + p(x)y1’(x)y2(x) + q(x)y1(x)y2(x)
= -P(x)y1(x)y2’(x) + p(x)y1’(x)y2(x) .....(5)
= -p(x)W(x).
In other words, the Wronskian satisfies the first order linear equation
W ’(x) + p (x)W (x) = 0. . . . (6)
This fact is known as Abel’s theorem. We can easily solve (6), and derive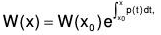 .....(7)
.....(7)
the formula known as Abel’s formula or Abel’s identity. In particular, if the coefficient p(x) is constant, then
W(x) = W(x0)e(x - x0)p .....(8)
An important consequence of Abel’s formula is that the Wronskian of two solutions o/(1) is either zero everywhere, or nowhere zero.
Example: We know that y1(x) = cos x and y2(x) = sin x are solutions to y" + y = 0. Since p = 0 in this case , in light of Abel’s formula, we see Wronskian W(x) of y1 and y2 must be a constant. We confirm it by explicit computations:
W(x) = cos x(sin x)’ - (cos x)’ sin x = cos2 x + sin2 x = 1. ...(9)
Example: The functions y1(x) = ex and y2(x) = xex are solutions to y” - 2y’ + y = 0. Since p = -2, we have W(x) = ce2x for some constantc. Explicit computation gives
W(x) = ex(xex)’ - (ex)’ex = ex(ex + xex) - xe2x = e2x, ....(10)
so c = 1.
Method of Variation of Parameters
Consider the second order non-homogeneous linear equation
a0(x)y” + a1(x)y' + a2(x)y = r(x), a0(x) ≠ 0 .......(1)
We shall discuss a general method of solution, called the method of variation of parameters, which can always be used to find a particular integral whenever we have the complementary function of the equation
a0(x)y” + a1(x)y' + a2(x)y = 0, a0(x) ≠ 0 ......(2)
Using the methods given in the previous section, we can find two linearly independent solutions y1(x) and y2(x) of the equation (2). The complementary function is given by
yc(x) = Ay1(x) + By2(x) ......(3)
where A and B are arbitrary constants. The idea behind the method of variation of parameters is to vary the parameters A and B. That is, we assume A and B to be functions of x and determine A(x), B(x) such that
y(x) = A(x) y1(x) + B(x) y2(x) .....(4)
is the general solution of Eq.(1). Now, y(x) contains two functions A(x) and B(x) which are to be determined. Therefore, we need two equations to determine them. One equation is obtained by substituting y(x) from Eq.(4) in Eq.(1). The determination of the second is at our disposal. This equation is chosen such that the determination of A(x) and B(x) is simple. Differentiating Eq.(1), we obtain
y’(x) = A’y1 + Ay1’ + B’y2 + By2’ = (A’y1 + B’y2) + (Ay1’ + By2’) ......(5)
If we differentiate this equation again, then the equation would contain the second derivatives A” and B” of the unknown functions. In order that these derivatives are not used, we set in Eq.(5)
A’y1 + B’y2 = 0 ........(6)
which gives us the second equation to determine A(x) and B(x). Now, differentiating y’(x) = Ay1’ + By2’ we obtain
y”(x) + Ay1’’ + A’y1’ + By2’’ + B’y2’ ...(7)
Substituting the expressions for y(x), y’(x) and y"(x) in Eq.(1), we obtain
a0(x)[Ay1” + A’y1’ + By2’’ + B’y2’] + a1(x)[Ay1’ + By2’] + a2(x)[Ay1 + By2] = r(x)
or a0(x)[A’y1’ + B’y2'] + A[a0(x)y1” + a1(x) y1’ + a2(x)y1] + B[a0(x)y2” + a1(x)y2’ + a2(x)y2] = r(x).
Since, y1(x) and y2(x) are the solutions of the homogeneous equation (2), we obtain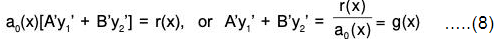
Since a0(x) ≠ 0 on the given interval I, g(x) is continuous on I. Solving the equations
A’y1 + B’y2 = 0
A’y1’ + B’y2’ = g(x),
we obtain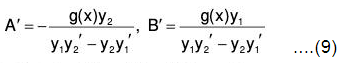
We note that the Wronskian W(y1, y2) is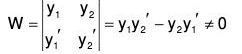
Since y1, y2 are the linearly independent solutions of the homogeneous equation. Hence, we can write Eqs.(9) as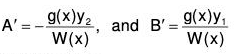 ....(10)
....(10)
Integrating, we obtain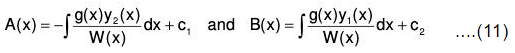
Substituting in Eq.(4), we obtain the general solution which contains two arbitrary constants. If we do not add the arbitrary constants while carrying out integrations of Eqs.(10), then we obtain the particular solution as
yp(x) = A(x)y1(x) + B(x)y2(x), which does not contain any arbitrary constants.
The general solution is given by y(x) = yc(x) + yp(x).
The method is applicable both for constant coefficient and variable coefficient problems. The method can also be easily extended to equations of any order. At each differentiation step, we set the part containing the derivatives of the unknown functions to zero, until we arrive at the final substitution step. For example, consider the third order equation
a0(x)y”’ + a1(x)y" + a2(x)y’ + a3(x)y = r(x), a0(x) ≠ 0 ...(12)
The complementary function is
y(x) = Ay1(x) + By2(x) + Cy3(x)
where y1, y2, y3 are the linearly independent solutions of the corresponding homogeneous equation and A, B, C are arbitrary constants. We assume the solution as
y(x) = A(x) y1(x) + B(x) y2(x) + C(x) y3(x) ........(13)
Following the procedure discussed earlier, we obtain the required equations for determining A(x), B(x) and C(x) as
A’(x)y1 + B’(x)y2 + C’(x)y3 = 0
A’(x)y1’ + B’(x)y2’ + C’(x)y3’ = 0
and A'(x)y1” + B’(x)y2” + C’(x)y3” = r(x)/a0(x) = g(x) .....(14)
The determinant of the coefficient matrix is the Wronskian W(y1, y2, y3) ≠ 0. We determine A(x), B(x), C(x) and substitute in Eq.(13) to obtain the general solution.
Example 1: Find the general solution of the equation y” + 3y’ + 2y = 2ex, using the method of variation of parameters.
The corresponding homogeneous equation is y” + 3y’ + 2y = 0. The characteristic equation is m2 + 3m + 2 = 0 and its roots are m = -1, -2. Hence, the complementary function is
yc(x) = Ay1(x) + By2(x) = Ae-x + Be-2x
where y1(x) = e-x and y2(x) = e-2x are two linearly independent solutions of the homogeneous equation. Assume the general solution as
y(x) = A(x)e-x + B(x)e-2x
We have g(x) = r(x)/a0(x) = 2ex.
The Wronskian of y1(x), y2(x) is given by
Using Eq.(11), we obtain the solutions for A(x) and B(x) as
The general solution is y(x) = A(x)e-x + B(x)e-2x
Example 2: Solve by the method of variation of parameters :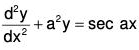
Writing the given equation (D2 + a2) y = sec ax ...(1)
The AE is (D2 + a2) = 0 ⇒ D = ± ai
Therefore the CF of (1) is C.F. = c1 cos ax + c2 sin ax, .....(2)
where c1 and c2 are arbitrary constants.
Let GS of (1) be
y = A cos ax + B sin ax .....(3)
where A and B are to be determined. Choose A and B such that
Using (3) and (6) in (1),....(7)
Multiplying (4) by a sin ax and (7) by cos ax and adding
or dB/dx = 1/a....(8)
....(9)
Therefore using (8) and (9) in (3), the CS is y = A cos ax + B sin ax
Example 3: Solve by the method of variation of parameters :
Dividing throughout by x2 and writing it in the normal form
....(1)
By inspection, P + Qx = 0 therefore y = x is a part of CF ....(2)
Again taking y = vx in (1), we have
The AE is D2 - 2D = 0 ⇒ D = 0, 2
Therefore v = c1 + c2e2x ....(3)
Hence CF is
y = vx = c1x + c3x e2x ....(4)
Now let the solution of (1) be
y = Ax + Bxe2x ....(5)
where A and B are functions of x and are given by....(6)
....(7)
Solving (6) and (7),
and
which on integrating,
and
where k1 and k2 are arbitrary constants of integration. Hence CS is
Example 4: Solve by the method of variation of parameters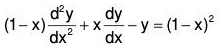
Writing the given equation in the normal form
...(1)
Taking RHS of (1) zero, then
By inspection, P + Qx = 0 ⇒ y = x is a part of CF. ...(2)
Again 1 + P + Q = 0 ⇒ y = ex i s also a part of CF ...(3)
Therefore the solutions
y = c1ex + c2x .......(4)
Now let the solution of (1) be
y = Aex + Bx ......(5)
where A and B are functions of x. Now using the earlier methods, A and B should satisfy the following conditions:
Solving (i) and (ii)
dB/dx =1, integrating, B = x + k1 ......(6)
and dA/dx = -xe-x, integrating A = e-x (x + 1) + k2 .....(7)
Using (6) and (7) in (5), we have the required CS
y = [e-x (x + 1) + k2] ex + (x + k1) x
or, y = k1x + k2ex + (1 + x + x2)
Example 5: 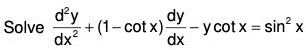
Here 1 - P + Q = 0. Therefore the solution of AE is y = e-x
Now let y = ve-x, then taking R = 0 the given equation reduces to the form
Let dv / dx = p, then
Integrating, log p = log c1 + x + log sin x = log (c1 sin xex)
which is CF of the given equation.
Now solution of (1) be
y = A (sin x - cos x) + Be-x, ...(2)
where A and B are functions of x whose values can be obtained from the following equations.....(3)
Using (5) and (6) in (2), the required CS is obtained.
|
98 videos|34 docs|32 tests
|
FAQs on Differential Equations- II - Mathematics for Competitive Exams
| 1. What is the difference between homogeneous and non-homogeneous linear differential equations? |  |
| 2. What is the Cauchy-Euler equation in differential equations? |  |
| 3. How do you solve linear equations of second order with variable coefficients? |  |
| 4. What is the method of variation of parameters in differential equations? |  |
| 5. What is the significance of the method of variation of parameters in IIT JAM exam? |  |