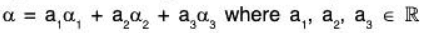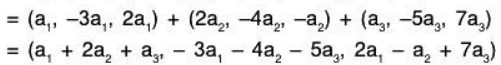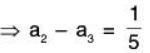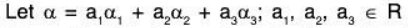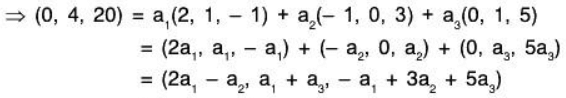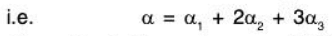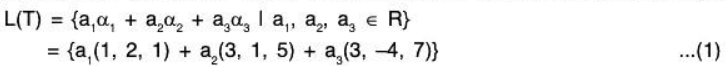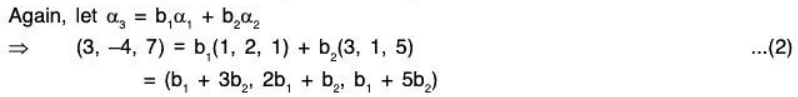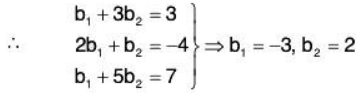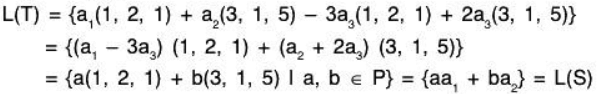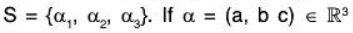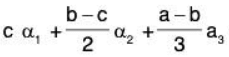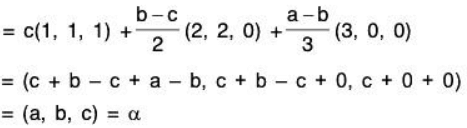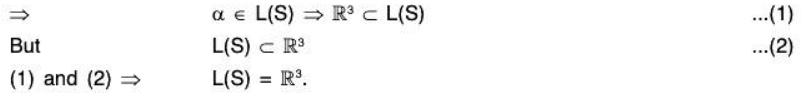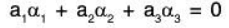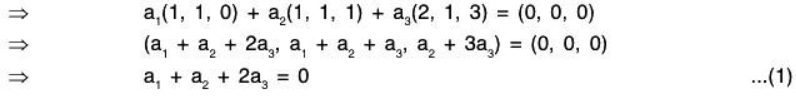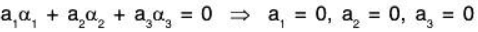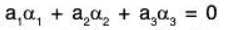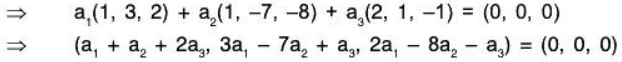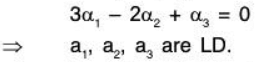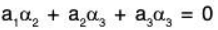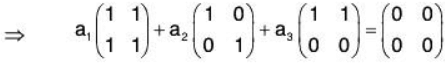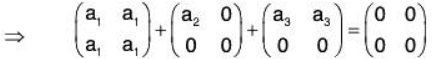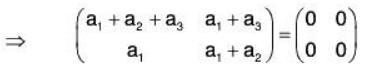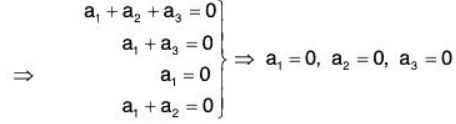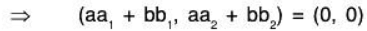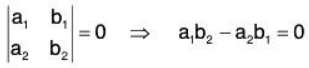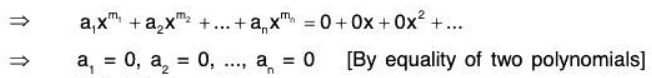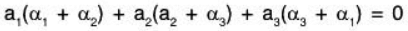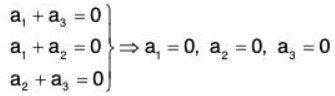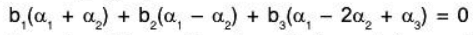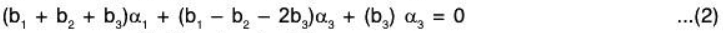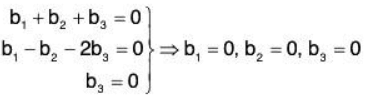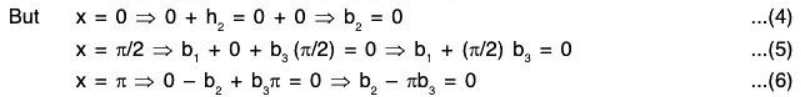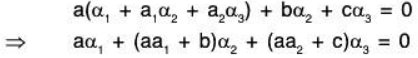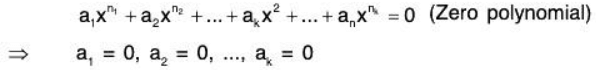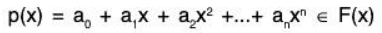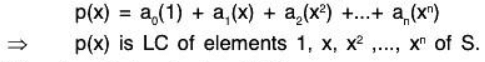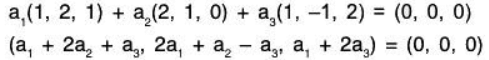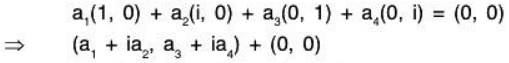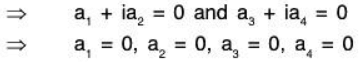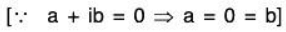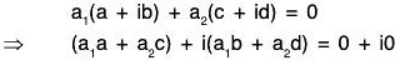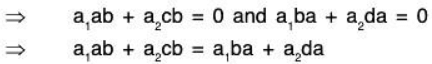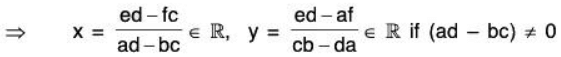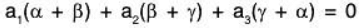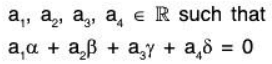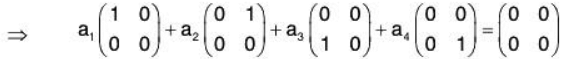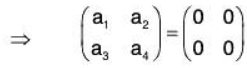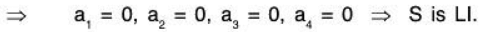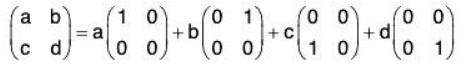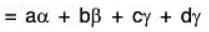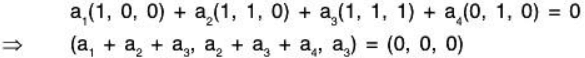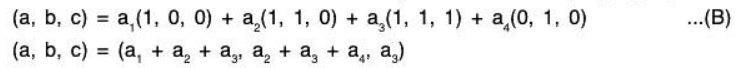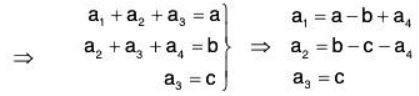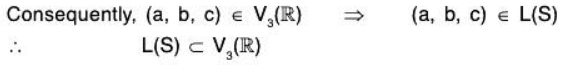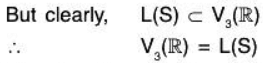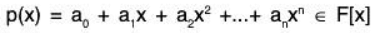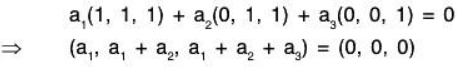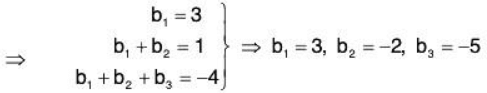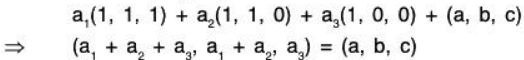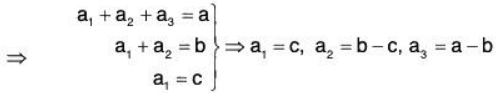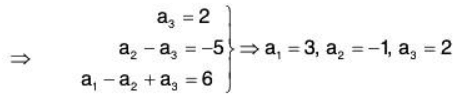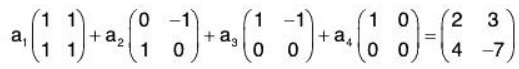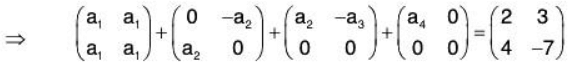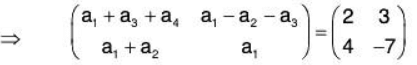Vector Space & Linear Transformation- 2 | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Linear Combination |

|
| Subspaces |

|
| Linear Dependence and Independence |

|
| Basis and Dimension |

|
Linear Combination
Let V be a vector space over a field K. A vector v in V is a linear combination of vectors u1, u2, .... , um in V if the exist scalars a1, a2, ...... am in K such that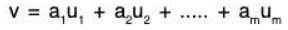
Alternatively, v is a linear combination of u1, u2, .... , um if there is a solution to the vector equation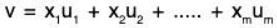
where x1, x2, ..... xm are unknown scalars.
Example: (Linear Combinations in ℝn) Suppose we want to express v = (3, 7, - 4) in ℝ3 as a linear combination of the vectors
u1 = (1, 2, 3), u2 = (2, 3, 7) u3 = (3, 5, 6)
We seek scalar x, y, z such that v = xu1 + yu2 + zu3; that is,
(For notational convenience, we have written the vectors in ℝ3 as columns, because it is then easier to find the equivalent system of linear equations.) Reducing the system to echelon form yields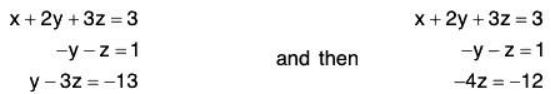
Back-substitution yields the solution
x = 2, y = - 4 , z = 3
Thus v = 2u1 — 4u2 + 3u3.
Spanning Set
Let V be a vector space over K. Vectors u1, u2, .... , um in V are said to span V or to form a spanning set of V if every v in V is a linear combination of the vectors u1, u2, .... , um that is, if there exist scalars a1, a2, ...... am in K such that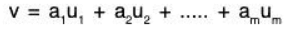
The following remarks follow directly from the definition.
Remark
- Suppose u1, u2, .... , um span V. Then, for any vector w, the w,u1, u2, .... , um also spans V.
- Suppose u1, u2, .... , um span V and suppose uk is a linear combination of some of the other u’s. Then u’s without uk also span V.
- Suppose u1, u2, .... , um span V and suppose one of the u’s is the zero vector. Then the u’s without the zero vector also span V.
Example: Consider the vector space V = ℝ3.
(a) We claim that the following vectors form a spanning set of ℝ3 :
e1 = (1,0,0), e2 = (0,1,0), e3 = (0, 0, 1)
Specifically, if v = (a, b, c) is any vector in ℝ3,
then v = ae1 + be2 + ce3
For example, v = (5, - 6, 2) = - 5e1 - 6e2 + 2e3.
Note : L(ϕ) = {0}
Example: If S = {(1, 0, 0)} ⊂ V3(ℝ),
then L(S) = {(a, 0, 0) I a ∈ ℝ}
which is the set of all points of x-axis.
Example: If S = {(1, 0, 0), (0, 1, 0)} ⊂ V3(ℝ), then
L(S) = {(a, b, 0) I a, b ∈ ℝ}
which is the set of all points of xy plane.
Example: If S = {(1, 0, 0), (0, 1, 0), (0, 0, 1)} ⊂ V3(ℝ),
then for every vector α = (a, b, c) of V3(ℝ)
(a, b, c) = a(1, 0, 0) + b(0, 1, 0) + c(0, 0, 1)
⇒ (a, b, c) ∈ L(S) ⇒ V3(ℝ) ⊂ L(S)
but L(S)⊂ V3(ℝ)
L(S) = V3(ℝ)
Theorem: The linear span L(S) of any non empty subset S of a vector space V(F) is the smallest subspace of V(F) containing S
i.e., L(S) = {S}
Proof. Let α, β ∈ L(S), then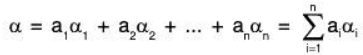
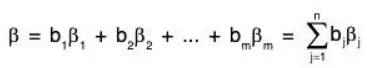
where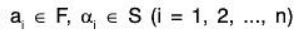
and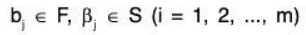
If a, b are any arbitrary elements of the field F, then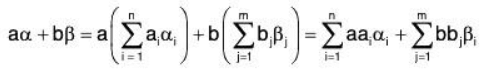
which shows that aα + bβ is a LC of the vectors of finite number of subsets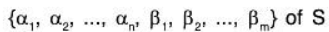
Hence aα + bβ ∈ L(S)
∴ α, β ∈ F and α, β ∈ L(S) ⇒ aα + bβ ∈ L(S)
Therefore L(S) is a subspace of V(F).
Again for every vector α of S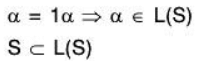
Now let W be any subspace of V containing S(S ⊂ W), then element of L(S) must be in W, for W being subspace, is closed for vector addition and scalar multiplication. Therefore L(S) ⊂ W.
Consequently, L(S) = {S}
i.e. L(S) is the smallest subspace of V containing S.
Linear Sum of two subspaces
Let W1 and W2 be the two subspaces of V(F). Then the linear sum of the subspaces W1 and W2 is the set of all possible sums (a, + a2), where a, ∈ W. and a2 ∈ W2 The linear sum is denoted by W1 + W2.
Symbolically, W1 + W2 = {α1 + α2 I α1 ∈ W1, α2 ∈ W2}
Since 0 ∈ W1, and 0 ∈ W2, therefore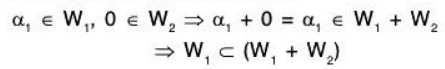
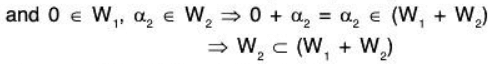
Remark: 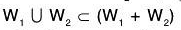
Theorem: The linear sum of two subspaces of a vector space is also a subspace.
Proof: Let W1 and W2 be the two subspaces of V(F).
Let 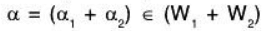 and
and 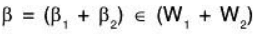
where 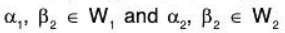
Now since W1 and W2 are two subspaces, therefore
Again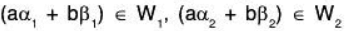
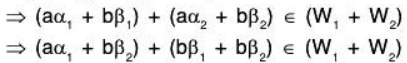
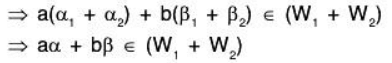
Therefore a, b ∈ F and 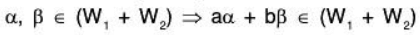
∴ (W1 + W2) is also a subspace of V(F).
Theorem: If W1 and W2 are subspace of a vector space V(F), then their sum is generated by their union i.e.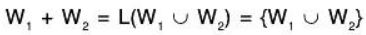
Proof: Since W1 and W2 are the subspaces of V(F), therefore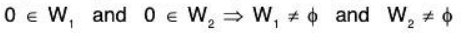
Let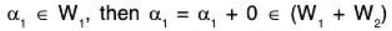
⇒ W1 ⊂ (W1 + W2) ...(1)
Similarly W2 ⊂ (W1 + W2) ...(2)
(1) and (2) ⇒ W1 ∪ W2 ⊂ (W1 + W2) ...(3)
But by theorem (W1 + W2) is a subspace of V(F) containing W1 ∪ W2.
To prove W1 + W2 = L (W1 ∪ W2) :
Let 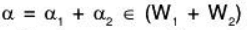 where α1 ∈ W1 and α2 ∈ W2
where α1 ∈ W1 and α2 ∈ W2
then clearly 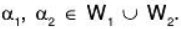
Now since 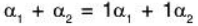
⇒ α1 + α2 can be expressed as a LC of the vectors α1, α2 ∈ W1 ∪ W2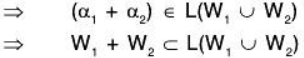 .... (4)
.... (4)
But we know that L(W1 ∪ W2) is the smallest subset of V(F) containing W1 ∪ W2 and by (3)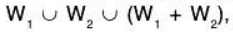
therefore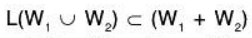 .... (5)
.... (5)
(4) and (5)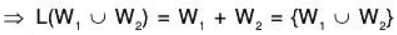
Theorem: If S and T are subsets of a vector space V(F) then:
(a) S ⊂ T u L(S) ⊂ L(T)
(b) S ⊂ L(T) L(S) ⊂ L(T)
(c) L(S ∪ T) ⇒ L(S) + L(T)
(d) S is a subspace of V ⇔ L(S) = S
(e) L{L(S)} = L(S)
Proof:
(a) Let 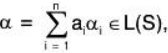 where ai ∈ F and {α1, α2, .... αn} is a finite subset of S.
where ai ∈ F and {α1, α2, .... αn} is a finite subset of S.
Now since S ⊂ T , therefore
S ⊂ T ⇒ ai ⊂ T (i = 1, 2, n)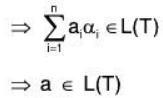
Therefore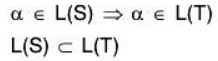
(b) Let 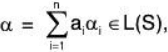 where ai ∈ F and {α1, α2, .... αn} is a finite subset of S.
where ai ∈ F and {α1, α2, .... αn} is a finite subset of S.
Now since S ⊂ L(T) ,
therefore 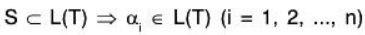


Therefore
(c) Let 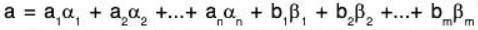 be any element of the set L(S∪ T) where
be any element of the set L(S∪ T) where 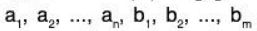 are the elements of the field F and
are the elements of the field F and 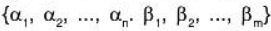 is a limits subset of S ∪ T such that
is a limits subset of S ∪ T such that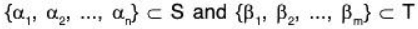
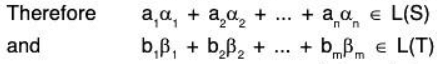
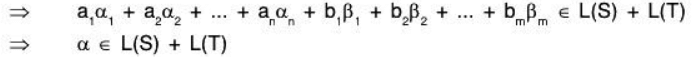
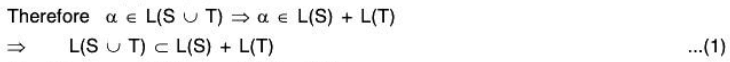
Now let α ± β + γ ∈ L(S) + L(T)
⇒ β ∈ L(S) and γ ∈ L(T)
⇒ β is LC of elements of the finite subset of S and γ is a LC of elements of the finite subset of T
⇒ β + γ is a LC of finite elements of S ∪ T
⇒ β + γ ∈ L(S ∪ T)
⇒ L(S) + L(T) ⊂ L(S ∪ T) ...(2)
Therefore (1) and (2) L(S ∪ T ) = L(S) + L(T)
(d) First suppose S is a subspace of V, then to show that L(S) = S
Let 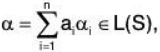 where ai ∈ F and {α1, α2, ..., αn} is a finite subset of S.
where ai ∈ F and {α1, α2, ..., αn} is a finite subset of S.
Now since S is a finite subset of V(F), therefore this is closed for vector addition and scalar and scalar multiplication. Consequently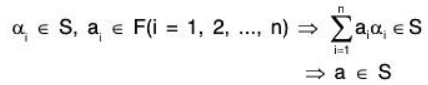
Therefore α ∈ L(S) ⇒ a ∈ S ...(1)
L(S) ⊂ S ...(2)
But in each case, S ⊂ L(S)
Therefore (1) and (2) ⇒ L(S) = S
Conversely: Let L(S) = S, then to show that S is a subspace of V(F). By theorem L(S) is a subspace of V(F), therefore S(= L(S)) will also be subspace of V(F).
(e) Since L(S) is a subspace of V(F), therefore by (d) above,
L{L (S)} = L(S).
Example 1: Is the vector α = (2, -5, 3) <= V3(R), a LC of the following vectors?
α1 = (1, -3, 2), α2 = (2, -4, -1), α3 = (1, -5, 7)
Let
Now (2, - 5 , 3) = a1(1, - 3 , 2) + a2(2, - 4 , - 1 ) + a3(1, - 5 , 7)
(1) and (2)and
(1) and (3)
which is not possible. Therefore equations (1), (2), (3) are inconsistent. Consequently it is not possible to express a is LC of α1, α2, α3.
Example 2: If possible, express the vector 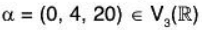 as a LC of the following vectors:
as a LC of the following vectors:
α1 = (2, 1, - 1), α2 = (- 1, 0, 3), α3 = (0, 1, 5)
2a1 - a2 = 0 ...(1)
a1 + a3 = 4 ...(2)
-a1 + 3a2 + 5a3 = 20 ...(3)
Solving (1), (2), (3), we obtain a1 = 1, a2 = 2, a3 = 3 all in the field R.
Therefore vector a can be expressible as a LC of α1, α2, α3
Example 3: In the vector space V3(ℝ), let α1 = (1, 2, 1); α2 = (3, 1,5); α3 = (3, -4, 7). Then prove that the subspaces spanned by S = {α1, α2} and T = {α1, α2, α3} are the same.
Since the linear span L(T) of T is the set of LC of the vectors α1, α2, α3, therefore let
Substituting these values of b1 and b2 in (2), we get(3, -4, 7) = -3(1, 2, 1) + 2(3, 1, 5)
⇒ a3(3, -4, 7) = -3a3(1, 2, 1) + 2a3(3, 1, 5) .... (3)
Now by (1) and (3),
Example 4: Show that the following vectors span the vector space ℝ3: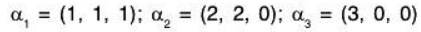
Let
thenare scalars such that
Subspaces
Definition: Let V be a vector space over a field K and let W be a subset of V. Then W is a subspace of V if W is itself a vector space over K with respect to the operations of vector addition and scalar multiplication on V.
Theorem: Suppose W is a subset of a vector space V. Then 1 is a subspace of V if the following two conditions hold :
(a) The zero vector 0 belongs to W.
(b) For every u, v ∈ W, k ∈ K:
- The sum u + v ∈ W.
- The multiple ku ∈ W.
Example: Consider the vector space V = ℝ3.
(a) Let U consist of all vectors in ℝ3 whose entries are equal; that is
U = {(a, b, c) : a = b = c}
For example, (1, 1, 1), (- 3, - 3, - 3), (7, 7, 7), (- 2, - 2, - 2) are vectors in U. Geometrically, U is the line through the origin O and the point (1, 1, 1). Clearly O = (0, 0, 0) belongs to U, because all entries in O are equal. Further, suppose u and v are arbitrary vectors in U, say u = (a, a, a) and v = (b, b, b). Then, for any scalar k ∈ R, the following are also vectors in U : u + v = (a + b, a + b, a + b) and ku = (ka, ka, ka)
Thus, U is a subspace of ℝ3.
Linear Dependence and Independence
Let V be a vector space over a field K. The following defines the notion of linear dependence and independence of vector over K.
Definition: We say that the vectors v1, v2,......vm in V are linearly dependent if there exist scalars a1, a2,......am in K, not all of them 0, such tha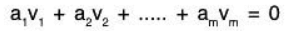
Otherwise, we say that the vectors are linearly independent.
The above definition may be restated as follows. Consider the vector equatio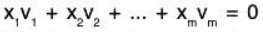 .. (*)
.. (*)
where the x’s are unknown scalars. This equation always has the zero solution x1 = 0, x2 = 0, ..., xm = 0. Suppose this is the only solution; that is, suppose we can show: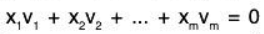 implies
implies 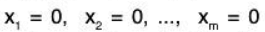
Then the vectors v1, v2,......vm are linearly independent, On the other hand, suppose the equation (*) has a nonzero solution; then the vectors are linearly dependent.
A set S = {v1, v2,......vm} of vectors in V is linearly dependent or independent according to whether the vectors v1, v2,......vm are linearly dependent or independent.
An infinite set S of vectors is linearly dependent or independent according to whether there do or do not exist vectors v1, v2,......vk in S that are linearly dependent.
The following remarks follow directly from the above definition.
Remark: Suppose 0 is one of the vectors v1, v2,......vm, say v1 = 0. Then the vectors must be linearly dependent, because we have the following linear combination where the coefficient of v1 ≠ 0: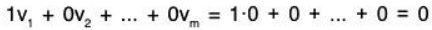
Remark: Suppose v is a nonzero vector. Then v, by itself, is linearly independent, because kv = 0, v ≠ 0 implies k = 0
Remark: Suppose two of the vectors v1, v2,......vm are equal or one is a scalar multiple of the other, say v1 = kv2. Then the vectors must be linearly dependent, because we have the following linear combination where the coefficient of v1 ≠ 0: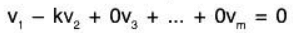
Remark: Two vectors v1 and v2 are linearly dependent if and only if one of them is a multiple of the other.
Remark: If the set {v1,......vm} is linearly independent, then any rearrangement of the vectors  is also linearly independent.
is also linearly independent.
Remark: If a set S of vectors is linearly independent, then any subset of S is linearly independent. Alternatively, if S contains a linearly dependent subset, then S is linearly dependent.
Theorems on Linear Dependence and Independence
Theorem: A set of vectors which contains atleast one zero vector is LD.
Proof: Let S = {α1, α2,......αn} be the set of n vectors of any vector space V(F) in which α1 = 0 and all the remaining are non zero vectors.
Now choose scalars 1, 0, 0, 0, ... (not all zero) so that
1α1 + 0α2 + 0α3 +...+ αn = 0 ..... (1)
Therefore from (1), it is clear that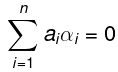
where a, = 1 ∈ F unit element and a1 = 0 ∈ F is zero scalar.
Hence S is LD.
Theorem: Every non-empty subset of a LI set of vectors is also LI.
Proof: Let S = {α1, α2,......αn} be LI set of n vectors of any vector space V(F). Then there exist a1, a2, .... an ∈ F such that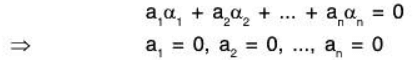
Let S’ = {α1, α2,......αm}, m ≤ n be the non empty subset of the vector set S. Now since α1, α2, ... αn are LI, therefore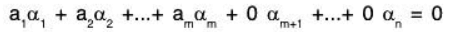
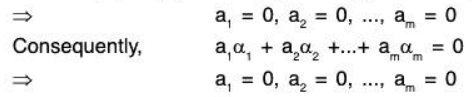
Therefore the subset S’ is also LI.
Theorem: Any superset of a LD set of vectors is also LD.
Proof: Let S = {a1, a2, .... an} be LD set of n vectors of vector space V(F). Then there exist a1, a2, .... an ∈ F (not all zero) such that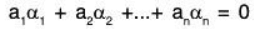 ....(1)
....(1)
Let S’ 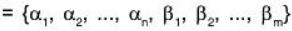 be a super of set S,
be a super of set S,
then by (1),
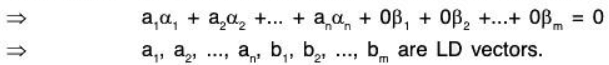
[∵ scalars a1, a2, .... an are not all zero]
⇒ S’ is also LD set.
Theorem: If V(F) is a vector space and S = {α1, α2,......αn} is a subset of some non-zero vectors of V, then S is LD iff some element of S can be expressed as a LC of the others.
Proof: Let S = {α1, α2,......α} be LD. Then there exist a1, a2, .... an ∈ F (not all zero) such that a1α1+ a2α2 + .... + anαn = 0 ...(1)
Let ak ≠ 0, then (1) can be written as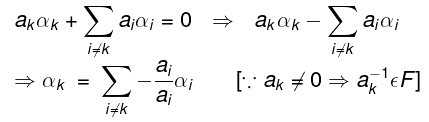
Therefore αk ∈ S is expressible as a LC of the remaining vectors.
Conversely: Let α1 ∈ S be expressible as a LC of the remaining vectors of S. Therefore let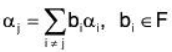
⇒ 
⇒ α1, α2,......αn is LD ( ∵ - 1 ≠ 0)
⇒ S is LD
Theorem: If V(F) is a vector space and S = (α1, α2,......αn) is a subset of some non-zero vectors of V, then S is LD iff some of the vectors of S, say αk where 2 ≤ k ≤ n, can be expressed as a LC of preceding one's.
Proof: Let αk ∈ S be a vector expressible as a LC of the preceding vectors of S.
Therefore let there exist scalars a1, a2, .... ak-1 ∈ F such that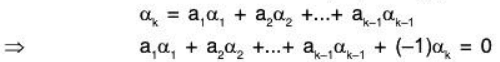
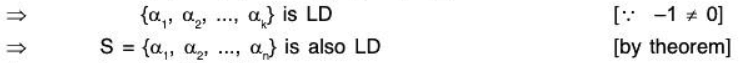
Conversely: Let S be LD.
The set {a1} is clearly LI because a1 ≠ 0
Now consider the set { α1, α2}
If this is LD then there exist a1, a2 ∈ F such that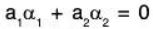 where both a1, a2 are not zero. ... (1)
where both a1, a2 are not zero. ... (1)
But a2 ≠ 0 because
Therefore by (1),
⇒ a2 can be expressed as a LC of its preceding vector α1
Now if the set 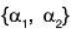 is LI, then we consider the set {α1, α2,α3}
is LI, then we consider the set {α1, α2,α3}
If this is LD then on the above lines, it can be easily shown that α3 can be expressed as a LC of its preceding vectors α1 and α2.
If {α1, α2,α3} is LI, then proceed as above,
Let k ∈ N such that 2 ≤ k ≤ n and set {α1, α2,......αk-1} is LI
Now consider the set {α1, α2,......αk-1,αk }
If this is LD, then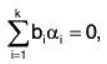 ..... (2)
..... (2)
where bi ∈ F(i = 1, 2, ..., k) are scalars such that atleast one of them is non zero. But aK ≠ 0, because if ak = 0 then set {α1, α2,......αk-1} will be LD which is contrary to our earlier assumption.
Therefore by (2)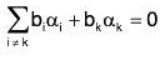

⇒ αk can be expressed as a LC of its preceding vectors.
Example 1: Show that the following vectors of V3(ℝ) are LI :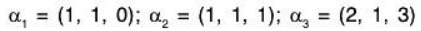
Let a1, a2, a3 ∈ ℝ be the real numbers such that
From (1) and (2), a3 = 0, then by (3), a2 = 0
Now using these in (2), we obtain a2 = 0
Therefore
Therefore the given vectors α1, α2, α3 are LI
Example 2: The following vectors of V3(ℝ) are LD :
a1 = (1, 3, 2); a2 = (1, -7, -8); a3 = (2, 1, -1)
Let a1, a2, a3 ∈ ℝ be real numbers such that
Therefore a1= 3, a2= -2, a3 = 1 is a non zero solution of the above equations. Consequently,
Example 3: Show that the following matrices in the vector space M(R) of all 2 * 2 matrices are LI: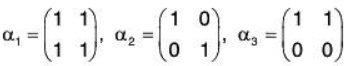
Let
such that
Consequently the given matrices are LI.
Example 4: Show that the vectors 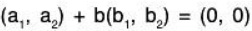
⇒ aa1 + bb1 = 0 .... (1)
aa2 + bb2 = 0 ... (2)
The necessary and sufficient conditions for the existence of the non zero solution of (1) and (2) are:
⇒ The given vectors will be LD iff a1b2 - a2b1 = 0
Example 5: Show that in the vector space V(F) of all polynomials over a field F, the infinite set S = {1, x, x2, x3, ...} is LI.
Let
be the finite subset of the given set S where m1, m2, .... mn are non zero integers.
Let a1, a2, ..., an ∈ F such that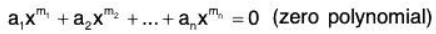
⇒ Sn is LI.
⇒ Every finite subset of S is LI
⇒ S is also LI.
Example 6: If α1, α2, α3 are LI vectors in a vector space V(ℂ), then show that the following vectors are also LI: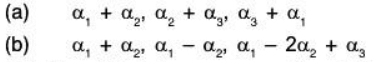
(a) Let a1, a2, a3 ∈ ℂ such that
.... (1)
But α1, α2, α3 are LI, therefore by (1)
Consequently the vectors α1 + α2, α2 + α3, α3 + α1 are also LI.
(b) Again let b1, b2, b3 ∈ ℂ such that
But α1, α2, α3 are LI, therefore by (2)
Consequently the vectorsare also LI.
Example 7: If V be the vector space of all functions defined from ℝ to ℝ; then show that f, g, h ∈ V are LI where:
(a) f(x) = e2x, g(x) = x2, h(x) = x
(b) f(x) = sin x, g(x) = cos x, h(x) = x
(a) Let there exist a1, a2, a3 ∈ ℝ exist such that
a1f + a2g + a3h = 0, where 0 is zero function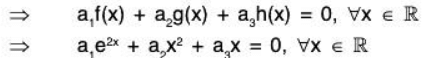
but
From (1), (2), (3), a1 = 0, a2 = 0, a3 = 0
⇒ f, g, h are LI.(a) Let there exist b1, b2, b3 ∈ ℝ exist such that
b1f + b2g + b3h = 0, where 0 is zero function
From (4), (5), (6), b1 = 0, b2 = 0, b3 = 0
⇒ f, g, h are LI.
Example 8: α1, α2, α3 are vectors of V(F ) and a1, a2 ∈ F, then show that the set {α1, α2, α3} is L D if the set {α1 + a1α2 + a2α3, α2, α3}
Let {α1 + a1α2 + a2α3, α2, α3} be a LD set, then there exist a, b, c ∈ F (not all zero) such that
Now if in the above relation (1) if all the coefficients of the vectors α1, α2, α3 are not zero, then the set {α1, α2, α3} will also be LD.
If a ≠ 0, then for any value of b and c, the set {α1, α2, α3} will be LD.
If a = 0, then at least one of b and c will not be zero,
(because if all the three are zero, then the other set will not be LD).Consequently, at least one of the coefficient (aa1 + b) and (aa2 + c) will not be zero.
Therefore the set {α1, α2, α3} will be LD.From the above discussion, it is clear that if the set {α1 + a1α2 + a2α3, α2, α3} is LD, then the set {α1, α2, α3} will always be LD.
Example : (a) Let u = (1, 1, 0), v = (1, 3, 2), w = (4, 9, 5). Then u, v, w are linearly dependent, because 3u + 5v - 2w = (1, 1, 0) + 5(1, 3, 2) - 2(4, 9, 5) = (0, 0, 0) = 0
(b) We show that the vectors u = (1, 2, 3), v = (2, 5, 7), w = (1, 3, 5) are linearly independent. We form the vector equation xu + yv + zw = 0, where x, y, z are unknown scalars. This yields
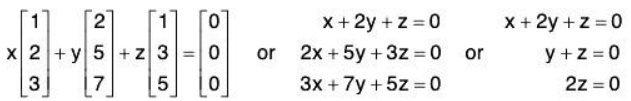
Back-substitution yields x = 0, y = 0, z = 0. We have shown that xu + yv + zw = 0 implies x = 0, y = 0, z = 0
Accordingly, u, v, w are linearly independent.
Lemma: Suppose two or more nonzero vectors v1, v2, ......, vm are linearly dependent. Then one of the vectors is a linear combination of the preceding vectors; that is, there exists k > 1 such that
vk = c1v1 + c2v2 + ... + ck-1vk-1,
Theorem: The nonzero rows of a matrix in echelon form are linearly independent.
Proof: Every non-zero row of a matrix in reduced row-echelon form contains a leading 1, and the other entries in that column are zeroes. Then any linear combination of those other non-zero rows must contain a zero in that position, so the original non-zero row cannot be a linear combination of those other rows. This is true no matter which non-zero row you start with, so the non-zero rows of the matrix must be linearly independent.
Basis and Dimension
Basis of a Vector Space:
Definition: Any subset of S of a vector space V(F) is called basis of V(F), if(i) S is LI and
(ii) S generates V i.e., V = L(S)
i.e. each vector of V is a LC of a finite number of elements of S.
Therefore any LI subset of V which generates V is a basis of V.
Remark:
- Zero vector can not be an element of a basis because then the vectors of the basis will not be LI.
- There may exist a number of bases for a given vector space.
Examples of Bases
Example 1: (Finite Basis) Let Vn(F) be a vector space, then S = {e1, e2,....., en} is a basis of Vn(F), where e1 = (1, 0, 0, .... 0); e2 = (0, 1, 0 0);....., en = (0, 0, 0, 1).
Earlier we have already proved that S is LI.
Again for every vector a = (a1, a2,....., an) of Vn,
there exist a1, a2,....., an ∈ F
such that a = a1e1 + a2e2 +...+ anen
⇒ each vector of Vn is a LC of elements of S.Therefore S is the basis of the vectors space Vn(F).
Remarks:
- The above basis of Vn(F) is called the Standard basis.
- The standard basis of V2(F) = {(1, 0), (0, 1)}
- The standard basis of V3(F) = {(1, 0, 0); (0, 1, 0); (0, 0, 1)} etc.
Example 2: (Finite basis) Every vector space F(F) has a basis {1} where 1 ∈ F is unit element.
Clearly, the set {1} has a non zero element only.
Therefore {1} is LI.
Again for every a ∈ F, a = a1 i.e.
every element of F is LC of {1}.
Consequently {1} is a basis of F(F).Remark: Corresponding to every non zero element a ∈ F, {a} is a basis of F(F)
Example 3: (Infinite basis) : Let F[x] be the vector space of all polynomials over the field F. Then the set S = {1, x, x2, ..., xn, ...} is a basis of F[x].
Let
be the finite subset of the set S and a1, a2,....., ak ∈ F Such that
⇒ S’ is LI.
⇒ every finite subset of S is LI
⇒ S is also LI.
Now we will show that S generate F(x) i.e. every element (Polynomial) of F(x) can be expressed as a LC of finite number of elements of F.
Let
Then there exist a0, a1, a2,....., ak ∈ F such that
Therefore S is a basis of F[x].Remark: F[x] has no finite basis.
Dimension of a Vector Space
Definition: The number of elements in the finite basis of a vector space V(F) is called the dimension of the vector space V(F).
The dimension of the vector space V(F) is denoted by dim V or Dim V.
If dim V = n, then V is called n-dimensional vector space.
Remark: The dimension of the zero space {0} is taken as zero (0).
Example: dim F(F) = 1, because every basis of F is a singleton set containing a nonzero element of F.
Example: dim Vn(F) = n, because {e1, e2,....., en} is a basis of Vn(F) containing n elements.
Similarly, R2(R) = 2, dim R3(R) = 3 etc.
➤ Finite Dimensional Vector Space (FDVS):
Definition: A vector space V(F) is said to be Finite Dimensional Vector Space, if it has a finite basis S such that V = L(S)
i.e. every vector of V is generated by S
The vector space which is not finite dimensional is called infinite dimensional vector space.
Remark: Throughout the text, we shall be using finite dimensional vector spaces (FDVS) only.
Remark: The FDVS is also called finitely generated vector space.
Example: The vector space V3(R) is finite dimensional because S = {(1, 0, 0); (0, 1, 0); (0, 0, 1)} is a finite subset of V3 such that V3 = L(S).
➤ Infinite dimensional vector space:
Definition: The vector space which is not finite dimensional is called infinite dimensional vector space.
Example: The vector space F[x] of all the polynomials in x over any field F is infinite dimensional because there does not exist any finite subset of F[x] which can generate F[x].
Basis of a Finite Dimensional Vector Space:
Theorem: [Existence theorem]:
Every finite dimensional vector space has a basis.
Proof. Let V(F) be a FDVS.
Then by definition, there exist a finite subset
S = α1, α2,......αn of V which spans V i.e. V = L(S).
Without loss of generality, we may suppose that 0 ∉ S because its contribution in the LC of elements of S is zero.
If S is LI, then S itself is a basis of V and the theorem is established.
If S is LD, then by an earlier theorem there exist αk, 2 ≤ k ≤ n is S such that either αk = 0 or αk is a LC of its preceding vectors α1, α2,......αk-1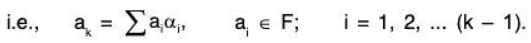
Let us remove αk from S, and denote the remaining set by S1.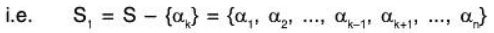
By an earlier theorem S1 also spans V i.e. V = L(S1).
Now if S1 is LI, then it is a basis of V.
But if S1 is LD, then again there exist α1 ∈ S1(l > k) is S1 such that either αi = 0 or αi is a LC of its preceding vectors α1, α2,......αi-1 of S1.
Again let us remove a. from S1 and denote the remaining set by S2 i.e. S2 = S - {αk, αi} which again spans V i.e. V = L(S2).
Proceeding this way after a finite number of steps, either we get a basis for V in the mean while or we are left with the set consisting of a single non zero element which generates V and is LI, thus becomes the basis of V.
Consequently, V(F) has a basis.
Another Form: If a finite set S generates a FDVS V(F), then there exists a subset of S which is the basis of V(F).
Theorem: (Replacement theorem):
Let V(F) be a vector space which is generated by a finite set S = {v1, v2,......vn} of V, then any LI set of V contains not more than n elements.
Proof: Let S = {v1, v2,......vn} generates the vector space V.
S’ = {u1, u2,......un} be any LI set in V, then we have to prove that m ≤ n.
In order to prove this result, it sufficient to show that for m > n, S’ is L.D.
Now since L(S) = V, therefore any v ∈ V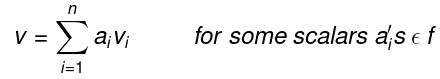
In particular, u1 ∈ S ’⊂ V
⇒ u1 is a LC of v1, v2,......vn
⇒ {u1,v1, v2,......vn} = S1 say) is LD and L(S,) = V (Since the set S, is a spanning set for V)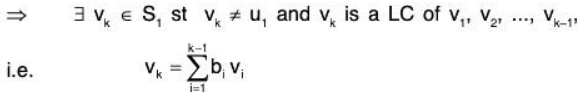
Let us remove this vector vk from S1 and denote the remaining set by S2 i.e.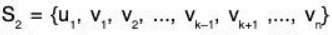
Since L(S1) = V, therefore any v ∈ V is a LC of vectors of S1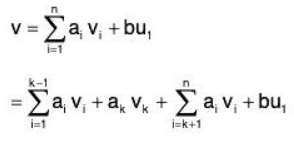
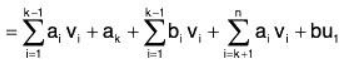
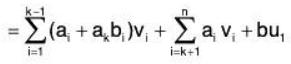
Thus any v ∈ V is a LC of vectors belonging to S2.
∴ L(S2) = V
Next u2 ∈ S’ ⊂ V and S2 generates V therefore u2 is a LC of vectors of S2.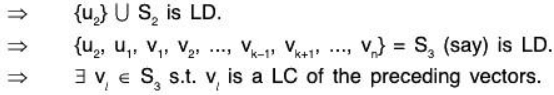
Therefore remove this vector from the set S3 and denote the remaining set by S4 which generates V.
Proceeding in this manner we find that each step consist in the exclusion of a v and the inclusion of u and the resulting set after each step generates V.
If m > n, then after n steps we obtain a set 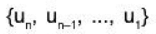
generates V and therefore vn+1, is a LC of the proceeding vectors 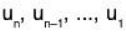 leading us to the conclusion that the set
leading us to the conclusion that the set 
which contradicts the hypothesis that S’ is LI.
Hence m ≥ n i.e. m ≤ n.
Corollary. [Invariance of dimension]:
Any two bases of a FDVS have the same number of elements.
Proof: Let V(F) be a FDVS which has two bases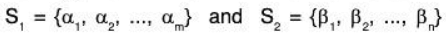
To prove m = n:
Now S1 is basis ⇒ S1 is LI and L(S1) = V ...(i)
and S2 is a basis S2 is LI and L(S2) = V ...(ii)
(i) and (ii) ⇒ L(S1) = V and S2 is LI
Therefore by the above result, m ≤n ...(1)
Also when L(S2) = V and S1 is LI
n ≤ m ...(2)
(1) and (2) ⇒ m = n.
Example: For the vector space V3(F), the sets
B1 ={(1, 0, 0), (0, 1, 0), (0, 0, 1)}
and B2 = {(1, 0, 0), (1, 1, 0), (1, 1, 1)}
are bases as can easily be seen. Both these bases contain the same number of elements i.e. 3.
Some properties of FDVS
Theorem : [Extension Theorem]:
Every LI subset of a FDVS V(F) is either a basis of V or can be extended to form a basis of V.
Proof: Let V(F) be a FDVS whose basis B is 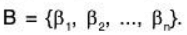
Therefore dim V = n.
Let S = (α1, α2,......αn) be a LI subset of V. Since B is a basis of the space V, therefore B is LI and L(B) = V.
Consider 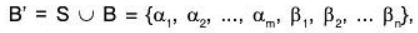
then clearly, L(B’) and B’ are LD because every a can be expressed as a LC of β1, β2,......βn.
Therefore there will exist βk is B' which will be expressible as LC of α1, α2,......αm, β1, β2,......βk-1.
Clearly, βk can not be any of the α1, α2,......αm, because S is LI.
Now remove βk from B’ and denote the remaining set by B”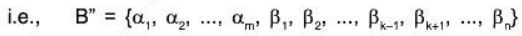
Obviously, L(B”) = V.
Now if B” is LI, then this will be a basis of V and is the required extension set.
If B” is LD, then we repeat the process till after a finite number of steps, we obtain a LI set containing α1, α2,......αm and generating V i.e. basis of V.
Since dim V = n, therefore every basis of V will contain n elements.
Thus exactly (n - m) elements of B will be adjoined to S.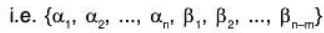 so as to form a basis of V which is the extended form of S. Hence either S is already a basis (when n = m) or it can be extended (when m < n) by adjoining (n - m) elements of B to form the basis of V.
so as to form a basis of V which is the extended form of S. Hence either S is already a basis (when n = m) or it can be extended (when m < n) by adjoining (n - m) elements of B to form the basis of V.
Another form: “Any LI subset of a FDVSV is a part of a basis"
Theorem: In an n-dimensional vector space V(F), any set of (n + 1) or more vectors of V is LD.
Proof: Let V(F) be a vector space and dim V = n.
Therefore every basis of V will contain exactly n elements.
Let S be a subset of V containing (n + 1) or more vectors.
Let, if possible, S is LI, then either it is already a basis or it can be extended to form the basis of V.
Thus in both the cases, the basis will contain (n + 1) or more than (n + 1) vectors which contradicts the hypothesis that V is n-dimensional.
Therefore S is LD and so is every superset of the same.
Theorem: In an n-dimensional vector space V(F), any set of n LI vectors is a basis of V.
Proof: We have dim V = n.
Let S = {α1, α2,......αn} be a LI subset of n-dimensional V(F).
S, being LI subset of V is
either (i) a basis of V,
or (ii) can be extended to form the basis of V.
In case (ii), the basis of V (extended form of S) will contain more than n vectors which contradicts the hypothesis that dim V = n.
Hence the case (i) is true i.e. S is basis.
Theorem: In an n-dimensional finite vector space V(F), any list of n vectors spanning V is a basis.
Proof: We have dim V = n.
Let S = {α1, α2,......αn} be a subset of V such that L(S) = V.
If S is LI, then it will form a basis of V.
IF S is LD, then there exist a proper subset of S’ spanning V and will form a basis of V. This basis S’ will contain less than n elements which contradicts the hypothesis that dim V = n.
Hence S is LI and form a basis of V.
Dimension of a Subspace
Theorem: If W is a subspace of a FDVS V(F), then :
(a) dim W ≤ dim V
(b) W = V ⇔ dim W = dim V.
(c) dim W < dim V, whenever W is a proper subset of V.
Proof: (a) Let V(F) be a finite n-dimensional vector space and W be the subspace of V.
Since dim V = n, therefore any subset of V containing (n + 1) or more vectors is LD,
consequently a LI set of vectors in W contains at the most n elements.
Let S = {α1, α2,......αm }, m ≤ n, be a maximal LI set of vectors in W.
Now if α is any element of W, then the set
S1 = {α1, α2,......αm} is LD (for S being maximum LI vectors of W)
Therefore α ∈ W is a LC of the vectors α1, α2,......αm
⇒ L(S) = W
⇒ S is a basis of the subspace W
⇒ dim W = m, where m ≤ n
⇒ dim W ≤ dim V
(b) (⇒) : Let W = V, then
W = V ⇒ W is a subspace of V and V is a subspace of W.
⇒ dim W ≤ dim V and dim V ≤ dim W [by (a)]
⇒ dim W = dim V.
Conversely (⇐) : Let dim W = dim V = n (say)
Let B = {α1, α2,......αn} be the basis of the space W, then
L(B) = W ...(1)
But B being a LI subset of V containing n vectors, will also generate V i.e.
L(B) = V ...(2)
(1) and (2) ⇒ W = V = L(B)
Therefore W = V ⇔ dim W = dim V.
(c) When W is a proper subspace of V, then there exist a vector α ∈ V but not in W and as such a cannot be expressed as a LC of vectors of W, the basis of W.
Consequently the set {α1, α2,......αm} forms a LI subset of V, therefore the basis of V will contain more than m vectors
∴ dim W < dim V.
Dimension of a Linear Sum
Theorem: If W1 and W2 are two subspaces of a FDVS V(F), then:
dim(W1 + W2) = dim W1 + dim W2 - dim(W1 ∩ W2)
Proof: Let dim(W1 ∩ W2) = k and set S = {γ1, γ2,......, γk} be a basis of W1 ∩ W2, then S ⊂ W1 and S ⊂ W2.
Now since S is LI and S ⊂ W1, therefore by the extension theorem, S can be extended to form the basis of W1.
Let 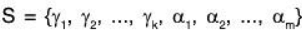 be a basis of W1.
be a basis of W1.
Then dim W, = k + m
Similarly, let 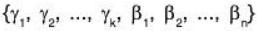 be the basis of W2.
be the basis of W2.
The dim W2 = k + n
∴ dim W1 + dim W2 - dim(W1 ∩ W2) = (k + m) + (k + n ) - k = k + m + n
To prove dim(W1 + W2) = k + m + n :
For this, we shall show that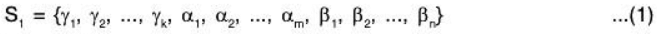
is a basis of (W1 + W2).
Let there exist 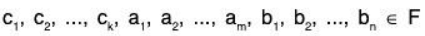 such that
such that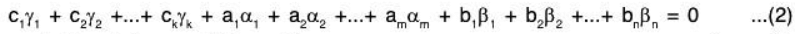
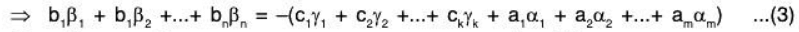
Now since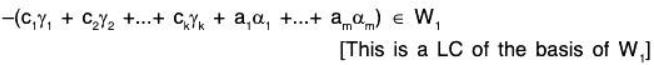
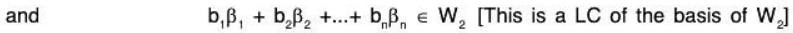
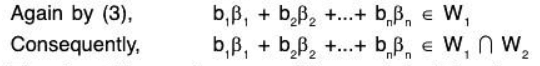
Therefore this can be expressible as a LC of the elements of the basis S of W1 ∩ W2.
Hence let d1, d2, dk ∈ F such that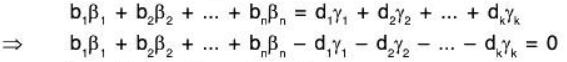
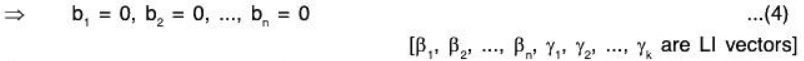 Substituting these values in (1).
Substituting these values in (1).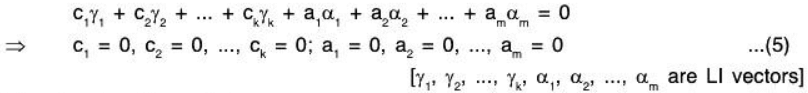 Therefore by (4) and (5),(2)
Therefore by (4) and (5),(2)
⇒ c1 = 0, c2 = 0, ck = 0, a1 = 0, a2 = 0...... am = 0, b1 = 0, b2 = 0, bn = 0
⇒ the set S, is LI.
To show L(S1) = (W1 + W2):
(W1 + W2) is a subspace of V(F) and each element of S1 belongs to (W1 + W2).
Hence L(S,) c (W1 + W2) ...(6)
Again let α ∈ (W1 + W2),
then α = any element of W1 + any element of W2
= LC of elements of a basis of W1 + LC of elements of a basis of W2 = LC of elements of S1.
⇒ α ∈ L(S1)
⇒ (W1 + W2) ⊂ L(S1) ...(7)
Therefore (6) and (7)
⇒ L(S1) = (W1 + W2)
Consequently, S. is a basis of (W1 + W2)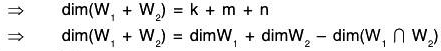
Direct sum of two spaces.
(a) External Direct Sum.Let V(F) and V'(F) be two vector spaces, then the product set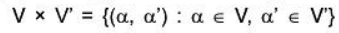
is a vector space over F for the compositions defined as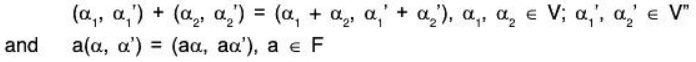
This vector space V * V ’ over F is a called external direct sum o f two vector spaces V(F) and V'(F) and is written as V * V’.
(b) Internal Direct Sum or Direct Sum.
If W1 and W2 be the two subspaces of a vector space V(F), then V(F) is said to be the direct sum of its subspaces W1 and W2, if every α ∈ V can be uniquely expressed a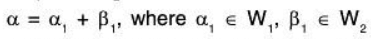
We denote the direct sum of W1 and W2 by W1 ⊕ W2
Then V = W1 ⊕ W2
⇒ v = W1 + W2
Complementary subspaces
If V = W1 ⊕ W2 then W1 and W2 are said to be complementary subspaces i.e. any α ∈ V is uniquely expressible as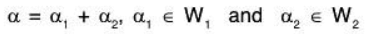
Disjoint subspaces
Two subspaces W1 and W2 of the vector space V(F) are said to be disjoint if W1 ∩ W2 = {0} = zero space.
Theorem: The necessary and sufficient conditions for a vector space V(F) to be a direct sum of its two subspaces W1 and W2 are
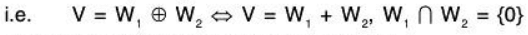 Proof: The Conditions are necessary (⇒):
Proof: The Conditions are necessary (⇒):
Let V = W1 ⊕ W2
By definition of direct sum, each element a ∈ V is uniquely expressed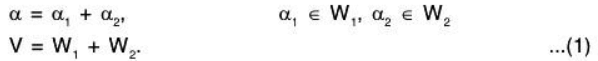
Let, If possible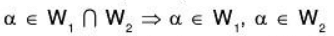
Evidently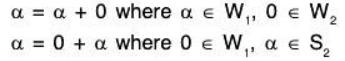
Since the sum for a is unique and hence α = 0But α ∈ W1 ∩ W2 is arbitrary
∴ W1 ∩ W2 = {o}. ...(2)
The conditions are sufficient (⇐):
Let V = W1 + W2 and W1 ∩ W2 = {0}
Let α ∈ V be arbitrary.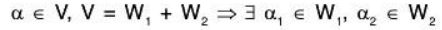
such thatα = α1 + α2
Now we have to show that this representation is unique.
If possible, let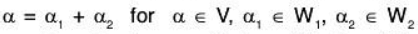
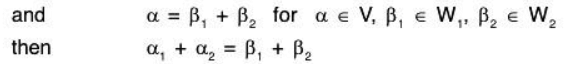
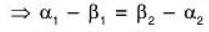
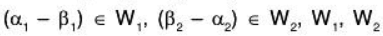
being subspaces of V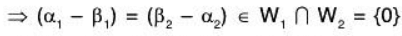 (given)
(given)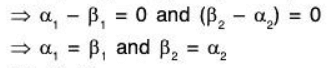
Hence V = W1 ⊕ W2
Dimension of direct sum.
Theorem: If a FDVS V(F) is a direct sum of its two subspaces W1 and W2, then
dim V = dim W1 + dim W2
i.e 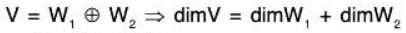 Proof: We have
Proof: We have
V = W1 ⊕ W2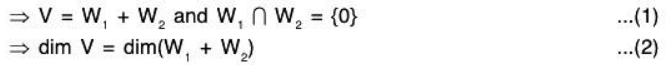
By theorem we have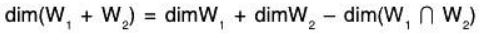 ...(3)
...(3)
Here we haveW1 + W2 =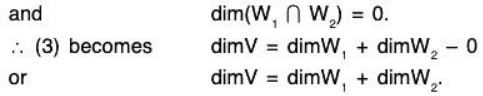
Example 1: Prove that the set S = {(1,2, 1), (2, 1, 0), (1,-1, 2)} forms a basis of the vector space V3(ℝ).
All the 3 elements of S are in V3(ℝ), therefore S ⊂ V3(ℝ).
To show that S is LI:
Let a1, a2, a3 ∈ R such thatBy (1) and (2),
By (1) and (3),
By (3) and (4) and (5),a1 = 0, a2 = 0, a3 = 0
⇒ Vectors of S are LI.
Hence S is a set of 3 LI vectors of V3(ℝ).
Example 2: If V(ℝ) be the vector space of all ordered pairs of complex numbers over the real field R, then prove that the set S = {(1, 0); (i, 0); (0, 1), (0, i)} is a basis of V(ℝ). To show that S is LI:
Let a1, a2, a3, a4 ∈ R Such that
⇒ S is LI.
To show that V = L(S):
Let α = (a + ib, c + id) ∈ V, where a, b, c, d ∈ R, then
α = (a + ib, c + id)= a(1, 0) + b(i, 0) + c(0, 1) + d(0, i)
⇒ α ∈ V is LC of elements of S
⇒ V = L(S).
Hence S is a basis of V(R).
Example 3: Prove that the set S = {a + ib, c + id} is a basis set of the vector space ℂ(ℝ) iff (ad - be) ≠ 0.
To show that S is LI :
Let a1, a2 ∈ ℝ such that
...(1)
Again when a2 = 0 then by (1), a1 = 0
Therefore S will be LI.
Therefore S is LI if (be - ad) ≠ 0.
To show that C(R) = L(S).Let α = e + if ∈ ℂ(ℝ) such that
α = e + if = x(a + ib) + y(c + id), where x, y ∈ E
⇒ e = if = (xa + yc) + i(xb + yd)
⇒ c = ax + cy, f = bx + dyTherefore each element of ℂ(ℝ) can be expressed as LC of elements of S if (ad - be) ≠ 0⇒ ℂ(ℝ) = L(S) if (ad - be) ≠ 0
Hence S is a basis of ℂ(ℝ) iff (ad - be) ≠ 0
Example 4: If the set S = {α, β, γ} be a basis of the vector space V3(ℝ), then prove that the set 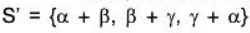 will also be a basis of V3(ℝ).
will also be a basis of V3(ℝ).
Since there are 3 elements in the basis S of V3(ℝ).
Therefore the set of any 3 LI vectors of V3(ℝ) will be its basis.To show that S’ is LI :
Let a1, a2, a3 ∈ ℝ such that
...(1)
But α, β, γ are LI, therefore
Therefore S’ is also LI. Now since the basis S of V3(ℝ) contains 3 vectors, therefore S’ is a subset of 3 LI vectors. As such S’ will also be basis of V3(ℝ).
Example 5: Show that the dimension of the vector space V(ℝ) of all 2 * 2 real matrices is 4.
Let us consider the following 4 matrices of the order 2*2.
We will show that their set
is LI and generates V(ℝ)
Let
Again for any element
of V, there exist a, b, c, d ∈ ℝ such that
⇒ each element of V is a LC of elements of S⇒ V = L(S)
⇒ S is a basis of V(ℝ).But the number of elements in S is 4, therefore dim V = 4.
Example 6: Show that the set S = {(1, 0, 0); (1, 1, 0); (1, 1, 1); (0, 1, 0)} spans the vector spaceV3(ℝ) but is not a basis set.
Here we will show that S is not LI, yet V3(ℝ) = L(S).
Let a1, a2, a3, a4 ∈ ℝ such that...(A)
The above system (A) has 4 unknown quantities and 3 equations.
Therefore there exist a non zero solution. Consequently, S is not LI.
Hence S’ is not a basis set of V3(ℝ).
Again suppose that for any vector (a, b, c) of V3(ℝ), there exist a1, a2, a3, a4 ∈ ℝ such that
Therefore for the relation (B), non zero values of a1, a2, a3, a4 exist.
Therefore the set S spans V3(ℝ), but it is not a basis set. Hence Proved.
Example 7: Show that the set S = {1, x, x2, ..., xn} is a basis of the vector space F[x] of all polynomials of degree at most n, over the field ℝ of real numbers.
To show that S is LI:
Let a1, a2, a3, a4 ∈ ℝ such that(zero polynomial)
Again F[x] = L(S),
since
⇒ p(x) is a LC of elements 1, x, x2, ..., xn of S
Therefore S is a basis of F[x].
First we state two equivalent ways to define a basis of a vector space V.
Definition A: A set S = {u1, u2, ..., un} of vectors is a basis of V if it has the following two properties: (1) S is linearly independent. (2) S spans V.
Definition B: A set S = {u1, u2, ..., un} of vectors is a basis of V if every v e V can be written uniquely as a linear combination of the basis vectors.
Theorem: Let V be a vector space such that one basis has m elements and another basis has n elements. Then m = n.
A vector space V is said to be of finite dimension n or n-dimensional, written
dim V = n
If V has a basis with n elements. Theorem tells us that all bases of V have the same number of elements, so this definition is well defined.
The vector space {0} is defined to have dimension 0.
Suppose a vector space V does not have a finite basis. Then V is said to be of infinite dimension or to be infinite-dimensional.
Lemma: Suppose {v1, v2 ..... vn} spans V, and suppose {w1, w2, ..., wm} is linearly independent.
Then m ≤ n, and V is spanned by a set of the form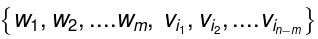
➤ Examples of Bases
Vector space Kn: Consider the following n vectors in Kn:
e1 = (1, 0, 0, 0, .... 0, 0), e2 = (0, 1, 0, 0, .... 0, 0 ) ...... en = (0, 0 , 0 , 0 ...... 0 , 1)
These vectors are linearly independent. (For example, they form a matrix in echelon form.)
Furthermore, any vector u = (a1, a2......an) in Kn can be written as a linear combination of the above vectors. Specifically,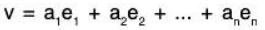
Accordingly, the vectors form a basis of Kn called the usual or standard basis of Kn. Thus (as one might expect), Kn has dimension n. In particular, any other basis of Kn has n elements.
➤ Theorem on Bases
The following three theorems will be used frequently.
Theorem : Let V be a vector space of finite dimension n. Then:
(i) Any n + 1 or more vectors in V are linearly dependent.
The statement dim V = n means there exists a basis {v1, .... vn} for V. Let vn+1 ∈ v\{v1, .... vn}. Then by the definition of a basis, there exist a1, ..., an ∈ F(F being the field over which V is defined) such that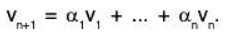
So, {v1, .... vn+1} is linearly dependent.
(ii) Any linearly independent set S = {u1, u2, ...... ,un} with n elements is a basis of V.
We just need to show that S spans V. That is, each elements of V can be expressed as a linear combination of the elements of S. Let w be an element in V. Since S is a maximal linearly independent set, the elements w, u1, u2, ...... ,un are linearly dependent. Hence there exists λ0, λ1, ...... ,λn in K, not all 0K, such that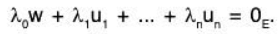
It is clear that 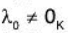 :
:
otherwise the elements u1, u2, ...... ,un would be linearly dependent. Thus, we obtain from (1)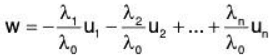
This show that w is a linear combination of the elements of S. Thus, S is a basis of V.
(iii) Any spanning set 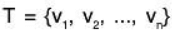 of V with n elements is a basis of V.
of V with n elements is a basis of V.
Suppose 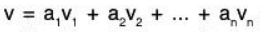 and
and 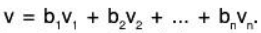 . Subtracting these equations side from side, we obtain
. Subtracting these equations side from side, we obtain 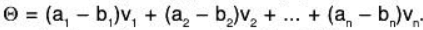
Since the set {v1, v2, ...... ,vn} is linearly independent we have a1 - b1 = 0, which means ai = bi for each i = 1, 2, ..., n.
Hence T is a basis of V.
Theorem: Suppose S spans a vector space V. Then :
(i) Any maximum number of linearly independent vectors in S form a basis of V.
(ii) Suppose one deletes from S every vector that is a linear combination of preceding vectors in S. Then the remaining vectors form a basis of V.
Theorem: Let V be a vector space of finite dimension and let S = {u1, u2, ...... ,un} be a set of linearly independent vectors in V. Then S is part of a basis of V; that is, S may be extended to a basis of V.
Example: (a) The following four vectors in ℝ4 form a matrix in echelon form:
(1, 1, 1, 1), (0, 1, 1, 1), (0, 0, 1, 1), (0, 0, 0, 1)
Thus, the vectors are linearly independent, and, because dim ℝ4 = 4, the four vectors form a basis of ℝ4.
(b) The following n + 1 polynomials in Pn(t) are of increasing degree: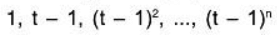
Therefore, no polynomial is a linear combination of preceding polynomials; hence, the polynomials are linear independent. Furthermore, they form a basis of Pn(t), because dim Pn(t) = n + 1.
➤ Quotient Space
Definition :
Let V(F) be a vector space and W be its subspace. Then for any α ∈ V, the set W + α = {w + αlw ∈ W} is called the Right coset of W wrt a in V.
Also the set 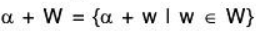 is called the Left coset of W wrt α in V.
is called the Left coset of W wrt α in V.
Since V is an abelian group wrt addition, therefore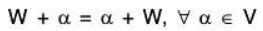
i.e. each right coset of W is equal to its corresponding left cost.
Therefore this is simply called coset.
The set of all the cosets of W in V is denoted by VA/V i.e.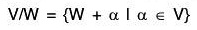
Some properties of cosets:
Let W be a subspace of the vector space V(F), then :
(i) W + 0 = 0 + W = 0, i.e. W is the right as well as left coset of itself.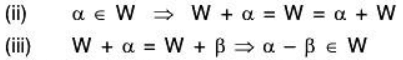 Addition and Scalar multiplication for cosets :If W is a subspace of the vector space V(F), then the addition and scalar multiplication of cosets in V/W are defined as follows:
Addition and Scalar multiplication for cosets :If W is a subspace of the vector space V(F), then the addition and scalar multiplication of cosets in V/W are defined as follows: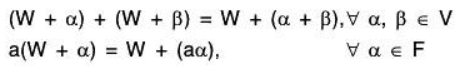
Theorem: If W is a subspace of vector space V(F), then the set V/W of all cosets of W in V is a Vector Space over F for the vector addition and scalar multiplication defined as follows: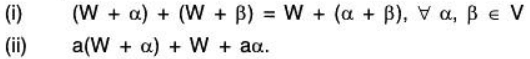
Proof: Vector addition is well defined :
For any α , α', β, β' ∈ V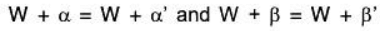
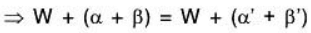
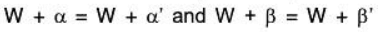
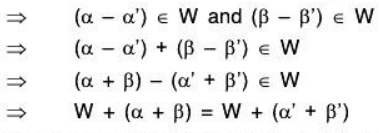
Therefore vector addition is well defined in V/W.
Scalar multiplication is well defined:
For any α ∈ V, α ∈ F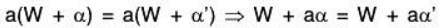
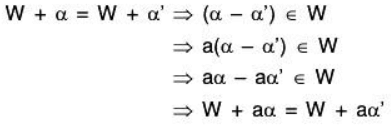
Therefore scalar multiplication is also well defined in V/W.
Again for each α, β ∈ V, a ∈ F
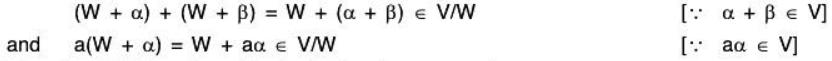 Therefore V/W is closed for both the above operations.
Therefore V/W is closed for both the above operations.
Verification of Space axioms:
V1. (V/W, +) is an abelian group.
In Group theory it has already been shown that (V/W, +) is an abelian group.
V2. Scalar multiplication is distributive over addition of coset: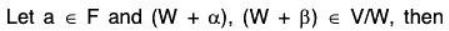
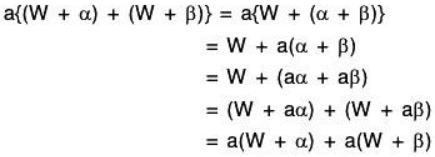
Therefore scalar multiplication is distributive over addition of cosets in V/W.
V3. Scalar addition is distributive over scalar multiplication: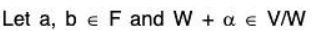
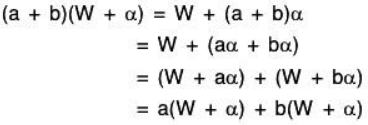
Therefore scalar addition is distributive over scalar multiplication in V/W.
V4. Associativity for scalar multiplication: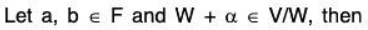
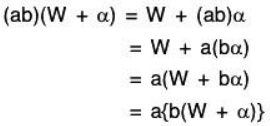
Therefore scalar multiplication is associative in V/W.
V5. Let 1 ∈ F, is the unit element of F, then for W + α ∈ V/W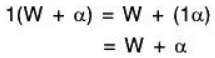 From the above discussion, it is clear that V/W satisfy all the space axioms. Hence V/W is a vector space over the field F.V/W is called the Quotient space or Factor space of V relative to W Dimension of a Quotient Space
From the above discussion, it is clear that V/W satisfy all the space axioms. Hence V/W is a vector space over the field F.V/W is called the Quotient space or Factor space of V relative to W Dimension of a Quotient Space
Theorem: If W be a subspace of a FDVS V(F), then:
dim(V/W) = dimV - dimW.
Proof. Let dim V = n and dim W = m. Clearly, m ≤ n.
Let 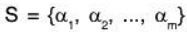 be the basis of W.Since S is a LI subset of V, therefore this can be extended to form the basis of V. Therefore let the extended set
be the basis of W.Since S is a LI subset of V, therefore this can be extended to form the basis of V. Therefore let the extended set 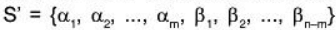 be the basis for V.
be the basis for V.
Now we will show that the set of (n - m) cosets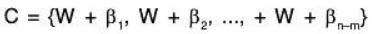 is a basis of V/W.C is LI: Let a1, a2...... an-m ∈ F such that
is a basis of V/W.C is LI: Let a1, a2...... an-m ∈ F such that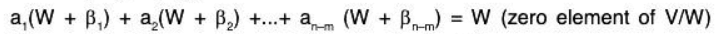
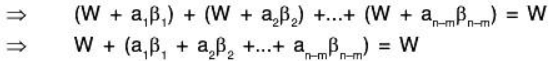
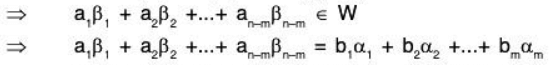
[since any element of W can be expressed as a LC of elements of its basis S]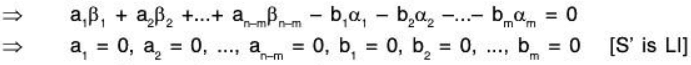
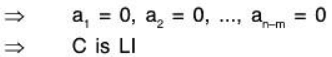
V/W = L(C): Let W + α be any element of V/W where α ∈ V but S’ is a basis of V, therefore α = LC of elements of S’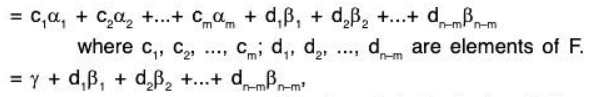
where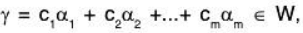
since S is the basis of W.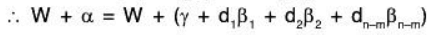
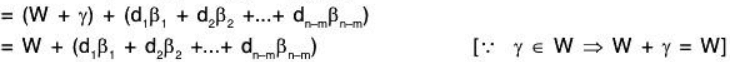
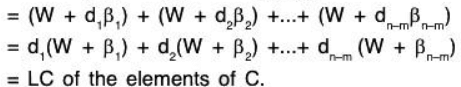 ⇒ V/W = L(C)∴ C is a basis of V/W.
⇒ V/W = L(C)∴ C is a basis of V/W.
⇒ dim(V/W) = n - m = dimV - dimW.
Co-ordinate Representation of a vector
With the help of the basis, we can determine the co-ordinates of any vector α ∈ V which is just similar to natural co-ordinates of α.
For example, if {e1, e2,..... en} is a standard (natural) basis of Vn(F) where e1 = (1, 0, 0......0), e2 = (0, 1, 0, .... 0), en = (0, 0, 0, ..... 1)
then any  can be expressed as LC of basis vectors i.e.
can be expressed as LC of basis vectors i.e.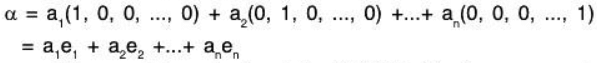
If 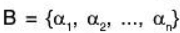 is an arbitrary basis of the FDVS Vn(F), then any vector α of Vn can be uniquely expressed as a LC of basis vectors α1, α2,..... αn.
is an arbitrary basis of the FDVS Vn(F), then any vector α of Vn can be uniquely expressed as a LC of basis vectors α1, α2,..... αn.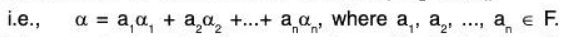
The n-tuple of scalars (a1, a2,..... an) used in this LC is called the co-ordinates of a relative to the basis B.
But in the basis B, the basis vectors can be written in any order. By changing the order of the vectors, the c-ordinates of α are changed.
Ordered Basis: If the vectors of B are kept in a particular form by a well defined way, then B is called the Ordered Basis for V. The co-ordinates of any vector of the space of unique wrt an ordered basis.
➤ Co-ordinates of a Vector.
Definition:
Let V (F ) be a FDVS. Let B = ( α1, α2,..... αn) be an ordered basis for V. Again in let α ∈ V, then ∃ a unique n-tuple (x1, x2, ..... ,xn) of scalars such that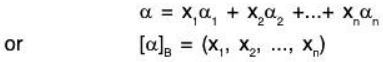
The n-tuple (x1, x2, ..... ,xn) is called n-tuple of co-ordinates of relative to the ordered basis B. The scalar xi is called ith co-ordinate of relative to the ordered basis B.
Example 1: Show that S = {(1, 1, 1), (0, 1, 1), (0, 0, 1)} is a basis for the space V3(ℝ). Also find the co-ordinates of α = (3, 1, -4) ∈ V3(ℝ) relative to this basis.
Clearly S ⊂ V3(ℝ).
S is LI: Let there exist a1, a2, a3 ∈ ℝ such that
Therefore the required co - ordinates are (3, - 2 , - 5)
Example 2: Find the co-ordinates of the vector (a, b, c) of V3(ℝ) relative to its basis S = {(1, 1, 1), (1, 1, 0), (1, 0, 0)}.
Let a1, a2, a3 ∈ ℝ
Therefore the required co-ordinates are (c, b - c, a - b).
Example 3: Find the co-ordinates of the vector p(x) = 2x2 - 5x + 6 of P2[x] of all polynomials over R with degree < 2, relative to its basis S = {1, x - 1, x2 - x + 1}
Let a1, a2, a3 ∈ R such that
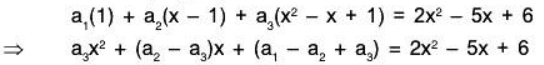
Therefore the required co -ordinates are (3, - 1 , 2).
Example 4: If V (R ) be the vector space over the real field of all 2*2 matrices and 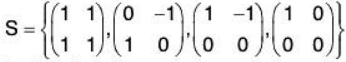 be a basis of it, then find the co-ordinates of
be a basis of it, then find the co-ordinates of 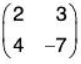 relative to the basis.
relative to the basis.
Let a1, a2, a3 ∈ R such that
Solving the equations,a, = -7, a2 = 11, a3 = -21, a, = 30
Therefore the required co-ordinates are (-7, 11, -21, 30).
Example 5: Let V3(ℝ) be a FDVS. Find the co-ordinate vector of = (3, 1, -4) relative to the following basis: v = (0, 0, 1); v2 = (0, 1, 1); v3 = (1, 1, 1)
Let a1, a2, a3 ∈ R such that
i.e. (3, 1, -4) = a1(0, 0, 1) + a2(0, 1, 1) + a3(1, 1, 1)
⇒ a3 = 3, a2 + a3 = 1, a1 + a2 + a3 = -4
⇒ a1 = -5, a2 = -2, a3 = 3
∴ The required co-ordinates of v wrt the given basis are [v] = (-5, -2, 3)
|
98 videos|34 docs|32 tests
|
FAQs on Vector Space & Linear Transformation- 2 - Mathematics for Competitive Exams
| 1. What is a linear combination? |  |
| 2. How can we determine if a set of vectors form a subspace? |  |
| 3. What is the difference between linear dependence and linear independence? |  |
| 4. What is a basis and dimension of a vector space? |  |
| 5. How are vector spaces and linear transformations related? |  |