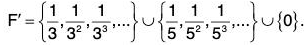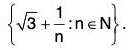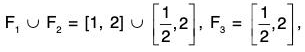Point Set Topology - II | Mathematics for Competitive Exams PDF Download
Neighbourhood of a Point
- Definition: A set S ⊂ R is called a neighbourhood (nbd) of a point p ∈ R if there exists an open interval (p - ε, p + ε) for some ε > 0,
such that p ∈ ( p - ε, p + ε) ⊂ S. - Properties
1. The set R of real numbers is nbd. of all its points.
For any real number x, we have x ∈ (x - ε x + ε) ⊂ R, ε > 0.
2. The open interval (a, b) is a nbd. of all its points, since
x ∈ (a + ε, b - ε) ⊂ (a,b)
3. The half open interval (a, b] is a nbd, of all its points except b, since for any ε > 0
b ∈ [b - ε, b + ε ) <z ( a, b]. (∵ b + ε > b)
Similarly, [a, b) is a nbd. of all its points except a and [a, b] is a nbd. of all its points except a and b.
4. The set Z of integers is not a nbd. of any of its points, since for any integer p and any ε > 0, p ∈ (p - ε , p + ε ) ⊄ Z.
5. Each of the following open intervals.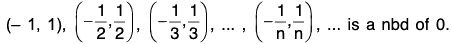
6. For any p ∈ R, N = {p} is not a a nbd. of p, since for any ε > 0, (p - ε , p + ε ) ⊂ N.
7. The set Q of rational numbers is not a nbd. of any of its points, for if (a, b) is any open interval around a point p ∈ Q, then p ∈ (a, b) ⊂ Z. Since between any two real numbers a, b there is always an irrational number which does not belong to Z.
8. The set R ~ Q of irrational numbers is not a nbd. of any of its points.
9. A non-empty finite set S is not a nbd. of any of its points, if (a, b) is any open interval around any point x ∈ S, then
x ∈ (a, b) ⊄ S,
since (a, b) necessarily contains infinite number of points and S is a finite set.
10. The empty set Ф is a nbd. of each of its points, since there is no point in Ф which is not a nbd. - Examples
Example 1: If M is a nbd. of a point p and N ⊃ M, then N is also a nbd. of the point p.
Since M is a nbd. of the point p therefore, there exists an open interval (p - ε, p + ε),
ε > 0 such that
p ∈ (p - ε, p + ε) ∈ M
⇒ P ∈ (p - ε, P + ε) ⊂ M ⊂ N [∵ N ⊃ M ⇒ M ⊂ N]
⇒ P ∈ (p - ε, p + ε) ⊂ N.
Hence N is a nbd. of p.
Example 2: If M and N are nbds. of a point p, then M ∩ N is also a nbd. of p.
Since M and N are nbds. of p, therefore, there exist ε1 > 0 and ε2 > 0 such that
p ∈ (p - ε1, + ε2) ⊂ M,
and p ∈ (ε2 - c2, p + ε2) ⊂ N.Let ε = min {ε1, ε2} so that ε < ε1, and ε < ε2. Thus
....(1)
∴ p ∈ (p - ε, p + ε) ⊂ M ∩ N.
Hence M ∩ N is a nbd of p.
Note. Obviously, p ∈ (p - ε, p + ε) ⊂ M υ N and so M υ N is also a nbd. of p.
Example 3: Show that the intersection of a finite number of neighbourhoods of a point is also a neighbourhood of the point.
Let M1, M2,Mn be a finite number of neighbourhoods of a point p. Then there exists εi > 0 such that
p ∈ ] p - εi, p + εi [ ⊂ Mi for i = 1, 2,...., n.
Let ε = min {ε1, ε2, .... εn. Then
p ∈ ] p - ε, p + ε [ ⊂ Mi for i = 1, 2, n
⇒ p ∈ ] p - ε, p + ε [ c M1, ∩ M2 ∩ ... ∩ Mn.
Hence M1 ∩ M2 ∩ ... ∩ Mn is a nbd. of p.
Example 4: Define a neighbourhood of a point. Show that the intersection of the family of all neighbourhoods of a point x is {x}.
A subset S ⊂ R is called a neighbourhood of a point p ∈ R if there exists some ε > 0 such that ( p - ε, p + ε ) ⊂ S,
Let {Nx} be a family of all neighbourhoods of a point x. We have to show that ∩ Nx = {x}.
Consider any point y ≠ x and Let ε = I x - y |
then, (x - ε, x + ε) is a nbd. of x and y ∉ (x - ε, x + ε),
since y ∈ (x - ε, x + ε) ⇒ x- ε < y < x + ε ⇒ lx-y| < ε, a contradiction.
Since y ∉ (x - ε, x + e), y ∉ n Nx. Hence n Nx = {x}.
Example 5: (i) Can a set N be a neighbourhood of any point of R ~ N?
(ii) Can a non-empty finite set be a neighbourhood of any of its points?
(i) We shall show that N cannot be a neighbourhood of any point of R ~ N.
Let x ∈ R ~ N then, x ∉ N.
Suppose N is a nbd. of x then there exists some c > 0 such that
x ∈ (x - ε, x + ε) ⊂ N ⇒ x ∉ N, which is a contradiction.Hence the assertion made above is not TRUE.
(ii) The answer of the second part is also No.
Let x ∈ N, where N is a non-empty finite set. If N is nbd. of x, then
x ∈ (x - ε, x + ε) ⊂ N for some ε > 0.This is impossible, since N is a finite set and (x - ε, x + ε) contains infinite number of elements.
Limit Points
- Definition 1 : A real number p is said to be a limit point of a set S ⊂ R if for each ε > 0 there exists at least one point p1 ∈ S such that
P1 ∈ (p - ε, p + ε) and p1 ≠ p. - Definition 2 : The set of all limit points of a set S ⊂ R is called the derived set of S and is denoted as S’.
x ∈ S' ⇔ x is a limit point of S. - Example
1. 0 is the only limit point of the set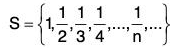 2. 1 and -1 are the only limit points of the set
2. 1 and -1 are the only limit points of the set Notice that 1, -1 both belong to S and S’ = {1, -1}.
Notice that 1, -1 both belong to S and S’ = {1, -1}.
Remarks
1. A set may or may not have a limit point.
For Example, R has limit points but Z has no limit point.
2. Limit point of a set may or may not belong to the set.
For Example, every limit point of R belongs to R and the only limit point 0 of the set does not belong to the set i.e., 0 ∉ S’.
does not belong to the set i.e., 0 ∉ S’.
2. The set I has no limit point for a nbd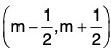 of m ∈ 1 contains no Point I other than m. Thus the derived set of I is the null set ∅.
of m ∈ 1 contains no Point I other than m. Thus the derived set of I is the null set ∅.
3. Every point of R is a limit point for every nbd of any of its points contains an infinity of members of R. Therefore, R’ = R.
Solved Examples
Example 1: Find the limit points of each of the following sets :
(a)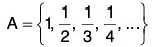 (b)
(b)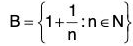 (c)
(c)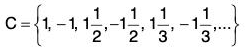 (d) D = {x : 0 < x < 1}
(d) D = {x : 0 < x < 1}
(e)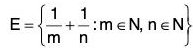 (f) F = {3-n + 5-n : n ∈ N}
(f) F = {3-n + 5-n : n ∈ N}
Sol:
(a) The only limit point of A is 0 i.e., A’ = {0}. Notice that 0 ∉ A.
(b) We have B =The only limit point of B is 1 i.e., B’ = {1}. Notice that 1 ∉ B.(c) The set C =
has only two limit points 1,-1. Notice that 1 e C and -1 e C. We have C' = {1, -1}.
(d) We observe that D = [0, 1) and so D' = [0, 1].
(e) First we write all the elements of the setFor m = 1, the elements of E are :
...(1)For m = 2, the elements of E are :
...(2)For m = 3, the elements of E are
...(3)and so on.It is clear that1 is the limit point of the elements in row (1),
1/2 s the limit point of the elements is row (2),
1/3 is the limit point of the elements in row (3),
and so on.
Thus... are all limit points of E.
Since E contains an infinite number of fractions lying between 0 and 1, so each nbd. of 0 surely contains a positive fraction and as such 0 is also a limit point of E.
Hence(f) We have
As discussed in part (e), we observe that
Example 2: Give an example of a set whose derived set is
(i) void
Ans. If Z is the set of integers, then Z' = Ф
(ii) subset of the given set
Ans. Let S =
Then S’ = { 1 , - 1 } ⊂ S.
(iii) superset of the given set
Ans. Let S =
Then S’ = {0}.S’ is neither a subset nor a superset of S.
(iv) same as the given set
Ans. R' = R or [a, b]’ = [a, b].
Example 3: Give an example of a set which has
(i) no limit point
Ans. The set Z of integers has no limit point.
(ii) unique limit point
Ans.
has 0 as the unique limit point.
(iii) two limit points
Ans.
has two limit points viz 1 and -1.
(iv) three limit points
Ans.
has three limit points viz. 1, 2, 3
(v) infinite number of limit points
Ans. The set R of real numbers has infinite number of limit points. In fact every real number is a limit point of R.
(vi) a set whose every point is a limit points of the set
Ans. The set R of real numbers.
(vii) a set none of whose points is a limit point of the set
Ans. The set Z of integers.
(viii) A set with only √3 as its limit point.
Ans. S =
Example 4: Define limit point of a set. Show that the set N of natural numbers has no limit point.
Let m be any natural number.
Thenis a nbd. of m which does not contain any point of N different from m.Let m ∈ R ~ N i.e., m is any real number but not a natural number. Then we can find some integer j such that j < m < j + 1. Consequently (j, j + 1) is a nbd. of m, which does not contain any point of N. Hence N has no limit point i.e., N' = Ф.
Example 5: Given an example each of :
(i) a bounded set of real numbers
(ii) an unbounded set of real numbers
Also find the set of limit points of both the sets.
(i)
is a bounded set of real numbers. Its limit points are 1 and -1.(ii)
is an unbounded set of real numbers. 0 is the only limit point of S.
Example 6: Find the derived sets of the following :
(i)  (ii)
(ii)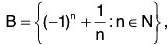 (iii)
(iii)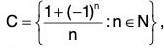 (iv)
(iv)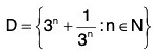
A’ = {1}, B’ = {-1, 1}, C’ = {0}, D’ = ϕ
Example 7: If S and T are sets of real numbers, then show that
(a) S ⊂ T ⇒ S’ ⊂ T’
(b) (S ∪ T)’ = S’ ∪ T’
(c) (S ∩ T)’ ⊂ S’ ∩ T’
Given an example to show that (S ∩ T)’ and S’ ∩ T’ may not be equal.
(a) Let S ⊂ T. We shall prove that S’ ⊂ T’.
Let x ∈ S’ so that x is a limit point of S. Thus for each ε > 0, (x - ε, x + ε) contains a point x, ∈ S such that x1 ≠ x. Since S ⊂ T, x1 ∈ S ⇒ x1 ∈ T.
Consequently, (x - ε, x + ε) contains a point x1 ∈ T, x1 ≠ x, and so x is a limit point of T
i.e., x ∈ T’.
∴ x ∈ S' ⇒ x ∈ T’.Hence S ’ ⊂ T
(b) We know S ⊂ S ∪ T S’ ⊂ (S ∪ T),, by part (a).Similarly, T ⊂ S ∪ T ⇒ T ’ ⊂ (S ∪ T)’.
S’ u T ' ⊂ (S ∪ T) ’ ...(1)
∴ Now we prove (S ∪ T)’ ⊂ S’ υ T’. ...(2)
Let x ∈ (S ∪ T)' ⇒ x is a limit point of S ∪ T
⇒ every nbd. of x contains a point y ∈ S ∪ T, y ≠ x
⇒ every nbd. of x contains a point (y ∈ S or y ∈ T), y ≠ x
⇒ every nbd. of x contains a point y ∈ S, y ≠ x,
or every nbd. of x contains a point y ∈ T, y ≠ x.
⇒ x is a limit point of S or x is a limit point of T
⇒ x ∈ S’ or x ∈ T’⇒ x ∈ S’ ∪ T'.
Thus (2) is proved.
From (1) and (2), (S ∪ T)' = S’ υ T.
(c) We know S ∩ T ⊂ S ⇒ (S ∩ T)' c S’, by part (a)
and S ∩ T ⊂ T ⇒ (S ∩ T)’ ⊂ T.
(S ∩ T)’ ≠ S’ ∩ T,.
To prove that the equality does not hold, we take
S = ]1, 2[ and T = ]2, 3[ so that S ∩ T = ϕ.
⇒ S’ = [1, 2], T = [2, 3] and
(S ∩ T)’ = ϕ' = ϕ).
Now S’ ∩ T' = {2} and (S ∩ T)’ = ϕ.
Thus (S ∩ T)' ≠ S’ ∩ T.
Some Theorems on Limit Points
Theorem 1 : A point p is a limit point of a set A if and only if every neighbourhood of p contains infinitely many points of A.
Proof. The condition is necessary.
Let p be a limit point of A. We shall show that every nbd. of p contains infinitely many points of A. Suppose this is false then, there exists some ε > 0 such that (p - c, p + e) contains only a finite number of points, say pt, p2, pn ; which are different from p.
Let δ = min {Ip - p1 I , I p - p2 I ,..., I p — pn I } (δ > 0)
⇒ δ < I p - Pi I for i = 1, 2 ..., n
⇒ (p - δ, p + δ) contains no point of A other than p
⇒ p is not a limit point of A, which is a contradiction.
Hence every nbd. of p must contain infinitely many points of A.
The condition is sufficient.
Suppose every nbd. of p contains infinitely many points of A. Surely then, every nbd. of p contains a point of A different from p and so p is a limit point of A.
Corollary. Show that a finite set has no limit points.
Proof. Let S be a finite set. Let if possible p be a limit point of S.
By Theorem for every ε > 0, (p - c, p + c) must contain an infinite number of elements of S, which is impossible, as S is a finite set. Hence p cannot be a limit point of S.
Theorem 2 : (Bolzano-Weierstrass Theorem): Every infinite bounded set of real numbers has a limit point.
Proof. Let S be any infinite bounded set of real numbers with bounds
m = inf S and M = sup S i.e., m < x < M ∀ x∈S. ...(1)
We define a set of real numbers as follows :
T = {x : x Exceeds only a finite number of elements of S}. ...(2)
From (2), it follows that
⇒ x g S’ u T'.
Thus (2) is proved.
From (1) and (2), (S ∪ T)' = S’ ∪ T'
(c) We know S ∩ T ⊂ S ⇒ (S ∩ T)' ⊂ S’, by part (a)
and S ∩ T ⊂ T ⇒ (S ∩ T)’ ⊂ T.
(S ∩ T)’ ⊂ S’ ∩ T,.
To prove that the equality does not hold, we take
S = ]1, 2[ and T = ]2, 3[ so that S ∩ T = ϕ.
⇒ S’ = [1, 2], T = [2, 3] and
(S ∩ T)’ = ϕ, = ϕ.
Now S’ ∩ T' = {2} and (S ∩ T)’ = ϕ.
Thus (S ∩ T)' ≠ S’ ∩ T.
(i) The set Z of integers is an infinite unbounded set, which has no limit point.
(ii) The set S = {12, 22, 32, ... n2, ...}
is an infinite unbounded set, which has no limit point.
Remark : It may, however, be noticed that
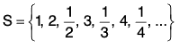
is an infinite unbounded set, which has the limit point viz. 0.
Theorem 3 : Every finite set is bounded.
Proof : Let A = {a1, a2, .... an} be a finite set and
let h = min(a1, a2, .... an) and k = max(a1, a2, ..., an)
then h < x < k, ∀ x ∈ A
Therefore A is bounded.
Theorem 4 : Every infinite bounded set of real numbers has a limit point.
Proof : Every infinite and bounded subset of R has a limit point i.e. atleast one limit point.
The Archimedean Property Of Real Numbers
Definition: If x, y are two positive real numbers, then there exists a positive integer n such that ny > x.
Proof: Suppose there does not exist any positive integer n such that ny > x. Then ny < x ∀ n ∈ N. Consequently, the set
S = {y, 2y, 3y ny, (n + 1) y, ...}
is non-empty and bounded above by x.
By order-completeness property, S has the supremum, say p.
∴ (n + 1) y < p ∀ n ∈ N
⇒ ny < p - y ∀ n ∈ N, (p - y < p, as y > 0)
⇒ p - y (< p) is an upper bound of S, which is a contradiction to the fact that p = sup S.
Corollary 1 : If x be any positive real number, then there exists a positive integer n such that n>x.
Corollary 2 : Let x by any real number and y be a positive real number, then there exists a positive integer n such that ny > x.
Corollary 3 : For any real number x, there exists a positive integer n such that n > x.
Corollary 4 : For any real number x, there exists an integer m such that m < x.
Example 1: If x be any positive real number, then there exists a positive integer n such that 1/x < x.
Applying the Archimedean property, for y = x > 0 and x = 1, there exists a positive integer n such that ny > x nx > 1 ⇒ n > 1/x. Hence 1/n < x.
Remark : The integer n satisfying n < x < n + 1 is called an integral part of x and is denoted by [x].
Example 2: If x and y are real numbers and x > 1, prove that there exists a positive n such that xn > y.
Suppose that conclusion of the problem is false.
Then xn < y ∀ n ∈ N. Consequently, the set
S = {x, x2, x3, ..., xn, ...}is non-empty subset of R, which is bounded above by y. By order-completeness property of R, S has the l.u.b. Let p = l.u.b. S. ...(1)
Since x > 1, px > p ⇒ p > p/x ⇒ p/x < p
⇒ p/x is not an upper bound of S, by (1) and so there exists some xn ∈ S such that
xn > p/x ⇒ xn +1 > p, where xn +1 ∈ S.Thus shows that p is not an upper bound of S, which is a contradiction.
Hence xn > y for some positive integer n.
Intervals
The representation of real numbers as points on a straight line helps us to define four types of intervals.
Let a and b be any two real numbers such that a < b.
1. Open Interval
- denoted by ]a, b[, is defined as
- (a, b) = {x : a < x < b}.
- The end points a and b do not belong to (a, b).
2. Closed Interval
- denoted by [a, b], is defined as
- [a, b] = {x : a < x < b}.
- The end points a and b belong to [a, b].
3. Semi-Open or Semi-Closed Intervals are defined as follows:
i. (a, b] = {x : a < x < b}.
- Here a ∉ (a, b] and b ∈ (a, b].
- The interval ]a, b] is said to be open from the left and closed from the right.
ii . [a, b) = {x : a < x < b}.
- Here a ∈ [a, b) and b ∉ [a, b).
- The interval [a, b) is said to be open from the right and closed from the left. The intervals (a, b] and [a, b) are also known as half-open or half-closed intervals.
Open And Closed Sets
Open Sets
- Definition: A set S ⊂ R is called an open set if it is a nbd of each of its points
- In Other Words : a set S ⊂ R is called an open set if for each p ∈ S, there exists some ε >0 such that p ∈ (p - ε, p + ε) ⊂ S ∀ p ∈ S.
- Properties
1. The set R of real numbers is an open set.
2. Every open interval (a, b) is an open set.
3. [a, b) is not an open set, since [a, b) is a nbd. of all is points except a. Similarly, (a, b], [a, b] are not open sets.
4. The set Z is integers is not an open set,
since Z is not a nbd. of each of its points.
5. G = (1, 2) ∪ (3, 4) is an open set, as G is a nbd. of each of its points.
6.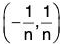 is an open set for each n e N.
is an open set for each n e N.
7. The empty set ϕ is an open set.
8. The singleton set {x} is not an open set, since for any ε > 0, (x - ε, x + ε) ⊄ {x}
9. The set Q of rational numbers is not an open set, since Q is not a nbd. of each of its points.
10. The set R - Q of all irrational numbers is not an open set.
11. The set S = is not an open set, as S is not a nbd. of each of its points.
For Example, (1 - ε, 1 + ε) is not an open set, as S is not a nbd. of each of its points.
For Example, (1 - ε, 1 + ε) contains an infinite number of irrational numbers and so (1 - e, 1 + ε) ⊂ S for each ε > 0.
 |
Download the notes
Point Set Topology - II
|
Download as PDF |
Theorems based on Open Sets
Theorem 1: The union of an arbitrary family of open sets is an open set.
Proof. Let {GI : λ ∈ A} be an arbitrary family of open set.
Let
. We have to show that G is an open set.
Let x be any element of G = ∪ Gλ
Then x ∈ Gλ for some X ∈ A.Since Gλ is given to be an open set and x ∈ Gλ so Gλ is a nbd. of x. Thus there exist some ε > 0 such that
x ∈ (x - ε, x + ε) ⊂ Gλ
⇒ x ∈ (x - ε, x + ε) ⊂ Gλ ⊂Gλ = G
⇒ x ∈ (x - ε, x + ε) ⊂ G ∀ x ∈ G
⇒ G is a nbd. of x, ∀ x ∈ GIt follows that G is a nbd. of each of its points and consequently G = Gλ. is an open set.
Theorem 2: The intersection of a finite number of open sets is an open set.
Proof. First of all we show that the intersection of two open sets G1 and G2 is an open set. Let x be any point of Gt n G2. Then x ∈ G1 ∩ G2
⇒ x ∈ G1 and x ∈ G2⇒ G1 and G2 are nbds. of x (∵ G1 and G2 are open sets)
⇒ G1 ∩ G2 is nbd. of x
⇒ G1 ∩ G2 is a nbd. of x for each x ∈ G1 ∈ G2.
Thus G1 ∩ G2 is an open set.
Now we consider three open sets G1,G2, G3. Then
G1 ∩ G2 n G3 = (G1 ∩ G2) ∩ G3.R.H.S. being the intersection of two open sets viz. G1 ∩ G2 and G3 is an open set and so G1 ∩ G2 ∩....∩ G3 is an open set.
Proceeding in a similar way, if G1, G2......, Gn are a finite number of open sets, then Gt n G2 ∩ ... ∩ Gn is an open set.
Remark : The intersection of an arbitrary family of open sets may not be an open set.
Let us consider Gn = ( - 1/n, 1/n ) ∀ n ∈ N. Then
G1 = ( - 1, 1), G2 = (- 1/2, 1/2 ), G3 = (- 1/3, 1/3), ...
Since every open interval is an open set, therefore {Gn : n ∈ N} is a family of infinite number of open sets.
Clearly, G1 ∩ G2 = (- 1, 1) ∩ (- 1/2, 1/2) = (- 1/2, 1/2),
G1 ∩ G2 ∩ G3 = (- 1/2, 1/2) ∩ ( - 1/3, 1/3) = (- 1/3, 1/3)
and so on. Thus at every step, the size of the open interval is reducing and getting closer to 0.
IndeedGn = {0} which is not an open set,
}since for any ε > 0, (0 - ε, 0 + ε) = (- ε, ε) ⊄ {0}.
Closed Sets
- A closed set in a topological space is a set whose complement is open.
- Properties
1. The set R of real numbers is a closed set,
as R ~ R = ϕ is an open set.
2. The empty set ϕ is a closed set,
as R ~ ϕ = R is open set.
3. The set R of real numbers is both open and closed.
The empty set ϕ is both open and closed.
4. Every closed interval [a, b] is a closed set,
∵ R ~ [a, b] = (- ∞, a) ∪ (b, + ∞)
and R.H.S. being the union of two open sets is an open set.
5. [a, b) is not a closed set,
R ~ [a, b) = ( - ∞, a) ∪ [b, + ∞) is not an open set as the R.H.S. is a nbd. of each of its points except b.
Similarly, (a, b], (a, b) are not closed sets.
6. [0, 3] ∩ [1, 2] is a closed set,
since [0, 3] ∩ [1, 2] = [1, 2], which is a closed set.
7. F = [1, 2] ∪ [2, 4] is a closed set, since F = [1, 4] is a closed set.
8. Q is not a closed set, since R ~ Q being the set of all irrational numbers is not an open set. Thus the set Q of rational numbers is neither a closed set nor an open set. - Examples
Example 1 : Let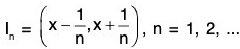
Prove that ln is an open set for each positive integer n and
Sol: Since each open interval is an open set, (x - 1/n, x + 1/n) is an open set for n = 1, 2, 3,
... As shown above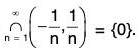 Similarly,
Similarly,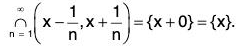
Example 2: Is every infinite set open? Justify your answer.
Ans: Every infinite set need not be an open set.
Remarks:
(i) the set Z of integers is an infinite set, which is not an open set.
(ii)is an infinite set, which is not an open set.Definition : A set S ⊂ R is called a closed set if and only if its complement R ~ S is an open set.
S is closed ⇔ R ~ S is open.
Theorems Based on Closed Sets
Theorem 1: (a) The union of a finite number of closed set is a closed set.
(b) The intersection of an arbitrary family of closed sets is a closed set.
(c) Given an Example to show that an arbitrary union of closed sets may not be a closed set.
Proof:
(a) Let F1, F2, ..., Fn be a finite number of closed sets so that R ~ F1, R ~ F2, ..., R ~ Fn are open sets.(R ~ F1) n (R ~ F2) ∩ ... ∩ (R ~ Fn) is an open set.
By De Morgan’s law,
R~(F1u F2 ∪ ... ∪ Fn) = (R ~ F1) n (R ~ F2) ∩ ... ∩ (R ~ Fn)
⇒ R ~ (F1 ∪ F2 ∪ ... ∪ Fn) is an open set.
Hence F1 u F2 ∪ ... ∪ Fn a closed set.
(b) Let {Fλ : X ∈ ∧} be an arbitrary family of closed sets.
We have to prove that
is a closed set.
Equivalently, we have to prove that R ~ F is an open set.
By De Morgan's law,
R ~ F = R ~ (∩ Fλ) = ∪ (R ~ Fλ).
Since each Fλ is a closed set, so R ~ Fλ is an open set.
Now ∪ (R ~ Fλ) being an arbitrary union of open sets is an open set and so R ~ F is an open set. Hence F = ∩ Fλ is a closed set.
(c)Then
Since every closed interval is a closed set, therefore {Fn : n ∈ N} is a family of infinite number of closed sets. We observe that
Indeed,
which is not a closed set.
Theorem 2 : A set S is closed if and only if it contains all its limit points.
Equivalently, S is closed o S' ⊂ S.
Proof : By definition of a closed set,
S is closed ⇔ R ~ S is an open set
⇔ R ~ S is a nbd. of each of its points
⇔ for each x ∈ R ~ S, ∃ some c > 0, such that
(x - ε, x + ε) ⊂ R ~ S or (x - ε, x + ε) ∩ S = ϕ(∵ y ∈ (x - ε, x + ε) ⇒ y ∈ R ~ S ⇒ y ∉ S)
⇔ for each x ∈ R ~ S, ∃ a nbd. of x which contains no point of S
⇔ x is not a limit point of S ∀ x ∈ R ~ S.
⇔ x ∉ S’ ∀ x ∈ R ~ S
⇔ x ∉ S' ∀ x ∉ S
⇔ S' ⊂ S.
Remark. The above Theorem gives us a second definition of a closed set.
In order to show that a set S is closed, we must prove that if p is any limit point of S. then p ∈ S.
Corollary 1. Every finite set S is a closed set.
Proof. Since S is a finite set, S has not limit points. .\ S’ = ϕ.
Since ϕ ⊂ S. so S’ ⊂ S. Hence S is a closed set.
Corollary 2. Every singleton is a closed set.
Proof. Any singleton set {x} is a finite set and hence by Corollary 1, it is a closed set.
Corollary 3. The set Z of integers is a closed set.
Proof. We know Z‘ = ϕ and so Z’ ⊂ Z. Hence Z must be a closed set.
Corollary 4. The set N of natural numbers is a closed set.
Proof. We know N' = ϕ and so N' ⊂ N. Hence N is a closed set.
Theorem 3: Prove that the supremum of a non-empty bounded set is either the greatest member of the set or is a limit point of the set.
Or
Prove that the supremum of a non-empty bounded set S of real numbers when not a member of S must be a limit point of S.
Proof. Since S is non-empty and bounded above, S must have the supremum, say s i.e., s = sup S (O-C Property).
⇒ x < s ∀ x ∈ S.
If s < S, then s is the greatest member of S. Let s ∉ S.
We shall show that s is a limit point of S.
For any ε > 0, we have s - ε < s. ...(1)
Since s is the l.u.b. of S, so s - ε cannot be an upper bound of S. Consequently, there exists some t ∈ S such that
t < s < s + ε ⇒ t < s + ε. ...(2)
From (1) and (2), it follows that any nbd. (s - ε, s + ε) of s contains a point t ∈ S, t ≠ s. Hence s is a limit point of S.
Theorem 4 : Show that a non-empty, bounded and closed set S contains its supremum and infimum.
Proof : Since S is non-empty and bounded above S must have a supremum say s
i.e., s = sup S (O-C property). If we show that s ∈ S, then S has a maximum viz. s. We now proceed to show that s is a limit point of S.
Let ε > 0 be arbitrary. Since s = l.u.b.S. s - ε is not an upper bound of S and so there exists some t ∈ S such that
t > s - ε or s - ε < t ...(1)
Clearly, t < s < s + ε ...(2)
From (1) and (2), it follows that (s - ε, s + ε) contains a point t ∈ S, t ≠ s for all ε > 0.
Thus s is a limit point of S. Since S is a closed set, s ∈ S.
Hence s is a maximum of S. Similarly, s’ = inf S is a minimum of S.
Theorem 5 : Prove that the derived set of any set is a closed set.
Proof : Let S’ be the derived set of a set S. We have to show that S’ is a closed set. Equivalently, we have to show that if p is limit point of S’, then p ⇐ S’.
Suppose p is a limit point of S’. The for any ε > 0, (p - ε, p + ε) contains a point q of S’, q ≠ p. Now q ∈ S’ ⇒ q is a limit point of S.
⇒ Every nbd. of q (in particular, (p - ε, p + ε) ) contains a point r of S, r ≠ q
(∵ r ≠ q and q ≠ p)⇒ for each ε > 0, (p - ε, p + ε) contains a point r e S, where r ≠ p
⇒ p is a limit point os S p ∈ S’. Hence S’ is closed set.
Theorem 6 : The derived set of a bounded set is bounded.
Proof : Let S be any bounded set whose bounds are
m = inf S and M = sup Si.e., m < x < M ∀ x ∈ S ...(1)
We shall prove that
m < x < M ∀ x ∈ S’
Let, if possible, there exist some y ∈ S' such that y > M.
Now, y > M ⇒ y - M > 0.
We choose ε > 0 such that
ε < y - M ⇒ M < y - ε ...(2)
From (1) and (2),
x < x ∀ x ∈ S.
In follows that there exists a nbd. ( y - ε, y + ε ) of y which does not contain any point of S and so y in not a limit point of S i.e., y ∉ S’, which is contradiction.
Thus x < M ∀ x ∈ S’.
Similarly, we can show that
m < x ∀ x ∈ S’
Hence m < x < M ∀ x ∈ S' and so S’ is bounded.
Theorem7: Show that S =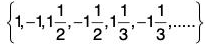 is closed but not open.
is closed but not open.
Proof:The only limit points of the set S are 1 and - 1 i.e., S’ = {1, - 1}.
Since S' ⊂ S, S is a closed set.Since S is not a nbd. of each of its points, S is not an open set.
Notice the for each ε > 0, 1 ∈ (1 - ε, 1 + ε) ⊄ S.
Solved Examples
Example 1: Given an example of each of the following :
(a) an interval which is an open set.,
Ans. (a, b)
(b) an interval which is not an open set,
Ans. [a, b]
(c) an open set which is not an interval,
Ans. R or (0, 1)U(2, 3).
(d) a set which is neither an interval nor an open set.
Ans. The set Z of integers.
Example 2: Give an example of each of the following :
(a) an interval which is a closed set,
Ans. [a, b].
(b) an interval which is not a closed set,
Ans. [a, b).
(c) a closed set which is not an interval,
Ans. R or [0, 1]U [2, 3].
(d) a set which is neither an interval nor a closed set.
Ans. The set Z of integers.
(e) A set which is neither an open set nor a closed set.
Ans. The set Q of all rational numbers is neither an open set nor a closed set. Example : Comment on the following statements :
(f) Can a finite set be open?
Ans. Yes. An empty set is a finite set, which is also an open set.
(g) Can a finite non-empty set be open?
Ans. No, Let S is a non-empty finite open set, then for any x ∈ S and any ε > 0
(x - ε, x + ε) ⊄ S,
since the interval (x - ε, x + ε) necessarily contains an infinite number of points and S is a finite set.
(h) Is every infinite set open?
Ans. No. The set Z of integers is an infinite set, which is not an open set.
(i) Is the intersection of any arbitrary family of open sets an open set?
Ans. No. Gn = ( - 1/n, 1/n) ∀ n ∈ N is a family of infinite number of open sets and
which is not an open set,
Example 3: Comment on the following statements :
(a) Can a singleton be closed?
Ans. Yes. Every singleton is closed
(b) Can a finite set be closed?
Ans. Yes. Every finite set is closed
(c) Is every finite set closed?
Ans. Yes.
(d) Is every infinite set closed?
Ans. No. S =
is an infinite set which is not closed, since its only limit point 0 does not belong to the set S
(e) Is the union of an arbitrary family of closed sets a closed set?
Ans. No. {Fn = [1/n, 2] : n ∈ N} is a family of infinite number of closed sets, and which is not a closed set.
(f) Is the intersection of an arbitrary family of closed sets a closed set?
Ans. Yes.
Example 4: Give Examples of sets S and S’ such that
(a) S ∩ S ’ = ϕ, ( b ) S ⊂ S ’ , (c) S ’ ⊂ S, (d) S = S ’ .
(a) Let S =
Then S’ = {0}. Clearly, S ∩ S’ = ϕ(b) Let S = ( 0, 1 ) so that S’ = [0, 1]. Obviously, S ⊂ S’.(c) Let S =
Then S’ = {1, - 1} c S.(d) Let S = [0,1] so that S’ = [0,1]. We have S = S’.
Example 5: Find the limit points of the following :
(i) N, (ii) (a, b], (iii) R ~ Q, (iv) finite set.
(i) N has no limit point.
(ii) {(a, b]}’ = [a,b]. Hence each point of [a, b] is a limit point of (a, b].
(iii) R ~ Q, consists of all irrational numbers. Every real number p ∈ R is a limit point of R ~ Q, since for each ε > 0, (p - ε, p + ε) contains an irrational number other than p.
(iv) A finite set has no limit point .
Example 6 : State whether the following subsets of R are open, closed :
(i) the set Z of all integers.
Ans. Z is closed, (∵ Z = ϕ ⊂ Z.)
However, Z is not open as Z is not a nbd. of any of its points.
(ii)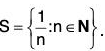
Ans. S is neither closed nor open.
We have S’ = {0} ⊄ S. Also S is not a nbd. of any of its points.
(iii) The segment (a, b).
Ans. It is an open set, since it is an open interval.
However, it is not a closed set, since { (a, b) }' = [a, b] ⊄ (a, b).
(iv) The set N of natural numbers.
Ans. N is closed. (v N’ = ϕ ⊂ N)
However, N is not open as N is not a nbd. of any of its points.
(v) S ={1, 2, 3, 4}.
Ans. S is a closed set, since it is a finite set and every finite set is closed. However, S is not open, since S is not a nbd. of any of its points.
(vi) The set R of real numbers.
Ans. R is both open and closed.
(vii) S = (0, 1) u (2, 3).
Ans. S being the union of two open sets is an open set.
Now S’ = { (0, 1) }’ u { (2, 3) }’ = [0, 1] u [2, 3] cz S.
Hence. S is not a closed set.
(viii)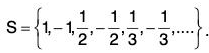
Ans. S’ = {0} ⊄ S and so S is not closed.Since S is not a nbd. of each of its points, S is not open.
(ix) The set Q as rational numbers.
Ans. We know Q’ = R ⊄ Q and so Q is not closed.
Further Q is not a nbd. of any of its points and so Q is not open.
(x) S = [0, 1] ∪ [2, 3].
Ans. S being the union of two closed sets is a closed set (Every closed interval is a closed set). Since S is not a nbd. of the points 0, 1,2, and 3, S is not an open set.
Example 7: It F is a closed bounded set, then every infinite subset S of F has limit point in F.
Ans: Since S is a subset of the bounded set F, so S is a bounded and infinite set. By Bolzano Weierstrass Theorem, S has a limit point, say p. Since S ⊂ F, so p is also a limit point of F. Since F is a closed set and p is a limit point of F, so p ⇐ F. Hence S has its limit point in F.
Example 8: If A is open and B is closed, show that A ~ B is open and B ~ A is closed.
Ans: Since B is closed, R ∼ B is an open set. Now A ~ B = A ∩ (R ~ B), which being the intersection of two open sets is an open set. Thus A ~ B is an open set.
Again B ~ A = B ∩ (R~A), which being the intersection of two closed sets is a closed set. Thus B ~ A is a closed set.
|
98 videos|28 docs|30 tests
|
FAQs on Point Set Topology - II - Mathematics for Competitive Exams
| 1. What are limit points in topology? |  |
| 2. How are closed sets defined in point set topology? |  |
| 3. What is the relationship between limit points and closed sets? |  |
| 4. Can a limit point belong to a set that is not closed? |  |
| 5. What are some important theorems related to closed sets and limit points? |  |