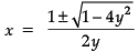Relations and Functions: Assertions & Reason Type Questions | Mathematics (Maths) Class 12 - JEE PDF Download
Question 1: Assertion (A) The relation R on the set N×N , defined by (a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N is an equivalence relation.
Reason (R) Any relation R is an equivalence relation, if it is reflexive, symmetric and transitive.
Options~
(a) Both A and R are correct; R is the correct explanation of A.
(b) Both A and R are correct; R is not the correct explanation of A.
(c) A is correct; R is incorrect.
(d) R is correct; A is incorrect.
Correct Answer is Option (a)
A relation between two sets is a collection of ordered pairs containing one object from each set. If the object x is from the first set and the object y is from the second set, then the objects are said to be related if the ordered pair (x, y) is in the relation.
A relation R is reflexive if each element is related itself, i.e. (a, a) ∈ R, where a is an element of the domain.
A relation R is symmetric in case if any one element is related to any other element, then the second element is related to the first, i.e. if (x, y) ∈ R then (y, x) ∈ R, where x and y are the elements of domain and range respectively.
A relation R is transitive in case if any one element is related to a second and that second element is related to a third, then the first element is related to the third, i.e. if (x, y) ∈ R and (y, z) ∈ R then (x, z) ∈ R.
Here, the given relation is:
(a, b) R (c, d) ⇔ a+d = b+c
Since, we know that (a +d)= (a + d).
Therefore, (a+d, a+d) ∈ R.
So, R is reflexive.
Now, suppose that (a + d, b + c) ∈ R.
Then we can write:
a+d=b+c
Or, b+c = a+d
So, (b+c, a+d) ∈ R.
This means that R is symmetric.
Now, let us take an ordered pair (a + d, b + c) ∈ R and (b + c, e+f) ∈ R.
We can write:
a+d=b+c..........(1)
And, b+c=e+f.............(2)
From equations (1) and (2), we can say that a+d = e+f.
So, (a + d, e + f) ∈ R.
This implies that R is transitive.
So, R is reflexive, symmetric as well as transitive.
We know that a relation which is symmetric, reflexive as well as transitive is an equivalence relation.
Therefore, the assertion is correct and reason is the correct explanation.
Hence, option (a) is the correct answer.
Question 2: Assertion (A) : f(x) = 1+x2 is a one to one faction from R+ → R,
Reason (R) : Every strictly monotonic function is a one to one function.
(a) Both A and R are true and R is the correct explanation of A,
(b) Both A and R are true but R is not the correct explanation of A,
(c) A is true but R is false,
(d) A is false but R is true.
Correct Answer is Option (a)
A monotonic function is a function between ordered sets that preserves or reverses the given order.
Given, f(x)=1+x2, domain is R+ and range is R
Now, for one to one function, we know, if f(x)=f(y) then x=y
∴ 1 + x21 = 1 + x22
⇒ x21 = x22 1 is cancelled in both sides
Thus, no negative value is considered.
A strictly monotonic function is either entirely non-increasing or non-decreasing, i.e., every element in the range maps to only one element in the domain.
∴ f(x) is strictly monotonic function and one-one function.
The correct option is (A)
Question 3: Assertion: The relation R given by R = {(1,3),(4,2),(2,4),(2,3),(3,1)} on a set A={1,2,3,4} is not symmetric.
Reason: For symmetric relation R = R−1.
(a) Both Assertion and Reason are correct and Reason is the correct explanation for Assertion
(b) Both Assertion and Reason are correct but Reason is not the correct explanation for Assertion
(c) Assertion is correct but Reason is incorrect
(d) Both Assertion and Reason are incorrect
Correct Answer is Option (a)
Both Assertion and Reason are correct and Reason is the correct explanation for Assertion.
R = {(1, 3),(4, 2),(2, 4)(2, 3)(3, 1)} as (2, 3) ∈ R but (3, 2) ∉ R
⇒ is not symmetric.
Question 4: The function f : R → R is defined by f(x) = cos2x + sin4x for x ∈ R. Then the range of f(x)is
(a) (3/4, 1]|
(b) [3/4, 1)|
(c) [3/4, 1]|
(d) (3/4, 1)|
Correct Answer is Option (c)
y = f(x) = cos2x + sin4x = cos2x + sin2x(1 − cos2x) = cos2x + sin2x − sin2xcos2x) = 1 − sin2xcos2x = 1 −(1/4)sin22x |∴ 3/4 ≤ f(x) ≤ 1| (∴ 0 ≤ sin22x ≤ 1)| ∴ f(x) ∈ [3/4,1]|
Question 5: Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Let W be the set of words in the English dictionary.
A relation R is defined on W as
R = {(x, y) ∈ W × W such that x and y have at least one letter in common}.
Assertion (A): R is reflexive. Reason (R): R is symmetric.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is True
Correct Answer is Option (b)
For any word x ∈ W
x and x have atleast one (all) letter in common
∴ (x, x) ∈ R, ∀ x ∈ W
∴ R is reflexive
Symmetric: Let (x, y) ∈ R, x, y ∈ W
⇒ x and y have atleast one letter in common
⇒ y and x have atleast one letter in common
⇒ (y, x) ∈ R ∴ R is symmetric
Hence A is true, R is true; R is not a correct explanation for A.
Question 6: Let R be the relation in the set of integers Z given by R = {(a, b) : 2 divides a – b}.
Assertion (A): R is a reflexive relation.
Reason (R): A relation is said to be reflexive if xRx, ∀x ∈ Z.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is True
Correct Answer is Option (a)
By definition, a relation in Z is said to be reflexive if xRx, ∀ x ∈ Z. So R is true.
a – a = 0 ⇒ 2 divides a – a ⇒ aRa.
Hence R is reflexive and A is true.
R is the correct explanation for A.
Question 7: Consider the set A = {1, 3, 5}.
Assertion (A): The number of reflexive relations on set A is 29.
Reason (R): A relation is said to be reflexive if xRx, ∀x ∈ A.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is True
Correct Answer is Option (d)
By definition, a relation in A is said to be reflexive if xRx, ∀ x ∈ A. So R is true.
The number of reflexive relations on a set containing n elements is 2n2 – n.Here n = 3.
The number of reflexive relations on a set A = 29–3 = 26.
Hence A is false.
Question 8: Consider the function f : R → R defined as f(x) = x3
Assertion (A): f(x) is a one-one function.
Reason (R): f(x) is a one-one function if co-domain = range.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is True
Correct Answer is Option (c)
f(x) is a one-one function if
f(x1) = f(x2) ⇒ x1 = x2.
Hence R is false.
Let f(x1) = f(x2) for some x1, x2 ∈ R
⇒ (x1)3 = (x2)3
⇒ x1 = x2
Hence f(x) is one-one.
Hence A is true.
Question 9: If A = {1, 2, 3}, B = {4, 5, 6, 7} and f = {(1, 4), (2, 5), (3, 6)} is a function from A to B.
Assertion (A): f(x) is a one-one function.
Reason (R): f(x) is an onto function.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is True
Correct Answer is Option (c)
Given, A= {1, 2, 3}, B = {4, 5, 6, 7} and f : A → B is defined as f = {(1, 4), (2, 5), (3, 6)} i.e., f(1) = 4, f(2) = 5 and f(3) = 6.
It can be seen that the images of distinct elements of A under f are distinct. So, f is one-one.
So, A is true.
Range of f = {4, 5, 6}.
Co-domain = {4, 5, 6, 7}.
Since co-domain ≠ range, f(x) is not an onto function. Hence R is false.
Question 10: Consider the function f : R → R defined as 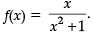
Assertion (A): f(x) is not one-one.
Reason (R): f(x) is not onto.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is True
Correct Answer is Option (b)
Given, f : R → R;
f(x) = x/(1+x2)
Taking x1 = 4, x2 = (1/4) ∈ R
f(x1) = f(4) = 4/17
f(x2) = f(1/4) = (4/17) (x1 ≠ x2)
∴ f is not one-one.
A is true.
Let y ∈ R (co-domain)
f(x) = y
⇒ (x/(1 + x2)) = y
⇒ y.(1 + x2) = x
⇒ yx2 + y – x = 0
⇒
since, x ∈ R,
∴ 1 – 4y2 ≥ 0
⇒ -(1/2) ≤ y ≤ (1/2)
So Range (f ) ∈ [-(1/2), (1/2)]
Range (f) ≠ R (Co-domain)
∴ f is not onto.
R is true.
R is not the correct explanation for A.
|
203 videos|307 docs|139 tests
|
FAQs on Relations and Functions: Assertions & Reason Type Questions - Mathematics (Maths) Class 12 - JEE
| 1. What is the difference between a relation and a function? |  |
| 2. How can we determine if a relation is a function? |  |
| 3. What is the difference between the domain and the codomain of a function? |  |
| 4. Can a function have the same input value but different output values? |  |
| 5. How can we determine if a function is one-to-one or onto? |  |