Overview: Two-Part Analysis | Data Insights for GMAT PDF Download
| Table of contents |

|
| What is Two-Part Analysis in GMAT? |

|
| Types of GMAT Two-part Analysis Questions |

|
| GMAT Two-Part Analysis Preparation Tips |

|
| GMAT Two-Part Analysis Questions and Explanations |

|
What is Two-Part Analysis in GMAT?
- Two-part analysis GMAT questions begin with a quant or verbal question. It then proceeds to a passage which is followed by a table having three columns.
- Each column will consist of five or six answer options. Each of them is again followed by two selection choices presented in an adverse manner in the second/third column.
- Two-part analysis GMAT tests the candidates on both quantitative and verbal concepts. It may examine GMAT quant concepts like two-dimensional Geometry, or probability, or powers and roots.
- It may also examine GMAT verbal concepts like weakening or strengthening arguments, inference-related questions, fact or assumptions, cause/effect relation. When candidates will practice GMAT two-part analysis questions, they will notice that the prompts are fixed, and there are no sorting options.
- It is to be remembered that candidates need to answer both the parts of the GMAT two-part analysis questions as there is no partial credit offered.
A candidate will be given two columns and the candidates need to correspond with each of the two columns to answer the question. Some two-part combinations include:
- Yes/No
- True/False
- Assumption/Conclusion
- Positive/Negative
- Prime/Non-Prime
Along with these, there can be any other kind of custom combination as well. The question comes with 6 options and you need to select two options from them. The answer choices are interrelated.
Types of GMAT Two-part Analysis Questions
There are three kinds of GMAT two-part analysis questions that candidates will come across.
- Verbal-based GMAT Two-Part analysis: To solve this question type, candidates will be required to use GMAT critical reasoning concepts like weakening/strengthening the arguments, looking for correlation or connections in the argument, and more.
- Quant-based GMAT Two-Part analysis: This is similar to solving quant questions where formulas and numbers will be present. The time taken to solve GMAT two-part analysis questions will be more as two questions are to be solved. They generally contain one part of problem-solving or GMAT data sufficiency questions which make them tricky.
- Logic-based GMAT Two-Part analysis: In this question type, candidates will work on scenarios. They will have a table or some other information to offer a parameter or constraint to the scenario.
GMAT Two-Part Analysis Preparation Tips
GMAT Two-part analysis questions need both critical reasoning and analytical skills to answer. The tips mentioned below can help the test-takers to solve the GMAT Two-part analysis questions correctly and within time.
- Question Scanning
Candidates need to start by scanning the question to understand its type. If there are formulas and numbers present, that is a quantitative question. If the question contains inferences, finding correlations, or assumptions then it is a verbal question. - Summarizing Information
After understanding the question type, proceed by summarizing the information given in the question. This is applicable for both verbal and quant-based questions. In case of rules questions, summarize all the rules given in the passage. - Determine if the task is dependent or independent
Candidates will be required to practice GMAT IR two-part analysis questions to know if the question is independent or dependent. They need to examine if the value of one answer is dependent on the other. In case the task is dependent, then follow an approach that relates both the answers. In the case of the independent task, solve the easier ones first. - Take Notes
The information in the passage can be quantitative and verbal data and sometimes, the combination of both. You may need to take notes to find out the answer. - Practice Table interpretations
Learn how to interpret the table and how to understand its relationship with the question. It may take time but it is possible. In GMAT two-part analysis, the answer has to be given in the form of a table, so it is necessary to learn. You can take the help of the books to understand table analysis and interpretation correctly. - Have Clarity
Understand what the question is actually asking. Try not to have any confusion regarding the question. It will be a great help in reaching the correct option.
Remember, until you understand exactly what is being asked, it will be twice difficult to answer. - Keep Common Sense Aside and Derive the answer from the provided Information
To solve the question, use your analytical knowledge to get the answer from the information provided. You don’t need to check whether the information is true or false. Also, you don’t need to check if anything is missing there.
Always stick to the information provided within the data. Remember, the answer has to be logically derived from the provided information – not from outside information. - Be Careful While Marking the Answer
Always review all the options before marking. Sometimes eliminating the wrong option leads us to the right answer quickly. But, before eliminating the answer option, be sure that it is the wrong one. The answer options are close and confusing – so, be extra careful. This saves time and helps in increasing speed too. - Go Through Realistic Question Papers
Over the internet, you can find out the GMAT practice papers for integrated reasoning. Go through these and practice every day to speed up. You are allowed to spend 2.5 minutes in each question but while solving the paper, you will feel that this time is not sufficient at all. As you master the skills, you will start to solve each question in less time.
GMAT Two-Part Analysis Questions and Explanations
Question 1:
Set 1: Red, Blue, Yellow
Set 2: Pink, Turquoise, Orange
Set 3: Purple, Green, Brown
Set 4: Black, White, Silver
A certain company is launching three new products. Color schemes for the packaging are to be selected from colors in the four sets above. Four different colors are needed for each product. For each color scheme, not more than two colors can be selected from one set, and colors from not more than three sets can be used.
The first three colors selected for each of the products are

Select a color that could be used for the fourth color for all three products. Select a color that could not be used as the fourth color for any of the products.
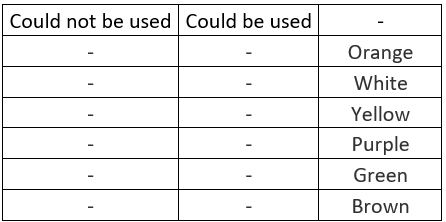
Solution: Since for product 1, the color cannot be purple, green or brown, or yellow, for product 2 it cannot be yellow or white as it is already used white and for product 3, it cannot be red, blue, or yellow. So, the fourth color for all the three products is Orange. After analyzing all these statements, it is clear that the color, which is not suitable to complete any of the color schemes, is Yellow.
Question 2: A taxi service charges a base fare of $5 and a rate of $M per mile for the first 10 miles. Thereafter the rate is $0.5M per mile. There is also a charge of $3 per suitcase. Students traveling from and to the local college get a twenty percent discount on the mileage rates. A is a teacher traveling a distance of 8 miles with one suitcase. B is a student traveling 30 miles with two suitcases from the college to the station.
Select the expression for the difference between the amounts paid by A and B in dollars, and for the amount paid by A in dollars.
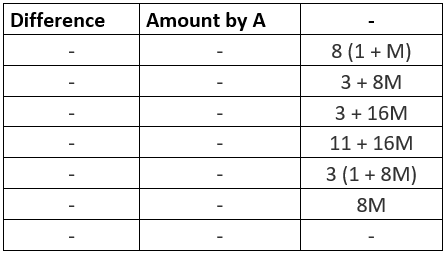
Solution: A has to pay 5+8M+3 which is equivalent to 8+8M which can also be written as 8(1+M). Also, B has to pay 5+0.8(10M+0.5M*20) which is equivalent to 11+0.8(20M) or it can be written as 11+16M.
The difference in their amount is 11+16M / 8+8M which is equivalent to 11+16M / 8-8M = 3+8M.
Question 3: On planet K, there is essentially no atmosphere, so objects in freefall experience no air friction. At time t = 0, an object released from rest accelerates downward at a uniform rate: it’s downward speed uniformly increases. At time t = 2 seconds, the object has fallen a distance D in meters from its original height. At time t = 5 seconds, the object is 75 meters below its original height and is moving at a downward speed of v in meters per second.
The table below, select values of D, the distance below the initial height at t = 2 seconds, and v, the downward speed at t = 5 seconds, that are consistent with the information provided. Make only two selections, one in each column.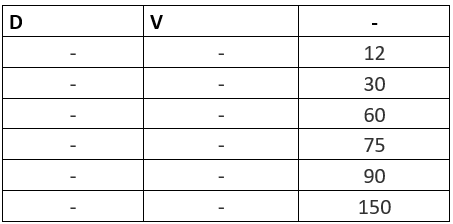
Solution: As it can be observed from the question that the object has fallen 75 meters in 5 seconds, that accounts for the average being 15 meters per second. The initial speed is 0. This means that the average speed for the entire five seconds becomes:
Initial speed+Final speed2
0+Final speed2 = 15
Final Speed= 30.
This is the speed at time t= 5 seconds. Now, it is given that the object is increasing the speed at a uniform rate from 0 to 30 seconds, so at t= 2 seconds, the speed is 12.
So, the average speed over the first two seconds is given as:
Initial speed+Final speed2
If the object moved downward at an average speed of 6 meters/second for 2 seconds, then it covers 12 meters.
v = 30
D = 12
Question 4: P, from Design Solutions, costs $60 per chair. Chair Q, from Seat Unlimited, costs $90 per chair. An office manager often has to buy several chairs to stock the floor space of new offices. On one occasion, she orders p of chair P and q of chair Q. The average cost of a chair would be Average = (60p + 90q )(p + q)
In the table, select a value for p and value for q corresponding to an average cost per chair of $70. Make only two selections, one in each column.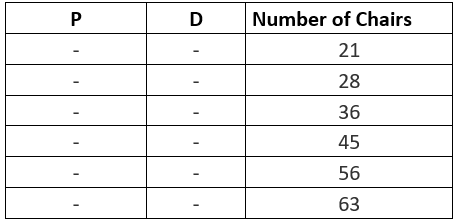
Solution:
Here, it is given that the average is $70, so it means
Average = (60p+ 90q )(p+q)
70= (60p+ 90q )(p+q)
70(p + q) = 60p + 90q
70p + 70q = 60p + 90q
10p + 70q = 90q
10p = 20q
p = 2q
This gives the relationship between p and q. The only numbers that satisfy this relationship are p= 56 and q= 28.
Q5: Two companies are competing against one another for a contract to provide basic vehicle maintenance for another company that maintains a fleet of 300 cars for its sales agents. Jack's Tire and Lube offers on-site maintenance for $42.00 per car.
Care includes basic oil-change services, changing wiper blades and filters as needed, and checking and filling all the car's fluids and tires every 3,000 miles. Major repairs are then referred to a partner company that offers a 20% discount to Jack's clients.
Sam's Service Express offers off-site maintenance for $38.00 per car. Care includes basic oil-changing services, changing wiper blades and filters as needed, and checking and filling all the car's fluids and tires every 3,000 miles. Major repairs are completed by Sam's company at the site where basic maintenance is performed. Sam's offers a 10% discount to contract clients.
Each company requires that a minimum of 100 cars be put on their service. The CEO who must arrange the contracts can see benefits in both service agreements. He has exactly $10,000 to spend on car service contracting. He wants to ensure that the older cars in the fleet are on Jack's service plan. Roughly one-third of the cars in the fleet are more than 2 years old and have high mileage.
How many cars in his fleet should be put on each plan to spend the $10,000 budget exactly? Make only one selection in each column.
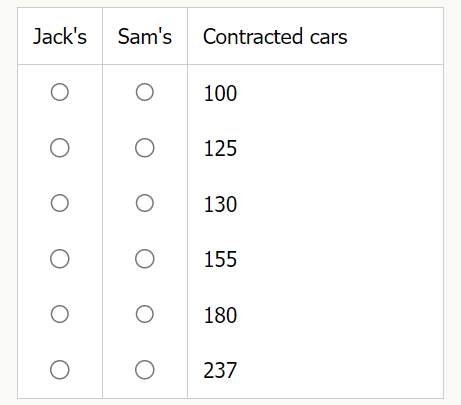
Solution:
The correct answer is 125 cars for each company.
More than one-third of the cars in the fleet must be covered by Jack's service plan. This is the only qualifier for how many cars should be on each plan. So at least 100 cars should be on Jack's plan.
Set up an equation for the total cost of the cars on each service plan, which must equal exactly $10,000 : 38$ + 42J = 10,000. Start with the lowest number, and plug in 100 for S. This equals 38(100) + 42J = 10,000. In this case, J would equal a decimal number, 147.62.
Plug in the next highest number, 125, for $: 38(125) + 427 = 10,000. in this case, J would also equal 125. Both companies would service the same number of cars.
|
24 videos|28 docs|21 tests
|
FAQs on Overview: Two-Part Analysis - Data Insights for GMAT
| 1. What is Two-Part Analysis in GMAT? |  |
| 2. What are the types of GMAT Two-Part Analysis Questions? |  |
| 3. How can I prepare for GMAT Two-Part Analysis questions? |  |
| 4. Can you provide some tips for GMAT Two-Part Analysis preparation? |  |
| 5. Can you provide examples of GMAT Two-Part Analysis questions and explanations? |  |















