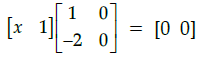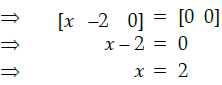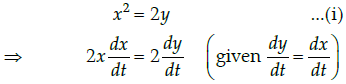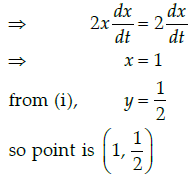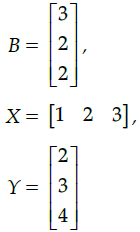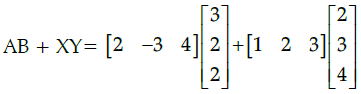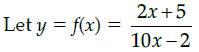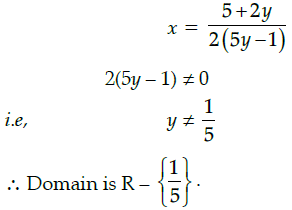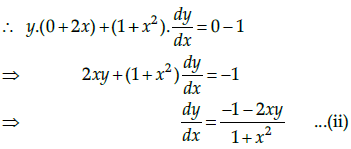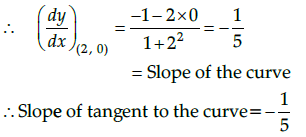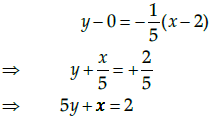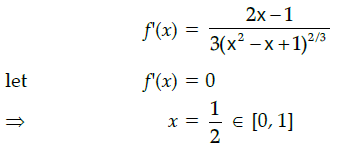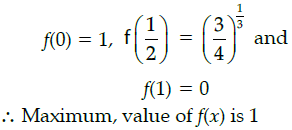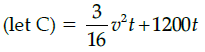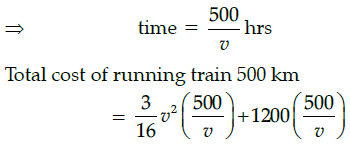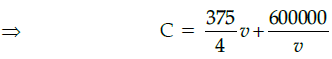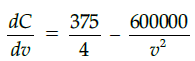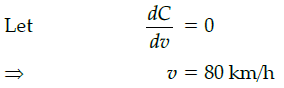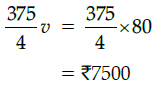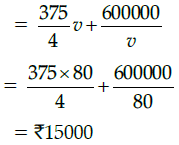Class 12 Mathematics: CBSE Sample Question Paper- Term I (2021-22)- 1 | Mathematics (Maths) Class 12 - JEE PDF Download
| Table of contents |

|
| Class-XII |

|
| Time: 90 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-XII
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- This question paper contains three sections – A, B and C. Each part is compulsory.
- Section - A has 20 MCQs, attempt any 16 out of 20.
- Section - B has 20 MCQs, attempt any 16 out of 20.
- Section - C has 10 MCQs, attempt any 8 out of 10.
- There is no negative marking.
- All questions carry equal marks
Section - A
Q.1: 1. What is the principal value branch of sec–1 x ?
(a) (–1, 1)
(b) [–1, 1]
(c) 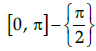
(d) [0, π]
Correct Answer is Option (c)
The sec function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat. For sec function this interval is considered as
Thus when we take the inverse of the function the domain becomes range and the range becomes domain. Hence the principal value branch is the range of sec–1x that is
Q.2: What is the derivative of the function y = xtanx ?
(a) xtanx(xsecx + sec x logx)
(b) 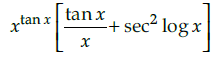
(c) xtanx (2x sec x + tanx log x))
(d) 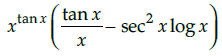
Correct Answer is Option (b)
y = xtan x
log y = tanx logx
Differentiating both side w.r.t. x.
Q.3: Matrix 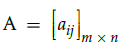 is a square matrix if
is a square matrix if
(a) m > n
(b) m < n
(c) m = 1
(d) m = n
Correct Answer is Option (d)
Given matrix is said to be square matrix if number of rows are equal to number of columns. Therefore,is a square matrix only if m = n.
Q.4: Calculate the determinant of the given matrix 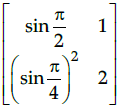
(a) 1/2
(b) -1/2
(c) 3/2
(d) None of the above
Correct Answer is Option (a)
Q.5: Absolute maximum of the function 2x + 5 in [5, 10] ?
(a) 5
(b) 10
(c) 20
(d) 25
Correct Answer is Option (d)
Given, f '(x) = 2x + 5
Therefore, f '(x) = 2 > 0
Since, f '(x) > 0 in the maximum value is at upper and point f(10) = 2 × 10 + 5 = 25
Q.6: if 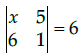 then the value of x is:
then the value of x is:
(a) –6
(b) –36
(c) 6
(d) 36
Correct Answer is Option (d)
For any matrices A and B of suitable orders, we have
(a) (A')' = A
(b) (A + B)' = A' + B'
(c) (kA)' = kA' (where k is any constant)
(d) (A B)' = B'A'
Q.7: Given set A = {a, b, c}. An identity relation in set A is:
(a) R= {(a, b), (a, c)}
(b) R= {(a, a), (b, b), (c, c)}
(c) R= {(a, a), (b, b), (c, c), (a, c)}
(d) R= {(c, a), (b, a), (a, a)}
Correct Answer is Option (b)
Identity relation is function that always returns the same value that was used as its argument. That is, f(x) = x for all elements in set A.
Q.8: For a square matrix A = [aij] the quantity calculated for any element aij in A as the product of (-1)i+j and determinant of the square sub-matrix of order (n-1) obtained by leaving the ith row and jth column of A is known as
(a) Cofactor
(b) Minor
(c) Coefficient
(d) Elements
Correct Answer is Option (a)
The cofactor of an element aij in A is calculated as the product of ( -1)i+j and determinant of the square sub-matrix of order (n-1) obtained by leaving the ith row and jth column of A.
Q.9: What is the absolute minimum of the function |x – 3| in the interval [4, 5] ?
(a) 2
(b) 4
(c) 6
(d) 8
Correct Answer is Option (a)
Since the given function is increasing continuously in the given interval, maximum value is at the extreme end point.
Q.10: What is the general interval for sine function to become a bijective function?
(a) 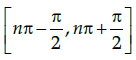
(b) 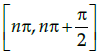
(c) 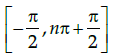
(d) 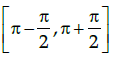
Correct Answer is Option (a)
The sine function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat.
Q.11: Let R be relation from R to R the set of real numbers defined by R = {(x, y): x, y ∈ R and x – y + √3 is an irrational number}. Then, R is:
(a) Reflexive
(b) Transitive
(c) Symmetric
(d) An equivalence relation
Correct Answer is Option (d)
For reflexive, let (x, x) ∈ R
⇒ x - x + √3 = √3 which is an irrational number. Hence, it is reflexive.
For symmetric, let f(x, y) ∈ R
⇒ x - y + √3 which is an irrational number.
This means y - x + √3 is an irrational number. So, f(y, x) ∈ R. Hence, it is symmetric.
For transitive, let f(x, y)∈ R
⇒ x - y + √3 and f(y, z) ∈ R
⇒ y - z + √3. Now adding these equations, we will get x - z + √3
⇒ (x, z)∈ R. Hence, it is transitive. Therefore, it is an equivalence relation.
Q.12: if x = at4, y = at3 then dy/dx will be
(a) 3/4t
(b) 3/4t2
(c) 3/4
(d) 3t/4
Correct Answer is Option (a)
Q.13: Every Identity matrix is a:
(a) Zero matrix
(b) Row matrix
(c) Scalar matrix
(d) Column matrix
Correct Answer is Option (c)
A scalar matrix is an identity matrix when k = 1. But every identity matrix is clearly a scalar matrix.
Q.14: If y = sin x log x then the value of dy/dx is
(a) sin x log x – 1
(b) 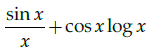
(c) 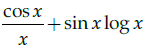
(d) 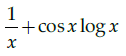
Correct Answer is Option (b)
y = sinx logx
Q.15: For Matrix 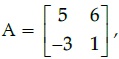 (adj A)' is equal to
(adj A)' is equal to
(a) 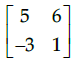
(b) 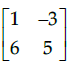
(c) 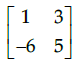
(d) 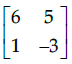
Correct Answer is Option (c)
Q.16: Which of the following line perpendicular to the tangent to curve y = x2 – 5 at x=1.
(a) 2y+x - 35 = 0
(b) 2x−3y+35 = 0
(c) 4x+7y+35 = 0
(d) 3x+7y+21= 0
Correct Answer is Option (a)
Slope of tangent = dy/dx = 2x at x = 1, dy/dx = 2
slope of the perpendicular is - 1/slope
= - 1/2Required equation is 2y + x – 35 =0
Q.17: Calculate the value of x such that the matrix 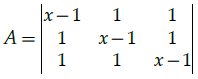 is singular.
is singular.
(a) –1, 2
(b) 2, 3
(c) 1
(d) No such value exist
Correct Answer is Option (a)
+ 1[1 – x + 1] = 0
⇒ (x – 1)(x2 + 1 – 2x – 1) – x + 2 + 2 – x = 0
⇒ (x – 1)(x2 – 2x) – 2(x – 2) = 0
⇒ (x – 2)(x2 – x – 2) = 0
Q.18: If 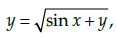 then dy/dx is equal to
then dy/dx is equal to
(a) 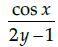
(b) 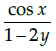
(c) 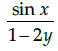
(d) 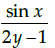
Correct Answer is Option (a)
Given that,
Differentiate with respect to x, we have
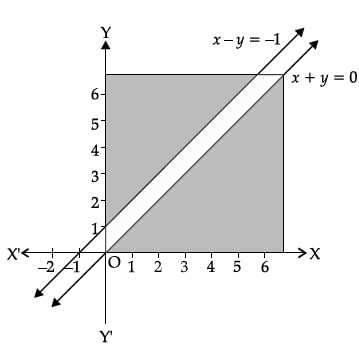
Q.19: Maximize Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
(a) the value of z is minimum at every point on line x – y = –1
(b) there is no feasible region with these constraints.
(c) the value of z is minimum at every point on line –x + y = 1
(d) None
Correct Answer is Option (b)
The region determined by the constraints, is as follows. There is no feasible region and thus, Z has
x – y ≤ –1, –x + y ≤ 0, x, y≥ 0
Q.20: Which of the following is true for the given function?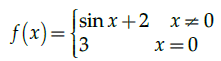
(a) Continuous at x = 0
(b) Not continuous at 0
(c) differentiable at 0
(d) None of the above
Correct Answer is Option (b)
Given,
Section - B
Q.21: Let A = {a, b, c} and B = {1, 2, 3} and f: A→ B is defined by f = {(a, 2), (b, 1), (c, 3)}. Is the function oneone and onto.
(a) both one-one and onto
(b) only one-one
(c) only onto
(d) neither of them
Correct Answer is Option (a)
All the elements in the domain has a unique value in the range. Also the codomain of the function is equal to its range.
Q.22: Find the dy/dx of yx+xy = 0 ?
(a) 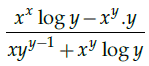
(b) 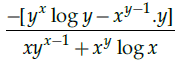
(c) 0
(d) None of these
Correct Answer is Option (b)
yx+xy = 0
or exlogy + eylogx = 0
Differentiating both sides w.r.t. x.
Q.23: Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function.
The minimum value of F occurs at
(a) (0, 2) only
(b) (3, 0) only
(c) the mid-point of the line segment joining the points (0, 2) and (3, 0) only
(d) any point on the line segment joining the points (0, 2) and (3, 0)
Correct Answer is Option (d)
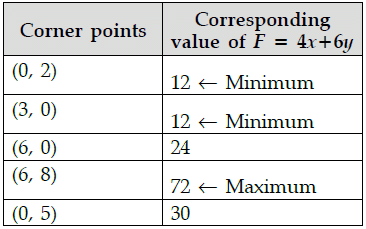
Hence, minimum value of F occurs at any points on the line segment joining the points (0, 2) and (3, 0).
Q.24: Consider the curve y = x2/4. The Slope of the line parallel to tangent to the curve at x = 1 is
(a) 1/4
(b) 1/3
(c) - 1/2
(d) 1/2
Correct Answer is Option (d)
y = x2/4
Slope of the curve
Parallel lines have same slopes
∴ Slope of tangent = 1/2
Q.25: if 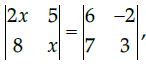 then the value of x is
then the value of x is
(a) 3
(b) ±3
(c) ±6
(d) 6
Correct Answer is Option (c)
The process described in the reason statement is the correct procedure to solve the given question. For the given determinant,
2x2 – 40 = 32
2x2 = 72
x = ±6
Q.26: Given a function f (x)= 2x3 −21x2 +60x+48, it has local maximum at x =
(a) 2
(b) 3
(c) 5
(d) 4
Correct Answer is Option (a)
f(x) = 2x3 – 21x2 + 60x + 48
f'(x) = 6x2 – 42x + 60
f'(x) = 0
⇒ 6x2 – 42x + 60 = 0
6 (x2 – 7x + 10) = 0
6 (x – 2) (x – 5) = 0
x = 2, 5f''(x) = 12x – 42
f''(2) = –18 < 0
f''(5) = 60 – 42
= 18 > 0∴ f(x) is maximum at x = 2.
Q.27: The principal value of 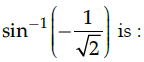
(a) π/4
(b) π/6
(c) -π/4
(d) π/3
Correct Answer is Option (c)
The principal value of
means that we need to find an angle in the principal branch of the function where the sine function is equal to - 1/√2. Hence the required value is -π/4.
Q.28: Suppose P and Q are two different matrices of order 3 × n and n × p, then the order of the matrix P × Q is ?
(a) 3 × p
(b) p × 3
(c) n × n
(d) 3 × 3
Correct Answer is Option (a)
Q.29: Let f(x) = |sin x|, then
(a) f is everywhere differentiable
(b) f is everywhere continuous but not differentiable at x = n π, n ∈ Z.
(c) f is everywhere continuous but not differentiable at 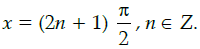
(d) none of these
Correct Answer is Option (b)
Given that, f(x) = |sin x|
The functions |x| and sin x are continuous function for all real value of x.
Thus, the function f(x) = |sin x| is continuous function everywhere.
Now, |x| is non-differentiable function at x = 0.
Since f(x) = |sin x| is non-differentiable function at sin x = 0
Thus, f is everywhere continuous but not differentiable at x = n π, n ∈ Z.
Q.30: If function f : R → R defined as f(x) = x2 then f(x) is
(a) onto
(b) one-one and onto
(c) one-one
(d) None of these
Correct Answer is Option (d)
f(x) is a one-one function
if f(x1) = f(x2) ⇒ x1= x2
Let f(x1) = f(x2) for some x1, x2 ∈ R
⇒(x1)2=(x2)2
⇒ x1 = ±x2
Hence f(x) is one-one.
Q.31: Which of these intervals, the function f (x)= √2 cos x+x−35 is monotonic?
(a) 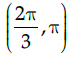
(b) 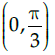
(c) 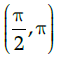
(d) 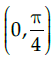
Correct Answer is Option (d)
A function is Monotonic if its first derivative’s sign doesn’t change in the given interval.
Q.32: If 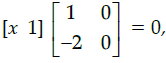 then x equals
then x equals
(a) 0
(b) -2
(c) -1
(d) 2
Correct Answer is Option (d)
Q.33: Objective function:
Maximise Z = 1000x + 600y
Constraints:
x + y ≥ 200
y ≥ 20, x ≥ 0
y ≥ 4x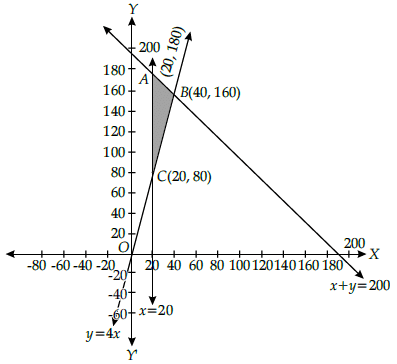
Z is maximum at point
(a) (20, 80)
(b) (20, 180)
(c) (0, 0)
(d) (40, 160)
Correct Answer is Option (d)
The corner points are A(20, 180), B(40, 160), C(20, 80)
Evaluating the objective function Z = 1,000x + 600y at A, B and C
At A(20, 180),
Z = 1,000 × 20 + 600 × 180 = 20,000 + 1,08,000 = ₹1,28,000
At B(40, 160), Z = 1,000 × 40 + 600 × 160 = 40,000 + 96,000 = ₹1,36,000 (max.)
At C(20, 80), Z = 1000 × 20 + 600 × 80 = 20,000 + 48,000 = ₹68,000 or
Z is maximum, when x = 40, y = 160.
Q.34: A particle moves along the curve x2 = 2y. The point at which, ordinate increases at the same rate as the abscissa is ________
(a) (1,2)
(b) (1/2, 1)
(c) (1/2, 1/2)
(d) (1, 1/2)
Correct Answer is Option (d)
Q.35: If 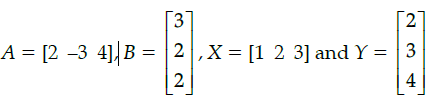 then AB + XY equals
then AB + XY equals
(a) [28]
(b) [24]
(c) 28
(d) 24
Correct Answer is Option (a)
Given, A = [2 -3 4] ,= [6 – 6 + 8] + [2 + 6 + 12]
= [8] + [20]
= [28]
Q.36: If function 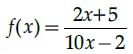 Then the domain of the function is:
Then the domain of the function is:
(a) 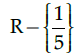
(b) R
(c) R - {1}
(d) R - {5}
Correct Answer is Option (a)
10xy – 2y = 2x + 5
10xy – 2x = 5 + 2y2x(5y – 1) = 5 + 2y
Q.37: The maximum number of equivalence relations on the set A = {1, 2, 3} are
(a) 1
(b) 2
(c) 3
(d) 5
Correct Answer is Option (d)
Given that, A = {1, 2, 3}
Now, number of equivalence relations are as follows:
R1 = {(1, 1), (2, 2), (3, 3)}
R2 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
R3 = {(1, 1), (2, 2), (3, 3), (1, 3), (3, 1)}
R4 = {(1, 1), (2, 2), (3, 3), (2, 3), (3, 2)}
R5 = {(1, 2, 3) ⇔ A × A = A2}
∴ Maximum number of equivalence relations on the set A = {1, 2, 3} = 5
Q.38: If A is any square matrix of order 3 × 3 such that |A| = 3, then the value of |adj A| is?
(a) 3
(b) 1/3
(c) 9
(d) 27
Correct Answer is Option (c)
|A| = 3, n = 3
|adj A| = |A|2 = 32 = 9
Q.39: The equation of tangent to the curve y(1 + x2) = 2 – x, where it crosses x-axis is:
(a) x + 5y = 2
(b) x – 5y = 2
(c) 5x – y = 2
(d) 5x + y = 2
Correct Answer is Option (a)
Given that the equation of curve is
y(1 + x2) = 2 – x ...(i)
On differentiating with respect to x, we get
Since, the given curve passes through -axis,
i.e y = 0
∴ 0(1 + x2) = 2 - x [by using eq. (i) ]
⇒ x = 2
So the curve passes through the point (2, 0).
∴ Equation of tangent to the curve passsing through (2, 0) is
Q.40: A = [aij]m×n is a square matrix, if
(a) m < n
(b) m > n
(c) m = n
(d) None of these
Correct Answer is Option (c)
It is known that a given matrix is said to be a square matrix if the number of rows is equal to the number of columns.
Therefore,
A = [aij]m x n is a square matrix, if m = n.
Section - C
Q.41: For an objective function Z = ax + by, where a, b > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
(a) b − 3a = 0
(b) a = 3b
(c) a + 2b = 0
(d) 2a − b = 0
Correct Answer is Option (a)
As Z is maximum at (30, 30) and (0, 40)
⇒ 30a + b = 40b
⇒ b – 3a = 0
Q.42: For which value of m is the line y = mx + 1 a tangent to the curve y2 = 4x?
(a) 1 2
(b) 1
(c) 2
(d) 3
Correct Answer is Option (b)
y = mx + 1 ...(i)
and y2 = 4x ...(ii)
Substituting (i) in (ii) :(mx + 1)2 = 4x
⇒ m2x2 + (2m – 4)x + 1 = 0 ...(iii)
As line is tangent to the curve⇒ line touches the curve at only one point
⇒ (2m – 4)2 – 4m2 = 0
⇒ m = 1
Q.43: The maximum value of [x(x+1)+1]1/3, 0 ≤ x ≤ 1 is:
(a) 0
(b) 1/2
(c) 1
(d) 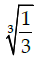
Correct Answer is Option (c)
Let f(x) = [x(x – 1) + 1]1/3,0 ≤ x ≤ 1
Q.44: In a linear programming problem, the constraints on the decision variables x and y are x − 3y ≥ 0, y ≥ 0, 0 ≤ x ≤ 3. The feasible region
(a) is not in the first quadrant
(b) is bounded in the first quadrant
(c) is unbounded in the first quadrant
(d) does not exist
Correct Answer is Option (b)
Feasible region is bounded in the first quadrant
Q.45: Let 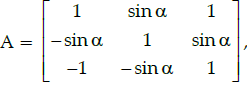 where 0 ≤ α ≤ 2π, then:
where 0 ≤ α ≤ 2π, then:
(A) |A|= 0
(B) |A| ∈ (2, ∞)
(C) |A| ∈ (2, 4)
(D) |A| ∈ [2, 4]
Correct Answer is Option (d)
|A| = 2 + 2sin2θ
As –1 ≤ sin θ ≤ 1, ∀ 0 ≤ θ ≤ 2π
⇒ 2 ≤ 2 + 2sin2θ ≤ 4
⇒ |A|∈ [2, 4]
Questions 46-50 are based on a Case-Study
Case-Study
The fuel cost per hour for running a train is proportional to the square of the speed it generates in km per hour. If the fuel costs ₹48 per hour at speed 16 km per hour and the fixed charges to run the train amount to ₹1200 per hour. Assume the speed of the train as v km/h. Based on the given information, answer the following questions.
Q.46: Given that the fuel cost per hour is k times the square of the speed the train generates in km/h, the value of k is:
(a) 16/3
(b) 1/3
(c) 3
(d) 3/16
Correct Answer is Option (d)
Fuel cost = k(speed)2
⇒ 48 = k.162
⇒ k = 3/16
Q.47: If the train has travelled a distance of 500km, then the total cost of running the train is given by function:
(a) 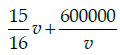
(b) 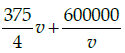
(c) 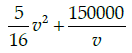
(d) 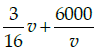
Correct Answer is Option (b)
Total cost of running train
Distance covered = 500 km
Q.48: The most economical speed to run the train is:
(a) 18km/h
(b) 5km/h
(c) 80km/h
(d) 40km/h
Correct Answer is Option (c)
Q.49: The fuel cost for the train to travel 500 km at the most economical speed is: (a) ₹3750
(b) ₹750
(c) ₹7500
(d) ₹75000
Correct Answer is Option (c)
Fuel cost for running 500 km
Q.50: The total cost of the train to travel 500km at the most economical speed is:
(a) ₹3750
(b) ₹75000
(c) ₹7500
(d) ₹15000
Correct Answer is Option (d)
Total cost for running 500 km
|
204 videos|290 docs|139 tests
|

|
Explore Courses for JEE exam
|

|
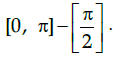
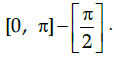
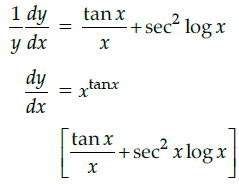
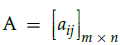 is a square matrix only if m = n.
is a square matrix only if m = n.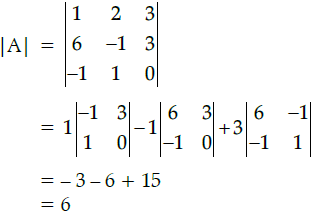
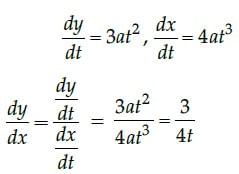
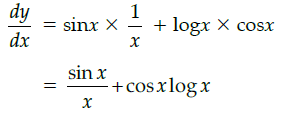
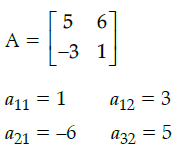
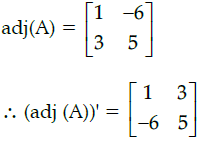
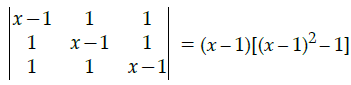
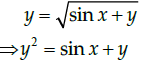
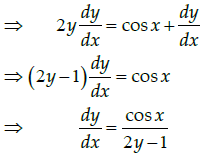
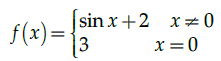
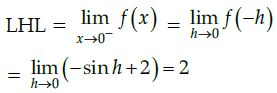
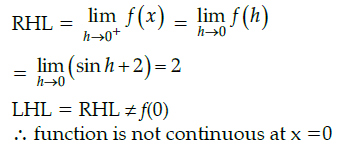
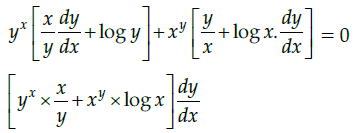
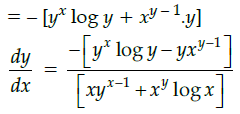
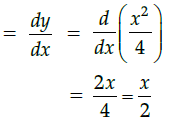

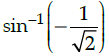 means that we need to find an angle in the principal branch of the function where the sine function is equal to - 1/√2. Hence the required value is -π/4.
means that we need to find an angle in the principal branch of the function where the sine function is equal to - 1/√2. Hence the required value is -π/4.