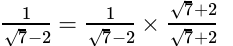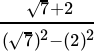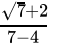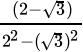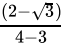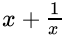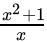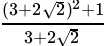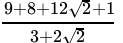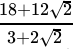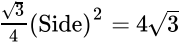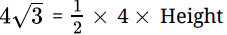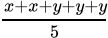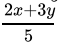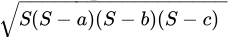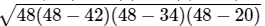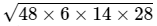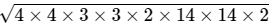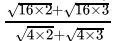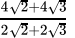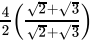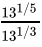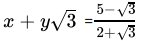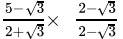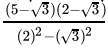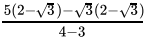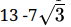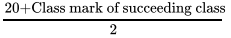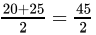Class 9 Math: Sample Question Paper Term I- 4 (With Solutions) | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Class 09 Mathematics |

|
| Time: 90 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class 09 Mathematics
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- The question paper contains three parts A, B and C
- Section A consists of 20 questions of 1 mark each. Attempt any 16 questions
- Section B consists of 20 questions of 1 mark each. Attempt any 16 questions.
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Section - A
Q.1: The number obtained on rationalising the denominator of 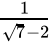 is
is
(a) 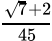
(b) 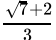
(c) 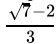
(d) 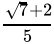
Correct Answer is Option (b)
After rationalising
=
=
=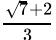
Q.2: Which of the following pair is a solution of the equation 3x – 2y = 7?
(a) (-2, 1)
(b) (1, -2)
(c) (5, 1)
(d) (1, 5)
Correct Answer is Option (b)
Solution of the equation 3x – 2y = 7 is (1, -2) as it satisfy the given equation
3x – 2y = 7
⇒ 3(1) - 2(-2) = 7
⇒ 3 + 4 = 7
LHS = RHS
Q.3: If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
(a) an isosceles triangle
(b) an equilateral triangle
(c) a right triangle
(d) an obtuse angled triangle
Correct Answer is Option (c)
The sum of the angles of triangle is 180o.
let the angles of triangle be a, b, c
We have given that one angle of a triangle is equal to the sum of the other two angles
so we have
c = a + b
a + b + c = 180o
Substitute c for a + b
c + c = 180o
2c = 180o
c = 90o
Therefore the triangle is a right triangle.
Q.4: The area of an isosceles right angled triangle of equal side 30 cm, is given as
(a) 45 cm2
(b) 900 cm2
(c) 450 cm2
(d) 225√3 cm2
Correct Answer is Option (c)
Area of triangle = 1/2 x Base x Height
= 1/2 x 30 x 30 = 450 sq. cm
Q.5: The value of x - yx-y when x = 2 and y = -2, is
(a) 14
(b) -18
(c) 18
(d) -14
Correct Answer is Option (d)
x = 2, y = -2
x - yx-y = 2 - (-2)2-(-2)
= 2 - (-2)2+2
= 2 - (-2)4
= 2- (+16)
= 2 - 16
= -14
Q.6: The graph of the linear equation 2x + 3y = 6 cuts the y-axis at the point
(a) (2, 0)
(b) (3, 0)
(c) (0, 2)
(d) (0, 3)
Correct Answer is Option (c)
where x- coordinate is zero
2(0) + 3y = 6 ⇒ 3y = 6 ⇒ y = 6 + 3 = 2
So, (0,2) is the required point.
Q.7: The points (-5,3) and (3, -5) lie in the
(a) IV and II quadrants respectively
(b) II and IV quadrants respectively
(c) same quadrant
(d) II and III quadrants respectively
Correct Answer is Option (b)
II and IV quadrants respectively, as in II quadrant abscissa is negative and ordinate in positive, on the other hand in IV quadrant abscissa is positive and ordinate is negative.
Q.8: In a triangle ΔABC, ∠B = 35o and ∠C = 60o, then the shortest side is
(a) BC
(b) AB
(c) AB and BC
(d) AC
Correct Answer is Option (d)
Side opposite to smallest angle is shortest side angles of triangle are 35,60 and 85
Q.9: If a = 2 + √3 , then the value of 1/a is
(a) 2 + √3
(b) 2 - √3
(c) √3 - 2
(d) 1
Correct Answer is Option (b)
x = 2 + √3
=
=
=
= 2 - √3
Q.10: The sum of two angles of a triangle is equal to its third angle. Find the third angle.
(a) 70o
(b) 90o
(c) 45o
(d) 60o
Correct Answer is Option (b)
In Triangle ABC
Let the sum of two angles = x
Therefore, the third angle = x (Given)
Applying angle sum property
(sum of two angles) + (Third angle) = 180o
x + x = 180°
2x = 180°
x = 180°/2
x = 90°
i.e Third angle = 90°
Q.11: In fig if x = 30° then y =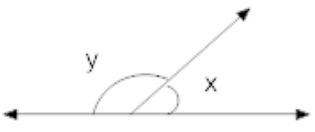
(a) 210°
(b) 180°
(c) 90°
(d) 150°
Correct Answer is Option (d)
x + y = 180° (linear pair)
x = 30°
30° + y = 180°
y = 180° - 30°
y = 150°
Q.12: A rational number equivalent to a rational number 7/19 is
(a) 17/119
(b) 21/57
(c) 14/57
(d) 21/58
Correct Answer is Option (b)
Divide numerator and denominator by 3
Q.13: If x = 3 + √2, then the value of x + 1/x is
(a) 0
(b) 3
(c) 1
(d) 6
Correct Answer is Option (d)
⇒
Put the value of x,
⇒
⇒
⇒
⇒
⇒ 6
Q.14: The point (7, 0) lies
(a) on the positive direction of y-axis
(b) on the positive direction of x-axis
(c) in quadrant IV
(d) in quadrant II
Correct Answer is Option (b)
Since value of y-ordinate is zero so, point lies on x-axis.
But value of x is +ve so it lies on +ve direction of x-axis.
Q.15: The graph of the line y = −3 does not pass through the point.
(a) (3, −3)
(b) (−3, 2)
(c) (0, −3)
(d) (2, −3)
Correct Answer is Option (b)
The graph of the line y = -3 does not pass through (-3, 2) since (-3, 2) does not satisfy y = -3.
Q.16: In the given fig., if ABCD is a quadrilateral in which AD = BC, AB = CD, and ∠D = ∠B, then ∠CAB is equal to
(a) ∠BAC
(b) ∠ACD
(c) ∠CAD
(d) ∠ABC
Correct Answer is Option (b)
∠ACD is the right answer;
In ΔACD and ΔCAB
AD = BC (Given)
∠D = ∠B (Given)
AB = CD (Given)
∴ ΔACD ≅ ΔCAB ( by SAS congruence criteria),
⇒ ∠CAB = ∠ACD (cpct)
Q.17: The area of an equilateral triangle of side a is 4√3 cm2. Its height is given by
(a) 2 /√3 cm
(b) 2√3 cm
(c) 1/3 cm
(d) √3 cm
Correct Answer is Option (b)
Area of equilateral triangle = √3/4 (Side)2
⇒
⇒ (Side)2 = 42
⇒ Side = 4 cm
Area of triangle = 1/2 x Base x Height
⇒
⇒ Height = 2√3 cm
Q.18: Sheila received x marks in two of her tests and y marks in three other tests. Her average score in all the five tests in terms of x and y is
(a) 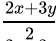
(b) 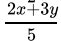
(c) 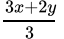
(d) 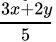
Correct Answer is Option (b)
Average is equal to the sum of all the values in the data set divided by the number of values in the data set.Average =
Average =
Q.19: The value of 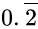 in the form where p/q and q are integers and q ≠ 0 is
in the form where p/q and q are integers and q ≠ 0 is
(a) 2/9
(b) 1/5
(c) 2/5
(d) 1/8
Correct Answer is Option (a)
Let x= 0.222...---(i)
multiply eq. (i) by 10, we get
10 x = 2.222....---(ii)
10 x - x = 2.222...-0.222...
9x = 2
x = 2/9
Q.20: A point whose abscissa is -3 and ordinate 2 lies in
(a) second quadrant
(b) fourth quadrant
(c) first quadrant
(d) third quadrant
Correct Answer is Option (a)
As we know that abscissa is negative in second and third coordinate and ordinate is positive in first and second coordinate. Therefore the given point (-3, 2) lies in second coordinate.
Section - B
Q.21: The distance between the graphs of the equations y = -2 and y = -5
(a) 7
(b) 3
(c) None of these
(d) -7
Correct Answer is Option (b)
Distance between the graphs of y = -2, and y = -5 is equivalent to the distance between the points P(0, -2) and Q(0, -5). This is given by
|PQ| == 3
Q.22: The height corresponding to the longest side of the triangle whose sides are 42 cm, 34 cm and 20 cm in length is.
(a) 36 cm
(b) 15 cm
(c) 23 cm
(d) 16 cm
Correct Answer is Option (d)
Here, a = 42 cm, b = 34 cm and c = 20 cm
Therefore,= 48
Area =
=
=
=
= 4 x 3 x 2 x 14
= 336 cm2Longest side = 42 cm
⇒ b = 42 cm
Let h be the height corresponding to the longest side.
Area of the triangle = 1/2 x b x h
⇒ 1/2 x b x h = 336
⇒ 42 x h = 336 x 2
⇒ h = 336 x 2 / 42 = 16cm
Q.23: If we divide both sides of a linear equation with a non-zero number, then the solution of the linear equation
(a) changes
(b) remains the same
(c) none of these
(d) gets divided by the number
Correct Answer is Option (b)
If then for any non-zero c. We can divide both sides of an equation by a non-zero number c, without changing the equation.
Q.24: If x < 0 and y > 0, then the point (x, y) lies in
(a) I Quadrant
(b) II Quadrant
(c) IV Quadrant
(d) III Quadrant
Correct Answer is Option (b)
Here, x < 0 (i.e -ve) and y > 0, (i.e, +ve)
So in 2nd quadrant value of (x , y) is (-, +).
So the given point will lie in 2nd quadrant.
Q.25: 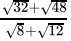 is equal to
is equal to
(a) 8
(b) 2
(c) 4
(d) √2
Correct Answer is Option (b)
⇒
⇒
⇒
⇒ 2
Q.26: Area of the given triangle is
(a) 60 cm2
(b) 32.5 cm2
(c) 78 cm22
(d) 30 cm2
Correct Answer is Option (d)
In the given triangle,
Base (BC) == 5 cm
Area of triangle ABC = 1/2 x BC x AB
= 1/2 x 5 x 12
= 30 sq. cm
Q.27: In ΔABC, ∠A = 50o, ∠B = 60o, Find the longest side of the triangle
(a) BC
(b) Cannot be determined
(c) CA
(d) AB
Correct Answer is Option (d)
By angle sum property, we have,
∠A + ∠B + ∠C = 180°
⇒ 50° + 60° + ∠C = 180°
⇒ ∠C = 180° - (50°+ 60°) = 70°
Therefore, C is the largest angle in the triangle and the side opposite to it i.e. AB is the longest side.
Q.28: Which of the following statement is true?
(a) 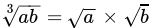
(b) 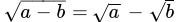
(c) 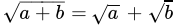
(d) 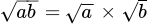
Correct Answer is Option (d)
When we multiply two different root number then only number is multiplied not the root because we have both number power equal,
√a × √b = √ab
Or, a½ × b½ = (ab)½
Q.29: The area of ΔAOB having vertices A(0, 6), 0(0, 0) and B(6, 0) is
(a) 36 sq units
(b) 18 sq units
(c) 12 sq units
(d) 24 sq units
Correct Answer is Option (b)
When we plot the given points in the graph paper then,
ΔAOB is the right angle triangle, where
OB = Base = 6 units
Height of triangle = OA = 6 units
∴ Area of ΔAOB = 1/2 x OA x OB
⇒ Area of ΔAOB = 1/52 x 6 x 6
⇒ Area of ΔAOB = 1/2 x 36
⇒ Area of ΔAOB = 18 sq units
Q.30: Which of the following variables are discrete?
(A) Size of shoes,
(B) Number of pages in a book,
(C) Distance travelled by a train,
(D) Time
(a) B and D
(b) A and C
(c) A and D
(d) A and B
Correct Answer is Option (d)
Discrete variables are variables that can only take finite values.
Size of shoes and pages in the book have a finite number.
Q.31: Length of perpendicular drawn on smallest side of scalene triangle is
(a) largest
(b) No relation
(c) smallest
(d) Equal
Correct Answer is Option (a)
Length of the perpendicular drawn on the smallest side of the scalene triangle is largest.
Q.32: After simplification, 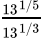 is
is
(a) 138/15
(b) 132/15
(c) 13-2/15
(d) 131/3
Correct Answer is Option (c)
= 131/5 + 1/3
= 13-2/15
Q.33: In the adjoining figure, AB = BC and ∠ABD = ∠CBD, then another angle which measures 30° is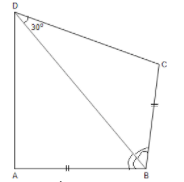
(a) ∠BCA
(b) ∠BCD
(c) ∠BDA
(d) ∠BAD
Correct Answer is Option (c)
In triangle ABD and CBD
AB = BC and ∠ABD = ∠CBD (Given)
BD (Common)
Therefore In triangle ABD and CBD are congruent by SAS criteria.
Therefore, ∠BDA = 30o (by CPCT)
Q.34: Which of the following is not a measure of central tendency?
(a) Mean
(b) Median
(c) Mode
(d) Standard deviation
Correct Answer is Option (d)
A measure of central tendency is a single value that attempts to describe a set of data.
Mean, median and mode are the measures of central tendency.
Standard deviation is not the measure of central tendency.
Q.35: In the given figure x = 30°, the value of Y is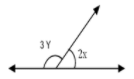
(a) 45°
(b) 40°
(c) 10°
(d) 36°
Correct Answer is Option (b)
In the given figure we have
3Y + 2X = 180° (Linear - Pair)
X = 30°
3Y + 2 30° = 180°
3Y + 60° = 180°
3|Y = 180° - 60°
3Y = 120°
Y = 120°/3
Y = 40°
Q.36: If x = 3 and y = -2 satisfies 5x - y = k, then the value of k is
(a) 3
(b) 17
(c) 12
(d) -2
Correct Answer is Option (b)
If x = 3 and y = -2 satisfies 5x - y = k
Then
5x - y = k
5 3 - (-2) = k
15 + 2 = k
k = 17
Q.37: The sides BC, CA and AB of ΔABC have been produced to D, E and F respectively. ∠BAE + ∠CBF + ∠ACD = ?
(a) 240°
(b) 360°
(c) 300°
(d) 320°
Correct Answer is Option (b)
We have :
∠1 + ∠BAE = 180° ....(i)
∠2 + ∠CBF = 180° ....(ii)
∠3 + ∠ACD = 180° ....(iii)
Adding (i),(ii) and (iii), we get:
(∠1 + ∠2 + ∠3) + (∠BAE + ∠CBF + ∠ACD) = 540°
⇒ 180° + (∠BAE + ∠CBF + ∠ACD) = 540° [ ∴ ∠1 + ∠2 + ∠3 = 180°]
⇒ ∠BAE + ∠CBF + ∠ACD = 540° - 180° = 360°
Q.38: If  , then
, then
(a) x = -13, y = - 7
(b) x = 13, y = -7
(c) x = -13, y = 7
(d) x = 13, y = 7
Correct Answer is Option (b)
=
=
=
=
Hence, x+y√3 =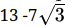
⇒ x = 13, y = -7
Q.39: If ΔPQR ≌ ΔLMN then NL= ________
(a) PQ
(b) QR
(c) RP
(d) None of these
Correct Answer is Option (c)
RP [Follows from definition of congruent triangles]
Q.40: The class marks of a frequency distribution are given as follows 15, 20, 25 the class corresponding to the class mark 20 is
(a) 19.5 - 20.5
(b) 12.5 - 17.5
(c) 18.5 - 21.5
(d) 17.5 - 22.5
Correct Answer is Option (d)
Clearly, Lower limit of the class corresponding to class mark 20
== 17.5
Upper limit of the class corresponding to the class mark 20
=
=
= 22.5
Hence the required class is 17.5 - 22.5
Section - C
Question No. 41 to 45 are based on the given text. Read the text carefully and answer the questions:
Reeta and Rohan were playing a game on parallel lines and the angles formed with the transverse line(ie alternate angles, corresponding angle and interior angles).
First Reeta drew a straight line AB, then Rohan drew another straight line CD||AB. Further, a transverse line PQ was drawn which intersects lines AB and CD at points X and Y respectively.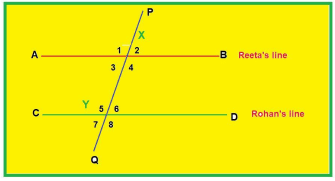 Now they did toss with a coin and Rohan won the toss. Following were the rules of the game:
Now they did toss with a coin and Rohan won the toss. Following were the rules of the game:
i. Toss winner will ask a question and others will answer.
ii. If the answer is correct then person answering will ask question else questioner will ask next question.
iii. Who wins the last question he/she will be the winner.
iv. Total of 5 questions will be asked.
Q.41: Which is the alternate angle to ∠6?
(a) ∠1
(b) ∠3
(c) ∠2
(d) ∠4
Correct Answer is Option (a)
∠1
Q.42: Which is the corresponding angle to ∠1?
(a) ∠4
(b) ∠6
(c) ∠7
(d) ∠5
Correct Answer is Option (d)
∠5
Q.43: If ∠4 = 120° then what is measure of ∠6?
(a) 120°
(b) 80°
(c) 100°
(d) 60°
Correct Answer is Option (d)
60°
Q.44: What is the sum of ∠3 and ∠5?
(a) 60°
(b) 160°
(c) 180°
(d) 100°
Correct Answer is Option (c)
180°
Q.45: ∠5 is equal to which of the following pair of angles?
(a) ∠7 and ∠8
(b) ∠6 and ∠4
(c) ∠4 and ∠8
(d) ∠6 and ∠7
Correct Answer is Option (c)
∠4 and ∠8
Question No. 46 to 50 are based on the given text. Read the text carefully and answer the questions:
The weights of newborn babies (in kg.) are recorded to maintain the health report cards in Apollo hospital on regular basis. On a particular day the weights of newborn recorded are are as follows:
3.1, 3.0, 2.9, 2.9, 2.8, 2.8, 2.7, 2.7, 2.6, 2.5, 2.5, 2.4, 2.3, 2.2, 2.1.
Q.46: Determine the range.
(a) 1.0 Kg
(b) 2.0 Kg
(c) 2.7 Kg
(d) 2.1 Kg
Correct Answer is Option (a)
1.0 Kg
Q.47: How many babies were born on that day?
(a) 12
(b) 11
(c) 16
(d) 15
Correct Answer is Option (d)
15
Q.48: How many babies weigh below 2.5 kg?
(a) 6
(b) 3
(c) 5
(d) 4
Correct Answer is Option (d)
4
Q.49: How many babies weigh more than 2.8 kg?
(a) 2
(b) 1
(c) 3
(d) 4
Correct Answer is Option (d)
4
Q.50: How many babies weigh 2.8 kg
(a) 2
(b) 1
(c) 3
(d) 4
Correct Answer is Option (a)
2
|
40 videos|471 docs|57 tests
|