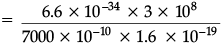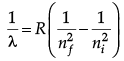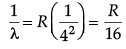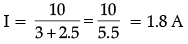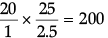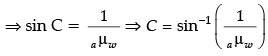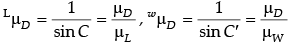Class 12 Physics: CBSE Sample Question Paper- Term II (2021-22)- 1 | Sample Papers for Class 12 Medical and Non-Medical PDF Download
| Table of contents |

|
| Class-XII |

|
| Time: 120 Minutes |

|
| Max. Marks: 35 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-XII
Time: 120 Minutes
Max. Marks: 35
General Instructions :
- There are 12 questions in all. All questions are compulsory.
- This question paper has three sections: Section A, Section B and Section C.
- Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
- There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the choices in such questions.
- You may use log tables if necessary but use of calculator is not allowed.
Section - A
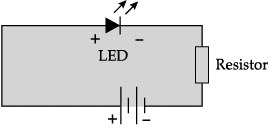
Q.1. Explain with help of circuit diagram, the action of a forward biased p-n junction diode which emits spontaneous radiation. State the least band gap energy of this diode to have emission in visible region.
Circuit diagram showing biasing of LED in forward bias
Action of LED
For emission in visible range least band energy required is 1.8 eVDetailed Answer:
When Light Emitting Diode (LED) is forward biased, free electrons in the conduction band recombines with the holes in the valence band and releases energy in the form of light.
The wavelength of electromagnetic radiation for it to lie in the visible region should lie in the range of 4000Å−7000Å.
Band gap energy = hc/λ
= 1.77 eV
Q.2. State Bohr ’s quantization condition of angular momentum. Calculate the shortest wavelength of the Brackett series and state to which part of the electromagnetic spectrum does it belong.
OR
A photon emitted during the de-excitation of electron from a state n to the first excited state in a hydrogen atom, irradiates a metallic cathode of work function 2 eV, in a photo cell, with a stopping potential of 0.55 V. Obtain the value of the quantum number of the state n.
Statement of Bohr ’s quantization condition
Calculation of shortest wavelength
Identification of part of electromagnetic spectrum
Electron revolves around the nucleus only in those orbits for which the angular momentum is some integral of h/2π. (where h is Planck’s constant)
Also give full credit if a student write mathematically mvr = nh/2π.
For Brackett Series,
Shortest wavelength is for the transition of electrons from ni = ∞ to nf = 4
λ = (16/R)m
= 1458.5 nm on substitution of value of R Infrared region.[Note: Don’t deduct any mark for this part, when a student does not substitute the value of R, to calculate the numerical value of λ]
OR
For writing Einstein's photoelectric equation
For writing, En = -(13.6/n2)
For finding the value of n
hv = φ0 + eVs
= 2 + 0.55 = 2.55 eV
Given, En = 13.6/n2
The every difference, ΔE = E2 - E1
E2 = -(1.36 /((2)2)) = -3.4 eV,
E1 = – 2.55 eV
ΔE = – 3.4 – (– 2.55) eV = – 0.85 eV
∴ (-136)/n2 = - 0.85
∴ n = 4
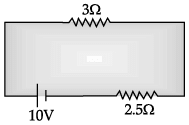
Q.3. Assuming that the two diodes D1 and D2 used in the electric circuit shown in the figure are ideal, find out the value of the current flowing through 2.5 Ω resistor.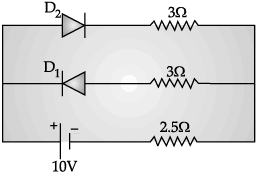
In the circuit, if D1 is open and D2 is short, then equivalent circuit will result as:
D2 is reverse biased
∴ D1 conductscurrent in 2.5 W resistance
I = (E/(3+2.5))A
Section - B
Q.4. The ground static energy of H-atom in –13.6 eV. Calculate the kinetic and potential energies of the election for the same state.
Kinetic energy,
...(i)
Potential energy, U = -
...(ii)
Total energy E = K + U = -...(iii)
Comparing equations (i), (ii), (iii), we have
K = –E and U = 2E
Given E = –13.6 eV (in ground state)
∴ Kinetic energy, K = 13.6 eV
Potential energy U = 2 × (–13.6 eV) = –27.2 eV.
Q.5. (a) Distinguish between n-type and p-type semiconductor on the basis of energy band diagram.
(b) Compare their conductivities at absolute zero temperature and at room temperature.
(a)
(b) At absolute zero temperature, conductivities of both type of semi-conductors are zero.
At normal room temperature, for equal doping, conductivity of n-type semiconductor is more than that of p-type semiconductor.
Q.6. (a) Give one point of difference between nuclear fission and nuclear fusion.
(b) Suppose we consider fission of a 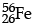 into two equal fragments of
into two equal fragments of 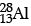 nucleus. Is the fission energetically possible? Justify your answer by working out Q value of the process.
nucleus. Is the fission energetically possible? Justify your answer by working out Q value of the process.
Given (m)  = 55.93494 u and (m)
= 55.93494 u and (m)  = 27.98191 u
= 27.98191 u
(a) Difference between nuclear fission and nuclear fusion: (any one)
(i) Fission is the splitting of a large atom into two or more smaller ones.
Fusion is the fusing of two or more lighter atoms into a larger one.
(ii) Fission reaction does not normally occur in nature.
Fusion occurs in stars, such as the Sun.
(iii) For fission, little energy is required.
For fusion, extremely high energy is required.
(iv) For fission, Uranium is the primary fuel used in power plants.
Deuterium and Tritium are the primary fuel used in experimental fusion power plants.
(b) Let us consider the fission of ainto two equal fragments of
nucleus.
Qvalue = (55.93494 – 2 × 27.98191) × 931.5 = – 26.9 MeV
Since, Q is negative. Hence fission is not possible.
Q.7. Define the term wavefront. Using Huygen’s wave theory, verify the law of reflection.
Wavefront:
Wavefront is an imaginary surface over which an optical wave has a constant phase.
Consider a plane wave AB is incident at an angle ‘i’ on a reflecting surface MN.
Let t = time taken by the wave front to advance from B to C with velocity 'v'.
∴ BC = vt
Let CE represent the tangent plane drawn from the point C to the sphere of radius ‘vt’ having A as its center.In ΔAEC and ΔABC,
AE = BC = vt
∠AEC = ∠ABC = 90°
AC = AC (common)
ΔEAC ≌ ΔBAC
Hence ∠i = ∠r
∴ Angle of incidence = angle of reflection.
Q.8. An optical instrument uses an objective lens of power 100 D and an eyepiece of power 40 D. The final image is formed at infinity when the tube length of the instrument is kept at 20 cm.
(a) Identify the optical instrument.
(b) Calculate the angular magnification produced by the instrument.
OR
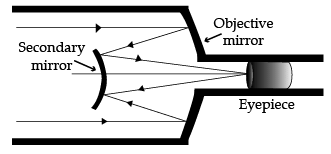
(a) Draw a ray diagram showing the formation of image by a reflecting telescope.
(b) Write two advantages of a reflecting telescope over a refracting telescope.
(a) The instrument is called compound microscope because the focal length of objective lens is smaller than the focal length of eyepiece.
(b) Power of objective = Po = 100 D
∴ f0 = (1/100)m = 1 cm
Power of eyepiece = PE = 40 D
∴ fE = (1/40)m = 2.5 cm
Length of tube = L = 20 cm
D = Least distance of distinct vision (D) = 25 cm
Angular magnification =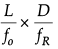
∴ Angular magnification =
OR
(a) Ray Diagram for reflecting telescope.
(b) Two advantages of it over refracting type of telescope.
(i) Ray Diagram
Arrow marking
Labelling
(b) Advantages
(i) Spherical aberration is absent.
(ii) Chromatic aberration is absent.
(iii) Mounting is easier.
(iv) Polishing is done on only one side.
(v) Light gathering power is more.
Q.9. (a) Define the term 'intensity' of radiation in photon picture.
(b) Plot a graph showing the variation of photo current Vs. collector potential for three different intensities I1, I2 and I3 (I1 > I2 > I3), two of which (I1 and I2) have the same frequency n and third has frequency n1 > n.
(c) Explain the nature of the curves on the basis of Einstein's equation.
(a) Intensity of radiation is proportional to (equal to) the number of energy quanta (photons) per unit area per unit time.
Detailed Answer:Intensity: The total energy falling on (or going through) a surface/region per unit area, per unit time and is measured in J/m2 or w/m2 s.
For monochromatic radiation, total energy emitted is equal to the number of photons, n, times the energy of one photon, hn∴ I = hnv/At.
where, A = Area.
t = time.
(b)(c) As per Einstein’s equation
The stopping potential is same for I1 and I2 as they have same frequency.
The saturation currents are as shown, because I1 > I2 > I3
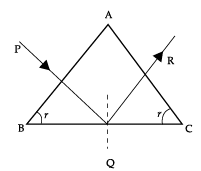
Q.10. A ray of light incident on the face AB of an isosceles triangular prism makes an angle of incidence
(i) and deviates by angle β as shown in the figure. Show that in the position of minimum deviation ∠β = ∠β. Also find out the condition when the refracted ray QR suffers total internal reflection.
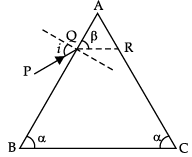
Proving α = β
Finding ic
For minimum deviation, r1 + r2 = A; r1 = r2
(90° − β) + (90° − β) = A
180° − 2β = A
2β = 180° − A
2β = 2α
β = α
r1 + r2 = A
r1 + ic = A
ic = A − r1
ic = A − (90° − β)
Detailed Answer:At the condition of minimum deviation, the refracted ray from surface AB becomes parallel to the base of the prism, thus ΔABC and ΔAQR are similar triangles and hence ∠β = ∠α.
For total internal reflection, the incident ray will have to travel along the normal to the surface AB. So, the ray QR will totally reflected from surface BC.
Q.11. Name the electromagnetic waves with their frequency range, produced in
(a) some radioactive decay
(b) sparks during electric welding
(c) TV remote
OR
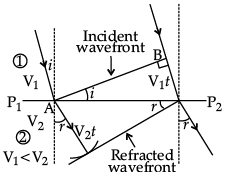
(a) When a wave undergoes reflection at an interface from rarer to denser medium, what is the ad hoc change in its phase ?
(b) Define the term ‘wavefront of light’. A plane wave front AB propagating from denser medium (1) into a rarer medium (2) is incident on the surface P1P2 separating the two media as shown in fig.
Using Huygen’s principle, draw the secondary wavelets and obtain the refracted wavefront in the diagram.
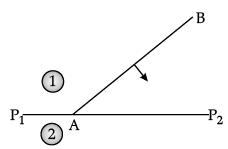
(a) Electromagnetic wave produced in some radioactive decay is γ-rays (frequency > 3 × 1017 Hz).
(b) Electromagnetic wave produced in arc welding are UV (7.5 × 1014 – 3 × 1016 Hz), IR (3 × 1012 – 4.3 × 1014 Hz) and visible (4.3 × 1014 − 7.5 × 1014 Hz) rays.
(c) Electromagnetic wave produced in TV remote is IR rays.
OR
(a) The ad-hoc change in its phase is π.
(b) Wavefront: Wavefront is an imaginary surface over which an optical wave has a constant phase.
Refraction of light from denser medium to rarer medium:
Section - C
Q.12. Case Study : Mirage In Deserts
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object.
Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts.
Based on the above facts, answer the following questions:
(a) Which of the following phenomena is prominently involved in the formation of mirage in deserts?
(i) Refraction and Total Internal Reflection
(ii) Dispersion and Refraction
(iii) Dispersion and scattering of light
(iv) Total internal Reflection and diffraction
(b) A diver at a depth 12 m inside water 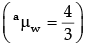 sees the sky in a cone of semi-vertical angle
sees the sky in a cone of semi-vertical angle
(i) sin-1(4/3)
(ii) tan-1(4/3)
(iii) sin-1(3/4)
(iv) 90°
(c) In an optical fibre, if n1 and n2 are the refractive indices of the core and cladding, then which among the following, would be a correct equation?
(i) n1 < n2
(ii) n1 = n2
(iii) n1 << n2
(iv) n1 > n2
(d) A diamond is immersed in such a liquid which has its refractive index with respect to air as greater than the refractive index of water with respect to air. Then the critical angle of diamond liquid interface as compared to critical angle of diamond -water interface will
(i) depend on the nature of the liquid only
(ii) decrease
(iii) remain the same
(iv) increase
(e) The following figure shows a cross-section of a ‘light pipe’ made of a glass fiber of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for the following phenomena to occur.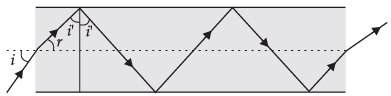
(i) 0 < i < 90°
(ii) 0 < i < 60°
(iii) 0 < i < 45°
(iv) 0 < i < 30°
(a) Option (i) in correct.
Explanation: Mirage in desert is observed due to phenomenon of refraction and Total Internal Reflection.
(b) Option (iii) is correct.
Explanation: aμw = 1/sin C
(c) Option (iv) is correct.
Explanation: The refractive index of the core should be greater than the refractive index of the cladding.
(d) Option (iv) is correct.
Explanation:
μL > μW
Thus C > C'
(e) Option (ii) is correct.
Explanation: 1μ2 = 1/sin C'
Sin C' = 1.44/1.68 = 0.8571
⇒ c' = 59°
Total internal reflection will occur if the angle i' > ic' ,
i.e., if i' > 59° or when r < rmax'
where rmax = 90° – 59° = 31°.
Using Snell’s law,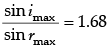
or sin imax = 1.68 × sin rmax
= 1.68 × sin 31°
= 1.68 × 0.5150 = 0.8662
∴ imax = 60°
Thus, all incident rays which make angles in the range 0° < i < 60° with the axis of the pipe will suffer total internal reflection in the pipe.
|
159 docs|4 tests
|