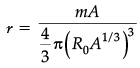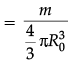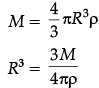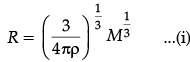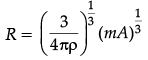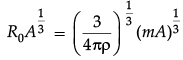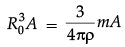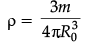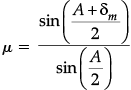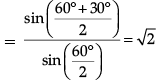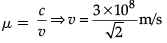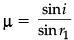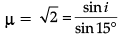Class 12 Physics: CBSE Sample Question Paper- Term II (2021-22)- 3 | Sample Papers for Class 12 Medical and Non-Medical PDF Download
| Table of contents |

|
| Class-XII |

|
| Time: 120 Minutes |

|
| Max. Marks: 35 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-XII
Time: 120 Minutes
Max. Marks: 35
General Instructions :
- There are 12 questions in all. All questions are compulsory.
- This question paper has three sections: Section A, Section B and Section C.
- Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
- There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the choices in such questions.
- You may use log tables if necessary but use of calculator is not allowed.
Section - A
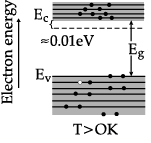
Q.1. In a pure semiconductor crystal of Si, if antimony is added then what type of extrinsic semiconductor is obtained. Draw the energy band diagram of this extrinsic semiconductor so formed.
As given in the statement antimony is added to pure Si crystal, then an n-type extrinsic semiconductor would be so obtained, since antimony(Sb) is a pentavalent impurity.
Energy level diagram of n-type semiconductor:
Q.2. Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but same orbital angular momentum according to the Bohr model? Justify your answer.
OR
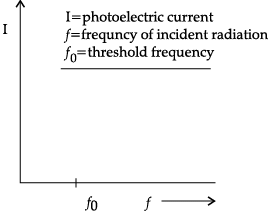
Explain how does (i) photoelectric current and (ii) kinetic energy of the photoelectrons emitted in a photocell vary if the frequency of incident radiation is doubled, but keeping the intensity same?
Show the graphical variation in the above two cases.
No
Because according to Bohr's model, En = (-13.6)/n2 and electrons having different energies belong to different levels having different values of n.
So, similarly their angular momenta will be different, as L = mvr = (nh/2π)
OR
(i) The increase in the frequency of incident radiation has no effect on photoelectric current. This is because of incident photon of increased energy can not eject more than one electron from the metal surface.
(ii) The kinetic energy of the photoelectron becomes more than the double of its original energy. As the work function of the metal is fixed, so incident photon of higher frequency and hence higher energy will impart more energy to the photoelectrons.
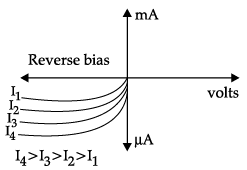
Q.3. Name the device which converts the change in intensity of illumination to change in electric current flowing through it. Plot I-V characteristics of this device for different intensities. State any two applications of this device.
Photodiodes are used to detect optical signals of different intensities by changing current flowing through them.
I-V characteristics of a photodiode
Applications of photodiodes:
- In detection of optical signals
- In demodulation of optical signals
- In light operated switches
- In speed reading of computer punched cards
- In electronic counters (any two out of these or any other relevant application)
Section - B
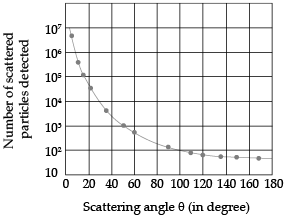
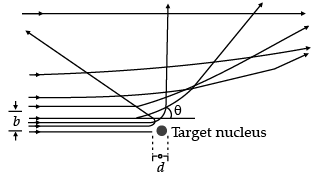
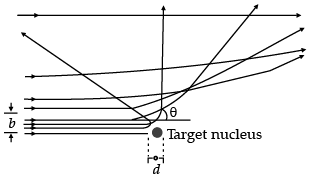
Q.4. Draw a plot of α-particle scattering by a thin foil of gold to show the variation of the number of the scattered particles with scattering angle. Describe briefly how the large angle scattering explains the existence of the nucleus inside the atom. Explain with the help of impact parameter picture, how Rutherford scattering serves a powerful way to determine an upper limit on the size of the nucleus.
Draw a plot of a-particle scattering to show variation of scattering particle.
Describe briefly how large scattering explains existence of nucleus.
Explain with the help of impact parameter picture how Rutherford scattering serves powerful way to determine upper limit of nucleus.The data shows that large number of α-particles do not suffer large scattering but small number suffer greater scattering. It is concluded that
(i) most of the space in the atom is empty.
(ii) massive positively charged nucleus occupies small region.
From the picture, it is clear that small impact parameter suffers large scattering, thus it shows the upper limit to the size of nucleus.
Detailed Answer:
Observation:
- Most of the alpha particles passed through the foil without suffering any collisions.
- Around 0.14% of the incident alpha particles scattered by more than 1°.
- Around 1 in 8000 alpha particles deflected by more than 90°.
Conclusion:
- Since most of the Alpha particles passed through the foil without undergoing any deflection, there must be sufficient empty space within the atom.
- Since few alpha particles were deflected through small angles and alpha particles were positively charged particles, so they could be deflected only by some positive body present within the atom. Those alpha particles deflected which passed very close to this positive body.
- Since some alpha particles were deflected back and alpha particles are heavy particles, so they could be deflected back only when they strike some heavier body inside the atom.
- Since the number of alpha particles deflected back is very-very small, this shows that the heavy body present in an atom must be occupying a small volume.
The small heavy positively charged body present within the atom was called nucleus.
The trajectory, traced by the a-particles in the Coulomb field of target nucleus, has the form as shown below.
The size of the nucleus was estimated by observing the distance (d) of closest approach, of the a-particles. This distance is given by:
where, K = kinetic energy of the a-particles when they are far away from the target nuclei. Since, the value of ‘d’ can easily be calculated or determine when the value of Z is more. Hence, it is more useful for the upper limit on the size of nucleus.
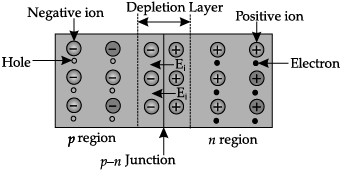
Q.5. Explain the formation of potential barrier and depletion region in a p-n junction diode. What is effect of applying forward bias on the width of depletion region?
Formation of depletion region: In the p-type semiconductor, holes are the majority carrier and in the n-type semiconductor, electrons are the majority carrier.
When a p-n junction is formed, some of the electrons from the n-region which have reached the conduction band are free to diffuse across the junction and combine with holes.
Filling a hole, makes a negative ion in p-side and a positive ion in the n-side. Thus, free charges get depleted and a depletion region is formed, which inhibits any further electron transfer.
Applying forward bias, the depletion region reduces and again electrons can diffuse.
Q.6. Show that the density of nucleus over a wide range of nuclei is constant and independent of mass number.
We have R = R0 A1/3
∴ Density,
Hence r is independent of A.
(Here m is the mass of the nucleus.)Detailed Answer :
Mass of nucleus M = Volume of nucleus × Nuclear density
M = V × p
Let 'R' be the radius of nucleus, then
If m = Mass of one nucleon
M = mA, where A = mass number (Z + N)
Putting the value of M in eq. (i), we get
Since R = R0A1/3
Hence,
Cubing both sides
or,
Hence, nuclear density r, over a wide range of nuclei is constant and independent of mass number A.
Q.7. (a) Compare Maxwell’s electromagnetic theory with Huygens' wave theory of light.
(b) Define incident angle of a light wave.
(a) Both theories treat light as a wave in nature. However, as per Maxwell's electromagnetic theory, light does not need any medium to propagate while for Huygens’ wave theory, a medium is must. That is why, he assumed a hypothetical medium ‘ether’ through which light wave travels in vacuum.
(b) Angle between incident wavefront with the interface is called the incident angle of light wave.
Q.8. (a) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30°. Calculate the speed of light through the prism.
(b) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
OR
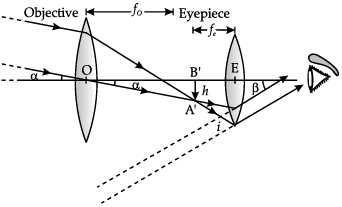
(a) Draw a ray diagram depicting the formation of the image by an astronomical telescope in normal adjustment position. Write the expression for its magnifying power.
(b) You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct an astronomical telescope? Give reason.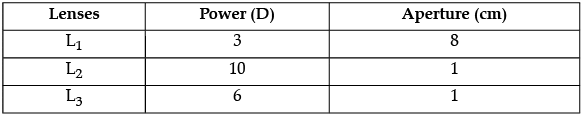
(a) Calculation of speed of light
(b) Calculation of angle of incidence at face AB
(a)
Also
v = 2.122 × 108 m/s
(ii)
At face AC, let the angle of incidence be r2. For grazing ray, e = 90°
Let angle of refraction at face AB be r1.
Now r1 + r2 = A
∴ r1 = A – r2 = 60° – 45° = 15°
Let angle of incidence at this face be i
⇒
∴ i = sin−1(√2 sin15°)
OR
(a) To draw the ray diagram of astronomical telescope
Expression for magnification
Ray diagram:
Magnification = f0/fe
or m = β/α
(b) Since, the objective should have large aperture and large focal length So, lens L1 should be used an objective lens, while the eyepiece should have small aperture and small focal length. So, lens L2 should be used on eye piece.
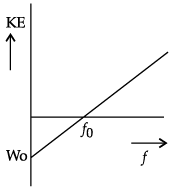
Q.9. Light of same wavelength is incident on three photo-sensitive surfaces A, B and C. The following observations are recorded.
(a) From surface A, photoelectrons are not emitted.
(b) From surface B, photoelectrons are just emitted.
(c) From surface C, photoelectrons with some kinetic energy are emitted.
Compare the threshold frequencies of the three surfaces and justify your answer.
(a) From surface A, electron is not emitted. So, the value of threshold frequency is less than the frequency of the incident radiation.
(b) From surface B, photoelectrons are just emitted. So, the value of threshold frequency is equal to the frequency of the incident radiation.
(c) From surface C, photoelectrons are just emitted with some kinetic energy. So, the value of threshold frequency is more than the frequency of the incident radiation.
Threshold frequency is defined as the minimum frequency of light which causes electron emission from a metal surface.
No electron emission means that the frequency of the light is less than the threshold frequency and electron emission means that the frequency of the light is more than the threshold frequency.
Q.10. Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
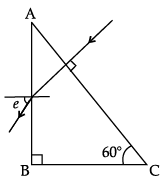
According to Snell's law
μ1sin(i) = μ2sin(r)
μprism = √3 (given)
Refraction at face = AB, ∠i = 30°,
∠r = e (emergent angle)
√3 × sin30° = sine
√3 x (1/2) = sin(e)
Or, e = 60°
Now when the external medium is changed to liquid of μL = 1.3 then,
μprismsin(30) = μLsin(e)
√3 sin(30°) = 1.3sin(e)
e = sin-1= 41.83°
Hence, the angle of emergence angle reduces to 41.83° from 60°.
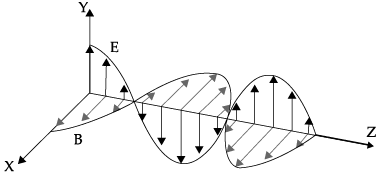
Q.11. (a) How are electromagnetic waves produced ? Depict an electromagnetic wave propagating in Z-direction with its magnetic field  oscillating along X-direction.
oscillating along X-direction.
(b) Write two characteristics of electromagnetic waves.
OR
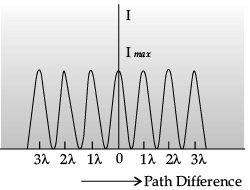
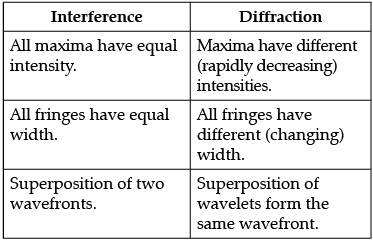
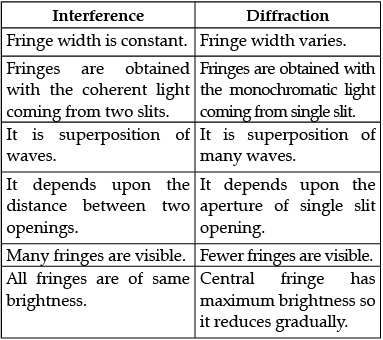
Draw the intensity pattern for single slit diffraction and double slit interference. Hence, state two differences between interference and diffraction patterns.
(a) An electromagnetic wave can be created by accelerating charges or moving charges back and forth.
Electromagnetic wave propagating along the Z-axis:
The magnetic fieldwill be along X-axis.
BX =B0 sin[kz – ωt]The electric field
will be along Y-axis
EY = E0sin[kz–ωt]
(b) Characteristic of electromagnetic waves:
(i) No medium is required for the electromagnetic wave to travel through.
(ii) An electromagnetic wave, although it carries no mass, does carry energy. It also has momentum and can exert pressure (known as radiation pressure).
(iii) The energy carried by an electromagnetic wave is proportional to the frequency of the wave.
OR
Differences:
Detailed Answer:
Intensity Pattern:
Difference between Interference and Diffraction
Section - C
Q.12. Case Study: Sparking Brilliance of Diamond
The total internal reflection of the light is used in polishing diamonds to create a sparking brilliance. By polishing the diamond with specific cuts, it is adjusted the most of the light rays approaching the surface are incident with an angle of incidence more than critical angle. Hence, they suffer multiple reflections and ultimately come out of diamond from the top. This gives the diamond a sparking brilliance.
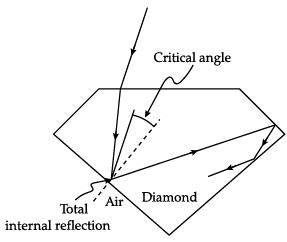
(a) Light cannot easily escape a diamond without multiple internal reflections. This is because:
(i) its critical angle with reference to air is too large.
(ii) its critical angle with reference to air is too small.
(iii) the diamond is transparent.
(iv) rays always enter at angle greater than critical angle.
(b) The critical angle for a diamond is 24.4°. Then its refractive index is:
(i) 2.42
(ii) 0.413
(iii) 1
(iv) 1.413
(c) The basic reason for the extraordinary sparkle of suitably cut diamond is that:
(i) it has low refractive index.
(ii) it has high transparency.
(iii) it has high refractive index.
(iv) it is very hard.
(d) A diamond is immersed in a liquid with a refractive index greater than water. Then the critical angle for total internal reflection will:
(i) depend on the nature of the liquid.
(ii) decrease.
(iii) remains the same.
(iv) increase.
(e) The following diagram shows same diamond cut in two different shapes.
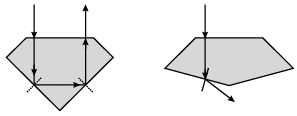
The brilliance of diamond in the second diamond will be:
(i) less than the first.
(ii) greater than first.
(iii) same as first.
(iv) will depend on the intensity of light.
(a) Option (ii) is correct.
Explanation: Since, the refractive index of diamond with respect to air is very small, light gets trapped inside the diamond and hence it sparkles when it comes out of it.
(b) Option (i) is correct.
Explanation: Refractive index = 1/ sin C
C = critical angle = 24.4
∴ μ = 1/sin 24.4 = 1/0.4131 = 2.42
(c) Option (iii) is correct.
Explanation: The brilliance of diamond is due to its too small critical angle with air. As the critical angle become smaller, value of sine of critical angle also become small and hence refractive index increases (since μ = 1/sinC). So, the basic reason for the extraordinary sparkle of suitably cut diamond is its high refractive index.
(d) Option (iv) is correct.
A diamond is immersed in a liquid with a refractive index greater than water. Then the critical angle for total internal reflection will increase.
This is because, as the refractive index of outer medium increases, the refracted ray bends less away from normal. So, angle of incidence should increase more to achieve 90° angle of refraction.
(e) Option (i) is correct.
The brilliance of second diamond will be less than the first since in the second case, no total internal reflection has taken place.
|
159 docs|4 tests
|