Class 11 Physics: CBSE Sample Question Papers- Term II (2021-22)- 1 | Sample Papers for Class 11 Medical and Non-Medical - JEE PDF Download
Class : XI
Time : 120 Minutes
Maximum Marks : 35
General Instructions:
- There are 12 questions in all. All questions are compulsory.
- This question paper has three sections: Section A, Section B and Section C.
- Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
- There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the choices in such questions.
- You may use log tables if necessary but use of calculator is not allowed.
Section - A
Q.1. Derive the equation of continuity.
Equation of continuity. Consider a non-viscous liquid in stream line flow through a tube AB of varying cross-section.
Let a1, a2 = area of cross-sections of the tube at A and B respectively,
v1, v2 = velocities of flow of liquid at A and B respectively.
ρ1, ρ2 = densities of liquid at A and B respectively.
∴ Volume of liquid entering per second at A = a1v1
Mass of liquid entering per second at A = a1v1ρ1
Similarly, mass of liquid leaving per second at B = a2v2ρ2
If there is no loss of liquid in the tube and the flow is steady, then
Mass of liquid entering per second at A
= Mass of liquid leaving per second at B
or a1v1ρ1 = a2v2ρ2 ...(1)
If the liquid is incompressible,
then ρ1 = ρ2
From (1) a1v1 = a2v2
or av = (constant) ...(2)
This is known as equation of continuity.
Q.2. A silica glass rod has a diameter of 1 cm and is 10 cm long. Estimate the largest mass that can be hung from it without breaking it. Breaking strength of glass is 50 × 106 Nm–2.
OR
What are the factors affecting Elasticity?
Using Stress = F/A
we get, F = stress × A
Largest mass = (F/g) =
= 392.7 kg
OR
Factors affecting Elasticity are -
- Hammering and rolling: This result is in an increase in the elasticity of material.
- Annealing: Annealing results in decrease in the elasticity of material.
- Temperature: Elasticity decreases with rise in temperature (Exception: the elasticity of invar steel (alloy) does not change with change in temperature).
- Impurities: This type of effect depends upon the nature of impurities. If the added impurity is more elastic than the substance then its elasticity is increased. If the added impurity is less elastic than the substance, then its elasticity is decreased.
Q.3. What is beam ? What is its use ? Give an expression for the depression of a beam.
Beam is ordinarily a bar supported at its ends.
It is used in the construction of a roof or a bridge.
δ = (Wl)3/4Ybd3
Here, all alphabets are in their usual meanings.
Section - B
Q.4. Estimate the temperature of the surface of the Sun from the following data :
(i) Average radius of the earth’s orbit = 1.5 × 105 km
(ii) Average radius of the Sun = 7.0 × 105 km
(iii) Solar radiant power on the Earth = 1400 Wm–2 at Noon time
Assume the Sun to be a perfect black body will your estimate be greater or less than the actual surface temperature of the Sun ? Explain.
Here, Radius of Sun R = 7 × 105 km
= 7 × 108 m
∴ Surface area of Sun = 4πR2
= 4 π(7 × 108)2
= 6.16 × 1018 m2
σ = 5.67 × 10–8 Wm–2 K–4
Using E = AσT4,
E = (6.16 × 1018) (5.67 × 10–8)T4
= 3.49 × 1011 × T4 W ...(i)
E = 4πr2× Solar radiant power on Earth
Here,
Radius of Earth=r=1.5×105km=1.5×108m
E = 4π(1.5 × 108)2 × 1400
= 3.96 × 1020 watt ...(ii)
Equating eqn (i) and (ii), we get
3.49 × 1011 × T4 = 3.96 × 1020
T = 1.83 × 102 K.
Q.5. For Brownian motion of particles of suspensions in liquid. Answer the following :
(a) What should be the typical size of suspended particles ?
(b) Bombardments of the suspended particles by molecules of the liquid are random. We should then expect equal no. of molecules hitting a suspended particle from all directions. Why is the net impact not zero ?
(c) Can the assembly of suspended particles be considered a ‘gas’ of ‘heavy molecules’ ? If so, what will be the temperature of this gas if temperature of the liquid is T ?
(a) 10–6 m.
(b) The average number of molecules hit in different directions so their net impact is not zero.
(c) Yes, since the heavy gas is in thermal equilibrium with the liquid, its temperature is equal to the temperature of liquid, i.e., T.
Q.6. A truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is 800 N. How much has the cable stretched? (Young’s modulus for steel is 2 × 1011 Nm−2.)
Given:
Steel cable’s length, l = 9.1 m
Radius, r = 5 mm = 5 × 10–3 m.
Tension in cable, F = 800 N
Young’s modulus = 2 × 1011 N/m2
Young’s modulus ,
or
= 4.64 x 10-4m.
Q.7. Calculate (i) r.m.s velocity, and (ii) mean kinetic energy of one gram molecule of hydrogen at S.T.P. (Given, density of hydrogen at S.T.P. is 0.09 kg/m3.)
Here, ρ = 0.09 kg/m3
At S.T.P. P = 1.01 × 105 Pa
(i) According to kinetic theory of gases P = (1/3) ρc2
or
= 1834.8 m/s
(ii) Volume occupied by one mole of hydrogen at S.T.P.
= 22.4 litres
= 22.4 × 10–3 m3
Mass of hydrogen, M = Volume × Density
= 22.4 × 10–3 × 0.09 kg
= 2.016 × 10–3 kg
Mean K.E. of one gram molecule of hydrogen at S.T.P.
= 1/2 M c2
= 1/2 × 2.016 × 10–3 × (1834.8)2
= 3.4 × 103 J
Q.8. A particle is moving in a straight line with S.H.M. of amplitude r. At a distance s from the mean position of motion, the particle receives a blow in the direction of motion which instantaneously doubles the velocity. Find the new amplitude.
OR
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in Fig.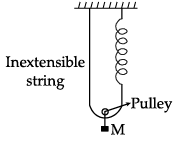
Velocity,
At y = s, let v = v0, then,
v02 = ω2 (r2 – s2) ...(i)
Due to blow, the new velocity at y = s is
v = 2 v0, r = r’
So, (2 v0)2 = ω2 (r’2 – s2) ...(ii)
Dividing (ii) by (i),
On solving
OR
Mg = T + T {system is in equilibrium}
∴ Mg = 2T
because of mass hanging spring elongated by 2l. Where l is the distance moved by hanging mass
T =Fs ( In the spring )
T = 2 kl
∴ Mg= 2 (2kl ) = 2k ( 2l )
displacing mass through y distance downwards Restoring force
F = Mg - 2k (2l + 2y)
= Mg - (2k)(2l) - 4ky
or F = Mg - Mg - 4ky = -4ky
M(d2y/dt2) = -4ky
Q.9. A standing wave is represented by y = 2Asin kx cos ωt. If one of the component waves is y1 = Asin (ωt – kx). What is the equation of the second component wave ?
∴ y = 2Asin kx cos ωt
As 2sin Acos B = sin(A + B) + sin(A – B)
= A sin (kx + ωt) + Asin (kx – ωt)
According to superposition principle, y = y1 + y2
and y1 = Asin (ωt – kx)
= – A sin (kx – ωt)
y2 = y – y1 = 2Asin kx cos ωt + Asin (kx – ωt)
= Asin (kx + ωt) + 2Asin (kx – ωt)
= Asin (kx + ωt) – 2Asin (ωt – kx)
Q.10. A particle moves with S.H.M. in a straight line. In the first second after starting from rest, it travels a distance x1 cm and in the next second it travels a distance x2 cm in the same direction. Prove that the amplitude of oscillation is 
As the particle starts from rest, it must start from the extreme position. Hence, when t = 0, x = r, where r is the required amplitude.
Using the relation, x = rcos ωt
or r – x1 = rcos (ω × 1)
= rcos ω ...(i)
and r – (x1 + x2) = rcos (ω × 2)
Q.11. A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water. The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, maximum intensity of sound is heard. If the room temperature is 20°C, calculate

(a) speed of sound in air at room temperature
(b) speed of sound in air at 0°C
(c) if the water in the tube is replaced with mercury, will there be any difference in your observations?
OR
Show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio 1 : 2 : 3 : 4.
Let us consider the following diagram
For maximum intensity-
(a) L = λ/4
or λ = 4L
v = vλ = v x 4L
= 512 x 4 x 17 x 10-2
= 348.16 m/s
(b) As, v ∝ √T (T = Temperature)
(c) Water and mercury in tube reflects the sound into air column to form stationary wave and reflection is more in mercury than water as mercury is more denser than water. So, intensity of sound heard will be larger but reading does not change as medium in tube (air) and running fork are same.OR
Length for each loop = λ/2
Now, L = nλ/2
λ = 2L/n ...(1)
But v = vλ or λ = v/v
Putting in eqn. (1),
Section - C
Q.12. Case Study : Triple Point:
The temperature of a substance remains constant during its change of state (phase change). A graph between the temperature T and the Pressure P of the substance is called a phase diagram or P-T diagram.
The following figure shows the phase diagram of water and CO2. Such a phase diagram divides the P-T plane into a solid-region, the vapour-region and the liquid-region. The regions are separated by the curves such as sublimation curve (BO), fusion curve (AO) and vaporisation curve (CO).
The points on sublimation curve represent states in which solid and vapour phases coexist. The point on the sublimation curve BO represent states in which the solid and vapour phases coexist.
Points on the fusion curve AO represent states in which solid and liquid phase coexist.
Points on the vaporisation curve CO represent states in which the liquid and vapour phases coexist.
The temperature and pressure at which the fusion curve, the vaporisation curve and the sublimation curve meet and all the three phases of a substance coexist is called the triple point of the substance.
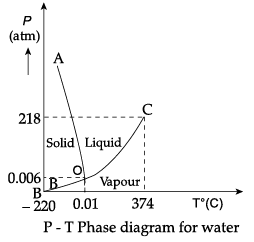
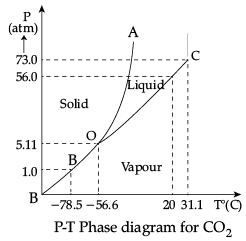
(i) Sublimation curve represents the coexistence of
(a) Solid and liquid state
(b) Solid and vapour state
(c) Liquid and vapour state
(d) Liquid, solid and vapour state
Correct Options is (b)
The points on sublimation curve represent states in which solid and vapour phases coexist. The point on the sublimation curve BO represent states in which the solid and vapour phases coexist.
(ii) The temperature and pressure at which all the three phases of a substance coexist is called
(a) Boiling point
(b) Freezing point
(c) Triple point
(d) Melting point
Correct Options is (c)
The temperature and pressure at which the fusion curve, the vaporisation curve and the sublimation curve meet and all the three phases of a substance coexist is called the triple point of the substance.
(iii) During phase change of a substance
(a) The temperature remains constant
(b) The temperature changes very slowly
(c) The temperature changes very fast
(d) Both temperature and pressure change very slowly
Correct Options is (a)
The temperature of a substance remains constant during its change of state (phase change).
(iv) The triple point of water is:
(a) 0.01°C at 0.006 atmosphere
(b) 0.01K at 0.006 atmosphere
(c) – 0.01K at 0.006 atmosphere
(d) – 0.01°C at 0.006 atmosphere
Correct Options is (a)
From graph, the triple pint of water is 0.01° C at 0.006 atmosphere pressure.
(v) Triple point of CO2 is
(a) – 78.5° C at pressure of 1 atm.
(b) −56.4° C at pressure of 5.11 atm.
(c) −56.4 K at pressure of 5.11 atm.
(d) – 78.5 K at pressure of 1 atm.
Correct Options is (b)
From graph, the triple pint of CO2 is −56.4° C and a pressure of 5.11 atm.
FAQs on Class 11 Physics: CBSE Sample Question Papers- Term II (2021-22)- 1 - Sample Papers for Class 11 Medical and Non-Medical - JEE
| 1. What is the format of the CBSE Class 11 Physics Sample Question Papers for Term II (2021-22)? |  |
| 2. How can I access the CBSE Class 11 Physics Sample Question Papers for Term II (2021-22)? |  |
| 3. What is the purpose of solving the CBSE Class 11 Physics Sample Question Papers for Term II (2021-22)? |  |
| 4. Are the CBSE Class 11 Physics Sample Question Papers for Term II (2021-22) representative of the actual exam? |  |
| 5. Can I use the CBSE Class 11 Physics Sample Question Papers for Term II (2021-22) as a study resource? |  |

|
Explore Courses for JEE exam
|

|



































