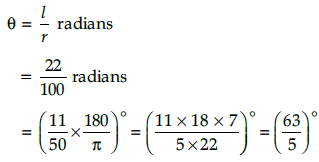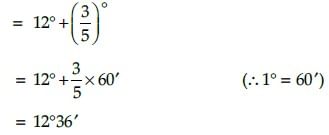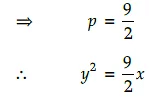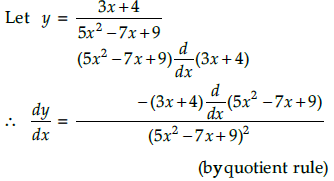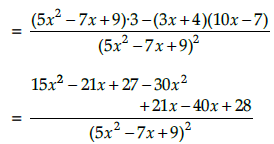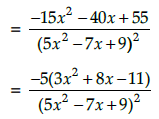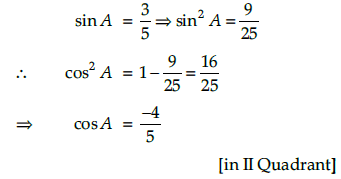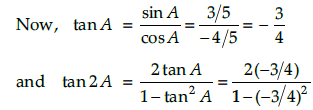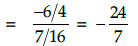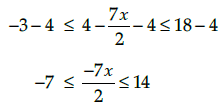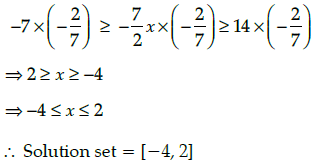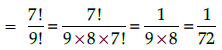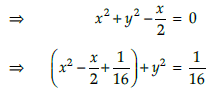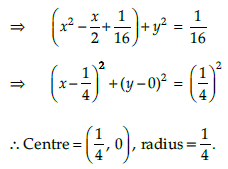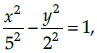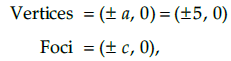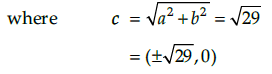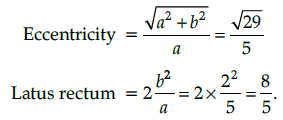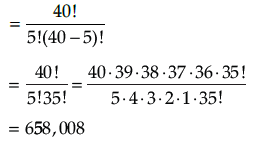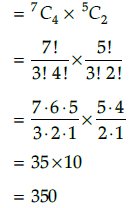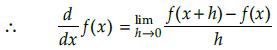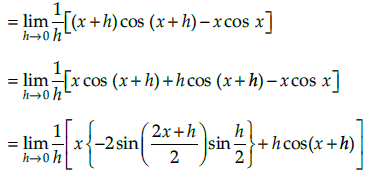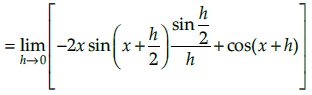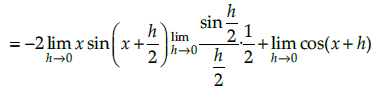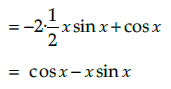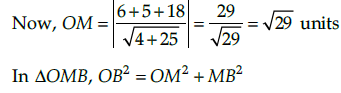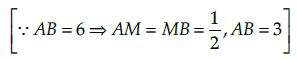Class 11 Math: CBSE Sample Question Papers- Term II (2021-22)- 1 | Sample Papers for Class 11 Medical and Non-Medical - JEE PDF Download
Class XI: Mathematics
Time: 120 Minutes
Max. Marks: 40
General Instructions:
- This question paper contains three sections A, B and C. Each part is compulsory.
- Section - A has 6 short answer type (SA1) questions of 2 marks each.
- Section - B has 4 short answer type (SA2) questions of 3 marks each.
- Section - C has 4 long answer type questions (LA) of 4 marks each.
- There is an internal choice in some of the questions.
- Q14 is a case-based problem having 2 sub parts of 2 marks each.
Section - A
Q.1. A wheel makes 360 revolutions in 1 min. Through how many radians does it turn in 1 second.
No. of revolution in one minute = 360
No. of revolutions in one second =360/60 = 6
∴ 6 revolutions = 6 × 2p = 12p radiansHence, no. of radians turned in one second
= 12p
OR
Find the degree measure of the angle subtended at the centre of circle of radius 100 cm by an arc of length 22 cm (use π =22/7)
Given, l = length of arc = 22 cm
r = radius of circle = 100 cm
Let θ be the angle subtended at the centre,
then
Q.2. If parabola y2 = px passes through point (2, −3), find the length of latus rectum.
Given equation of parabola is y2 = px ...(i)
Since (i) passes through (2, −3).
∴ (-3)2 = p.2
comparing above by y2 =4ax,
a = 9/8
∴ Length of latus rectum = 4a = 9/2 units
Q.3. Differentiate: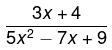
Q.4. If sin A = 3/5 and π/2 < A < π. Find cos A, tan 2A.
Since, sin A > 0 and π/2 < A < π, then A is in II Quadrant.
Q.5. Solve the inequality: 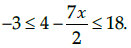
The given inequality
Adding (−4) to each term,
Multiplying by (-2/7) to each term
Q.6. If the letters of the word ‘ALGORITHM’ are arranged at random in a row what is the probability the letter ‘GOR’ must remain together as a unit ?
Number of letters in the word ‘ALGORITHM’ is 9
If ‘GOR’ remain together, then considered it as 1 number
∴ Number of letters = 6 + 1 = 7
Number of words, if ‘GOR’ remain together = 7!
Total number of words from the letters of the word ‘ALGORITHM’ = 9!
∴ Required probability
OR
A card is selected from a pack of 52 cards.
(i) What is the sample space?
(ii) Calculate the probability that card is an ace of spade?
(i) Sample space i.e. n(S) = 52
(ii) Number of ace of spade in a pack = 1 i.e. n(E) = 1
Probability that card is an ace = n(E)/n(S) = 1/52.
Section - B
Q.7. Find the centre and radius of the circle 2x2 + 2y2 – x = 0.
Given equation of the circle is
2x2 + 2y2 – x = 0
Q.8. Find the co-ordinate of the vertices, foci eccentricity and length of latus rectum of the hyperbola.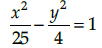
OR
Find the distance between the directrices of the hyperbola x2 – y2 = 8.
The given hyperbola
here a = 5, b = 2
Q.9. From a class of 40 students, in how many ways can five students be chosen for an excursion party.
From a class of 40 students, five students can be chosen for an excursion party in 40C5 ways
Q.10. From a group of 7 boys and 5 girls, a team consisting of 4 boys and 2 girls is to be made. In how many different ways it can be done?
From a group of 7 boys, 4 boys can be choose in 7C4 ways.
From a group of 5 girls, 2 girls can be choose in 5C2 ways.
∴ Required number of ways to choose a team consisting 4 boys and 2 girls are
Section - C
Q.11. Using first principle find the derivative of x cos x function
Let f (x) = x cos x
∴ f(x+h) = (x+h) cos (x+h)
Q.12. Find the equation of a circle passing through the point (7, 3) having radius 3 units and whose centre lies on the line y = x – 1.
Let equation of circle be
(x-h)2+(y-k)2 = r2
⇒ (x-h)2 + (y-k)2 = 9 ...(i)
Now, the circle passes through the point (7, 3)(7-h)2 + (3-k)3 = 9 ... (ii)
⇒ 49 - 14h + h2 + 9 - 6k + k2=9
⇒ h2+k2-14h-6k+49 = 0 ....(iii)
Now, y=x-1, k=h-1
on putting k=h-1 in Eq. (iii), we get
h2+(h-1)2 - 14h - 6(h-1)+49 = 0
⇒ h2+h2-2h+1 - 14h - 6h + 6+49 = 0
⇒ 2h2-22h+56=0
⇒ h2-11h+28 =0
⇒ h2-7h-4h+28=0
⇒ h(h-7)-4(h-7)=0
⇒ (h-7)(h-4)=0
∴ h=4,7
When h = 7 then k = 7 – 1 = 6
∴ Centre (7, 6)
When h = 4 then k = 3
∴ Centre = (4, 3)
So, the equation of circle when centre (7, 6), is
(x-7)2 + (y-6)2 = 9⇒ x2-14x+49+y2-12y+36 =9
⇒ x2+y2-14x-12y+76 = 0
when centre (4, 3), then the equation of circle is,
(x-4)2 + (y-3)2 = 9
⇒ x2-8x+16+y2-6y+9 =9
⇒ x2+y-8x-6y+16 =0
OR
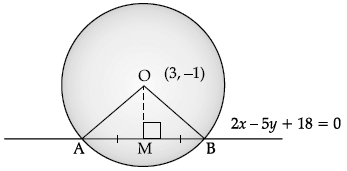
Find the equation of a circle whose centre is (3, –1) and which cuts off a chord length 6 units on the line 2x – 5y + 18 = 0.
Given, centre of the circle is (3, –1),
⇒ OB2 = 29+9
⇒ OB2= 38 units
So, the radius of circle is √38, units
∴ Equation of the circle with radius
r = √38 units and centre (3, –1) is⇒ (x-3)2 + (y+1)2 = 38
⇒ x2-6x+9+y2+2y+1=38
x2+y2-6x+2y=28
x2+y2-6x+2y-28=0
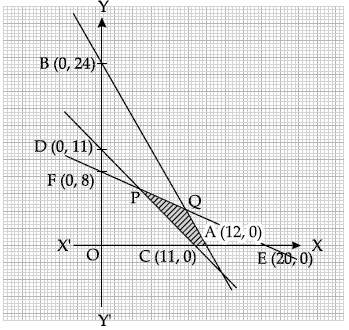
Q.13. Solve the following system of inequalities graphically
2x + y ≤ 24,
x + y ≥ 11,
2x + 5y ≤ 40, x, y ≥ 0.
Inequality (x ≥ 0) represents the region on the right of Y-axis and Y-axis itself. Inequality (y ≥ 0) represents the region above X-axis and X-axis itself.
2x + y ≤ 24 ...(i)
x + y ≥ 11 ...(ii)
2x + 5y ≤ 40, x, y ≥ 0 ...(iii)
We first draw the graph of lines
2x + y = 24, x + y = 11 and 2x + 5y = 40
Now, 2x + y = 24, passes through A(12, 0) and B(0, 24)Again, x + y = 11, passes through C(11, 0) and D(0, 11)
Further 2x + 5y = 40, passes through E(20, 0) and F(0, 8)
Shaded area PQAC is the solution area.
Case-Based/Data Based
Q.14. A child's game has 8 triangles of which 3 are blue and rest are red, and 10 squares of which 6 are blue and rest are red. One piece is lost at random.
(i) Find the probability that lost piece is triangle.
(i) Since, total no. of triangles = 8
Triangles with blue colour = 3
Triangles with red colour = 8 – 3 = 5
and total no. of squares = 10
Squares with blue colour = 6
Squares with red colour = 10 – 6 = 4
Number of favourable outcomes for the event that lost figure is triangle, i.e., F (E) = 8
Total figures (square and triangle)= 8 + 10 = 18
i.e., T(E) = 18
Probability (getting a triangle),
P(E) = F(E)/T(E)
= 8/18 = 4/9
(ii) Find the probabilities that lost piece is square of blue colour & triangle of red colour.
(ii) Number of favourable outcomes for the events that lost figure is square of blue colour, i.e., F(E) = 6 and T(E) = 18
∴ P(getting a blue square),
P(E) = F(E)/T(E)
= 6/18 = 1/3Number of favourable outcomes for the event that lost figure is triangle of red colour = 5,
i.e., F(E) = 5 and
T(E) = 18∴ P(lost figure is red triangle),
P(E) = 5/18