Lab Manual: Quadratic Polynomials - Class 9 PDF Download

Clear all your Class 9 doubts with EduRev Join for Free

Join for Free

Objective

• x² + 5x + 6
• x² – 5x + 6

Prerequisite Knowledge

• Knowledge of quadratic equations.
• Splitting of the middle term of a quadratic polynomial as ax² + bx + c = a(x + p)(x – q) where
  
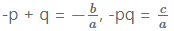
• Area of a rectangle = l x b
• Area of a square = (side)² 

Materials Required
Glazed papers (blue, green, orange, yellow and pink), white sheet of paper, geometry box, ruler, pair of scissors and gluestick.

Procedure

• Every x² represents the area of pink square of side x-units.
  Therefore, to represent 2x², use two pink squares of side x units each. Take x as 3 units.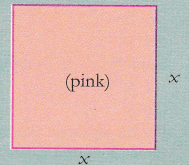
  
• Every x represents area of a green rectangular strip of dimensions (1 x x).
  [For 5x, use 5 green strips each of dimensions (1 x x)]
  
• Every (-x) is represented by a blue rectangular strip of dimensions (1 x x).
  For (-5x), use 5 blue strips each of dimensions (1 x x).
  
• All positive integers are represented by yellow unit squares and all negative integers are shown by orange squares.
  

Case I
Let us consider the expression x² + 5x + 6 which is of the form (ax² + bx + 2).

• The polynomial x² + 5x + 6
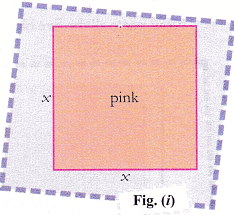
  ⇒ x² + 3x + 2x + 6 can be factorized as (x + 3)(x + 2).
• To present x², draw a pink square of xunits [fig. (i)].
  
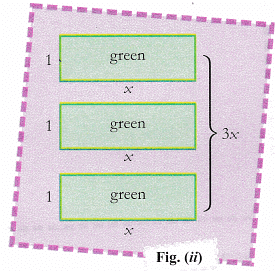
• To represent 3x, draw three rectangular strips of green colour of dimension (1 x x) [fig. (ii)].
  
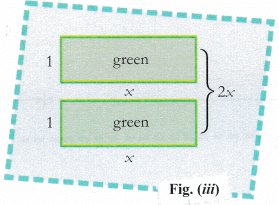
• To represent 2x, draw two green rectangular strips of dimensions (1 x x) [fig. (iii)].
  
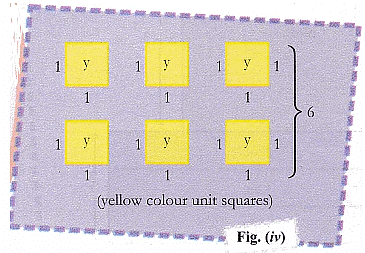
• To represent 6, draw 6 yellow unit squares [fig. (iv)].
  
• Cut all the strips from the glazed paper.
• Now, paste all the strips together on the white sheet of paper as shown in fig.(v).
  
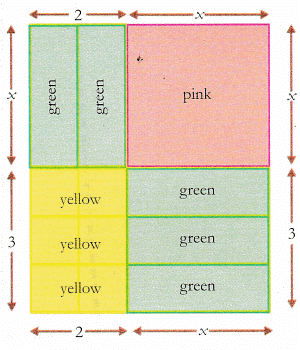  Fig. (v)

Case II
Consider the expression x² – 5x + 6 and factorize it x² – 3x – 2x + 6 = (x – 3)(x – 2).

• Cut a pink square of dimension xunits (say 8 units).
• To represent 6, cut six yellow squares of dimension 1 unit.
• To represent -5x {(-3x) + (-2x)}, cut five blue strips of dimension (1 x x).
• Paste the pink square strips and all the yellow squares on a white sheet paper as shown in fig. (vi).
  
  Fig. (vi)
• Now, paste all the five blue strips over the pink polygon as shown in fig. (vii).
  
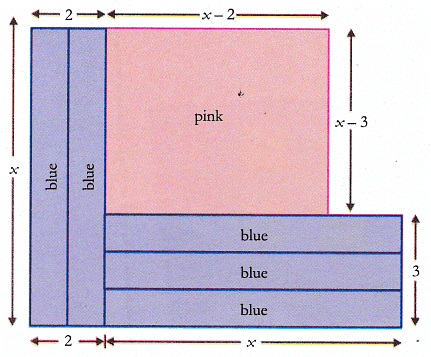  Fig. (vii)

Observation and Calculation
Case I
x² + 5x + 6
area of 5 green strips = 5x = 2x + 3x
area of pink square = x²
area of 6 yellow unit squares = 6
total area of rectangle obtained = x² + 3x + 2x + 6 = x² + 5x + 6 = (x + 3)(x + 2)

Case II
x² – 5x + 6
area of 5 blue rectangular strips = 5x (negative)
area of a pink square = x²
area of 6 yellow unit squares = 6

total area of pink rectangle obtained after pasting all strips
= (x – 2)(x – 3)
= x² – 2x – 3x + 6
= x² – 5x + 6x
∴ x² – 5x + 6 = (x – 3)(x – 2)

Result
We verified the factors of two quadratic polynomials geometrically by paper cutting and pasting.

Learning Outcome
Above method gives us the geometrical interpretation of the factorization of quadratic expressions of the form ax² + bx + c or ax² – bx + c.

Remarks

• Pasting of blue strips over pink area means reducing pink area.
• The pink portion so obtained represents the factors of the given quadratic expression.
• Students may take different colour combinations.

Activity Time
By using paper cutting and pasting method, represent the factors of following quadratic expressions:

• x² – x – 6
• 2x² + 5x + 2