Open App

Class 8 Exam > Class 8 Notes > The Stock Span Problem

The Stock Span Problem - Class 8 PDF Download

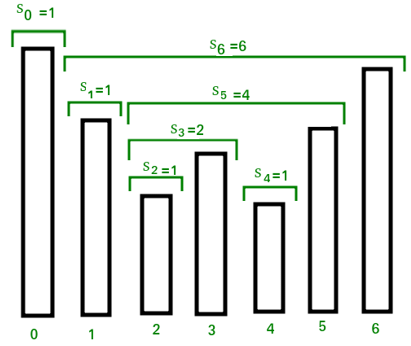
The stock span problem is a financial problem where we have a series of n daily price quotes for a stock and we need to calculate the span of stock’s price for all n days. The span Si of the stock’s price on a given day i is defined as the maximum number of consecutive days just before the given day, for which the price of the stock on the current day is less than its price on the given day.
For example:

Input: N = 7, price[] = [100 80 60 70 60 75 85]
Output: 1 1 1 2 1 4 6
Explanation: Traversing the given input span for 100 will be 1, 80 is smaller than 100 so the span is 1, 60 is smaller than 80 so the span is 1, 70 is greater than 60 so the span is 2 and so on. Hence the output will be 1 1 1 2 1 4 6.

Input: N = 6, price[] = [10 4 5 90 120 80]
Output:1 1 2 4 5 1
Explanation: Traversing the given input span for 10 will be 1, 4 is smaller than 10 so the span will be 1, 5 is greater than 4 so the span will be 2 and so on. Hence, the output will be 1 1 2 4 5 1.

The Stock Span Problem - Class 8

A Simple but inefficient method
Traverse the input price array. For every element being visited, traverse elements on the left of it and increment the span value of it while elements on the left side are smaller.
Following is the implementation of this method:

C++

// C++ program for brute force method
// to calculate stock span values
#include <bits/stdc++.h>
using namespace std;

// Fills array S[] with span values
void calculateSpan(int price[], int n, int S[])
{
// Span value of first day is always 1
S[0] = 1;

// Calculate span value of remaining days
// by linearly checking previous days
for (int i = 1; i < n; i++)
{
S[i] = 1; // Initialize span value

// Traverse left while the next element
// on left is smaller than price[i]
for (int j = i - 1; (j >= 0) &&
(price[i] >= price[j]); j--)
S[i]++;
}
}

// A utility function to print elements of array
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}

// Driver code
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S, n);

return 0;
}

// This is code is contributed by rathbhupendra

C

// C program for brute force method to calculate stock span values
#include <stdio.h>

// Fills array S[] with span values
void calculateSpan(int price[], int n, int S[])
{
// Span value of first day is always 1
S[0] = 1;

// Calculate span value of remaining days by linearly checking
// previous days
for (int i = 1; i < n; i++) {
S[i] = 1; // Initialize span value

// Traverse left while the next element on left is smaller
// than price[i]
for (int j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}

// A utility function to print elements of array
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
}

// Driver program to test above function
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S, n);

return 0;
}

Java

// Java implementation for brute force method to calculate stock span values

import java.util.Arrays;

class GFG {
// method to calculate stock span values
static void calculateSpan(int price[], int n, int S[])
{
// Span value of first day is always 1
S[0] = 1;

// Calculate span value of remaining days by linearly checking
// previous days
for (int i = 1; i < n; i++) {
S[i] = 1; // Initialize span value

// Traverse left while the next element on left is smaller
// than price[i]
for (int j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}

// A utility function to print elements of array
static void printArray(int arr[])
{
System.out.print(Arrays.toString(arr));
}

// Driver program to test above functions
public static void main(String[] args)
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = price.length;
int S[] = new int[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S);
}
}
// This code is contributed by Sumit Ghosh

Python3

# Python program for brute force method to calculate stock span values

# Fills list S[] with span values
def calculateSpan(price, n, S):

# Span value of first day is always 1
S[0] = 1

# Calculate span value of remaining days by linearly
# checking previous days
for i in range(1, n, 1):
S[i] = 1 # Initialize span value

# Traverse left while the next element on left is
# smaller than price[i]
j = i - 1
while (j>= 0) and (price[i] >= price[j]) :
S[i] += 1
j -= 1

# A utility function to print elements of array
def printArray(arr, n):

for i in range(n):
print(arr[i], end = " ")

# Driver program to test above function
price = [10, 4, 5, 90, 120, 80]
n = len(price)
S = [None] * n

# Fill the span values in list S[]
calculateSpan(price, n, S)

# print the calculated span values
printArray(S, n)

# This code is contributed by Sunny Karira

C#

// C# implementation for brute force method
// to calculate stock span values
using System;

class GFG {

// method to calculate stock span values
static void calculateSpan(int[] price,
int n, int[] S)
{

// Span value of first day is always 1
S[0] = 1;

// Calculate span value of remaining
// days by linearly checking previous
// days
for (int i = 1; i < n; i++) {
S[i] = 1; // Initialize span value

// Traverse left while the next
// element on left is smaller
// than price[i]
for (int j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}

// A utility function to print elements
// of array
static void printArray(int[] arr)
{
string result = string.Join(" ", arr);
Console.WriteLine(result);
}

// Driver function
public static void Main()
{
int[] price = { 10, 4, 5, 90, 120, 80 };
int n = price.Length;
int[] S = new int[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S);
}
}

// This code is contributed by Sam007.

PHP

<?php
// PHP program for brute force method
// to calculate stock span values

// Fills array S[] with span values
function calculateSpan($price, $n, $S)
{

// Span value of first
// day is always 1
$S[0] = 1;

// Calculate span value of
// remaining days by linearly
// checking previous days
for ($i = 1; $i < $n; $i++)
{

// Initialize span value
$S[$i] = 1;

// Traverse left while the next
// element on left is smaller
// than price[i]
for ($j = $i - 1; ($j >= 0) &&
($price[$i] >= $price[$j]); $j--)
$S[$i]++;
}

// print the calculated
// span values
for ($i = 0; $i < $n; $i++)
echo $S[$i] . " ";;

}

// Driver Code
$price = array(10, 4, 5, 90, 120, 80);
$n = count($price);
$S = array($n);

// Fill the span values in array S[]
calculateSpan($price, $n, $S);

// This code is contributed by Sam007
?>

Javascript

<script>
// Javascript implementation for brute force method
// to calculate stock span values

// method to calculate stock span values
function calculateSpan(price, n, S)
{

// Span value of first day is always 1
S[0] = 1;

// Calculate span value of remaining
// days by linearly checking previous
// days
for (let i = 1; i < n; i++) {
S[i] = 1; // Initialize span value

// Traverse left while the next
// element on left is smaller
// than price[i]
for (let j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}

// A utility function to print elements
// of array
function printArray(arr)
{
let result = arr.join(" ");
document.write(result);
}

let price = [ 10, 4, 5, 90, 120, 80 ];
let n = price.length;
let S = new Array(n);
S.fill(0);

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S);

</script>

Output

1 1 2 4 5 1

The Time Complexity of the above method is O(n^2). We can calculate stock span values in O(n) time.
A Linear-Time Complexity Method

We see that S[i] on the day i can be easily computed if we know the closest day preceding i, such that the price is greater than on that day than the price on the day i.
If such a day exists, let’s call it h(i), otherwise, we define h(i) = -1.
The span is now computed as S[i] = i – h(i). See the following diagram.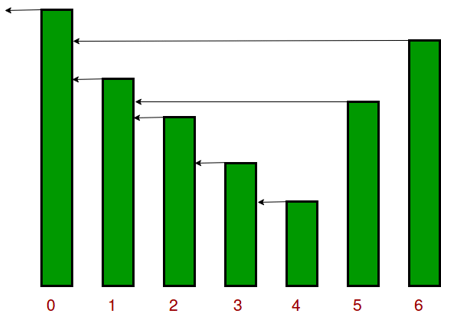
The Stock Span Problem - Class 8

To implement this logic, we use a stack as an abstract data type to store the days i, h(i), h(h(i)), and so on. When we go from day i-1 to i, we pop the days when the price of the stock was less than or equal to price[i] and then push the value of day i back into the stack.
Following is the implementation of this method.
We have to check also for a case when all the stock prices should be the same so therefore we have to just check whether the current stock price is bigger than the previous one or not. We will not pop from the stack when the current and previous stock prices are the same.

C++

// C++ linear time solution for stock span problem
#include <iostream>
#include <stack>
using namespace std;

// A stack based efficient method to calculate
// stock span values
void calculateSpan(int price[], int n, int S[])
{
// Create a stack and push index of first
// element to it
stack<int> st;
st.push(0);

// Span value of first element is always 1
S[0] = 1;

// Calculate span values for rest of the elements
for (int i = 1; i < n; i++) {
// Pop elements from stack while stack is not
// empty and top of stack is smaller than
// price[i]
while (!st.empty() && price[st.top()] <= price[i])
st.pop();

// If stack becomes empty, then price[i] is
// greater than all elements on left of it,
// i.e., price[0], price[1], ..price[i-1]. Else
// price[i] is greater than elements after
// top of stack
S[i] = (st.empty()) ? (i + 1) : (i - st.top());

// Push this element to stack
st.push(i);
}
}

// A utility function to print elements of array
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}

// Driver program to test above function
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S, n);

return 0;
}

Java

// Java linear time solution for stock span problem

import java.util.Stack;
import java.util.Arrays;

public class GFG {
// A stack based efficient method to calculate
// stock span values
static void calculateSpan(int price[], int n, int S[])
{
// Create a stack and push index of first element
// to it
Stack<Integer> st = new Stack<>();
st.push(0);

// Span value of first element is always 1
S[0] = 1;

// Calculate span values for rest of the elements
for (int i = 1; i < n; i++) {

// Pop elements from stack while stack is not
// empty and top of stack is smaller than
// price[i]
while (!st.empty() && price[st.peek()] <= price[i])
st.pop();

// If stack becomes empty, then price[i] is
// greater than all elements on left of it, i.e.,
// price[0], price[1], ..price[i-1]. Else price[i]
// is greater than elements after top of stack
S[i] = (st.empty()) ? (i + 1) : (i - st.peek());

// Push this element to stack
st.push(i);
}
}

// A utility function to print elements of array
static void printArray(int arr[])
{
System.out.print(Arrays.toString(arr));
}

// Driver method
public static void main(String[] args)
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = price.length;
int S[] = new int[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S);
}
}
// This code is contributed by Sumit Ghosh

Python3

# Python linear time solution for stock span problem

# A stack based efficient method to calculate s
def calculateSpan(price, S):

n = len(price)
# Create a stack and push index of first element to it
st = []
st.append(0)

# Span value of first element is always 1
S[0] = 1

# Calculate span values for rest of the elements
for i in range(1, n):

# Pop elements from stack while stack is not
# empty and top of stack is smaller than price[i]
while( len(st) > 0 and price[st[-1]] <= price[i]):
st.pop()

# If stack becomes empty, then price[i] is greater
# than all elements on left of it, i.e. price[0],
# price[1], ..price[i-1]. Else the price[i] is
# greater than elements after top of stack
S[i] = i + 1 if len(st) <= 0 else (i - st[-1])

# Push this element to stack
st.append(i)

# A utility function to print elements of array
def printArray(arr, n):
for i in range(0, n):
print (arr[i], end =" ")

# Driver program to test above function
price = [10, 4, 5, 90, 120, 80]
S = [0 for i in range(len(price)+1)]

# Fill the span values in array S[]
calculateSpan(price, S)

# Print the calculated span values
printArray(S, len(price))

# This code is contributed by Nikhil Kumar Singh (nickzuck_007)

C#

// C# linear time solution for
// stock span problem
using System;
using System.Collections;

class GFG {
// a linear time solution for
// stock span problem A stack
// based efficient method to calculate
// stock span values
static void calculateSpan(int[] price, int n, int[] S)
{
// Create a stack and Push
// index of first element to it
Stack st = new Stack();
st.Push(0);

// Span value of first
// element is always 1
S[0] = 1;

// Calculate span values
// for rest of the elements
for (int i = 1; i < n; i++) {

// Pop elements from stack
// while stack is not empty
// and top of stack is smaller
// than price[i]
while (st.Count > 0 && price[(int)st.Peek()] <= price[i])
st.Pop();

// If stack becomes empty, then price[i] is
// greater than all elements on left of it, i.e.,
// price[0], price[1], ..price[i-1]. Else price[i]
// is greater than elements after top of stack
S[i] = (st.Count == 0) ? (i + 1) : (i - (int)st.Peek());

// Push this element to stack
st.Push(i);
}
}

// A utility function to print elements of array
static void printArray(int[] arr)
{
for (int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
}

// Driver method
public static void Main(String[] args)
{
int[] price = { 10, 4, 5, 90, 120, 80 };
int n = price.Length;
int[] S = new int[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S);
}
}

// This code is contributed by Arnab Kundu

Javascript

<script>
// javascript linear time solution for stock span problem

// A stack based efficient method to calculate
// stock span values
function calculateSpan(price , n , S)
{

// Create a stack and push index of first element
// to it
var st = [];
st.push(0);

// Span value of first element is always 1
S[0] = 1;

// Calculate span values for rest of the elements
for (var i = 1; i < n; i++) {

// Pop elements from stack while stack is not
// empty and top of stack is smaller than
// price[i]
while (st.length!==0 && price[st[st.length - 1]] <= price[i])
st.pop();

// If stack becomes empty, then price[i] is
// greater than all elements on left of it, i.e.,
// price[0], price[1], ..price[i-1]. Else price[i]
// is greater than elements after top of stack
S[i] = (st.length===0) ? (i + 1) : (i - st[st.length - 1]);

// Push this element to stack
st.push(i);
}
}

// A utility function to print elements of array
function printArray(arr) {
document.write(arr);
}

// Driver method

var price = [ 10, 4, 5, 90, 120, 80 ];
var n = price.length;
var S = Array(n).fill(0);

// Fill the span values in array S
calculateSpan(price, n, S);

// print the calculated span values
printArray(S);

// This code contributed by Rajput-Ji
</script>

Output

1 1 2 4 5 1

Time Complexity: O(n). It seems more than O(n) at first look. If we take a closer look, we can observe that every element of the array is added and removed from the stack at most once. So there are total 2n operations at most. Assuming that a stack operation takes O(1) time, we can say that the time complexity is O(n).
Auxiliary Space: O(n) in the worst case when all elements are sorted in decreasing order.
Another approach: (without using stack)

C++

// C++ program for a linear time solution for stock
// span problem without using stack
#include <iostream>
#include <stack>
using namespace std;

// An efficient method to calculate stock span values
// implementing the same idea without using stack
void calculateSpan(int A[], int n, int ans[])
{
// Span value of first element is always 1
ans[0] = 1;

// Calculate span values for rest of the elements
for (int i = 1; i < n; i++) {
int counter = 1;
while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}

// A utility function to print elements of array
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}

// Driver program to test above function
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S, n);

return 0;
}

Java

// Java program for a linear time
// solution for stock span problem
// without using stack
class GFG {

// An efficient method to calculate
// stock span values implementing the
// same idea without using stack
static void calculateSpan(int A[],
int n, int ans[])
{
// Span value of first element is always 1
ans[0] = 1;

// Calculate span values for rest of the elements
for (int i = 1; i < n; i++) {
int counter = 1;
while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}

// A utility function to print elements of array
static void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}

// Driver code
public static void main(String[] args)
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = price.length;
int S[] = new int[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S, n);
}
}

/* This code contributed by PrinciRaj1992 */

Python3

# Python3 program for a linear time
# solution for stock span problem
# without using stack

# An efficient method to calculate
# stock span values implementing
# the same idea without using stack
def calculateSpan(A, n, ans):

# Span value of first element
# is always 1
ans[0] = 1

# Calculate span values for rest
# of the elements
for i in range(1, n):
counter = 1

while ((i - counter) >= 0 and
A[i] >= A[i - counter]):
counter += ans[i - counter]
ans[i] = counter

# A utility function to print elements
# of array
def printArray(arr, n):

for i in range(n):
print(arr[i], end = ' ')
print()

# Driver code
price = [ 10, 4, 5, 90, 120, 80 ]
n = len(price)
S = [0] * (n)

# Fill the span values in array S[]
calculateSpan(price, n, S)

# Print the calculated span values
printArray(S, n)

# This code is contributed by Prateek Gupta

C#

// C# program for a linear time
// solution for stock span problem
// without using stack
using System;
public class GFG {

// An efficient method to calculate
// stock span values implementing the
// same idea without using stack
static void calculateSpan(int[] A,
int n, int[] ans)
{
// Span value of first element is always 1
ans[0] = 1;

// Calculate span values for rest of the elements
for (int i = 1; i < n; i++) {
int counter = 1;
while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}

// A utility function to print elements of array
static void printArray(int[] arr, int n)
{
for (int i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}

// Driver code
public static void Main(String[] args)
{
int[] price = { 10, 4, 5, 90, 120, 80 };
int n = price.Length;
int[] S = new int[n];

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S, n);
}
}
// This code has been contributed by 29AjayKumar

JavaScript

<script>

// JavaScript program for the above approach;

// An efficient method to calculate stock span values
// implementing the same idea without using stack
function calculateSpan(A, n, ans)
{

// Span value of first element is always 1
ans[0] = 1;

// Calculate span values for rest of the elements
for (let i = 1; i < n; i++) {
let counter = 1;
while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}

// A utility function to print elements of array
function printArray(arr, n) {
for (let i = 0; i < n; i++)
document.write(arr[i] + " ");
}

// Driver program to test above function
let price = [10, 4, 5, 90, 120, 80];
let n = price.length;
let S = new Array(n);

// Fill the span values in array S[]
calculateSpan(price, n, S);

// print the calculated span values
printArray(S, n);

// This code is contributed by Potta Lokesh
</script>

Output

1 1 2 4 5 1

A Stack Based approach:

In this approach, I have used the data structure stack to implement this task.
Here, two stacks are used. One stack stores the actual stock prices whereas, the other stack is a temporary stack.
The stock span problem is solved using only the Push and Pop functions of Stack.
Just to take input values, I have taken array ‘price’ and to store output, used array ‘span’.

Below is the implementation of the above approach:

C

// C program for the above approach
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
#define SIZE 6

// change size of stack from here
// change this char to int if
// you want to create stack of
// int. rest all program will work fine
typedef int stackentry;

typedef struct stack {
stackentry entry[SIZE];
int top;
} STACK;

// stack is initialized by setting top pointer = -1.
void initialiseStack(STACK* s) { s->top = -1; }

// to check if stack is full.
int IsStackfull(STACK s)
{
if (s.top == SIZE - 1) {
return (1);
}
return (0);
}

// to check if stack is empty.
int IsStackempty(STACK s)
{
if (s.top == -1) {
return (1);
}
else {
return (0);
}
}

// to push elements into the stack.
void push(stackentry d, STACK* s)
{
if (!IsStackfull(*s)) {

s->entry[(s->top) + 1] = d;
s->top = s->top + 1;
}
}

// to pop element from stack.
stackentry pop(STACK* s)
{
stackentry ans;
if (!IsStackempty(*s)) {
ans = s->entry[s->top];
s->top = s->top - 1;
}
else {

// '\0' will be returned if
// stack is empty and of
// char type.
if (sizeof(stackentry) == 1)
ans = '\0';
else
// INT_MIN will be returned
// if stack is empty
// and of int type.
ans = INT_MIN;
}
return (ans);
}

// The code for implementing stock
// span problem is written
// here in main function.
int main()
{
// Just to store prices on 7 adjacent days
int price[6] = { 10, 4, 5, 90, 120, 80 };

// in span array , span of each day will be stored.
int span[6] = { 0 };
int i;

// stack 's' will store stock values of each
// day. stack 'temp' is temporary stack
STACK s, temp;

// setting top pointer to -1.
initialiseStack(&s);
initialiseStack(&temp);

// count basically signifies span of
// particular day.
int count = 1;

// since first day span is 1 only.
span[0] = 1;
push(price[0], &s);

// calculate span of remaining days.
for (i = 1; i < 6; i++) {

// count will be span of that particular day.
count = 1;

// if current day stock is larger than previous day
// span, then it will be popped out into temp stack.
// popping will be carried out till span gets over
// and count will be incremented .

while (!IsStackempty(s)
&& s.entry[s.top] <= price[i]) {
push(pop(&s), &temp);
count++;
}

// now, one by one all stocks from temp will be
// popped and pushed back to s.
while (!IsStackempty(temp)) {
push(pop(&temp), &s);
}

// pushing current stock
push(price[i], &s);

// appending span of that particular
// day into output array.
span[i] = count;
}

// printing the output.
for (i = 0; i < 6; i++)
printf("%d ", span[i]);
}

Output

1 1 2 4 5 1

The document The Stock Span Problem - Class 8 is a part of Class 8 category.

All you need of Class 8 at this link: Class 8

About this Document

Sep 09, 2025 Last updated

Related Exams

Class 8

Document Description: The Stock Span Problem for Class 8 2025 is part of Class 8 preparation. The notes and questions for The Stock Span Problem have been prepared according to the Class 8 exam syllabus. Information about The Stock Span Problem covers topics like and The Stock Span Problem Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for The Stock Span Problem.

Introduction of The Stock Span Problem in English is available as part of our Class 8 preparation & The Stock Span Problem in Hindi for Class 8 courses. Download more important topics, notes, lectures and mock test series for Class 8 Exam by signing up for free. Class 8: The Stock Span Problem - Class 8

Description

Full syllabus notes, lecture & questions for The Stock Span Problem - Class 8 - Class 8 | Plus excerises question with solution to help you revise complete syllabus | Best notes, free PDF download

Information about The Stock Span Problem

In this doc you can find the meaning of The Stock Span Problem defined & explained in the simplest way possible. Besides explaining types of The Stock Span Problem theory, EduRev gives you an ample number of questions to practice The Stock Span Problem tests, examples and also practice Class 8 tests.

Download as PDF

Top Courses for Class 8

View all courses for Class 8

MCQs

Semester Notes

Previous Year Questions with Solutions

video lectures

Summary

Sample Paper

mock tests for examination

The Stock Span Problem - Class 8

past year papers

Important questions

Viva Questions

study material

Objective type Questions

Exam

Extra Questions

pdf

practice quizzes

The Stock Span Problem - Class 8

shortcuts and tricks

ppt

The Stock Span Problem - Class 8

Free

;

Additional Information about The Stock Span Problem for Class 8 Preparation

The Stock Span Problem Free PDF Download

The The Stock Span Problem is an invaluable resource that delves deep into the core of the Class 8 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the The Stock Span Problem now and kickstart your journey towards success in the Class 8 exam.

Importance of The Stock Span Problem

The importance of The Stock Span Problem cannot be overstated, especially for Class 8 aspirants. This document holds the key to success in the Class 8 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

The Stock Span Problem Notes

The Stock Span Problem Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to The Stock Span Problem. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, The Stock Span Problem Notes on EduRev are your ultimate resource for success.

The Stock Span Problem Class 8 Questions

The "The Stock Span Problem Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study The Stock Span Problem on the App

Students of Class 8 can study The Stock Span Problem alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the The Stock Span Problem, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of The Stock Span Problem is prepared as per the latest Class 8 syllabus.

Education Revolution

Signup to see your scores go up
within 7 days!

Continue with Google

Takes less than 10 seconds to signup