Threaded Binary Tree - Class 8 PDF Download

Threaded Binary Tree

• Single Threaded: Where a NULL right pointers is made to point to the inorder successor (if successor exists)
• Double Threaded: Where both left and right NULL pointers are made to point to inorder predecessor and inorder successor respectively. The predecessor threads are useful for reverse inorder traversal and postorder traversal.

The threads are also useful for fast accessing ancestors of a node.
Following diagram shows an example Single Threaded Binary Tree. The dotted lines represent threads. 

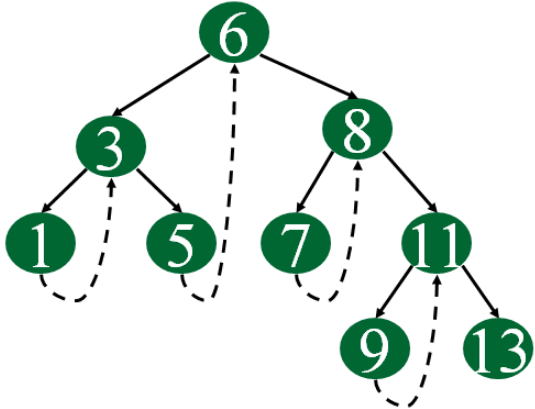
C representation of a Threaded Node
Following is C representation of a single-threaded node.

C

struct Node

{

    int data;

    struct Node *left, *right;

    bool rightThread; 

}

Java representation of a Threaded Node
Following is Java representation of a single-threaded node.

Java

static class Node

{

    int data;

    Node left, right;

    boolean rightThread; 

}

 

// This code contributed by aashish1995

Python3

class Node:

    def __init__(self, data,rightThread):

        self.data = data;

        self.left = None;

        self.right = None;

        self.rightThread = rightThread;

 

# This code is contributed by umadevi9616

C#

public class Node

{

   public int data;

   public Node left, right;

   public bool rightThread; 

}

 

// This code is contributed by aashish1995

Javascript

<script>

 class Node {

        constructor(val) {

            this.data = val;

            this.left = null;

            this.right = null;

            this.rightThread = false;

        }

    }

 

// This code contributed by aashish1995

</script>

Since right pointer is used for two purposes, the boolean variable rightThread is used to indicate whether right pointer points to right child or inorder successor. Similarly, we can add leftThread for a double threaded binary tree.

Inorder Traversal using Threads 
Following is code for inorder traversal in a threaded binary tree.

C

// Utility function to find leftmost node in a tree rooted

// with n

struct Node* leftMost(struct Node* n)

{

    if (n == NULL)

        return NULL;

 

    while (n->left != NULL)

        n = n->left;

 

    return n;

}

 

// C code to do inorder traversal in a threaded binary tree

void inOrder(struct Node* root)

{

    struct Node* cur = leftMost(root);

    while (cur != NULL) {

        printf("%d ", cur->data);

 

        // If this node is a thread node, then go to

        // inorder successor

        if (cur->rightThread)

            cur = cur->right;

        else // Else go to the leftmost child in right

             // subtree

            cur = leftmost(cur->right);

    }

}

Java

// Utility function to find leftmost node in a tree rooted

// with n

Node leftMost(Node n)

{

    if (n == null)

        return null;

 

    while (n.left != null)

        n = n.left;

 

    return n;

}

 

// C code to do inorder traversal in a threaded binary tree

static void inOrder(Node root)

{

    Node cur = leftMost(root);

    while (cur != null) {

        System.out.printf("%d ", cur.data);

 

        // If this node is a thread node, then go to

        // inorder successor

        if (cur.rightThread)

            cur = cur.right;

        else // Else go to the leftmost child in right

             // subtree

            cur = leftmost(cur.right);

    }

}

 

// This code contributed by aashish1995

Python3

# Utility function to find leftmost Node in a tree rooted

# with n

def leftMost(n):

 

    if (n == None):

        return None;

 

    while (n.left != None):

        n = n.left;

 

    return n;

 

 

# C code to do inorder traversal in a threaded binary tree

def inOrder(root):

 

    cur = leftMost(root);

    while (cur != None):

        print(cur.data," ");

 

        # If this Node is a thread Node, then go to

        # inorder successor

        if (cur.rightThread):

            cur = cur.right;

        else: # Else go to the leftmost child in right

             # subtree

            cur = leftmost(cur.right);

 

# This code is contributed by Rajput-Ji

C#

// Utility function to find leftmost node in a tree rooted

// with n

Node leftMost(Node n)

{

  if (n == null)

    return null;

 

  while (n.left != null)

    n = n.left;

 

  return n;

}

 

// C code to do inorder traversal in a threaded binary tree

static void inOrder(Node root)

{

  Node cur = leftMost(root);

  while (cur != null)

  {

    Console.Write("{0} ", cur.data);

 

    // If this node is a thread node, then go to

    // inorder successor

    if (cur.rightThread)

      cur = cur.right;

    else // Else go to the leftmost child in right

      // subtree

      cur = leftmost(cur.right);

  }

}

 

// This code is contributed by gauravrajput1

Javascript

<script>

 

// Utility function to find leftmost node in a tree rooted

// with n

function leftMost(n)

{

    if (n == null)

        return null;

  

    while (n.left != null)

        n = n.left;

  

    return n;

}

 

// JavaScript code to do inorder traversal in

// a threaded binary tree

function inOrder(root)

{

    let cur = leftMost(root);

    while (cur != null) {

        document.write(cur.data+" ");

  

        // If this node is a thread node, then go to

        // inorder successor

        if (cur.rightThread)

            cur = cur.right;

        else // Else go to the leftmost child in right

             // subtree

            cur = leftmost(cur.right);

        }

}

 

// This code is contributed by unknown2108

 

</script>

Following diagram demonstrates inorder order traversal using threads.

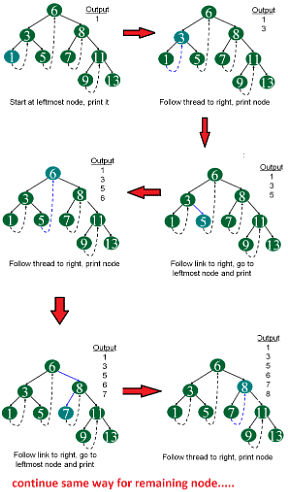
Advantages of Threaded Binary Tree

• In this Tree it enables linear traversal of elements.
• It eliminates the use of stack as it perform linear traversal.
• Enables to find parent node without explicit use of parent pointer.
• Threaded tree give forward and backward traversal of nodes by in-order fashion.
• Nodes contain pointers to in-order predecessor and successor.