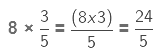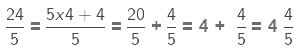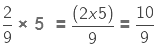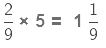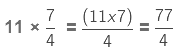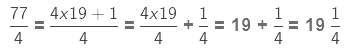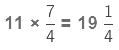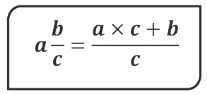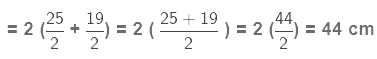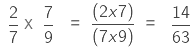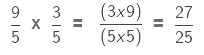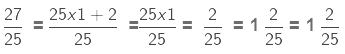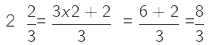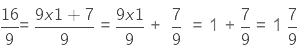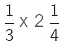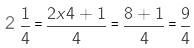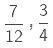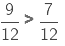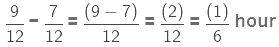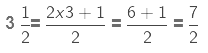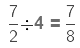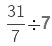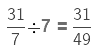Fractions and Decimals Class 7 Notes Maths Chapter 2
| Table of contents |

|
| Multiplication of Fractions |

|
| Fraction as an Operator ‘of’ |

|
| Multiplication of Decimal Numbers |

|
| Division of Decimal Numbers |

|
What is a Fraction?
A fraction represents a part of a whole. It consists of two numbers:
- Numerator: The top number, indicating how many parts are taken.
- Denominator: The bottom number, indicating the total number of equal parts in the whole.
Example: Write the fraction representing the shaded portion.
The given figure is divided into 4 equal parts.
Number of shaded parts = 3
Total number of equal parts = 4
Fraction representing the shaded portion = 3/4
Types of Fraction


Operations with Fractions
Addition:
- Same Denominator: Add the numerators, keep the denominator same.
- Different Denominators: Find a common denominator by multiplying with, then add.

Subtraction:
- Same Denominator: Subtract the numerators, keep the denominator same.
- Different Denominators: Find a common denominator, then subtract.

Multiplication of Fractions
1. Multiplication of a fraction by a whole number
Suppose there is an apple, you cut it into four equal parts.


Each part represents one – fourth of an apple.
or  (Whole Apple)
(Whole Apple)
Therefore, we can say that multiplication is repeated addition.
When we multiply a fraction by a whole number, we multiply the numerator of the fraction with the whole number keeping the denominator the same.
(a) 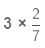
Here, we are multiplying a whole number by a proper fraction. So, we multiply the numerator of the fraction with the whole number and keep the denominator the same.
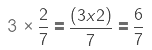
Let us see one example where we are multiplying a whole number by an improper fraction.
(b) 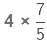
Here, the whole number is being multiplied by an improper fraction (the numerator is greater than the denominator). Again we multiply the numerator of the fraction with the whole number and keep the denominator the same.
As the product is an improper fraction, we express it as a mixed fraction.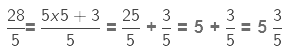
Multiply and reduce to lowest form:
Example 1. 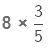
Sol:
Here, we are multiplying a whole number by a proper fraction (numerator is smaller than denominator). So, we multiply the numerator of the fraction with the whole number and keep the denominator the same.
Example 2.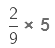
Sol:
A proper fraction is being multiplied by a whole number. So we multiply the numerator of the fraction with the whole number and keep the denominator the same.As the product is an improper fraction (numerator is greater than denominator), we express it as a mixed fraction.
Example 3.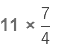
Sol:
We are multiplying a whole number by an improper fraction. So, we multiply the numerator of the fraction by the whole number and the denominator is kept the same.
Now, the product is an improper fraction, so we express it as a mixed fraction.
Example 4. A rectangular sheet of paper is 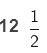 cm long and
cm long and 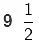 cm wide. Find its perimeter.
cm wide. Find its perimeter.
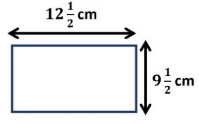
Sol:
Length of the rectangular sheet =cm
cm
Breadth of the rectangular sheet =
cm
cm
Perimeter of a rectangle = 2(l + b)
Perimeter of rectangular sheet of paper
Fraction as an Operator ‘of’
A pizza is divided into 8 equal slices.
Each slice represents 1/8th of pizza.
On combining four slices of pizza, we get

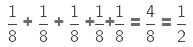
So, we say that 1/8 of 4 = 1/2

We say that ‘of’ represents multiplication.
1/2 of 10 is 1/2 x 10
We know that when we multiply a whole number by a fraction, we multiply the numerator of the fraction by the whole number and the denominator is kept the same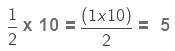
Examples: Find
(i) 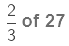
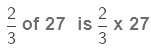
We multiply the numerator of the fraction by 27 and keep the denominator the same.
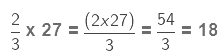
(ii) 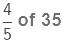
We multiply the numerator of the fraction by 35 and keep the denominator the same.
(iii) 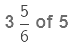
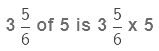

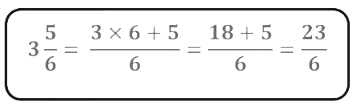
We again multiply the numerator of the fraction by 23 and keep the denominator the same.
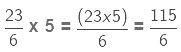
The product is an improper fraction, so we express it as a mixed fraction.
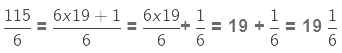
Multiplication of a Fraction by a Fraction
John has a bar of chocolate. He divided the chocolate bar into two equal parts and gave one part to his brother, Jason.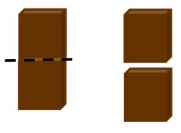
This part of chocolate represents 1/2 of whole or 1/2 of 1.

Now, Jason again divided his share of chocolate into two equal parts, then each of the two parts represents 1/2 of 1/2.
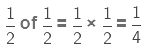
When we multiply a fraction by a fraction, we multiply their numerators and denominators.
Product of two fractions = 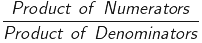

Here, we are multiplying two fractions, so we multiply their numerators and denominators.

Value of the Products
Consider the two proper fractions, 1/5 and 2/7.
Product of 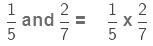
We multiply the numerators and denominators of the two fractions.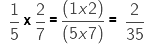
Now, we compare the two fractions, 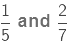 with their product, 2/35 Converting the two fractions to like fractions we get,
with their product, 2/35 Converting the two fractions to like fractions we get,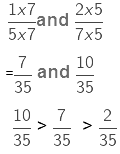
We see that the value of the product of two proper fractions is smaller than each of the two fractions.
Now, again consider two improper fractions, 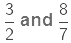
Product of, 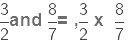
We multiply the numerators and denominators of the two fractions.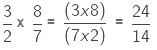
We multiply the numerators and denominators of the two fractions.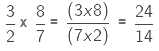
Now, comparing the two fractions, 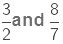 with their product 24/14
with their product 24/14
 (Converting the two fractions to like fractions)
(Converting the two fractions to like fractions)
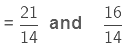
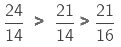
We see that the value of the product of two improper fractions is more than each of the two fractions.
Examples: Multiply and reduce to lowest form, tell whether the fraction obtained is proper or improper and if the fraction obtained is improper then convert it into a mixed fraction.
Example 1. 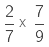
Sol:
As we are multiplying two fractions, we multiply their numerators and denominators.
14/63 is a proper fraction because the numerator is smaller than the denominator.
Example 2.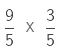
Sol:
We multiply the numerators and denominators of the two fractions.
27/25 is an improper fraction because the numerator is greater than the denominator and so we convert it into a mixed fraction.
Example 3. 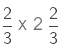
Sol:
We first change the mixed fraction to an improper fraction.
(multiplying the numerators and denominators of the two fractions)
= 16/9As 16/9 is an improper fraction (Numerator > Denominator), we convert it into a mixed fraction.
Example 4. Saahat reads 1/3 part of a book in 1 hour. How many parts of the book will he read in  hours?
hours?
Sol:
Part of the book read by Saahat in 1 hour = 1/3
Part of the book read by Saahat inhours =
We first change the mixed fraction to an improper fraction.
(multiplying the numerators and denominators of the two fractions)
= 3/4
Therefore, Saahat read 3/4 part of the book inhours.
Example 5. Michael finished coloring a picture in 7/12 hour. Vaibhav finished colouring the same picture in 3/4 hour. Who worked longer? By what fraction was it longer?
Sol:
Time taken by Michael to colour the picture = 7/12 hour
Time taken by Vaibhav to colour the same picture = 3/4 hour
The two fractions are unlike, so we first convert them to like fractions (fractions having same denominator).
LCM of 12 and 4 = 2 × 2 × 3 = 12
On comparing the two fractions we get,
Therefore, Vaibhav worked longer by
Division of Fraction
Multiply by the reciprocal (flip the second fraction).
Example:
Division of Whole Numbers by a Fraction
Ethan’s mother brings a jar full of lemonade and pours 1/3 liters into each glass.
Can you tell how many glasses of lemonade she will get if the capacity of the jar of lemonade is 2 liters?
To find the number of glasses we divide 2 liters (capacity of the jar) by 1/3 (quantity of lemonade in each glass).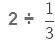 = Number of glasses obtained when 2 liters is divided into equal parts
= Number of glasses obtained when 2 liters is divided into equal parts
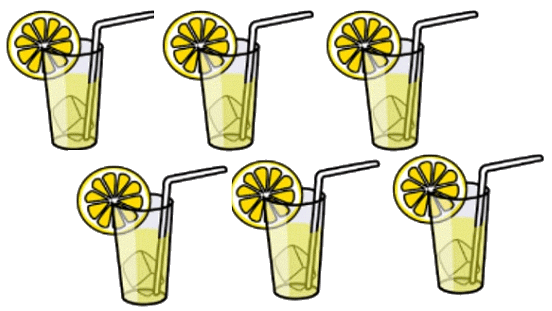
Here 3 is the reciprocal of 1/3.
The non-zero numbers whose product with each other is 1, are called reciprocals of each other.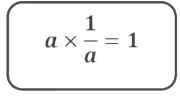
So, reciprocal of 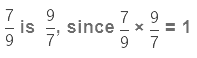
Reciprocal of a fraction
1. When we divide a whole number by any fraction, we multiply that whole number by the reciprocal of that fraction.
Reciprocal of 2/5 is 5/2.

Now, we multiply 7 by the reciprocal of 2/5.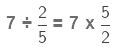
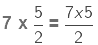 (Multiplying numerator of the fraction by the whole number)
(Multiplying numerator of the fraction by the whole number)
= 35/2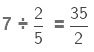
2. While dividing a whole number by a mixed fraction, first convert the mixed fraction into an improper fraction and then solve it.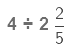
We first convert the mixed fraction into an improper fraction.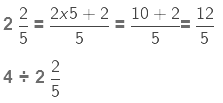

Reciprocal of 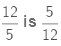
Now, we multiply 4 by the reciprocal of 12/5.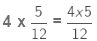
(Multiplying numerator of the fraction by the whole number)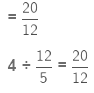
 |
Download the notes
Chapter Notes: Fractions & Decimals
|
Download as PDF |
Division of Fraction by a Whole Number
Suppose you have a bar of chocolate.
Now, you have to divide three – fourth of the chocolate into three equal parts. How will you do it?
Let’s do it step by step.

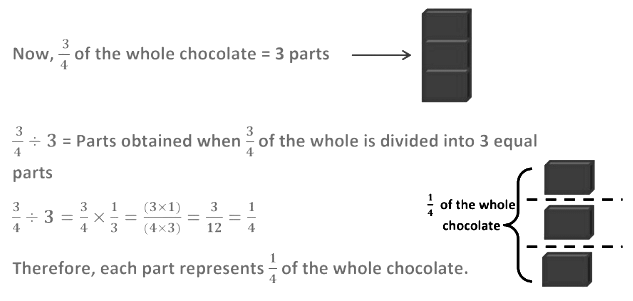
When we divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number.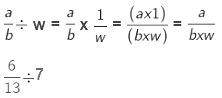
We will multiply the fraction by the reciprocal of the whole number. Reciprocal of 7 = 1/7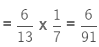
Examples: Find,
Example 1. 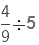
Sol:
Reciprocal of 5 = 1/5
Next, we multiply the fraction with reciprocal of 5.(Multiplying the numerators and denominators of fractions)
= 4/45
Example 2.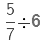
Sol:
Reciprocal of 6 = 1/6(multiplying the fraction with reciprocal of 5)
(Multiplying the numerators and denominators of fractions)
= 5/12
Example 3. 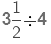
Sol:
Reciprocal of 4 = 1/4
(multiplying the fraction with reciprocal of 4)
(multiplying the numerators and denominators of fractions)
Example 4. 
Sol:(converting mixed fraction into improper fraction)
Reciprocal of 7 = 1/7
(multiplying the fraction with reciprocal of 7)
(multiplying the numerators and denominators of fractions)
Division of a Fraction by Another Fraction
John has a bar of chocolate. He divided the chocolate bar into two equal parts and gave one part to his brother, Jason.
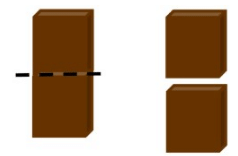
This part of chocolate represents 1/2 of whole or 1 divided by 2.

Now, Jason again divided his share of chocolate into two equal parts, then each of the two parts represents 1/2 divided by 2 .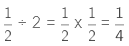

When we divide a fraction by a fraction, we multiply the numerator by denominator and denominator by numerator.
Division of two fractions = 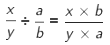
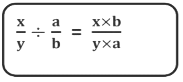
For Example, 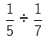
Here, we are multiplying two fractions, so we multiply their numerators and denominators.
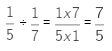
Example: Solve the following
(i) It is given that 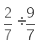
Now
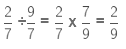
(ii) It is given that 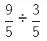
Now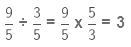
(iii) It is given that 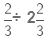
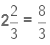
Now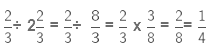
(iv) It is given that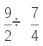
Now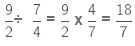
Example: Sushant reads 1/3 part of a book in 2 hours. How many parts of the book will he read in 1 hour?
Part of the book read by Sushant in 2 hours = 1/3
Part of the book read by Sushant in 1 hour =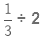
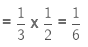
Therefore, Sushant read 1/6 part of the book in 1 hour.

Introduction to Decimals
The numbers expressed in decimal forms are called decimals.
Decimals have a decimal part and a whole number part. The point is used to separate these parts.
The number on the left side of decimal is the whole number part and the number formed by the digits at the right side of the decimal is called decimal part.

Place Values of Decimals
Let’s revise the place value chart of decimal numbers
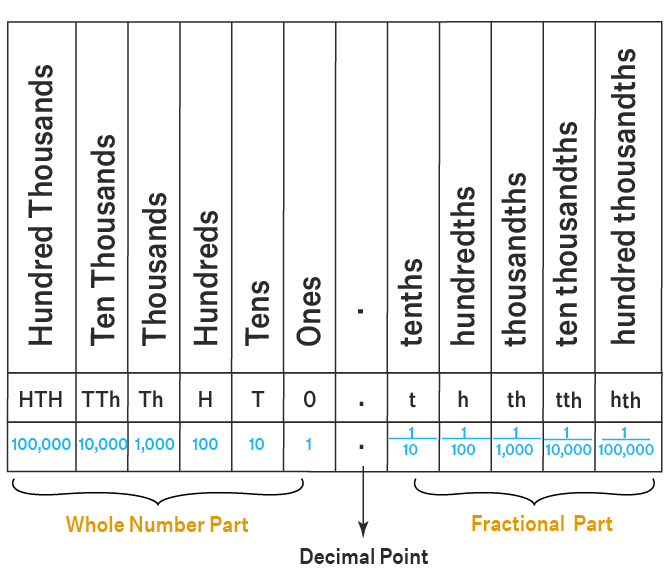 Place Value Chart
Place Value Chart
Example: Arrange the given decimal numbers in the place value chart and also write their expanded form.
(i) 21.6
(ii) 305.64
(iii) 3.289
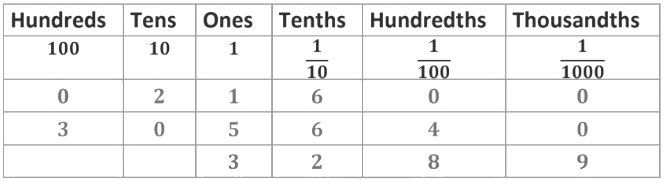
(i) 21. 6 = 2 × 10 + 1 × 1 + 6 x 1/10
(ii) 305. 64 = 3 × 100 + 0 × 10 + 5 × 1 + 6 × 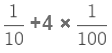
(iii) 3. 289 = 3 × 1 + 2 × 1/10 + 8 x 1/100 + 9 x 1/1000
Comparing Decimals
Consider the decimals, 28.43 and 28.67.
If we have to compare the given decimals, we follow the following steps.
1. We first compare the whole-number part (starting from the leftmost digit)
In the given decimals, 28.43 and 28.67 we see that the digits, 2 and 8 to the left of the decimal point are the same in both the decimals.
2. If the whole number parts are equal, then we compare the digits on the right of the decimal point starting from the tenths place.
Digits at tenths place of the decimals, 28.43 and 28.67 are 4 and 6 respectively.
Now, 6 > 4
Therefore 28.67 > 28.43
Example: Which is greater?
(i) 0.5 or 0.05
We compare the whole number parts (digit to the left of the decimal point) of the decimals, 0.5 and 0.05. Clearly, it is the same in both the decimals.Next, we compare the digits at the tenths place of 0.5 and 0.05.
Now, 5 > 0.
Therefore, 0.5 > 0.05.
(ii) 1.47 or 1.49
Comparing the whole number parts of the decimals, 1.47 and 1.49 (digit to the left of the decimal point) we see that it is the same in both the numbers.
Next, we compare the tenths digits of the decimals, 1.47 and 1.49. Clearly, the tenths digit is also the same in both the numbers.
We compare the hundredths digit of the decimals, 1.47 and 1.49.
Now, 9 > 7. So, 1.49 > 1.47
Addition and Subtraction of Decimals
1. Add 0.19 + 2.3
Decimal numbers, 0.19 and 2.3 have two digits and one digit respectively to the right of the decimal point. So, we add a zero to the right of 2.3.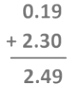

2. Subtract 39.87 – 21.98
Decimals numbers 39.87 and 21.98 have the same number of zeros after the decimal point.
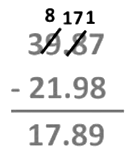
Example: Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?
Sol:
Distance travelled by Dinesh
= Distance from A to B + Distance from B to C
=7.5 km + 12.7 km

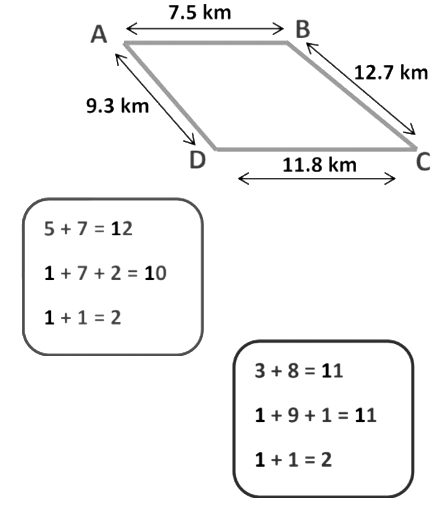
Distance travelled by Dinesh = 20.2 km
Distance travelled by Ayub
=Distance from A to D + Distance from D to C
= 9.3 km + 11.8 km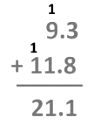
Distance travelled by Ayub = 21.1 km
We see that the distance travelled by Ayub is more than the distance travelled by Dinesh.
Difference = 21.1 km – 20.2 km

So, Ayub travelled 0.9 km more than Dinesh.
Multiplication of Decimal Numbers
We will now learn the multiplication of two decimal numbers.
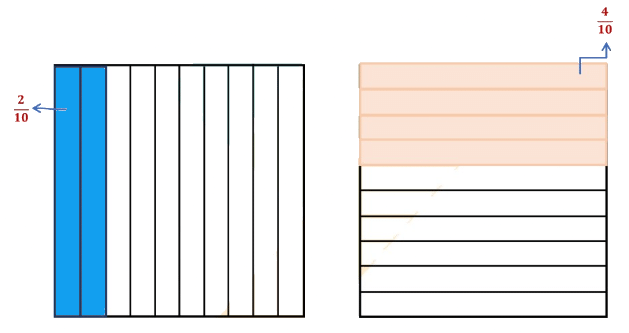
Consider two decimal numbers, 0.2 and 0.4.
Let us now find 0.2 × 0.4,
(a) Take a square and divide it into 10 equal parts.
(b) 0.2 or 2/10 represents 2 parts out of 10 equal parts
(c) Similarly, 0.4 or 4/10 represents 4 parts out of 10 equal parts.
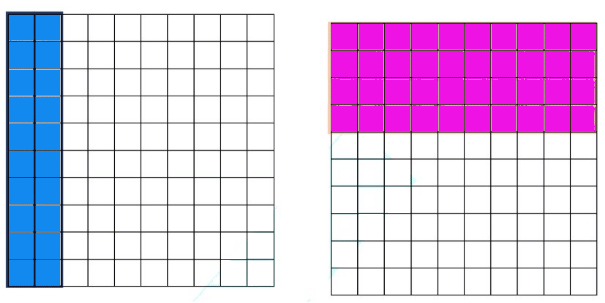
(d) If we divide each small rectangle into 10 equal parts, we get 100 small squares.
We know,
0.2 is same as 0.20
2 tenths = 2 hundredths (20 small squares out of hundred)
Similarly, 4 tenths = 4 hundredths (40 small squares out of a hundred)
If we overlap the two grids, we see that 8 small squares out of 100 are common to both.
(8/100 or 0.08)
The yellow region represents 0.2 × 0.4
Thus, 0.2 × 0.4 = 0.08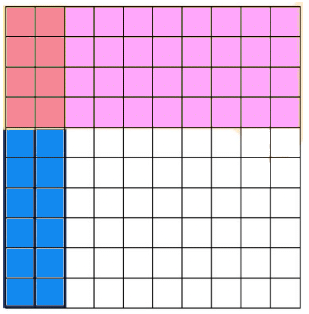
Multiplication of Decimal Numbers
(i) Multiply the given decimal numbers without a decimal point just like whole numbers.
(ii) Put the decimal point in the product by counting as many places from right to left as the sum of the decimal places of the decimals being multiplied.
Find 2.7 × 1.3
First, multiply the given decimals as whole numbers.
On multiplying 27 and 13 we get,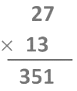
We see that in 2.7 and 1.3, there is 1 digit to the right of the decimal point.
Now, 1 + 1 = 2. So, we count 2 digits from the rightmost digit (i.e., 1) in 351 and move towards left and put the decimal point there.
Example: Find 10.05 × 1.05
Sol:
10.05 × 1.05
We first multiply the given decimals as whole numbers.
Number of decimal places in 10.05 = 2
Number of decimal places in 1.05 = 2Now, 2 + 2 = 4. So, we count 4 digits from the rightmost digit in 105525 and put the decimal point there.
Multiplication of Decimal Numbers by 10, 100, 1000
When a decimal number is multiplied by 10, 100 or 1000, the digits in the product are the same as in the decimal number but the decimal point in the product is shifted to the right by as many places as there are zeros over one.
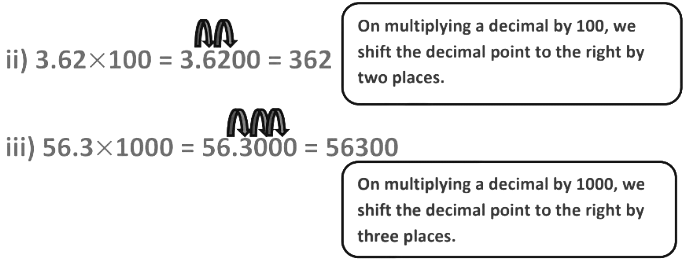
Example: Find the product
(i) 36.75× 10 = 367.5
When we multiply a decimal number by 10, we shift the decimal point to the right by 1 place(ii) 3.62 × 100 = 362.0
On multiplying a decimal number by 100, we shift the decimal point to the right by 2 places.
(iii)0.03 × 1000 = 030.0 = 30
When we multiply a decimal number by 1000, we shift the decimal point to the right by 3 places.
Division of Decimal Numbers
Division of Decimal Numbers by 10, 100, 1000
While dividing a number by 10, 100 or 1000, the digits of the number and the quotient are the same but the decimal point in the quotient shifts to the left by as many places as there are zeros over one.

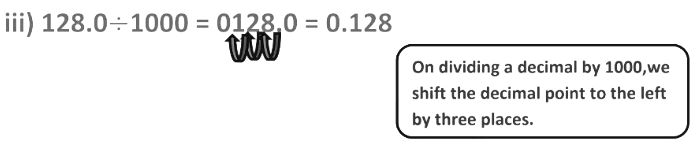
Example: Find
(i) 33.2 ÷ 10 = 3.32 (Shifting decimal point to the left by 1 place)
(ii) 2.8 ÷ 100 = 0.028 (Shifting decimal point to the left by 2 places)
(iii) 127.9 ÷ 1000 = 0.1279 (Shifting decimal point to the left by 3 places)
Division of a Decimal Number by Another Whole Number
(i) Divide the decimal number, treating it as a whole number by the given whole number.
(ii) Put the decimal point at the same number of decimal places as in the given decimal.
Divide: 65.4 ÷ 6
Dividing the decimal number as the whole number by the given whole number we get,
654 ÷ 6 = 109
In the decimal number 65.4, the number of decimal places is 1. So, we put the decimal point at the same place.
65.4 ÷ 6 = 10.9
Example:
Find 651.2 ÷ 4
We divide the decimal number as the whole number by the given whole number,
6512 ÷ 4 = 1628
We put the decimal point at the same decimal place as in 651.2.
651.2 ÷ 4 = 162.8
Division of a Decimal Number by Another Decimal Number
(i) We multiply the dividend and divisor by 10, 100 or 1000 etc. to convert the divisor into a whole number.
(ii) Now, divide the new dividend by the whole number.
Divide: 3.25÷ 0.5
As the number of decimal places in the divisor, 0.5 is 1 we multiply the numerator and denominator by 10.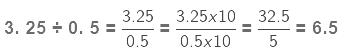
Example:
(i) 0.5 ÷ 0.25The number of decimal places in the divisor, 0.25 is 2 so we multiply the numerator and denominator by 100.
|
77 videos|388 docs|39 tests
|
FAQs on Fractions and Decimals Class 7 Notes Maths Chapter 2
| 1. How do you multiply fractions? |  |
| 2. What does the term 'of' mean in relation to fractions? |  |
| 3. How do you multiply decimal numbers? |  |
| 4. What is the procedure for dividing decimal numbers? |  |
| 5. Can you simplify fractions after multiplying them? |  |