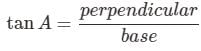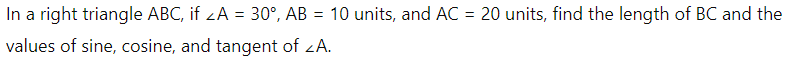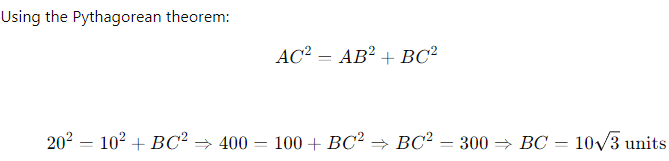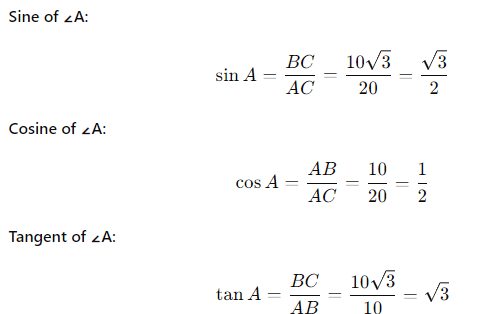Introduction to Trigonometry Class 10 Notes Maths Chapter 8
| Table of contents |

|
| Introduction |

|
| Trigonometric Ratios |

|
| Trigonometric Ratios of Some Specific Angles |

|
| Trigonometric Identities |

|
| Summary |

|
Introduction
Trigonometry is a math branch studying relationships between the sides and angles of a triangle.
- The name comes from Greek words meaning three sides and measure.
- Trigonometry's roots go back to Egypt and Babylon, where it helped astronomers measure distances to stars.
- Today, it's crucial in Engineering and Physical Sciences.
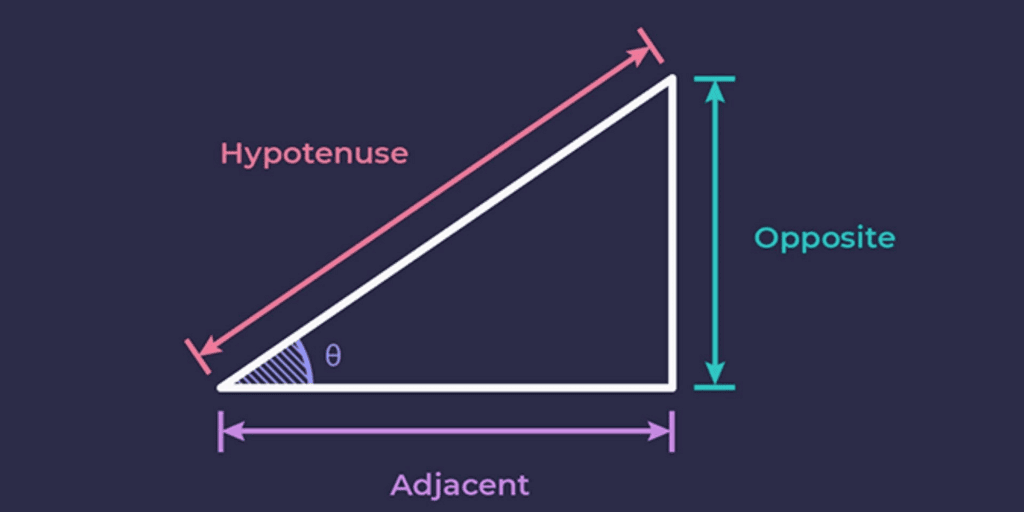
In this chapter, we will delve into trigonometric ratios, specifically examining the ratios of the sides of a right triangle in relation to its acute angles. Our focus will initially be on acute angles, though these ratios extend to other angle measures as well. We will also introduce trigonometric ratios for angles of 0° and 90°.
Trigonometric Ratios
Trigonometric ratios are terms defined for specific ratios of sides. They vary greatly and are used according to the need. Since all of these ratios are defined for right angled triangles, we will define them using name of sides as Hypotenuse, Perpendicular and Base.
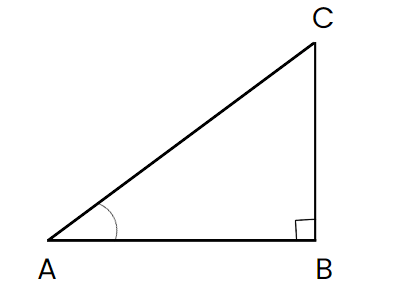
Referring to the Right Triangle ABC in the following figure:
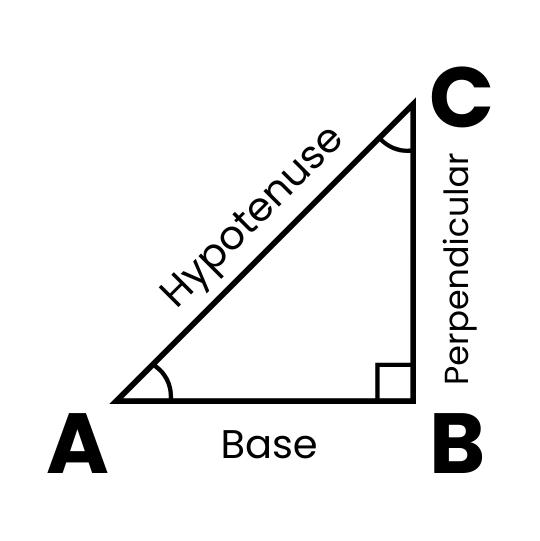 Right Triangle ABC
Right Triangle ABC


Here, θ is pronounced as theta.
 Formulae for Trigonometric Ratios
Formulae for Trigonometric Ratios
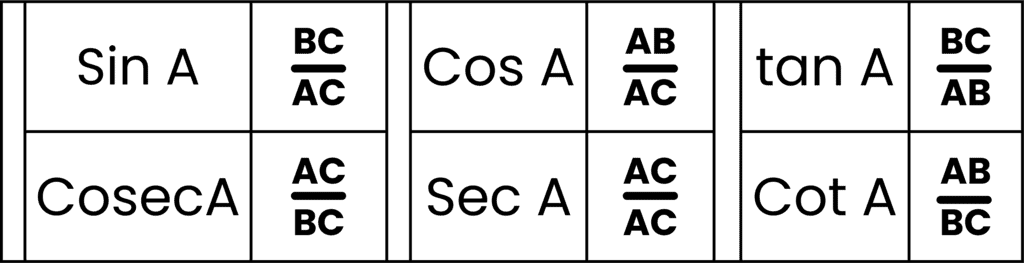 Ratio Formula
Ratio Formula
Relation between Trigonometric Ratios
- cosec θ =1/sin θ
- sec θ = 1/cos θ
- tan θ = sin θ/cos θ
- cot θ = cos θ/sin θ=1/tan θ
Example 1: Suppose a right-angled triangle ABC, right-angled at B such that hypotenuse AC = 5 cm, base BC = 3 cm and perpendicular AB = 4 cm. Also, ∠ACB = θ. Find the trigonometric ratios tan θ, sin θ and cos θ.
Solution: Given, in ∆ABC,
Hypotenuse, AC = 5 cm
Base, BC = 3 cm
Perpendicular, AB = 4 cm
Then, by the trigonometric ratios, we have;
tan θ = Perpendicular/Base = 4/3
Sin θ = Perpendicular/Hypotenuse = AB/AC = 4/5
Cos θ = Base/Hypotenuse = BC/AC = 3/5
Example 2:
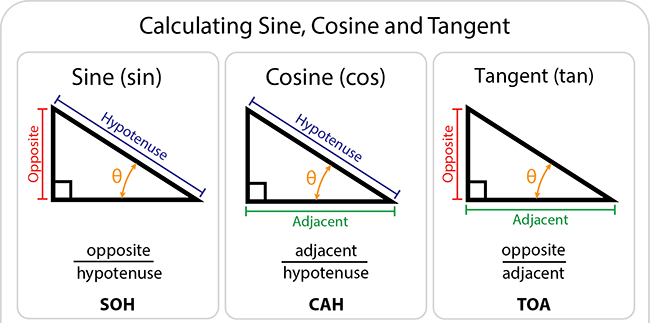 Mnemonic to calculate Sine, Cosine & Tangent
Mnemonic to calculate Sine, Cosine & Tangent
Trigonometric Ratios of Some Specific Angles
In geometry, you've already learned how to create angles of 30°, 45°, 60°, and 90°. Now, let us explore the trigonometric ratios' values for these specific angles and, naturally, for 0°
Hypotenuse is the longest side of a right-angled triangle, opposite the right angle.
Also, by Pythagoras theorem, we know that (Hypotenuse)2 = (Base)2 + (Perpendicular)2.
1. Trigonometric Ratios of 45°
If one of the angles of a right-angled triangle is 45°, then another angle will also be equal to 45°.
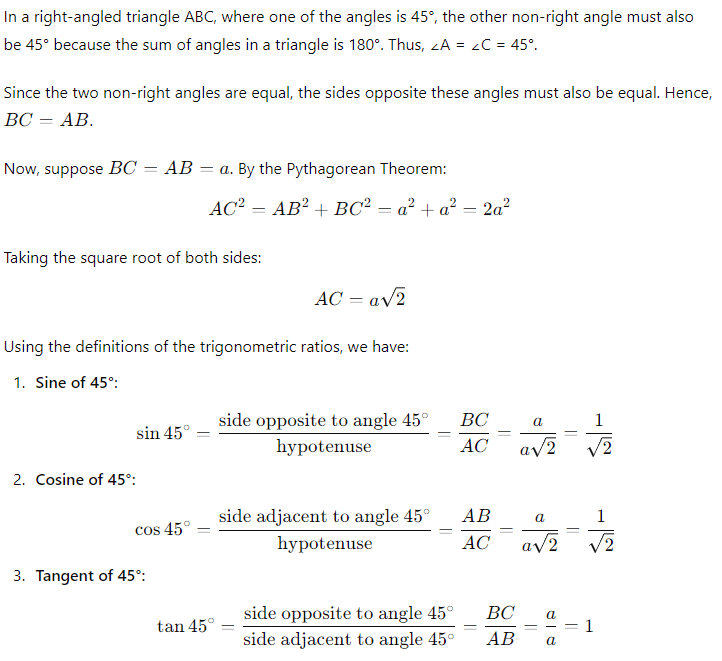
2. Trigonometric Ratios of 30° and 60°
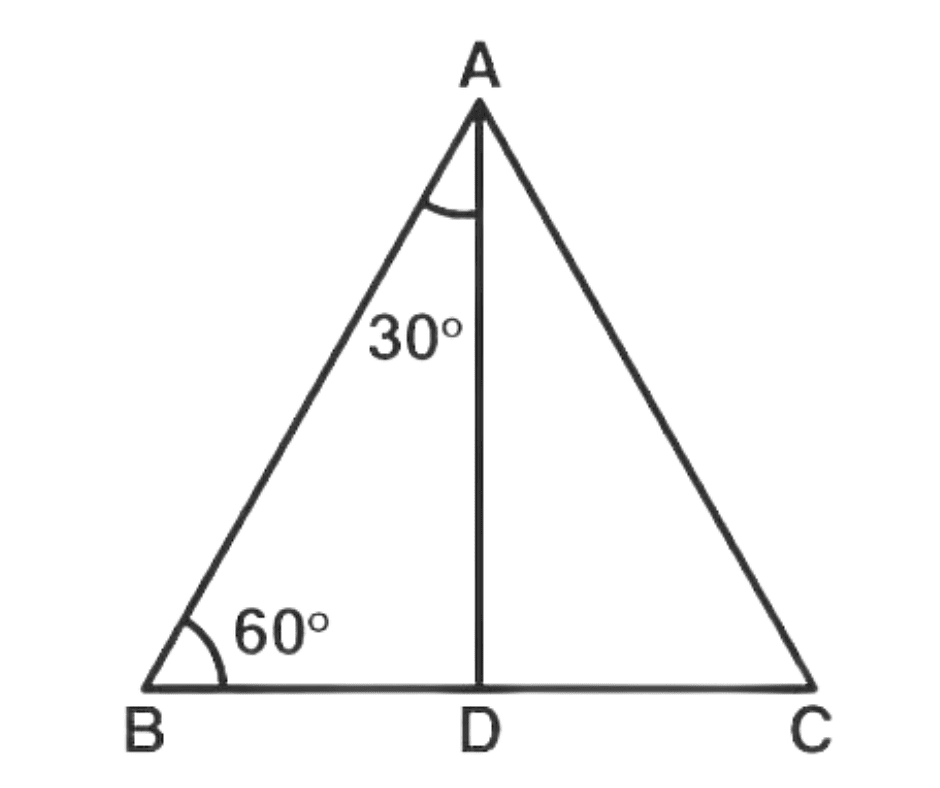 Equilateral Triangle
Equilateral Triangle


3. Trigonometric Ratios of 0° and 90°
If ABC is a right-angled triangle at B, if ∠A is reduced, then side AC will come near to side AB. So, if ∠ A is nearing 0 degree, then AC becomes almost equal to AB, and BC gets almost equal to 0.
Hence, Sin A = BC /AC = 0
and cos A = AB/AC = 1
tan A = sin A/cos A = 0/1 = 0
Also,
cosec A = 1/sin A = 1/0 = not defined
sec A = 1/cos A = 1/1 = 1
cot A = 1/tan A = 1/0 = not defined
In the same way, we can find the values of trigonometric ratios for a 90-degree angle. Here, angle C is reduced to 0, and the side AB will be nearing side BC such that angle A is almost 90 degrees and AB is almost 0.
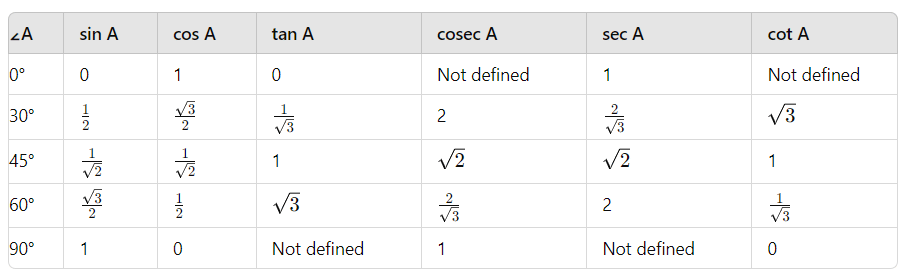 Trigonometric Ratio Table
Trigonometric Ratio Table
Standard Values of Trigonometric Ratios
Example 1: Evaluate 2 tan2 45° + cos2 30° – sin2 60°.
Solution: Since we know,
tan 45° = 1
cos 30° = √3/2
sin 60° = √3/2
Therefore, putting these values in the given equation:
2(1)2 + (√3/2)2 – (√3/2)2
= 2 + 0
= 2
Example 2: If tan (A + B) =√3 and tan (A – B) =1/√3, 0° < A + B ≤ 90°; A > B, find A and B.
Solution: Given,
tan (A + B) = √3
As we know, tan 60° = √3
Thus, we can write;
⇒ tan (A + B) = tan 60°
⇒(A + B) = 60° …… (i)
Now again given;
tan (A – B) = 1/√3
Since, tan 30° = 1/√3
Thus, we can write;
⇒ tan (A – B) = tan 30°
⇒(A – B) = 30° ….. (ii)
Adding the equation (i) and (ii), we get;
A + B + A – B = 60° + 30°
2A = 90°
A= 45°
Now, put the value of A in eq. (i) to find the value of B;
45° + B = 60°
B = 60° – 45°
B = 15°
Therefore A = 45° and B = 15°
Example 3: Show that :
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:
(i) tan 48° tan 23° tan 42° tan 67°
We can also write the above given tan functions in terms of cot functions, such as;
tan 48° = tan (90° – 42°) = cot 42°
tan 23° = tan (90° – 67°) = cot 67°
Hence, substituting these values, we get
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° tan 42°) (cot 67° tan 67°)
= 1 × 1 [since cot A.tan A = 1]
= 1
(ii) cos 38° cos 52° – sin 38° sin 52°
We can also write the given cos functions in terms of sin functions.
cos 38° = cos (90° – 52°) = sin 52°
cos 52°= cos (90° – 38°) = sin 38°
Hence, putting these values in the given equation, we get;
sin 52° sin 38° – sin 38° sin 52° = 0
Example 4: If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution: Given,
tan 2A = cot (A – 18°)
As we know by trigonometric identities,
tan 2A = cot (90° – 2A)
Substituting the above equation in the given equation, we get;
⇒ cot (90° – 2A) = cot (A – 18°)
Therefore,
⇒ 90° – 2A = A – 18°
⇒ 108° = 3A
A = 108° / 3
Hence, the value of A = 36°
Example 5: If A, B and C are interior angles of a triangle ABC, then show that sin [(B + C)/2] = cos A/2.
Solution:
As we know, for any given triangle, the sum of all its interior angles is equals to 180°.
Thus,
A + B + C = 180° ….(1)
Now we can write the above equation as;
⇒ B + C = 180° – A
Dividing by 2 on both the sides;
⇒ (B + C)/2 = (180° – A)/2
⇒ (B + C)/2 = 90° – A/2
Now, put sin function on both sides.
⇒ sin (B + C)/2 = sin (90° – A/2)
Since,
sin (90° – A/2) = cos A/2
Therefore,
sin (B + C)/2 = cos A/2
Trigonometric Identities
In trigonometry, an equation involving trigonometric ratios of an angle is called a trigonometric identity if it holds true for all values of the angle(s) involved. Let’s prove three fundamental trigonometric identities and understand their significance.
Identity 1
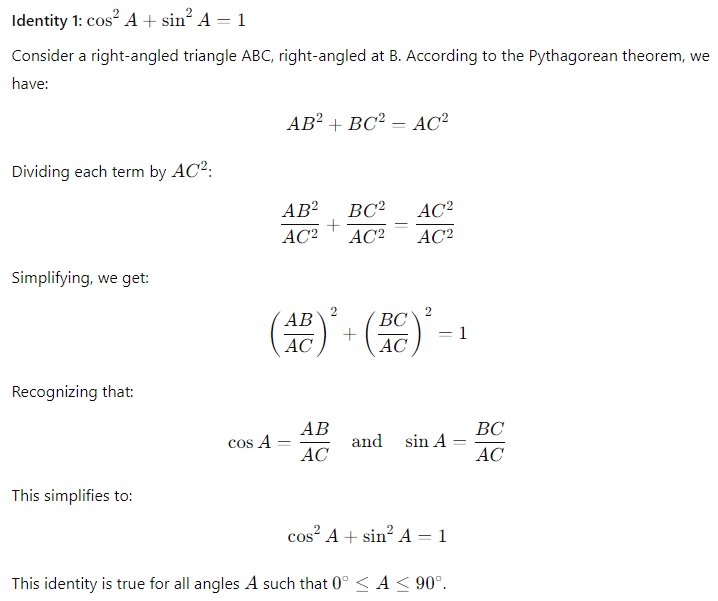
Identity 2
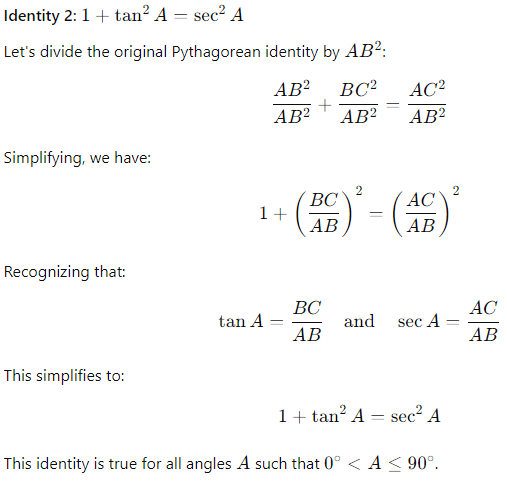
Identity 3
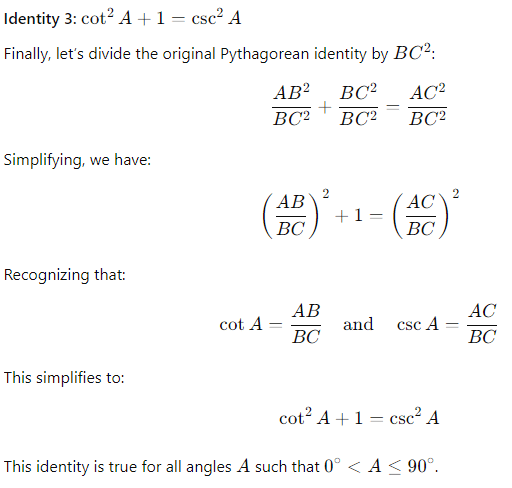
Example 6: Prove the identities:
(i) √[1 + sinA/1 – sinA] = sec A + tan A
(ii) (1 + tan2A/1 + cot2A) = (1 – tan A/1 – cot A)2 = tan2A
Solution:
(i) Given:√[1 + sinA/1 – sinA] = sec A + tan A
(ii) Given: (1 + tan2A/1 + cot2A) = (1 – tan A/1 – cot A)2 = tan2A
LHS:
= (1+tan²A) / (1+cot²A)
Using the trigonometric identities we know that 1+tan²A = sec²A and 1+cot²A= cosec²A
= sec²A/ cosec²A
On taking the reciprocals we get= sin²A/cos²A
= tan²A
RHS:
=(1-tanA)²/(1-cotA)²
Substituting the reciprocal value of tan A and cot A we get,
= (1-sinA/cosA)²/(1-cosA/sinA)²
= [(cosA-sinA)/cosA]²/ [(sinA-cos)/sinA)²] = [(cosA-sinA)²×sin²A] /[cos²A. /(sinA-cosA)²] = sin²A/cos²A
= tan2A
The values of LHS and RHS are the same.
Hence proved.
Example 7: If sin θ + cos θ = √3, then prove that tan θ + cot θ = 1.
Solution:
Given,
sin θ + cos θ = √3
Squaring on both sides,
(sin θ + cos θ)2 = (√3)2
sin2θ + cos2θ + 2 sin θ cos θ = 3
Using the identity sin2A + cos2A = 1,
1 + 2 sin θ cos θ = 3
2 sin θ cos θ = 3 – 1
2 sin θ cos θ = 2
sin θ cos θ = 1
sin θ cos θ = sin2θ + cos2θ
⇒ (sin2θ + cos2θ)/(sin θ cos θ) = 1
⇒ [sin2θ/(sin θ cos θ)] + [cos2θ/(sin θ cos θ)] = 1
⇒ (sin θ/cos θ) + (cos θ/sin θ) = 1
⇒ tan θ + cot θ = 1
Hence proved.
Example 8: Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
cot 85° + cos 75°
= cot (90° – 5°) + cos (90° – 15°)
We know that cos(90° – A) = sin A and cot(90° – A) = tan A
= tan 5° + sin 15°
Summary
1. Trigonometric Ratios in a Right Triangle:
- sin A = side opposite to angle A / hypotenuse
- cos A = side adjacent to angle A / hypotenuse
- tan A = side opposite to angle A / side adjacent to angle A .
2. Reciprocal Trigonometric Ratios:
- cosec A = 1/sin A
- sec A = 1/cos A
- tan A = 1/cot A
- tan A = sin A/cos A
3. Relation between Trigonometric Ratios:
- If one trigonometric ratio of an acute angle is known, the others can be easily determined.
4. Values for Specific Angles:
- Values of trigonometric ratios for angles 0°, 30°, 45°, 60°, and 90°.
5. Limitations and Inequalities:
- The value of sin A or cos A never exceeds 1.
- Wheras, the value of sec A or cosec A is always greater than or equal to 1.
6. Trigonometric Identities:
- sin2A+cos2A = 1
- sec2A−tan2A=1 (for 0°≤A<90°)
- cosec2A=1+cot2A (for 0°<A≤90°)
|
127 videos|584 docs|79 tests
|
FAQs on Introduction to Trigonometry Class 10 Notes Maths Chapter 8
| 1. What are the basic trigonometric ratios? |  |
| 2. Can you explain the trigonometric ratios of some specific angles? |  |
| 3. What are trigonometric identities? |  |
| 4. How can trigonometric identities be used in problem-solving? |  |
| 5. Can you give an example of how trigonometric ratios are applied in real-world situations? |  |