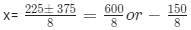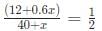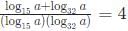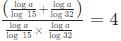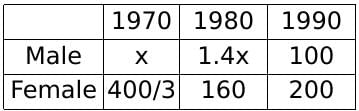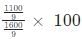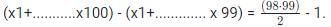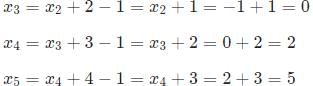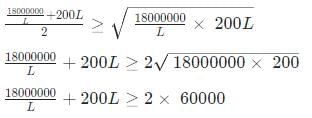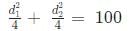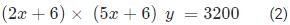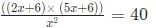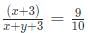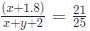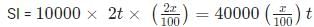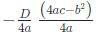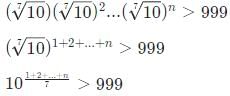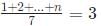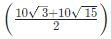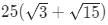Directions: For the following questions answer them individually.
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:A shop owner bought a total of 64 shirts from a wholesale market that came in two sizes, small and large. The price of a small shirt was INR 50 less than that of a large shirt. She paid a total of INR 5000 for the large shirts, and a total of INR 1800 for the small shirts. Then, the price of a large shirt and a small shirt together, in INR, is
Explanation
Let the number of large shirts be l and the number of small shirts be s.
Let the price of a small shirt be x and that of a large shirt be x + 50.
Now, s + l = 64
l (x + 50) = 5000
sx = 1800
Adding them, we get,
lx + sx + 50l = 6800
64x + 50l = 6800
Substituting l = (6800 - 64x) / 50, in the original equation, we get
(6800 - 4x)/50 (x + 50) = 5000
(6800 - 64x)(x + 50) = 250000
6800x + 340000 − 64x2 − 3200x = 250000
64x2 − 3600x − 90000 = 0
Solving, we get,
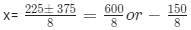
So, x = 75
x + 50 = 125
Answer = 75 + 125 = 200.
Alternate approach: By options.
Hint: Each option gives the sum of the costs of one large and one small shirt. We know that large = small + 50
Hence, small + small + 50 = option.
SMALL = (Option - 50)/2
LARGE = Small + 50 = (Option + 50)/2
Option A and Option D gives us decimal values for SMALL and LARGE, hence we will consider them later.
Lets start with Option B.
Large = 150 + 50 / 2 = 100
Small = 150 - 50 / 2 = 50
Now, total shirts = 5000/100 + 1800/50 = 50 + 36 = 86 (X - This is wrong)
Option C
Large = 200 + 50 / 2 = 125
Small = 200 - 50 / 2 = 75
Total shirts = 5000/125 + 1800/75 = 40 + 24 = 64 (This is the right answer)
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:One day, Rahul started a work at 9 AM and Gautam joined him two hours later. They then worked together and completed the work at 5 PM the same day. If both had started at 9 AM and worked together, the work would have been completed 30 minutes earlier. Working alone, the time Rahul would have taken, in hours, to complete the work is
Explanation
Let Rahul work at a units/hr and Gautam at b units/hour
Now as per the condition :
8a + 6b = 7.5a + 7.5b
so we get 0.5a = 1.5b
or a = 3b
Therefore total work = 8a + 6b = 8a + 2a = 10a
Now Rahul alone takes 10a/10 = 10 hours.
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be
Explanation
Initially number of matches = 40
Now matches won = 12
Now let remaining matches be x
Now number of matches won = 0.6x
Now as per the condition :
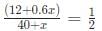
24 +1.2x = 40 + x
0.2x = 16
x = 80
Now when they won 90% of remaining = 80(0.9) = 72
So total won = 84
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:The number of distinct pairs of integers (m,n), satisfying ∣1 + mn ∣ < ∣ m + n ∣ < 5 is:
Explanation
Let us break this up into 2 inequations [ Let us assume x as m and y as n ]
| 1 + mn | < | m + n |
| m + n | < 5
Looking at these expressions, we can clearly tell that the graphs will be symmetrical about the origin.
Let us try out with the first quadrant and extend the results to the other quadrants.
We will also consider the +X and +Y axes along with the quadrant.
So, the first inequality becomes,
1 + mn < m + n
1 + mn - m - n < 0
1 - m + mn - n < 0
(1-m) + n(m-1) < 0
(1-m)(1-n) < 0
(m - 1)(n - 1) < 0
Let us try to plot the graph.
If we consider only mn < 0, then we get
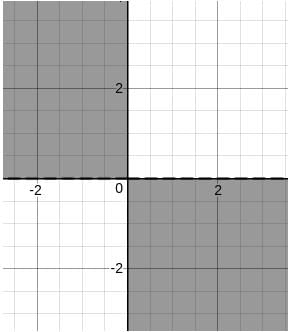
But, we have (m - 1)(n - 1) < 0, so we need to shift the graphs by one unit towards positive x and positive y.
So, we have,
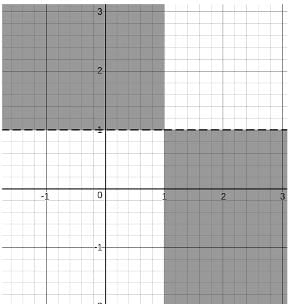
But, we are only considering the first quadrant and the +X and +Y axes. Hence, if we extend, we get the following region.
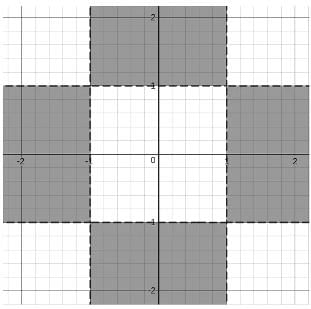
So, if we look for only integer values, we get
(0,2), (0,3),.......
(0,-2), (0, -3),......
(2,0), (3,0), ......
(-2,0), (-3,0), .......
Now, let us consider the other inequation as well, in which |x + y| < 5
Since one of the values is always zero, the modulus of the other value is less than or equal to 4.
Hence, we get
(0,2), (0,3), (0,4)
(0,-2), (0, -3), (0, -4)
(2,0), (3,0), (4,0)
(-2,0), (-3,0), (-4,0)
Hence, a total of 12 values.
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:For a real number a, if 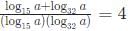 then a must lie in the range
then a must lie in the range
Explanation
We have :
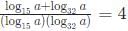
We get
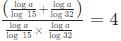
we get log a (log32 +l og 15) = 4(log a)2
we get (log32 + log 15) = 4loga
= log480 = loga4
= a4 = 480
so we can say a is between 4 and 5 .
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is
Explanation
Let us solve this question by assuming values(multiples of 100) and not variables(x).
Since we know that the female population was twice the male population in 1990, let us assume their respective values as 200 and 100.
Note that while assuming numbers, some of the population values might come out as a fraction(which is not possible, since the population needs to be a natural number). However, this would not affect our answer, since the calculations are in ratios and percentages and not real values of the population in any given year.
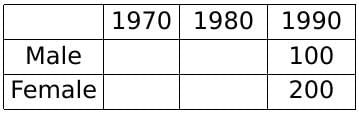
Now, we know that the female population became 1.25 times itself in 1990 from what it was in 1980.
Hence, the female population in 1980 = 200/1.25 = 160
Also, the female population became 1.2 times itself in 1980 from what it was in 1970.
Hence, the female population in 1970 = 160/1.2 = 1600/12 = 400/3
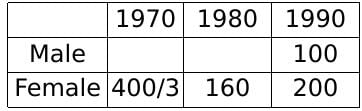
Let the male population in 1970 be x. Hence, the male population in 1980 is 1.4x.
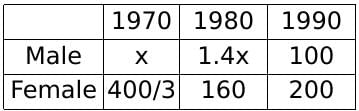
Now, the total population in 1980 = 1.25 times the total population in 1970.
Hence, 1.25 (x + 400/3) = 1.4x + 160
Hence, x = 400/9.
Population change = 300 - 400/9 - 400/3 = 300 - 1600/9 = 1100/9
percentage change = 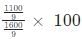
= 1100/16% = 68.75%
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:Consider a sequence of real numbers, x1,x2,x3,... such that xn+1 = xn + n − 1 for all n ≥ 1. If x1 = −1 then x100 is equal to
Explanation
Given xn+1 = xn + n − 1 and x1 = -1.
Considering
x1 = -1. (1)
x2 = x1 + 1 - 1 = x1 + 0 (2)
x3 = x2 + 2 - 1 = x2 + 1 (3)
x4 = x3 + 3 - 1 = x3 + 2 (4)
x100 = x99 + 98 (100)
Adding the LHS and RHS for the hundred equations we have:
(x1 + x2+......................x100) = (-1 + 0 +.........98) + (x1 + x2+...............x99)
Subtracting this we have :
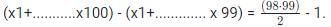
x100 = 4851 - 1 = 4850
Alternatively
x1 = −1
x2 = x1 + 1 − 1 = x1 = −1
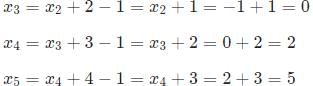
......
If we observe the series, it is a series that has a difference between the consecutive terms in an AP.
Such series are represented as t(n)=a + bn + cn2
We need to find t(100).
t(1) = -1
a + b + c = -1
t(2) = -1
a + 2b + 4c = -1
t(3) = 0
a + 3b + 9c = 0
Solving we get,
b + 3c = 0
b + 5c = 1
c = 0.5
b = -1.5
a = 0
Now,
t(100) = (−1.5)100 + (0.5)1002
= −150 + 5000 = 4850
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:The arithmetic mean of scores of 25 students in an examination is 50. Five of these students top the examination with the same score. If the scores of the other students are distinct integers with the lowest being 30, then the maximum possible score of the toppers is
Explanation
Let sum of marks of students be x
Now therefore x = 25 x 50 =1250
Now to maximize the marks of the toppers
We will minimize the marks of 20 students
so their scores will be (30,31,32.....49 )
let score of toppers be y
so we get 5y + 20/2 (79) = 1250
we get 5y + 790 = 1250
5y = 460
y = 92
So scores of toppers = 92
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:One part of a hostel’s monthly expenses is fixed, and the other part is proportional to the number of its boarders. The hostel collects ₹ 1600 per month from each boarder. When the number of boarders is 50, the profit of the hostel is ₹ 200 per boarder, and when the number of boarders is 75, the profit of the hostel is ₹ 250 per boarder. When the number of boarders is 80, the total profit of the hostel, in INR, will be
Explanation
Profit per boarder = Total profit / Number of boarders.
Let the number of boarders be n.
Profit/boarder = 1600 - (Total cost/n)
Let the total cost be a + bn, where a = fixed, and b is the variable additional cost per boarder.
Profit/boarder = 1600 - (a + bn)/n
Profit/boarder = 1600 - a/n - b
1600 - a/50 - b = 200
1600 - a/75 - b = 250
Solving, we get a = 7500, and b = 1250
Hence, total profit with 80 people = 80 ( 1600 - 7500/80 - 1250) = 80 (350 - 7500/80) = 28000 - 7500 = Rs. 20500
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is
Explanation
Let us draw the rectangle.

Now, definitely, three sides should be fenced at Rs 100/ft, and one side should be fenced at Rs 200/ft.
In this question, we are going to assume that the L is greater than B.
Hence, the one side painted at Rs 200/ft should be B to minimise costs.
Hence, the total cost = 200B + 100B + 100L + 100L = 300B + 200L
Now, L x B = 60000
B = 60000/L
Hence, total cost = 300B + 200L = 18000000/L + 200L
To minimise this cost, we can use AM > =GM,
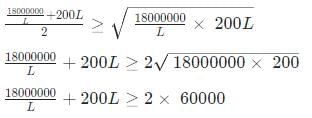
Hence, minimum cost = Rs 120000.
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is
Explanation
We can say 40m is the perimeter of the park
so side of rhombus = 10
Now 1/2 × d1× d2 = 96
so we get d1 × d2 = 192 (1)
And as we know diagonals of a rhombus are perpendicular bisectors of each other :
so 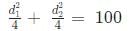
so we get d12+ d22 = 400 (2)
Solving (1) and (2)
We get d1 =12 and d2 = 16
Now the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is= (12+16)(125) =3500
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is
Explanation
Let price of smallest cup be 2x and medium be 5x and large be y
Now by condition 1
we get 2x × 5x × y = 800
we get x2y = 80 (1)
Now as per second condition ;
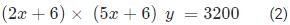
Now dividing (2) and (1)
We get
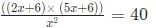
we get 10x2 + 42x + 36 = 40x2
we get 30x2 − 42x − 36 = 0
5x2 − 7x − 6= 0
we get x = 2
So 2x = 4 and 5x = 10
Now substituting in (1) we get y = 20
Now therefore sum = 4 + 10 + 20 =34
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:Mira and Amal walk along a circular track, starting from the same point at the same time. If they walk in the same direction, then in 45 minutes, Amal completes exactly 3 more rounds than Mira. If they walk in opposite directions, then they meet for the first time exactly after 3 minutes. The number of rounds Mira walks in one hour is
Explanation
Considering the distance travelled by Mira in one minute = M,
The distance traveled by Amal in one minute = A.
Given if they walk in the opposite direction it takes 3 minutes for both of them to meet. Hence 3 x (A + M) = C. (1)
C is the circumference of the circle.
Similarly, it is mentioned that if both of them walk in the same direction Amal completes 3 more rounds than Mira :
Hence 45*(A - M) = 3C. (2)
Multiplying (1)*15 we have :
45A + 45M = 15C.
45A - 45M = 3C.
Adding the two we have A = 18C/90
Subtracting the two M = 12C / 90
Since Mira travels 12C/90 in one minute, in one hour she travels : 12C/90 . 60 = 8C
Hence a total of 8 rounds.
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:If a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is
Explanation
Let the alloy contain x Kg silver and y kg copper
Now when mixed with 3Kg Pure silver
we get
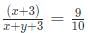
we get 10x + 30 = 9x + 9y + 27
9y - x = 3 (1)
Now as per condition 2
silver in 2nd alloy = 2(0.9) =1.8
so we get
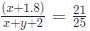
we get 21y - 4x = 3 (2)
solving (1) and (2) we get y= 0.6 and x = 2.4
so x + y = 3
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:If a triangle ABC, ∠BCA = 50o. D and E are points on AB and AC, respectively, such that AD = DE. If F is a point on BC such that BD = DF , then ∠FDE, in degrees, is equal to
Explanation
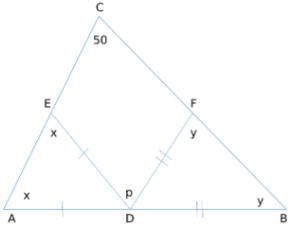
We need to find out p.
Angle ADE = 180 - 2x
Angle BDF = 180 - 2y
Now, 180 - 2y + p + 180 - 2x = 180 [Straight line = 180 deg]
p = 2x + 2y - 180
Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]
x + y = 130
p = 260 - 180 = 80 degrees.
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:Bank A offers 6% interest rate per annum compounded half-yearly. Bank B and Bank C offer simple interest but the annual interest rate offered by Bank C is twice that of Bank B. Raju invests a certain amount in Bank B for a certain period and Rupa invests ₹ 10,000 in Bank C for twice that period. The interest that would accrue to Raju during that period is equal to the interest that would have accrued had he invested the same amount in Bank A for one year. The interest accrued, in INR, to Rupa is
Explanation
Bank A: 6% p.a. 1/2 yearly (CI)
Bank B: x% p.a (SI)
Bank C: 2x% p.a (SI)
Let Raju invest Rs P in bank B for t years. Hence, Rupa invests Rs 10,000 in bank C for 2t years.
Now,

We need to calculate
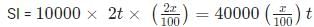
= 40000 × 0.0609 = 2436
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:If f(x) = x2 − 7x and g(x) = x + 3, then the minimum value of f(g(x))−3x is:
Explanation
Now we have :
f(g(x))−3x
so we get f(x + 3) - 3x
= (x + 3)2 − 7(x + 3) − 3x
= x2 - 4x - 12
Now minimum value of expression =
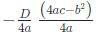
We get - (16 + 48)/4
= -16
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:Anil can paint a house in 12 days while Barun can paint it in 16 days. Anil, Barun, and Chandu undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chandu is paid in proportion to the work done by him, then the amount in INR received by him is
Explanation
Now Anil Paints in 12 Days
Barun paints in 16 Days
Now together Arun , Barun and Chandu painted in 6 Days
Now let total work be W
Now each worked for 6 days
So Anil's work = 0.5W
Barun's work = 6W/16 = 3W/8
Therefore Charu's work = W/2 - 3W/8 = W/8
Therefore proportion of charu = 24000/8 = 3,000
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:If n is a positive integer such that 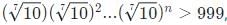 then the smallest value of n is
then the smallest value of n is
Explanation
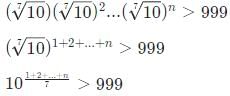
For minimum value of n,
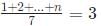
1 + 2 + ... + n = 21
We can see that if n = 6, 1 + 2 + 3 + ... + 6 = 21.
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
Explanation
The question asks for the number of 4 digit numbers using only the digits 1, 2, and 3 such that the digits 2 and 3 appear at least once.
The different possibilities include :
Case 1:The four digits are ( 2, 2, 2, 3). Since the number 2 is repeated 3 times. The total number of arrangements are : 4!/3! = 4.
Case 2: The four digits are 2, 2, 3, 3. The total number of four-digit numbers formed using this are : 4!/2!.2! = 6.
Case 3: The four digits are 2, 3, 3, 3. The number of possible 4 digit numbers are : 4!/3! = 4
Case4: The four digits are 2, 3, 3, 1. The number of possible 4 digit numbers are :
4!/2! = 12
Case 5: Using the digits 2, 2, 3, 1. The number of possible 4 digit numbers are :
4!/2! = 12
Case 6: Using the digits 2, 3, 1, 1. The number of possible 4 digit numbers are :
4!/2! = 12
A total of 12 + 12 + 12 + 4 + 6 + 4 = 50 possibilities.
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:Let ABCD be a parallelogram. The lengths of the side AD and the diogonal AC are 10cm and 20cm, respectively. If the angle ∠ADC is equal to 300 then the area of the parallelogram, in sq.cm is
Explanation
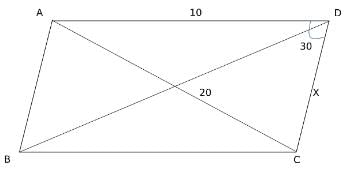
Applying cosine rule in triangle ACD,
100 + X2 − 2 × 10 × Xcos30 = 400

Solving, we get X
= 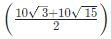
Hence, area = 10Xsin 30 = 
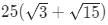
Report a problem
Question for Quant For CAT 2021 (Slot - 3)
Try yourself:If 3x + 2 ∣ y ∣ + y = 7 and x+ ∣ x ∣ + 3y = 1 then x + 2y is:
Explanation
We need to check for all regions:
x > = 0, y > = 0
x > = 0, y < 0
x < 0, y > = 0
x < 0, y < 0
However, once we find out the answer for any one of the regions, we do not need to calculate for other regions since the options suggest that there will be a single answer.
Let us start with x >= 0, y >= 0,
3x + 3y = 7
2x + 3y = 1
Hence, x = 6 and y = -11/3
Since y > = 0, this is not satisfying the set of rules.
Next, let us test x >= 0, y < 0,
3x - y = 7
2x + 3y = 1
Hence, y = -1
x = 2.
This satisfies both the conditions. Hence, this is the correct point.
We need the value of x + 2y
x + 2y = 2 + 2(-1) = 2 - 2 = 0.
Report a problem
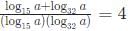 then a must lie in the range
then a must lie in the range
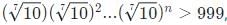 then the smallest value of n is
then the smallest value of n is