Directions: For the following questions answer them individually.
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Two alcohol solutions, A and B, are mixed in the proportion 1:3 by volume. The volume of the mixture is then doubled by adding solution A such that the resulting mixture has 72% alcohol. If solution A has 60% alcohol, then the percentage of alcohol in solution B is
Explanation
Initially let's consider A and B as one component
The volume of the mixture is doubled by adding A(60% alcohol) i.e they are mixed in 1:1 ratio and the resultant mixture has 72% alcohol.
Let the percentage of alcohol in component 1 be 'x'.
Using allegations ,
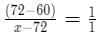
⇒ x = 84
Percentage of alcohol in A = 60% ⇒ Let's percentage of alcohol in B = x%
The resultant mixture has 84% alcohol. ratio = 1:3
Using allegations ,
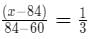
⇒ x = 92%
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:A batsman played n + 2 innings and got out on all occasions. His average score in these n + 2 innings was 29 runs and he scored 38 and 15 runs in the last two innings. The batsman scored less than 38 runs in each of the first n innings. In these n innings, his average score was 30 runs and lowest score was x runs. The smallest possible value of x is
Explanation
Given,
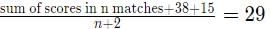
Given,
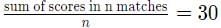
⇒ 30n + 53 = 29(n + 2) ⇒ n = 5
Sum of the scores in 5 matches = 29*7 - 38 - 15 = 150
Since the batsmen scored less than 38, in each of the first 5 innings. The value of x will be minimum when remaining four values are highest
⇒ 37 + 37 + 37 + 37 + x = 150
⇒ x = 2
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Let m and n be positive integers, x2 + mx + 2n = 0 and x2 + 2nx + m = 0 have real roots, then the smallest possible value of m+n is
Explanation
To have real roots the discriminant should be greater than or equal to 0.
So, 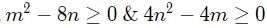
∴ 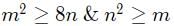
Since m,n are positive integers the value of m+n will be minimum
when m = 4 and n = 2.
∴ m + n=6.
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:A contractor agreed to construct a 6 km road in 200 days. He employed 140 persons for the work. After 60 days, he realized that only 1.5 km road has been completed. How many additional people would he need to employ in order to finish the work exactly on time?
Explanation
Let the desired efficiency of each worker '6x' per day.
140*6x*200 = 6 km ...(i)
In 60 days 60/200*6=1.8 km of work is to be done but actually 1.5km is only done.
Actual efficiency 'y' = 1.5/1.8 *6x = 5x.
Now, left over work = 4.5km which is to be done in 140 days with 'n' workers whose efficiency is 'y'.
⇒ n*5x*140=4.5 ...(ii)
(i) / (ii) gives,
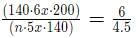
⇒ n = 180.
∴ Extra 180 - 140 = 40 workers are needed.
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:If x1 = −1 and xm = xm+1+(m+1) for every positive integer m, then X100 equals
Explanation
x1 = −1
x1 = x2 + 2 ⇒ x2 = x1 - 2 = -3
Similarly,
x3 = x1 - 5 = -6
x4 = -10
.
.
The series is -1, -3, -6, -10, -15......
When the differences are in AP, then the nth term is 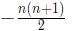
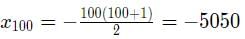
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:If loga30 = A,loga( 5/3) =−B and log2a= 1/3 , then log3a equals
Explanation
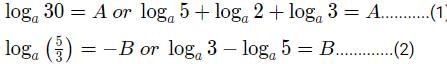
and finally loga 2 = 3
Substituting this in (1) we get loga 5+loga 3 = A − 3
Now we have two equations in two variables (1) and (2) . On solving we get
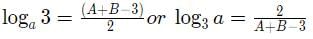
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Dick is thrice as old as Tom and Harry is twice as old as Dick. If Dick's age is 1 year less than the average age of all three, then Harry's age, in years, is
Explanation
Let tom's age = x
⇒ Dick = 3x
⇒ harry = 6x
Given,
3x + 1 = (x + 3x + 6x)/3
⇒ x = 3
Hence, Harry's age = 18 years
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Vimla starts for office every day at 9 am and reaches exactly on time if she drives at her usual speed of 40 km/hr. She is late by 6 minutes if she drives at 35 km/hr. One day, she covers two-thirds of her distance to office in one-thirds of her usual total time to reach office, and then stops for 8 minutes. The speed, in km/hr, at which she should drive the remaining distance to reach office exactly on time is
Explanation
Let distance = d
Given, 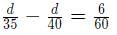
⇒ d = 28km
The actual time taken to travel 28km = 28/40 = 7/10 hours = 42 min.
Given time taken to travel 58/3 km = 1/3 *42 = 14 min.
Then a break of 8 min.
To reach on time, he should cover remaining 28/3 km in 20 min
⇒ Speed = 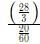
= 28 km/hr
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is
Explanation
Equation of circle x2 + y2 + 2gx + 2fy + c = 0
It passes through (0,0), (4,0) and (3,9). Substitute each point in the above equation:
⇒ On substituting the value (0,0) in the above equation, we obtain: c = 0
⇒ On substituting the value (4,0) in the above equation, we obtain:16 + 0 + 8g + 0 = 0 ; g = -2g = −2
⇒ On substituting the value (3,9) in the above equation, we obtain: 9 + 81 − 12 + 18f = 0 ; f = -13/3
Radius of the circle
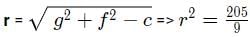
Therefore, Area = π r2
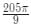
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Let m and n be natural numbers such that n is even and 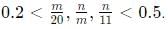 Then m − 2n equals
Then m − 2n equals
Explanation
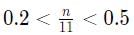
⇒ 2.2 < n < 5.5
Since n is an even natural number, the value of n = 4
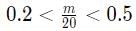
⇒ 4 < m < 10. Possible values of m = 5,6,7,8,9
Since 0.2 < n/m < 0.5, the only possible value of m is 9
Hence m - 2n = 9 - 8 = 1
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:How many integers in the set {100, 101, 102, ..., 999} have at least one digit repeated?
Explanation
Total number of numbers from 100 to 999 = 900
The number of three digits numbers with unique digits:
_ _ _
The hundredth's place can be filled in 9 ways ( Number 0 cannot be selected)
Ten's place can be filled in 9 ways
One's place can be filled in 8 ways
Total number of numbers = 9 * 9 * 8 = 648
Number of integers in the set {100, 101, 102, ..., 999} have at least one digit repeated = 900 - 648 = 252
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:In the final examination, Bishnu scored 52% and Asha scored 64%. The marks obtained by Bishnu is 23 less, and that by Asha is 34 more than the marks obtained by Ramesh. The marks obtained by Geeta, who scored 84%, is
Explanation
Let the total marks be 100x
Marks obtained by Bishnu = 52x
Marks obtained by Asha = 64x
Marks obtained by Ramesh = 52x + 23
Marks obtained by Ramesh = 64x - 34
⇒ 52x + 23 = 64x - 34
⇒ x = 19/4
Marks obtained by Geeta =84x = 84*19/4 = 399
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:If a,b,c are non-zero and 14a =36b =84c , then 6b( 1/c - 1/a) is equal to
Explanation
Let 14a =36b =84c = k
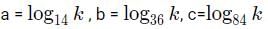
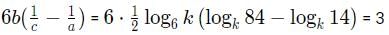
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:A person invested a certain amount of money at 10% annual interest, compounded half-yearly. After one and a half years, the interest and principal together became Rs.18522. The amount, in rupees, that the person had invested is
Explanation
Given,
Rate of interest = 10%
Since it is compounded half-yearly, R = 5%
n = 3
We know,
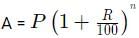
18522 = P(1 + 0.05)3
⇒ P = 16000
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:A man buys 35 kg of sugar and sets a marked price in order to make a 20% profit. He sells 5 kg at this price, and 15 kg at a 10% discount. Accidentally, 3 kg of sugar is wasted. He sells the remaining sugar by raising the marked price by p percent so as to make an overall profit of 15%. Then p is nearest to
Explanation
Let the cost price of 1kg of sugar = Rs 100
The total cost price of 35 kg = Rs3500
Marked up price per kg = Rs 120
GIven, the final profit is 15% ⇒ Final SP of 35 kg = 3500 *1.15 = Rs 4025
First 5 kg's are sold at 20% marked up price ⇒ SP1 = 5⋅100⋅1.2 = Rs 600
Next 15 kgs are sold after giving 10% discount ⇒ SP2 = 15⋅100⋅1.2⋅0.9 = 1620
3kgs of sugar got wasted
⇒ 23 kg of sugar was sold at Rs (600 +1620) = Rs 2220
Remaining 12kg should be sold at Rs 4025 - 2220 = Rs1805
⇒ SP of 1kg = 1805/12 ≃ 150
Hence, the seller should further mark up by 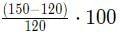
= 25%
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:The points (2,1) and (-3,-4) are opposite vertices of a parallelogram.If the other two vertices lie on the line x + 9y + c = 0, then c is
Explanation
The midpoints of two diagonals of a parallelogram are the same
Hence the midpoint of (2,1) and (-3,-4) lie on x + 9y + c = 0
midpoint of (2,1) and (-3,-4) = 
Keeping this cordinates in the above line equation, we get c = 14
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:A and B are two railway stations 90 km apart. A train leaves A at 9:00 am, heading towards B at a speed of 40 km/hr. Another train leaves B at 10:30 am, heading towards A at a speed of 20 km/hr. The trains meet each other at
Explanation
The distance travelled by A between 9:00 Am and 10:30 Am is 3/2*40 = 60 km.
Now they are separated by 30 km
Let the time taken to meet = t
Distance travelled by A in time t + Distance travelled by B in time t = 30
40t + 20t =30 ⇒ t = 1/2 hour
Hence they meet at 11:00 AM
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Let N, x and y be positive integers such that N = x + y,2 < x < 10 and 14 < y < 23. If N > 25, then how many distinct values are possible for N?
Explanation
Possible values of x = 3,4,5,6,7,8,9
When x = 3, there is no possible value of y
When x = 4, the possible values of y = 22
When x = 5, the possible values of y=21,22
When x = 6, the possible values of y = 20.21,22
When x = 7, the possible values of y = 19,20,21,22
When x = 8, the possible values of y = 18,19,20,21,22
When x = 9, the possible values of y = 17,18,19,20,21,22
The unique values of N = 26,27,28,29,30,31
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Let k be a constant. The equations kx + y = 3 and 4x + ky = 4 have a unique solution if and only if
Explanation
Two linear equations ax + by = c and dx + ey = f have a unique solution if a/d ≠ b/e.
Therefore k/4 ≠ 1/k ⇒ k2 ≠ 4
⇒ k ≠ |2|
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7?
Explanation
The number of multiples of 2 between 1 and 120 = 60
The number of multiples of 5 between 1 and 120 which are not multiples of 2 = 12
The number of multiples of 7 between 1 and 120 which are not multiples of 2 and 5 = 7
Hence, number of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7 = 120 - 60 - 12 - 7 = 41
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:How many pairs(a, b) of positive integers are there such that a ≤ b and ab = 42017?
Explanation
ab = 42017 = 24034
The total number of factors = 4035.
out of these 4035 factors, we can choose two numbers a,b such that a < b in [4035/2] = 2017.
And since the given number is a perfect square we have one set of two equal factors.
∴ many pairs(a, b) of positive integers are there such that a ≤ b and ab = 42017
= 2018.
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:Anil, Sunil, and Ravi run along a circular path of length 3 km, starting from the same point at the same time, and going in the clockwise direction. If they run at speeds of 15 km/hr, 10 km/hr, and 8 km/hr, respectively, how much distance in km will Ravi have run when Anil and Sunil meet again for the first time at the starting point?
Explanation
Anil and Sunil will meet at a first point after LCM (3/15, 3/10) = 3/5 hr
In the mean time, distance travelled by ravi = 8 x 3/5 = 4.8 km
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:n a trapezium ABCD, AB is parallel to DC, BC is perpendicular to DC and ∠BAD = 45o. If DC = 5cm, BC = 4 cm,the area of the trapezium in sq cm is
Explanation
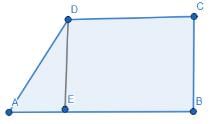
Given, BC = DE = 4
CD = BE = 5
In triangle ADE, EAD=45^{0}$$
tan 45 = DE/AE ⇒ AE = 4
Area of trapezium = Area of rectangle BCDE + Area of triangle AED
= 20 + 8 = 28
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:The area, in sq. units, enclosed by the lines x = 2,y = | x − 2| + 4, the X-axis and the Y-axis is equal to
Explanation
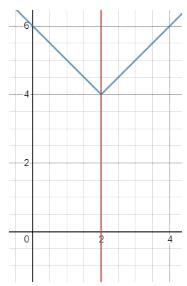
The required figure is a trapezium with vertices A(0,0), B(2,0), C(2,4) and D(0,6)
AB = 2 BC = 4 and AD = 6
Area of trapezium = 1/2 (sum of the opposite sides) . height = 1/2(4 + 6) . 2
= 10
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself:If f(x + y) = f(x)f(y) and f(5) = 4 f(5) = 4, then f(10) − f(−10) is equal to
Explanation
The given function is equivalent to f(x) = ax
Given, f(5) = 4
⇒ 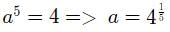
⇒ 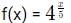
f(10) - f(-10) = 16 - 1/16 = 15.9375
Report a problem
Question for Quant For CAT 2020 (Slot - 3)
Try yourself: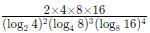 equals
equals
Explanation
Report a problem
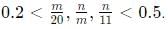 Then m − 2n equals
Then m − 2n equals
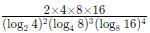 equals
equals
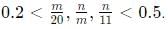 Then m − 2n equals
Then m − 2n equals
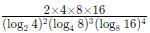 equals
equals