Squares and Square Roots Class 8 Notes Maths Chapter 5
| Table of contents |

|
| Introduction to Square Numbers |

|
| Properties of Square Numbers |

|
| Some More Interesting Patterns |

|
| Finding the Square of a Number |

|
| Square Roots |

|
| Square Roots of Decimals |

|
Introduction to Square Numbers
Imagine you have a collection of tiles, and you want to arrange them into a perfect square shape. If you arrange them so that each side of the square has the same number of tiles, you’ll end up with a special type of number called a square number.
What Are Square Numbers?
A square number is a number that you get when you multiply an integer by itself. For example:
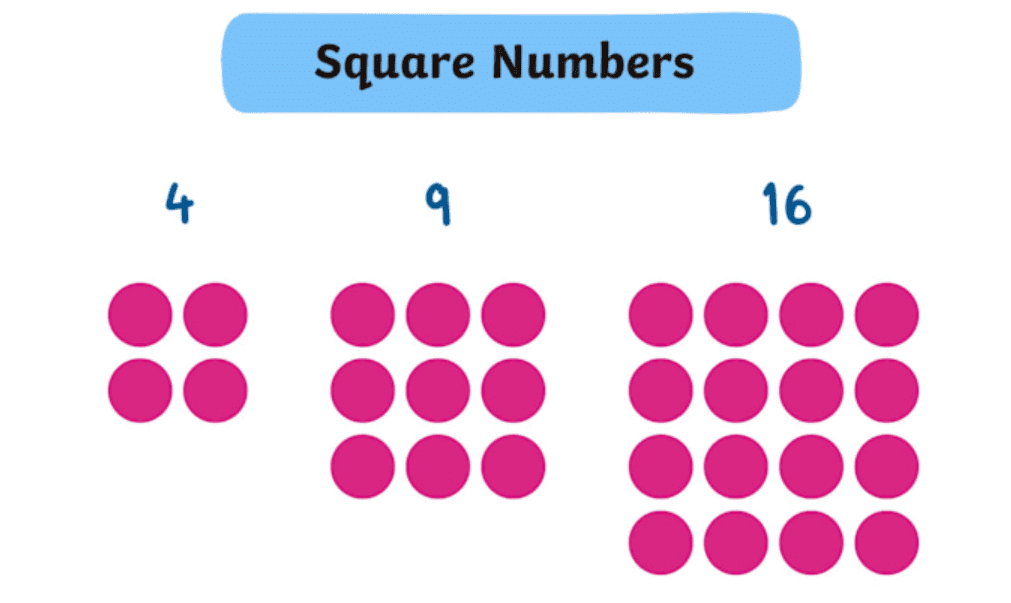
- If you take the number 2 and multiply it by itself (2 × 2), you get 4. So, 4 is a square number.
- If you take the number 3 and multiply it by itself (3 × 3), you get 9. So, 9 is a square number.
 Square Numbers
Square Numbers
In mathematical terms, we write this as:
- 22 = 4
- 33 = 9
Here, the little “2” above the number is called a square exponent or power. It simply tells us to multiply the number by itself.
Why Are They Called Square Numbers?
They’re called square numbers because if you draw a square with side lengths equal to the number, the total number of squares inside the larger square will be the square number. For instance:
- For 4 (which is 22), you can draw a 2 × 2 grid of squares, and there will be 4 small squares inside it.
- For 9 (which is 33), you can draw a 3 × 3 grid of squares, and there will be 9 small squares inside it.
Example Square of 5 is equal to 5×5=25
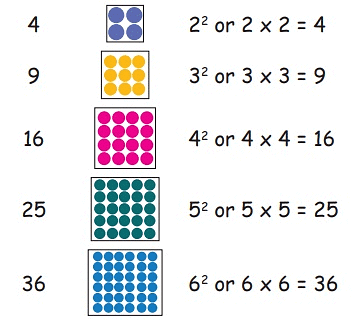 Square Numbers
Square Numbers
Properties of Square Numbers
- If a number has 0, 1, 4, 5, 6, or 9 in the unit’s place, then it may or may not be a square number.
Example: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 are square numbers. But 28 and 97 will not be perfect squares. - If a number has 1 or 9 in the unit’s place, then its square ends in 1.
Example: 112 = 121, 212 = 441, 192 = 361 and 292 = 841 - If a square number ends in 6, the number whose square it is will have either 4 or 6 in the unit’s place.
Example: 142 = 196, 162 = 256 and 242 = 576 - The unit digit of the square of any number will be the unit digit of the square of its last digit.
Example: The square of 23 is 529
232 = 529
The unit place of 23 has 3, and unit place of 529 has 9
A square of 3 is equal to 9 - The square root of a perfect square is always a natural number.
Example: √4 = 2, √9 = 3, √16 = 4 and √25 = 5 - Perfect squares will end with even numbers of zeros.
Example: 2500 is a perfect square, 100 is a perfect square. But 80 is not a perfect square, and 4000 is also not a perfect square. - Square of even numbers are always even.
Example: A Square of 2 is 4, and a Square of 6 is 36 - Square of odd numbers are always odd.
Example: Square of 7 is 49, and Square of 9 is 81
How to Find the square of a number with the unit’s place 5?
To find the square of a number with the unit's place as 5, we can follow these steps:
Step 1. Separate the number into two parts - the last digit (5) and the remaining part (N). Hence the number becomes N5.
Step 2. Multiply N with N+1. Multiply the product with 100.
Step 3. Add 25 at the end of the result obtained in step 2.
Examples:
Square of 15 : Here N = 1,
Then 152=(1×2)×100+25=200+25=225
Square of 205
Here N= 20,
Then 2052=(20×21)×100+25=42000+25=42025
Some More Interesting Patterns
There exist interesting patterns in:
- Adding triangular numbers
- Numbers between square numbers
- Adding odd numbers
- A sum of consecutive natural numbers
- Product of two consecutive even or odd natural numbers
1. Adding Triangular Numbers
Triangular numbers: Triangular numbers are a sequence created by adding natural numbers continuously. They form a triangular shape when arranged in dots. For example: 1, 3, 6, 10, 15, etc.
1
1+2=3
1+2+3=6
1+2+3+4=10
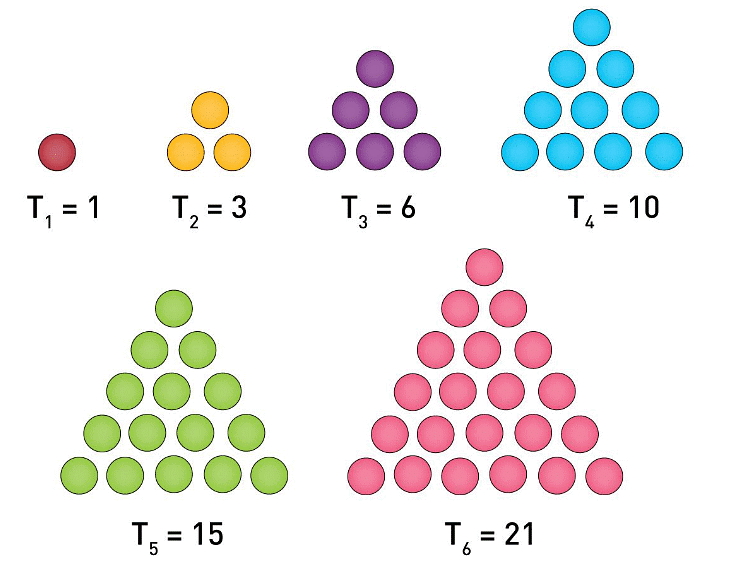 Diagram:
Diagram:
•
••
•••
Now, if we add two consecutive triangular numbers, we get a square number.
Example : 1+3=4=22 and 3+6=9=32.
2. Numbers between Square Numbers
Numbers between square numbers are the integers that fall between two perfect squares.
There are 2n non-perfect square numbers between squares of the numbers n and (n + 1), where n is any natural number.
Example:
There are two non-perfect square numbers (2, 3) between 12=1 and 22=4.
There are four non-perfect square numbers (5, 6, 7, 8) between 22= 4 and 32=9.
3. Adding Odd Numbers
The sum of first n odd natural numbers is n2.
Example:
1 = 12 [one odd number]
1 + 3 =4 = 22 [sum of first two odd numbers]
1 + 3 + 5 = 9 = 32 [sum of first three odd numbers]
1 + 3 + 5 + 7 = 16 = 42 [sum of first four odd numbers]
4. A sum of consecutive natural numbers
The sum of two consecutive numbers is always an odd number. For example, consider a consecutive number sequence 1, 2, 3, 4, 5, 6, 7, 8, 9.
Here, the sum of the two consecutive numbers will always be an odd number. 1+2 = 3, 2+3 = 5, 3+4 = 7, and so on.
The square of an odd number n can be expressed as the sum of two consecutive positive integers
The fractions are as follows:
(n² - 1)2 and (n² + 1)2.
For example: 3²9 = 4 + 5 = (3² - 1)2 + (3² + 1)2.
Similarly: 5²25 = 12 + 13 = (5² - 1)2 + (5² + 1)2.
5. Product of Two Consecutive Even or Odd Natural Numbers
The product of two even or odd natural number can be calculated as, (a+1)×(a−1)=(a2−1), where a is a natural number, and a−1, a+1, are the consecutive odd or even numbers.
For example:
11 and 13 are two odd consecutive numbers, therefore the multiplication of 11 and 13 can be calculated as:
11×13 = (12−1)×(12+1) = 122−1 = 144−1 = 143
6. Some more patterns in square numbers
Patterns in numbers like 1, 11, 111, … :
12= 1
112= 1 2 1
1112= 1 2 3 2 1
11112= 1 2 3 4 3 2 1
111112= 1 2 3 4 5 4 3 2 1
111111112=1 2 3 4 5 6 7 8 7 6 5 4 3 2 1
Patterns in numbers like 6, 67, 667, … :
72= 49
672= 4489
6672= 444889
66672= 44448889
666672= 4444488889
6666672= 444444888889
Finding the Square of a Number
To find the square of a number, you can use the concept of expanding the expression.
1. Let's take the example of finding the square of 23:
232 = (20 + 3)2 = (20 + 3) (20 + 3)
Expanding this expression, we get: 20 (20 + 3) + 3 (20 + 3)
Simplifying further: 20 x 20 + 20 x 3 + 3 x 20 + 3 x3
Calculating the multiplication: 400 + 60 + 60 + 9
Finally, adding up the values: 529
Therefore, the square of 23 is 529.
2. Let's find the square of 15 using the same method:
152 = (10 + 5)2 = (10 + 5) (10 + 5)
Expanding this expression: 10 (10 + 5) + 5 (10 + 5)
Simplifying further: 10 x10 + 10 x 5 + 5 x10 + 5 x 5
Calculating the multiplication: 100 + 50 + 50 + 25
Finally, adding up the values: 225
Therefore, the square of 15 is 225
Other patterns in squares
Let's explore other patterns in squares using the given examples:
When we look at the numbers and their corresponding squares, we can observe the following pattern:
- 252 = 625 = (2 × 3) hundreds + 25
- 352 = 1225 = (3 × 4) hundreds + 25
- 752 = 5625 = (7 × 8) hundreds + 25
- 1252 = 15625 = (12 × 13) hundreds + 25
In each case, we notice that the square can be expressed as a product of two consecutive numbers, followed by the word "hundreds," and then we add 25 at the end.
This pattern can be generalized as follows:
For any number n, where n is a positive integer:
n2 = (n × (n+1)) hundreds + 25
For example:
152 = 225 = (1 × 2) hundreds + 25
202 = 400 = (2 × 3) hundreds + 25
302 = 900 = (3 × 4) hundreds + 25
By following this pattern, we can easily find the squares of various numbers by multiplying two consecutive numbers, adding "hundreds," and then adding 25 at the end.
Pythagorean Triplets
A Pythagorean triplet is a set of three positive integers a, b, and c that satisfy the Pythagorean theorem, which states that the sum of the squares of the two smaller numbers is equal to the square of the largest number. In other words, a² + b² = c².

In the given formula for generating Pythagorean triplets, we have:
a = 2m
b = (m² - 1)
c = (m² + 1)
For any natural number m > 1, these three numbers form a Pythagorean triplet.
This is because (2m)² + (m² - 1)² = (m² + 1)², as stated in the formula.
Example :
Let's say m = 3, then
a = 2m = 2(3) = 6
b = (m² - 1) = (3² - 1) = (9 - 1) = 8
c = (m² + 1) = (3² + 1) = (9 + 1) = 10
We have the triplet (6, 8, 10). Now, let's check that it satisfies the Pythagorean theorem:
6² + 8² = 36 + 64 = 100
10² = 100
Square Roots
Determining the number whose square is already known is called finding the square root.
Square roots are the opposite of square numbers. They help us find the original number that was squared to get a particular square number.
Example:
12=1, square root of 1 is 1.
22=4, square root of 4 is 2.
32=9, square root of 9 is 3.
Finding Square Roots
Finding the square root of 180:
- Since: 100 < 180 < 225
- i.e. 10 < √180 < 15
- It is not very close, so we need to narrow down the range.
- Also, 132 = 169 < 180 and 142 = 196 > 180
- 13 < √180 < 14
- 196 is much closer to 180 than 169.
- Therefore, √180 is approximately equal to 14.
1. Finding square root through repeated subtraction
To find the square root of a number through repeated subtraction, follow these steps:
Step 1: Start with the given number (let's call it n) for which you want to find the square root.
Step 2: Begin subtracting successive odd numbers, starting from 1. Keep track of how many odd numbers you have subtracted.
Step 3: Continue subtracting the next odd number in the sequence until the result of the subtraction is zero.
Step 4: The number of odd numbers you subtracted in the process is the square root of the given number.
Example :
Suppose you want to find the square root of 49.
1. Start with the given number: n = 49
2. Begin subtracting successive odd numbers:
49 - 1 = 48 (1 odd number subtracted)
48 - 3 = 45 (2 odd numbers subtracted)
45 - 5 = 40 (3 odd numbers subtracted)
40 - 7 = 33 (4 odd numbers subtracted)
33 - 9 = 24 (5 odd numbers subtracted)
24 - 11 = 13 (6 odd numbers subtracted)
13 - 13 = 0 (7 odd numbers subtracted)
3, The result is zero after subtracting 7 odd numbers.
4. The square root of 49 is 7.
2. Finding square root through prime factorization
Prime factorization is the process of breaking down a composite number into its prime factors. Prime numbers are numbers greater than 1 that have no divisors other than 1 and themselves (e.g., 2, 3, 5, 7). Every composite number can be expressed as a product of prime numbers. Consider the prime factorization of various numbers and their squares:
- 6 = 2 × 3
36 = 2 × 2 × 3 × 3 - 8 = 2 × 2 × 2
64 = 2 × 2 × 2 × 2 × 2 × 2 - 12 = 2 × 2 × 3
144 = 2 × 2 × 2 × 2 × 3 × 3 - 15 = 3 × 5
225 = 3 × 3 × 5 × 5
We observe that each prime factor in the prime factorization of the square of a number occurs twice the number of times it occurs in the prime factorization of the original number.
By using this pattern, we can find the square root of a given square number. For example, let's find the square root of 324:
- The prime factorization of 324 is 2 × 2 × 3 × 3 × 3 × 3.
- Pairing the prime factors, we have 324 = (2 × 3 × 3) × (2 × 3 × 3) = (2 × 3 × 3)².
- Therefore, the square root of 324 is 2 × 3 × 3 = 18.
Similarly, we can find the square root of 256:
- The prime factorization of 256 is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
- Pairing the prime factors, we have 256 = (2 × 2 × 2 × 2) × (2 × 2 × 2 × 2) = (2 × 2 × 2 × 2)².
- Therefore, the square root of 256 is 2 × 2 × 2 × 2 = 16.
If we encounter a number that is not a perfect square, like 48, we can determine the smallest multiple of 48 which is a perfect square by completing the pairs of prime factors. In this case, multiplying 48 by 3 gives 144, which is a perfect square.
To find a number by which we should divide 48 to get a perfect square, we look for the factor that doesn't have a pair in the prime factorization. In this case, the factor 3 is not paired, so dividing 48 by 3 gives us 16, which is a perfect square.
3. Finding Square Root by Long Division Method
To find the square root using the long division method, follow these steps:
Let's find the square root of 484 by long division method:
Step 1: Place a bar over every pair of numbers starting from the digit at unit place. If the number of digits in it is odd, then the left-most single-digit too will have a bar.
Step 2: Take the largest number as a divisor whose square is less than or equal to the number on the extreme left. Divide and write quotient.
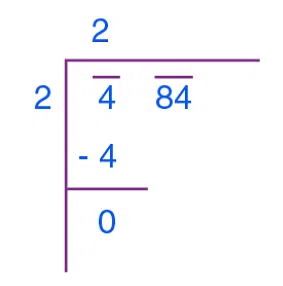
Step 3: Bring down the number which is under the next bar to the right side of the remainder.
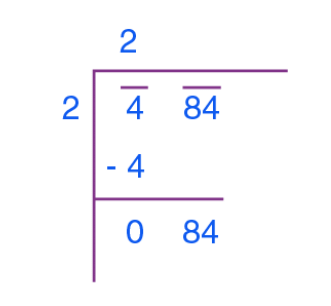 Step 4: Double the value of the quotient and enter it with a blank on the right side.
Step 4: Double the value of the quotient and enter it with a blank on the right side.
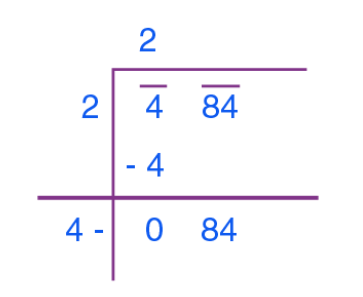
Step 5: Guess the largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
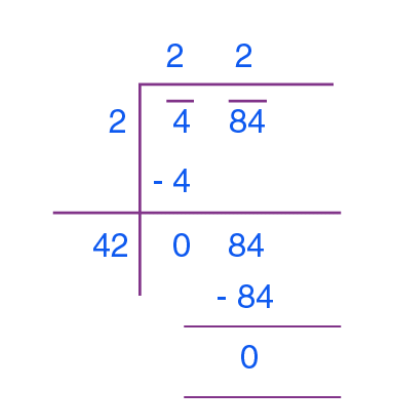
The remainder is 0, therefore, √484=22.
Square Roots of Decimals
Step 1: To find the square root of a decimal number we put bars on the integral part (i.e., 17) of the number in the usual manner. Place bars on the decimal part (i.e., 64) on every pair of digits beginning with the first decimal place. Proceed as usual. We get bar17.64
Step 2: Now proceed in a similar manner. The leftmost bar is on 17 and 42 < 17 < 52
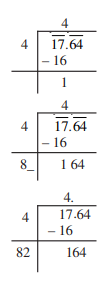
Step 3: Take this number as the divisor and the number under the left-most bar as the
dividend, i.e., 17. Divide and get the remainder.
Step 4: Double the divisor and enter it with a blank on its right. Since 64 is the decimal part so put a decimal point in the quotient.
Step 5: We know 82 × 2 = 164, therefore, the new digit is 2. Divide and get the remainder
Step 6: Since the remainder is 0 and no bar left, therefore square root of 17.64 is 4.2
|
81 videos|415 docs|31 tests
|
FAQs on Squares and Square Roots Class 8 Notes Maths Chapter 5
| 1. What are square numbers and how are they formed? |  |
| 2. What are some properties of square numbers? |  |
| 3. How do you find the square of a number? |  |
| 4. What is the process to calculate square roots? |  |
| 5. How do you find square roots of decimal numbers? |  |

















