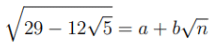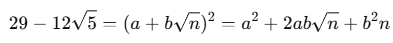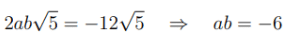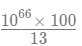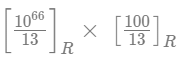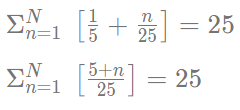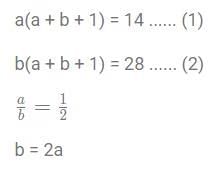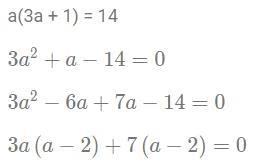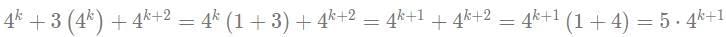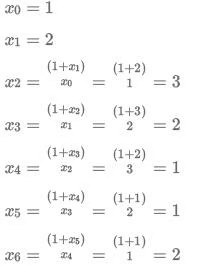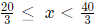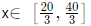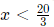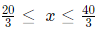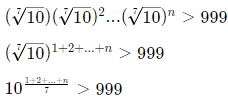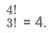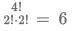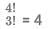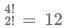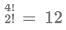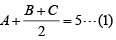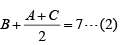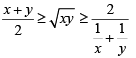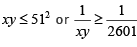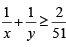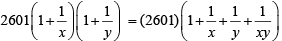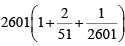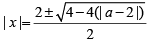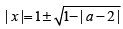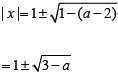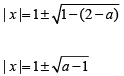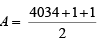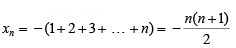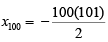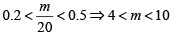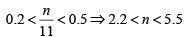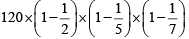Daily Practice Questions CAT Previous Year Questions with Answer PDF
2024
Q1: The sum of all four-digit numbers that can be formed with the distinct non-zero digits a, b, c and d, with each digit appearing exactly once in every number, is 153310 + n, where n is a single digit natural number. Then, the value of (a + b + c + d + n) is
Ans: 31
Sol:
Q2: When 10100 is divided by 7, the remainder is
(a) 3
(b) 6
(c) 1
(d) 4
Ans: d
Sol:
Q3: If m and n are natural numbers such that n > 1, and m = 225 × 340, then m - n equals [2024]
(a) 209942
(b) 209947
(c) 209932
(d) 209937
Ans: (b)
Sol: Given, mn = 225 × 340
We have to write the R.H.S. in a manner so that everything has the same power:
So, for that, we have to find the common factor of 25 and 40 which is 5.
So, mn = 225 × 340 can be written as (25)5 × (35)5 = (32 × 81 × 81)5 = (209952)5
So, the value of (m – n) = 209952 - 5 = 209947
Hence, option B is the correct answer.
Q4: When 3333 is divided by 11, the remainder is [2024]
(a) 5
(b) 6
(c) 1
(d) 10
Ans: (a)
Sol: 3333 can be written as 33 × 3330 = 27 × (243)66
When (243)66 divided by 11 it gives 1 as remainder and when 27 is divided by 11 it gives 5 as remainder
Hence, the required remainder = 1 × 5 = 5
Q5: The number of all positive integers up to 500 with non-repeating digits is
Ans: 378
Sol: Case 1-> 1-digit number = 9
Case 2-> 2-digit numbers = 9*9 = 81
Case 3-> 3-digit numbers = 4* 9* 8 = 288
Total number of positive integers upto 500 with non-repeating digits = 9 + 81 + 288 = 378
Hence, 378 is the required answer.
Q6: If 1068 is divided by 13, the remainder is
(a) 9
(b) 8
(c) 4
(d) 5
Ans: a
Sol: Now,
101 mod 13 = 10
102 mod 13 = 9
103 mod 13 = 12
104 mod 13 = 3
105 mod 13 = 4
106 mod 13 = 1
Now, 1068 mod 13 = 1066 * 102 mod 13 = 102 mod 13 = 9
Hence, 9 is the required answer.
Q7: If (a + b √n) is the positive square root of ( 29 − 12 √5), where a and b are integers, and n is a natural number, then the maximum possible value of (a + b + n ) is [2024]
Ans: 18
Sol: We are given that:
Squaring both sides:
Equating the rational and irrational parts:
- a2 + b2n = 29 (rational part) - 2ab√n =- 12√5 (irrational part)
From 2ab√n =- 12√5, comparing the terms under the square root gives n = 5, so:
Now, using a2 + b2n = 29, we substitute n = 5:
a2 + 5b2 = 29
We have two equations: 1. ab =- 6 2. a2 +5b2 = 29
By trial and error or systematic solving, we find a = 3, b = -2, and n = 5.
Thus, a + b + n = 3 - 2 + 5 = 6.
Q8: Suppose x1, x2, x3,…, x100 are in arithmetic progression such that x5 = −4 and 2x6 + 2x9 = x11 + x13 . Then, x100 equals [2024]
Sol: Let the first term of the arithmetic progression be a and the common difference be d.
Thus:
Xn = a + (n - 1)d
From the given conditions:
X5 = a + 4 d = −4
2X6 + 2X9 = X11 + X13
Using the formula for terms:
X6 = a + 5d
X9 = a + 8d
X11 = a + 10d
X13 = a + 12d
Substitute into the equation:
2(a + 5d) + 2(a + 8d) = (a + 10d) + (a + 12d)
Simplifying:
2a + 10d + 2a + 16d = 2a + 22d
4a + 26d = 2a + 22d
2a + 4d = 0 ⇒ a = −2d
Substitute a = − 2d into X5 =−4:
−2d + 4d = −4
2d = −4 ⇒ d = −2
Now, find X100:
X100 = a + 99d=−2(−2) + 99(−2) = 4 − 198 = −194
Q9: The sum of all real values of k for which the equation x2276 = x2276 holds true is k = 1, 32768, then the value of k is [2024]
Sol: The given equation is: x2276 = x2276
This is trivially true for any value of x. We are tasked with finding the values of k that satisfy this condition. Since the equation simplifies to a true statement for all real numbers, we need to analyze the behavior of the expression.
The key is to analyze the role of k in this expression.
After solving for the bounds of k, we find that:
k = -2/3
Thus, the real value of k is -2/3.
Q10: For any natural number n, let an be the largest integer not exceeding √n. Then the value of a1 + a2 + . . . + a50 is [2024]
Sol: We are asked to find the sum of a1 + a2 + . . . + a50, where an = [√n].
The value of an is the greatest integer less than or equal to √n.
To find the sum, we can break the sum into intervals where [√n] remains constant.
The value of [√n] will stay constant for values of n within certain intervals.
For n = 1 to 3, [√n] = 1 (3 terms). - For n = 4 to 8, [√n] = 2 (5 terms).
For n = 9 to 15, [√n] = 3 (7 terms). - For n = 16 to 24, [√n] = 4 (9 terms).
For n = 25 to 35, [√n] = 5 (11 terms). - For n = 36 to 48, [√n] = 6 (13 terms).
For n = 49 and 50, [√n] = 7 (2 terms).
Now, calculate the total sum:
Total sum=1 × 3 + 2 × 5 + 3 × 7 + 4 × 9 + 5 × 11 + 6 × 13 + 7 × 2
= 3 + 10 + 21 + 36 + 55 + 78 + 14 = 217.
Thus, the value of a1 + a2 + . . . + a50 = 217.
Q11: When 10100 is divided by 7, the remainder is [2024]
Sol: We are asked to find the remainder when 10100 is divided by 7.
This is equivalent to finding 10100 mod 7.
By Fermat's Little Theorem, since 7 is prime:
106 = 1 mod 7
So, we can reduce 10100 mod 7 by dividing 100 by 6 (since the powers of 10 repeat every 6 terms modulo 7):
100 ÷ 6 = 16 remainder 4
Thus:
10100 = 104 mod 7
Now calculate 104 mod 7:
104 = 10000 ⇒ 10000 ÷ 7=1428 remainder 4
Thus, the remainder when 10100 is divided by 7 is 4.
Q12: If (a + b √3)2 = 52 + 30√3, where a and b are natural numbers, then a + b equals [2024]
(a) 7
(b) 8
(c) 9
(d) 10
Ans: (b)
Sol: Opening the square on the left-hand side, we get a2 + 3b2 + 2ab√3
Comparing the rational part on both sides we get: a2 + 3b2= 52
And comparing the irrational part we get: 2ab√3 = 30√3
ab = 15, Since we are given that a and b are natural numbers, the possible values of a and b are (1, 15), (3, 5), (5, 3), or (15,1)
Putting these values in the first relation we got, we see that 15 squared would exceed the required value and would not be the case.
We need not check if a=5, b=3 or a=3, b=5 since the answer would be the same.
(a=5 and b=3 would satisfy it)
a + b = 5 + 3 = 8
Therefore, Option B is the correct answer.
Q13: If 1068 is divided by 13, the remainder is: [2024]
(a) 5
(b) 8
(c) 9
(d) 4
Ans: (c)
Sol: There are multiple ways of solving such questions involving remainders; one easy way is to look for a power of numerator that leaves a remainder of 1 or 01 when divided by the denominator.
In this instance, 1000, when divided by 13, leaves a remainder of -1
We can rewrite the numerator asThe remainder would be
(−1)22 × 9
Therefore, Option C is the correct answer.
2023
Q1: Let n be the least positive integer such that 168 is a factor of 1134n. If m is the least positive integer such that 1134n is a factor of 168m, then m + n equals [2023]
(a) 12
(b) 9
(c) 15
(d) 24
Ans: (c)
Sol: The prime factorizations of 168 and 1134 are as follows:
168 = 23 × 3 × 7
1134 = 2 × 34 × 7
Clearly, the smallest positive integral value of n, such that 168 is a factor of 1134n is 3.
1134n = 11343 = 23 × 312 × 73
Clearly, the smallest positive integral value of m, such that 11343 is a factor of 168m is 12.
Therefore, m + n = 12 + 3 = 15
Q2: The number of all natural numbers up to 1000 with non-repeating digits is [2023]
(a) 585
(b) 504
(c) 648
(d) 738
Ans: (d)
Sol: Single digit numbers with non-repeating digits = 9
(The unit’s digit is non-zero)
Two digit numbers with non-repeating digits = 9 × 9
(The tenth’s digit is non-zero and the unit digit can be any digit except the tenth’s digit.)
Three digit numbers with non-repeating digits = 9 × 9 × 8
(The hundred’s digit is non-zero and the tenth’s digit can be any digit except the hundred’s digit and the unit digit can be any digit except the tenth’s digit.)
So, totally there are (9 + 9 × 9 + 9 × 9 × 8) = 738 natural numbers up to 1000 with non-repeating digits.
Q3: For any natural numbers m, n , and k, such that k divides both m + 2n and 3m + 4n, k must be a common divisor of [2023]
(a) 2m and 3n
(b) m and 2n
(c) 2m and n
(d) m and n
Ans: (b)
Sol: k divides m + 2n
So, k also divides 2(m + 2n) = 2m + 4n
It is given that k divides 3m + 4n
Which means, k should also divide (3m + 4n) – (2m + 4n)
∴ k divides m
Since k divides m and m + 2n
k should also divide (m + 2n) – m = 2n
Therefore, k divides m and 2n.
Q4: The number of positive integers less than 50, having exactly two distinct factors other than 1 and itself, is [2023]
Sol: A positive integer less than 50, having exactly two distinct factors other than 1 and itself, is either a perfect cube below 50 or an integer that is a product of exactly two distinct primes.
Case i)
Perfect cubes below 50 are 23 and 33. So, two numbers here
Case ii)
For the product of two primes to be below 50, the individual primes should be below 25.
(Because, the smallest prime is 2 and multiplying 2 with anything greater than or equal to 25 yields a number greater than or equal to 50.)
2, 3, 5, 7, 11, 13, 17, 19, 23 are prime numbers less than 25.
2, 3, 5, 7 are the primes less than √50 any product of two numbers among them yields a product less than 50.
So, there are 4C2 = 6 pairs here.
11, 13, 17, 19, 23 are the primes greater than √50, any product of two numbers among them yields a product greater than 50.
So, there are 0 pairs here.
Between the two lists 11 and 13 can pair with 2 and 3, while 17, 19, and 23 can only pair with 2.
So, there are 7 pairs here.
So, totally, there are 2 + 6 + 0 + 7 = 15 such numbers.
Q5: The price of a precious stone is directly proportional to the square of its weight. Sita has a precious stone weighing 18 units. If she breaks it into four pieces with each piece having distinct integer weight, then the difference between the highest and lowest possible values of the total price of the four pieces will be 288000. Then, the price of the original precious stone is
(a) 1296000
(b) 1944000
(c) 972000
(d) 1620000
Ans: a
Sol: The price of a precious stone is directly proportional to the square of its weight.”
If W is the weight of the stone and P is the price of that stone, then P = k × W2
For the entire, unbroken stone, the price will be 182 × k = 324 k.
“If she breaks it into four pieces with each piece having distinct integer weight, then the difference between the highest and lowest possible values of the total price of the four pieces will be 288000.”
The minimum profit is achieved when the weights of the broken stones are close to each other, that is, the weights are 3, 4, 5, and 6 units.
In this case the combines worth of the four stones =(32 + 42 + 52 + 62)k = 86k
The maximum profit is achieved when the weights of the broken stones are far from each other, that is, the weights are 1, 2, 3, and 12 units.
In this case the combines worth of the four stones =(12 + 22 + 32 + 122)k = 158k
The difference in the total value = 2,88,000.
158k – 86k = 72k = 2,88,000
k = 4,000
So, the price of the original stone = 324 k = 12,96,000
Q6: Let a, b, m and n be natural numbers such that a > 1 and b > 1. If ambn = 144145, then the largest possible value of n - m is
(a) 580
(b) 290
(c) 579
(d) 289
Ans: c
Sol:
2022
Q1: For any real number x, let |x| be the largest integer less than or equal to x. If 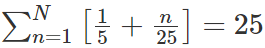 then N is [2022]
then N is [2022]
Sol: It is given,
For n = 1 to n = 19, value of function is zero.
For n = 20 to n = 44, value of function will be 1.
44 = 20 + n - 1
n = 25 which is equal to given value.
This implies N = 44
Q2: A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is
Sol: Let the number of 100 cheques, 250 cheques and 500 cheques be x, y and z respectively.
We need to find the maximum value of z.
x + y + z = 100 ...... (1)
100x + 250y + 500z = 15250
2x + 5y + 10z = 305 ...... (2)
2x + 2y + 2z = 200 ....... (1)
(2) - (1), we get
3y + 8z = 105
At z = 12, x = 3
Therefore, maximum value z can take is 12.
Q3: Let a and b be natural numbers. If a2 + ab + a = 14 and b2 + ab + b = 28, then (2a + b) equals
(a) 10
(b) 7
(c) 8
(d) 9
Ans: c
Sol:Substituting in (1), we get
Given, a and b are natural numbers.
Therefore, a = 2 and b = 4
2a + b = 2(2) + 4 = 8
The answer is option C.
Q4: For natural numbers x,y, and z, if xy + yz = 19 and yz + xz = 51, then the minimum possible value of xyz is
Ans: 34
Sol: It is given, y(x + z) = 19
y cannot be 19.
If y = 19, x + z = 1 which is not possible when both x and z are natural numbers.
Therefore, y = 1 and x + z = 19
It is given, z(x + y) = 51
z can take values 3 and 17Case 1:
If z = 3, y = 1 and x = 16
xyz = 3*1*16 = 48Case 2:
If z = 17, y = 1 and x = 2
xyz = 17*1*2 = 34
Minimum value xyz can take is 34.
Q5: Let A be the largest positive integer that divides all the numbers of the form 3k + 4k + 5k and B be the largest positive integer that divides all the numbers of the form 4k + 3(4k) + 4k+2, where k is any positive integer. Then (A + B) equals
Ans: 82
Sol: A is the HCF of 3k + 4k + 5k for different values of k.
For k = 1, value is 12
For k = 2, value is 50
For k = 3, value is 216
HCF is 2. Therefore, A = 2
HCF of the values is when k = 1, i.e. 5*16 = 80
Therefore, B = 80
A + B = 82
Q6: For some natural number n, assume that (15,000)! is divisible by (n!)!. The largest possible value of n is
(a) 4
(b) 5
(c) 6
(d) 7
Ans: d
Sol:
15000! = 15000 x 14999 x 14998 x …….. – (i)
From the options, the largest value is 7. We will check for that.
7! = 5040
5040! = 5040 x 5039 x ….. – (ii)
And (i) will definitely have (ii) as its multiple.
So, 7 is the answer.
Q7: The number of integer solutions of the equation 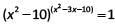 is
is
Ans: 4
Sol:
(x2 – 10)(x^2 – 3x – 10) = 1
In questions of the form ab = 1, there are basically 3 cases
i. (anything)0 = 1
ii. 1anything = 1
iii. (-1)even = 1
For (i), x2 – 3x – 10 = 0
=> x = -2, 5
For (ii), x2 = 10 but here the value of x won’t be an integer.
For (iii), x = ±3 and for both these values we get the power’s value as even.
Total 4 integer solutions.
Q8: The arithmetic mean of all the distinct numbers that can be obtained by rearranging the digits in 1421, including itself, is
(a) 3333
(b) 2442
(c) 2222
(d) 2592
Ans: c
Sol:
We will solve this like we used to do basic addition in childhood
For eg.
Number of distinct numbers that we will add = 4!/2! = 12
Each digit will repeat 12/4 = 3 times
3(1+1+2+4) = 24
24 will be the sum of each of the 4 columns
Sum = 26664
Average = 26664/12 = 2222
2021
Q1: How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order? [2021]
Ans: 70
Sol: Let the numbers be of the form 100a + 10b + c, where a, b, and c represent single digits.
Then (100c + 10b + a) - (100a+ 10b + c) = 198
99c - 99a = 198
c - a = 2.
Now, a can take the values 1-7. a cannot be zero as the initial number has 3 digits and cannot be 8 or 9 as then c would not be a single-digit number.
Thus, there can be 7 cases.
B can take the value of any digit from 0-9, as it does not affect the answer. Hence, the total cases will be 7× 10 = 70.
Q2: If 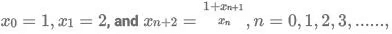 then x2021 is equal to
then x2021 is equal to
(a) 4
(b) 1
(c) 3
(d) 2
Ans: d
Sol:Hence, the series begins to repeat itself after every 5 terms. Terms whose number is of the form 5n are 1, 5n+1 are 2... and so on, where n=0,1,2,3,....
2021 is of the form 5n+1. Hence, its value will be 2.
Q3: For all possible integers n satisfying 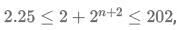 then the number of integer values of
then the number of integer values of 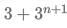 is:
is:
Ans: 7
Sol:If we see the second expression that is provided, i.e
3 + 3n+1, it can be implied that n should be at least -1 for this expression to be an integer.
So, n = -1, 0, 1, 2, 3, 4, 5.
Hence, there are a total of 7 values.
Q4: For a 4-digit number, the sum of its digits in the thousands, hundreds and tens places is 14, the sum of its digits in the hundreds, tens and units places is 15, and the tens place digit is 4 more than the units place digit. Then the highest possible 4-digit number satisfying the above conditions is [2021]
Ans: 4195
Sol: Given the 4 digit number:
Considering the number in thousands digit is a number in the hundredth digit is b, number in tens digit is c, number in the units digit is d.
Let the number be abcd.
Given that a + b + c = 14. (1)
b + c + d = 15. (2)
c = d + 4. (3).
In order to find the maximum number which satisfies the condition, we need to have abcd such that a is maximum which is the digit in thousands place in order to maximize the value of the number. b, c, and d are less than 9 each as they are single-digit numbers.
Substituting (3) in (2) we have b + d + 4 + d = 15, b + 2 x d = 11. (4)
Subtracting (2) and (1) : (2) - (1) = d = a+1. (5)
Since c cannot be greater than 9 considering c to be the maximum value 9 the value of d is 5.
If d = 5, using d = a + 1, a = 4.
Hence the maximum value of a = 4 when c = 9, d = 5.
Substituting b + 2 x d = 11. b = 1.
The highest four-digit number satisfying the condition is 4195
Q4: Suppose one of the roots of the equation ax2 - bx + c = 0 is 2+ √3 , Where a,b and c are rational numbers and a ≠ 0. If b = c3 then | a | equals. [2021]
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: Given a, b, c are rational numbers.
Hence a, b, c are three numbers that can be written in the form of p/Q
Hence if one both the root is 2 + √3 and considering the other root to be x.
The sum of the roots and the product of the two roots must be rational numbers.
For this to happen the other root must be the conjugate of 2 + √3 so the product and the sum of the roots are rational numbers which are represented by: b/a, c/a
Hence the sum of the roots is 2 + √3 + 2 - √3 = 4
The product of the roots is 2 + √3 x 2 - √3 =1
b/a = 4, c/a = 1.
b = 4 x a, c= a.
Since b = c3
4 x a = a3
a2 = 4.
a = 2 or -2.
|a| = 2
Q5: For a sequence of real numbers x1 ,x2 ,...xn , If x1 −x2 +x3 −....+(−1)n+1 xn = n2 +2n for all natural numbers n, then the sum x49 + x50 equals [2021]
(a) 200
(b) 2
(c) -200
(d) -2
Ans: (d)
Sol: Now as per the given series :
we get x1 =1 + 2 =3
Now x1 −x2 = 8
So, x2 = -5
Now x1 − x2 + x3 = 15
So, x3 = 7
So, we get
So x49 = 99 and x50 = −101
Therefore x49 + x50 = −2
Q6: For a real number x the condition ∣3x−20∣+∣3x−40∣ = 20 necessarily holds if [2021]
(a) 10 < x < 15
(b) 9 < x < 14
(c) 7 < x < 12
(d) 6 < x < 11
Ans: (c)
Sol: Case 1 : x ≥ 40 / 3
we get 3x - 20 + 3x - 40 = 20
6x = 80
Case 2:
we get 3x - 20 + 40 - 3x = 20
we get 20 = 20
So, we get
Case 3:
we get 20 - 3x + 40 - 3x = 20
40 = 6x
x = 20/3
but this is not possible
so we get from case 1,2 and 3
Now looking at options
we can say only option C satisfies for all x .
Hence 7 < x < 12.
Q7: If n is a positive integer such that 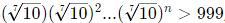 , then the smallest value of n is [2021]
, then the smallest value of n is [2021]
Sol:
For minimum value of n,
1 + 2 + ... + n = 21
We can see that if n = 6, 1 + 2 + 3 + ... + 6 = 21.
Q8: If 3x + 2∣y∣ + y=7 and x + ∣x∣ + 3y = 1 then x + 2yx + 2y is: [2021]
(a) -4/3
(b) 8/3
(c) 0
(d) 1
Ans: (c)
Sol: We need to check for all regions:
x >= 0, y >= 0
x >= 0, y < 0
x < 0, y >= 0
x < 0, y < 0
However, once we find out the answer for any one of the regions, we do not need to calculate for other regions since the options suggest that there will be a single answer.
Let us start with x >= 0, y >= 0,
3x + 3y = 7
2x + 3y = 1
Hence, x = 6 and y = -11/3
Since y > = 0, this is not satisfying the set of rules.
Next, let us test x >= 0, y < 0,
3x - y = 7
2x + 3y = 1
Hence, y = -1
x = 2.
This satisfies both the conditions. Hence, this is the correct point.
We need the value of x + 2y
x + 2y = 2 + 2(-1) = 2 - 2 = 0.
Q9: The number of distinct pairs of integers (m,n), satisfying 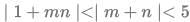 is:
is:
Ans: 12
Sol: Let us break this up into 2 inequations [ Let us assume x as m and y as n ]
| 1 + mn | < | m + n |
| m + n | < 5
Looking at these expressions, we can clearly tell that the graphs will be symmetrical about the origin.
Let us try out with the first quadrant and extend the results to the other quadrants.
We will also consider the +X and +Y axes along with the quadrant.
So, the first inequality becomes,
1 + mn < m + n
1 + mn - m - n < 0
1 - m + mn - n < 0
(1-m) + n(m-1) < 0
(1-m)(1-n) < 0
(m - 1)(n - 1) < 0
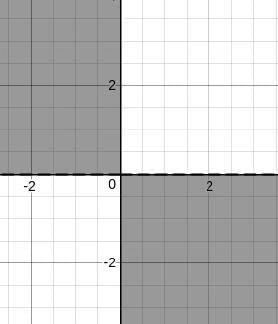
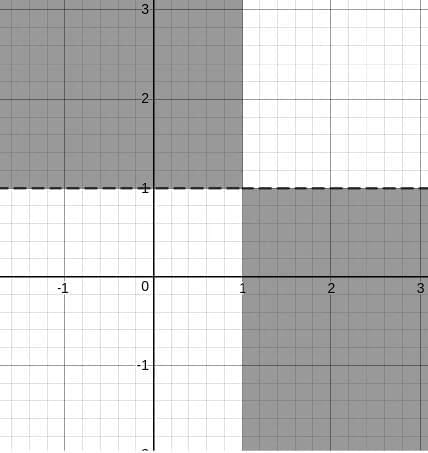
Let us try to plot the graph.
If we consider only mn < 0, then we getBut, we have (m - 1)(n - 1) < 0, so we need to shift the graphs by one unit towards positive x and positive y.
So, we have,But, we are only considering the first quadrant and the +X and +Y axes. Hence, if we extend, we get the following region.
So, if we look for only integer values, we get (0,2), (0,3),.......
(0,-2), (0, -3),......
(2,0), (3,0), ......
(-2,0), (-3,0), .......
Now, let us consider the other inequation as well, in which |x + y| < 5 Since one of the values is always zero, the modulus of the other value is less than or equal to 4.
Hence, we get
(0,2), (0,3), (0,4)
(0,-2), (0, -3), (0, -4)
(2,0), (3,0), (4,0)
(-2,0), (-3,0), (-4,0)
Hence, a total of 12 values.
Q10: A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
Ans: 50
Sol: The question asks for the number of 4 digit numbers using only the digits 1, 2, and 3 such that the digits 2 and 3 appear at least once.
The different possibilities include : Case 1:The four digits are ( 2, 2, 2, 3). Since the number 2 is repeated 3 times.
The total number of arrangements are :Case 2: The four digits are 2, 2, 3, 3. The total number of four-digit numbers formed using this are :
Case 3: The four digits are 2, 3, 3, 3. The number of possible 4 digit numbers are :
Case4: The four digits are 2, 3, 3, 1. The number of possible 4 digit numbers are :
Case5: Using the digits 2, 2, 3, 1. The number of possible 4 digit numbers are :
Case 6: Using the digits 2, 3, 1, 1. The number of possible 4 digit numbers are :
A total of 12 + 12 + 12 + 4 + 6 + 4 = 50 possibilities.
Alternatively
We have to form 4 digit numbers using 1,2,3 such that 2,3 appears at least once
So the possible cases :Now we get
(When one digit is used twice and the remaining two once )
(When 1 is used 0 times and 2 and 3 is used 3 times or 1 time )
(When 2 and 3 is used 2 times each )So total numbers = 36+8+6 =50
2020
Q1: If a, b and c are positive integers such that ab = 432, bc = 96 and c < 9, then the smallest possible value of a + b + c is [2020]
(a) 56
(b) 59
(c) 49
(d) 46
Ans: (d)
Sol: Given ab = 432, bc = 96 and c < 9
To find the minimum value for a + b + c, the two larger numbers should be as close as possible.
The closest combination whose product is 432 is 18 x 24 . For b = 24, we get c = 4 and a = 18 .
Hence the least value for a + b + c = 46 .
Q2: How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7? [2020]
Sol: The product of the digits of the three-digit numbers should be more than 2 and less than 7 .
Hence the possible numbers are as follows.
Q3: The mean of all 4 -digit even natural numbers of the form 'aabb', where a >0, is [2020]
(a) 5050
(b) 4466
(c) 5544
(d) 4864
Ans: (c)
Sol: The sum of possible even digit numbers in the form aabb is 1100 + 1122 + 1144 + 1166 + 1188 + 2200 + 2222 + 2288 + ......9900 + 9922 + 9988 i.e. (45 numbers)
⇒ 1100 + 1100 +1100+ 1100 + 1100 + 22 + 44 + 66 + 88 + 2200 + 2200 + 2200 + 2200 + 2200 +22 + 44 + 66 + 88 +… + 9900 + 9900 + 9900 + 990 + 9900 + 22 + 44 + 66 + 88
⇒ 5(1100 + 2200 + .....9900) + 9(22 + 44 + 66 + 88)5 x 1100(1 + 2 + .... 9) + 9 x 22(1 + 2 + 3 + 4)
⇒ 5500(45) + 45 ´ 44 = 45(5544)
Hence mean =5544
Q4: Let A, B and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is [2020]
(a) 6
(b) 5
(c) 7
(d) 4
Ans: (a)
Sol: Given A, B and C are positive integers such that
The least value for A=1 in which case B=5.
Hence A + B = 6
Q5: If x and y are positive real numbers satisfying x + y=102, then the minimum possible value of 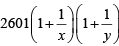 is [2020]
is [2020]
Sol: AM ≥ GM ≥ HM
Given x + y = 102
⇒
⇒
The minimum value of
=
= 2704
Q6: How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3? [2020]
Sol: Consider four blanks
7 is in thousand place, then 3 can be placed in any of the 3 places in 3 ways. Remaining two blanks can be filled with remaining eight digits in 8P2 ways. The number of numbers that have 7 is in thousand place is 3 x 8P2 = 168
Thousand place cannot be 0,7 and 3, it can be filled with remaining 7 digits in 7 ways. In remaining 3 blanks, 7 and 3 can be arranged in 3 ways. Fourth blank can be filled in 7 ways. The number of numbers that are formed where 7 and 3 is not in thousand place is 7 x 3 x 7 = 147 . Hence total required numbers = 168 + 147 = 315.
Q7: In how many ways can a pair of integers (x , a) be chosen such that x2 - 2| x| + | a - 2| = 0? [2020]
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (d)
Sol: x2 - 2| x| + | a- 2 |= 0
If a > 2; | a - 2 |= a - 2
since x is integer 3 - a ≥ 0
a ≤ 3
The possible values of a is = 3
Then x = ± 1;
If a = 2, | x |=| 1 ± 1 |, ⇒ x = ± 2, 0
If a < 2, | a - 2 |= 2 - a
Since x is integer a -1 ≥ 0 ⇒ a ≥ 1
∴ The possible values of a is 1
If a = 1, | x |= 1 ⇒ x = ± 1
∴ The possible pairs =(-1,3), (1,3), (1,1), (-1,1), (2,2),(-2,2), (0,2) i.e., 7
Q8: The number of integers that satisfy the equality ( x2 - 5x + 7 ) x+1 = 1 is [2020]
(a) 2
(b) 3
(c) 5
(d) 4
Ans: (b)
Sol: ( x2 - 5x + 7 ) x+1 = 1
We know, for ab = 1,
if -a = -1 then b is even.
-a = 1 then b is any number
-a > 0 then b = 0
Case 1: x + 1 = 0 Þ x = -1
Case 2: x2 -5x+7 =1 ⇒ x2 -5x + 6 = 0 ⇒ x = 2 or 3
Case 3: x2 -5x + 7 = -1 ⇒ x2 -5x + 8 = 0
but x is not an integer
∴ The number of integers satisfies the equation is 3
Q9: The number of pairs of integers (x , y) satisfying x ≥ y ≥ -20 and 2 x + 5 y = 99 is [2020]
Ans: 2 x + 5 y = 99
When y = - 19, x = 97; since x ≥ y ; the maximum value of y is 13 and corresponding value of x is 17.
We know that the solutions of y are in arithmetic progression with common difference 2.
Here a = - 19, d = 2, tn = 13
tn = a + (n -1)d
-19 + (n - 1)(2) = 13
(n - 1)2 = 32 ⇒ n = 17
Hence number of pairs integers is 17
Q10: If x and y are non-negative integers such that x + 9 = z, y + 1 = z and x + y < z + 5, then the maximum possible value of 2x + y equals [2020]
Sol: Given x + 9 = z = y + 1 and x + y < z + 5
⇒ (z -9) + (z - 1) < z + 5
⇒ z < 15
Hence the maximum value of z = 14, max of x = 5 and max of y = 13
Required answer, 2 x + y = 2 x 5 + 13 = 23
Q11: How many pairs (a, b) of positive integers are there such that a ≤ b and ab = 42017 ? [2020]
(a) 2017
(b) 2019
(c) 2020
(d) 2018
Ans: (b)
Sol: Given, a × b = 42017 = 24034
Since a × b = 42017 , is a perfect square the number of factors of 24034 is odd.
Required answer, the number of values of
= 2018
Q12: If x1 = -1 and xm = xm +1 + (m + 1) for every positive integer $m,$ then x100 equals [2020]
(a) -5151
(b) -5150
(c) -5051
(d) -5050
Ans: (d)
Sol: xm + 1 = xm - (m + 1)
x2 = x1 - 2 = -1 - 2 = -3
x3 = x2 - 3 = -1 - 2 - 3 = - 6
Similarly,
Hence,
= -5050
Q13: Let m and n be natural numbers such that n is even and 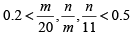 . Then m - 2n equals [2020]
. Then m - 2n equals [2020]
(a) 3
(b) 4
(c) 1
(d) 2
Ans: (c)
Sol: Given,
⇒ n = 4
since 0.2 < n/m < 0.5 m and n = 4, m = 9
m - 2n = 9 - 2 x 4 = 1
Q14: Let N, x and y be positive integers such that N = x + y, 2 < x < 10 and 14 < y < 23. If N > 25, then how many distinct values are possible for N? [2020]
Sol: Given, 2 < x < 10 and 14 < y < 23 Þ 17 < ( x + y ) < 32 i.e. 17 < N < 32
But N > 25 hence 25 < N < 32
N can take 6 distinct values.
Q15: How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7? [2020]
(a) 40
(b) 42
(c) 43
(d) 41
Ans: (d)
Sol: The required answer
=
= 41.14
Required answer is the integral part of 41.14 = 41
|
191 videos|209 docs|103 tests
|
FAQs on Daily Practice Questions CAT Previous Year Questions with Answer PDF
| 1. What are the different types of numbers in the number system? |  |
| 2. How can one determine if a number is irrational? |  |
| 3. What is the significance of prime numbers in the number system? |  |
| 4. How can one simplify complex fractions using the number system concepts? |  |
| 5. How are negative numbers represented in the number system? |  |