Caselets- 1 CAT Previous Year Questions with Answer PDF
2024
Passage
Answer the following questions based on the information given below.
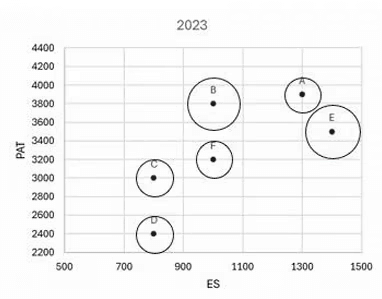
The two plots below give the following information about six firms A, B, C, D, E, and F for 2019 and 2023.
PAT: The firm’s profits after taxes in Rs. crores,
ES: The firm’s employee strength, that is the number of employees in the firm, and
PRD: The percentage of the firm’s PAT that they spend on Research and Development (R&D).
In the plots, the horizontal and vertical coordinates of point representing each firm gives their ES and PAT values respectively. The PRD values of each firm are proportional to the areas around the points representing each firm. The areas are comparable between the two plots, i.e., equal areas in the two plots represent the same PRD values for the two years.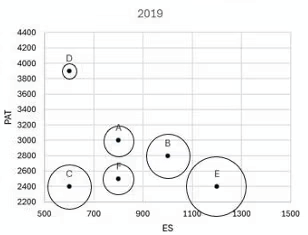
Q1: Assume that the annual rate of growth in PAT over the previous year (ARG) remained constant over the years for each of the six firms. Which among the firms A, B, C, and E had the highest ARG?
(a) Firm A
(b) Firm B
(c) Firm C
(d) Firm E
Ans: (d)
Sol:
Firm A: For Firm A there is a 900Cr increase in PAT from 3000cr to 3900cr
Firm B: For Firm B there is a 1000Cr increase in PAT from 2800cr to 3800cr
Firm C: For Firm C there is a 600Cr increase in PAT from 2400cr to 3000cr
Firm E: For Firm E there is a 1100Cr increase in PAT from 2400 to 3500cr
We can see that Firm E will have the highest ARG as it has grown by 1100Cr from 2400 to 3500Cr.
Q2: The ratio of the amount of money spent by Firm C on R&D in 2019 to that in 2023 is closest to
(a) 5 : 6
(b) 9 : 5
(c) 5 : 9
(d) 9 : 4
Ans: (b)
Sol:
The amount spent by Firm C on R&D in 2019 is > π(2)2x, but < π(3)2x where x is a constant.
The amount spent by Firm C on R&D in 2023 is = π(2)2x, where x is a constant.
So the ratio must be more than 1:1 but less than 9:4
The only possible option is option 2 i.e. 9:5
Q3: Which among the firms A, C, E, and F had the maximum PAT per employee in 2023?
(a) Firm C
(b) Firm E
(c) Firm F
(d) Firm A
Ans: (a)
Sol:
Firm A:
PAT per employee = 3900/1300 = 3Cr
Firm C:
PAT per employee = 30/8 = 3.75Cr
Firm E:
PAT per employee = 3500/1400 = 2.5Cr
Firm F:
PAT per employee = 3200/1000 = 3.2Cr
So the highest will be for Firm C.
Q4: Which among the firms C, D, E, and F had the least amount of R&D spending per employee in 2023?
(a) Firm D
(b) Firm F
(c) Firm E
(d) Firm C
Ans: (a)
Let the proportionality constant be 1/π for PRD
Firm C:
Amount spent = 4% of 3000 crores = 120 crores
Firm D:
Amount spent = 4% of 2400 crores = 96 crores
Firm E:
Amount spent = 6.25% of 3500 crores = 218.75 crores
Firm F:
Amount spent = 4% of 3200crores = 128 crores
So, Firm D had the least amount of R&D spending per employee.
2023
Passage - 1
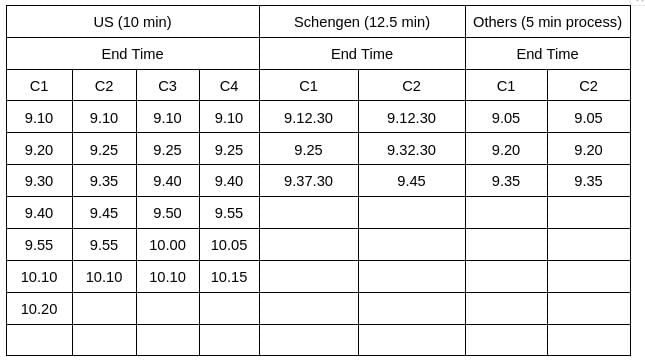
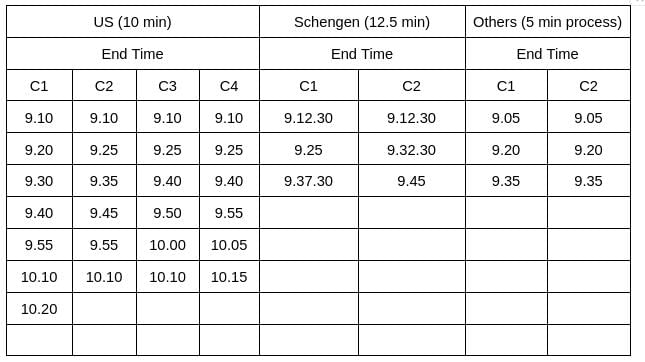
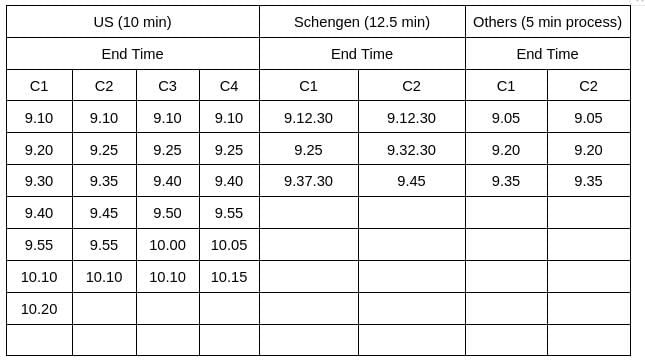
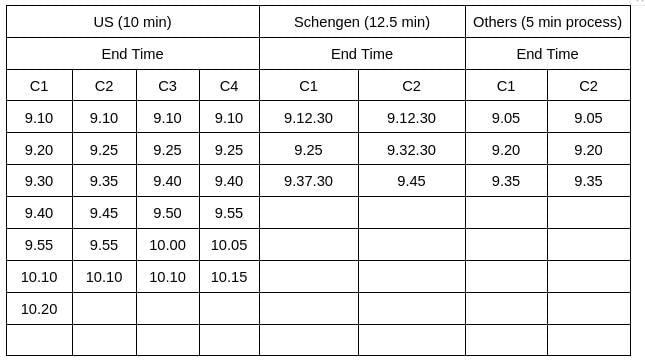
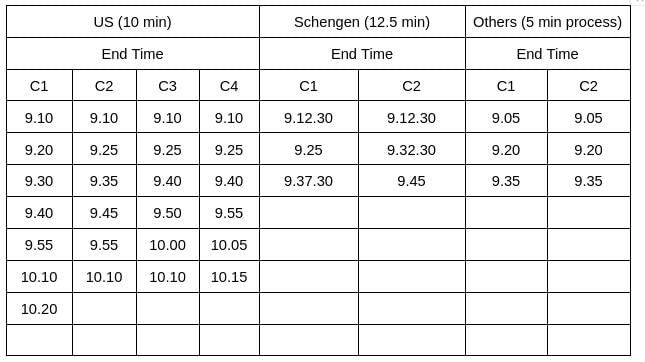
A visa processing office (VPO) accepts visa applications in four categories - US, UK, Schengen, and Others. The applications are scheduled for processing in twenty 15- minute slots starting at 9:00 am and ending at 2:00 pm. Ten applications are scheduled in each slot.
There are ten counters in the office, four dedicated to US applications, and two each for UK applications, Schengen applications and Others applications. Applicants are called in for processing sequentially on a first-come-first-served basis whenever a counter gets freed for their category. The processing time for an application is the same within each category. But it may vary across the categories. Each US and UK application requires 10 minutes of processing time. Depending on the number of applications in a category and time required to process an application for that category, it is possible that an applicant for a slot may be processed later.
On a particular day, Ira, Vijay and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot but entered the VPO at 9:20 am. When they entered the office, exactly six out of the ten counters were either processing applications, or had finished processing one and ready to start processing the next.
Mahira and Osman were scheduled in the 9:30 am slot on that day for visa processing in the Others category.
The following additional information is known about that day.
1. All slots were full.
2. The number of US applications was the same in all the slots. The same was true for the other three categories.
3. 50% of the applications were US applications.
4. All applicants except Ira, Vijay and Nandini arrived on time.
5. Vijay was called to a counter at 9:25 am.
Q1: How many UK applications were scheduled on that day?
Ans: 0
Sol: It is given that the applications are scheduled for processing in twenty 15-minute slots starting at 9:00 am and ending at 2:00 pm. Ten applications are scheduled in each slot.Hence, the total number of applicants = (20*10) = 200. It is also known that 50% of the applications were US applications, and the number of US applications was the same in all the slots. The same was true for the other three categories.
Hence, the number of total number of US applicants = (200*50%) = 100, and the number of US applicants in each slot = (100/20) = 5
It is also known that Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot. Since the number of Schengen applicants was the same in all the slots, it implies the number of Schengen applicants in each slot is at least 3.
Similarly, it is given that Mahira and Osman were scheduled in the 9:30 am slot on that day for visa processing in the Others category, which implies the number of other category applicants in each slot is at least 2. Since the number of total applicants in each slot is 10, this implies the number of Schengen and other applicants in each slot is 3, and 2, respectively. Hence, the number of UK applicants is 0 in each slot.
It is also known that the number of total counters is 10, among which four are dedicated to US applications, and two each for UK applications, Schengen applications, and Others applications. It is given that each US and UK application requires 10 minutes of processing time, and Vijay was called to a counter at 9:25 am. (Who is 5th in the queue). It can only be possible when the processing time of Schengen applications is 12.5 minutes.
On a particular day, Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot but entered the VPO at 9:20 am. When they entered the office, exactly six out of the ten counters were either processing applications, or had finished processing one and ready to start processing the next. Hence, at 9.20 am, there are exactly four free counters. Out of these 4, 2 is the UK counter, and the other two are other counters. (Since the US counters and Schengen Counters were either processing applications, or had finished processing one and were ready to start processing the next.)
From the table, we can say that the total number of UK applicants in each slot is zero, Hence, the total number of applicants is zero.
Q2: What is the maximum possible value of the total time (in minutes, nearest to its integer value) required to process all applications in the Others category on that day?
Ans: 200
Sol: It is given that the applications are scheduled for processing in twenty 15-minute slots starting at 9:00 am and ending at 2:00 pm. Ten applications are scheduled in each slot.Hence, the total number of applicants = (20*10) = 200. It is also known that 50% of the applications were US applications, and the number of US applications was the same in all the slots. The same was true for the other three categories.
Hence, the number of total number of US applicants = (200*50%) = 100, and the number of US applicants in each slot = (100/20) = 5
It is also known that Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot. Since the number of Schengen applicants was the same in all the slots, it implies the number of Schengen applicants in each slot is at least 3.
Similarly, it is given that Mahira and Osman were scheduled in the 9:30 am slot on that day for visa processing in the Others category, which implies the number of other category applicants in each slot is at least 2. Since the number of total applicants in each slot is 10, this implies the number of Schengen and other applicants in each slot is 3, and 2, respectively. Hence, the number of UK applicants is 0 in each slot.
It is also known that the number of total counters is 10, among which four are dedicated to US applications, and two each for UK applications, Schengen applications, and Others applications. It is given that each US and UK application requires 10 minutes of processing time, and Vijay was called to a counter at 9:25 am. (Who is 5th in the queue). It can only be possible when the processing time of Schengen applications is 12.5 minutes.
On a particular day, Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot but entered the VPO at 9:20 am. When they entered the office, exactly six out of the ten counters were either processing applications, or had finished processing one and ready to start processing the next. Hence, at 9.20 am, there are exactly four free counters. Out of these 4, 2 is the UK counter, and the other two are other counters. (Since the US counters and Schengen Counters were either processing applications, or had finished processing one and were ready to start processing the next.)
For the other applicants, the time taken to process one application is at most 5 minutes, which implies the total time taken to process 40 applications is at most (40*5) = 200 minutes.
Q3: Which of the following is the closest to the time when Nandini’s application process got over?
(a) 9:50 am
(b) 9:37 am
(c) 9:35 am
(d) 9:45 am
Ans: (d)
Sol: It is given that the applications are scheduled for processing in twenty 15-minute slots starting at 9:00 am and ending at 2:00 pm. Ten applications are scheduled in each slot.Hence, the total number of applicants = (20*10) = 200. It is also known that 50% of the applications were US applications, and the number of US applications was the same in all the slots. The same was true for the other three categories.
Hence, the number of total number of US applicants = (200*50%) = 100, and the number of US applicants in each slot = (100/20) = 5
It is also known that Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot. Since the number of Schengen applicants was the same in all the slots, it implies the number of Schengen applicants in each slot is at least 3.
Similarly, it is given that Mahira and Osman were scheduled in the 9:30 am slot on that day for visa processing in the Others category, which implies the number of other category applicants in each slot is at least 2. Since the number of total applicants in each slot is 10, this implies the number of Schengen and other applicants in each slot is 3, and 2, respectively. Hence, the number of UK applicants is 0 in each slot.
It is also known that the number of total counters is 10, among which four are dedicated to US applications, and two each for UK applications, Schengen applications, and Others applications. It is given that each US and UK application requires 10 minutes of processing time, and Vijay was called to a counter at 9:25 am. (Who is 5th in the queue). It can only be possible when the processing time of Schengen applications is 12.5 minutes.
On a particular day, Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot but entered the VPO at 9:20 am. When they entered the office, exactly six out of the ten counters were either processing applications, or had finished processing one and ready to start processing the next. Hence, at 9.20 am, there are exactly four free counters. Out of these 4, 2 is the UK counter, and the other two are other counters. (Since the US counters and Schengen Counters were either processing applications, or had finished processing one and were ready to start processing the next.)
Nandini's position was sixth in the queue in the Schengen Applications. From the table, we can see that her process will end at 9.45 am.
The correct option is D
Q4: Which of the following statements is false?
(a) The application process of Osman was completed before 9:45 am.
(b) The application process of Mahira started after Nandini’s.
(c) The application process of Osman was completed before Vijay’s.
(d) The application process of Mahira was completed before Nandini’s.
Ans: (b)
Sol:
It is given that the applications are scheduled for processing in twenty 15-minute slots starting at 9:00 am and ending at 2:00 pm. Ten applications are scheduled in each slot.Hence, the total number of applicants = (20*10) = 200. It is also known that 50% of the applications were US applications, and the number of US applications was the same in all the slots. The same was true for the other three categories.
Hence, the number of total number of US applicants = (200*50%) = 100, and the number of US applicants in each slot = (100/20) = 5
It is also known that Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot. Since the number of Schengen applicants was the same in all the slots, it implies the number of Schengen applicants in each slot is at least 3.
Similarly, it is given that Mahira and Osman were scheduled in the 9:30 am slot on that day for visa processing in the Others category, which implies the number of other category applicants in each slot is at least 2. Since the number of total applicants in each slot is 10, this implies the number of Schengen and other applicants in each slot is 3, and 2, respectively. Hence, the number of UK applicants is 0 in each slot.
It is also known that the number of total counters is 10, among which four are dedicated to US applications, and two each for UK applications, Schengen applications, and Others applications. It is given that each US and UK application requires 10 minutes of processing time, and Vijay was called to a counter at 9:25 am. (Who is 5th in the queue). It can only be possible when the processing time of Schengen applications is 12.5 minutes.
On a particular day, Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot but entered the VPO at 9:20 am. When they entered the office, exactly six out of the ten counters were either processing applications, or had finished processing one and ready to start processing the next. Hence, at 9.20 am, there are exactly four free counters. Out of these 4, 2 is the UK counter, and the other two are other counters. (Since the US counters and Schengen Counters were either processing applications, or had finished processing one and were ready to start processing the next.)
Let's check the options.
Option A: The application process of Osman was completed before 9:45 am. => True (Since he is 5th in the queue, his process will end at 9.35 am)
Option B: The application process of Mahira started after Nandini’s. => The application process for Mahira starts at 9.30 am, and the application process for Nandini starts at 9.32.30 am => False.
The correct option is B
Q5: When did the application processing for all US applicants get over on that day?
(a) 2:05 pm
(b) 2:25 pm
(c) 2:00 pm
(d) 3:40 pm
Ans: (a)
Sol: It is given that the applications are scheduled for processing in twenty 15-minute slots starting at 9:00 am and ending at 2:00 pm. Ten applications are scheduled in each slot.
Hence, the total number of applicants = (20*10) = 200. It is also known that 50% of the applications were US applications, and the number of US applications was the same in all the slots. The same was true for the other three categories.
Hence, the number of total number of US applicants = (200*50%) = 100, and the number of US applicants in each slot = (100/20) = 5
It is also known that Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot. Since the number of Schengen applicants was the same in all the slots, it implies the number of Schengen applicants in each slot is at least 3.
Similarly, it is given that Mahira and Osman were scheduled in the 9:30 am slot on that day for visa processing in the Others category, which implies the number of other category applicants in each slot is at least 2. Since the number of total applicants in each slot is 10, this implies the number of Schengen and other applicants in each slot is 3, and 2, respectively. Hence, the number of UK applicants is 0 in each slot.
It is also known that the number of total counters is 10, among which four are dedicated to US applications, and two each for UK applications, Schengen applications, and Others applications. It is given that each US and UK application requires 10 minutes of processing time, and Vijay was called to a counter at 9:25 am. (Who is 5th in the queue). It can only be possible when the processing time of Schengen applications is 12.5 minutes.
On a particular day, Ira, Vijay, and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot but entered the VPO at 9:20 am. When they entered the office, exactly six out of the ten counters were either processing applications, or had finished processing one and ready to start processing the next. Hence, at 9.20 am, there are exactly four free counters. Out of these 4, 2 is the UK counter, and the other two are other counters. (Since the US counters and Schengen Counters were either processing applications, or had finished processing one and were ready to start processing the next.)
From the table, we can see that the first slot takes 20 minutes to complete, and after that remaining 19 slots take 15 minutes each to complete the US application process.
Hence, the total time taken = 20+15*19 = 305 minutes = 5 hrs 5 minutes. Hence, the time will be (9 am + 5hrs 5 minutes) = 2.05 pm
The correct option is A
Passage - 2
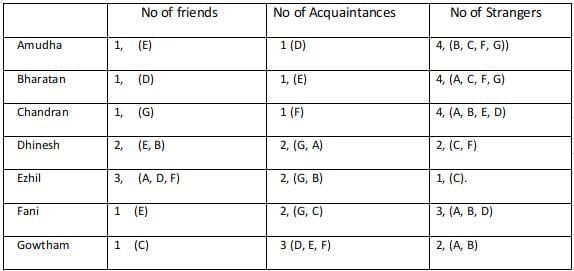
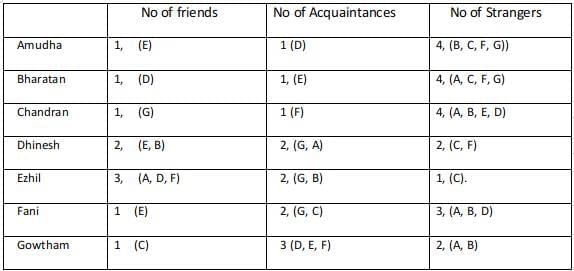
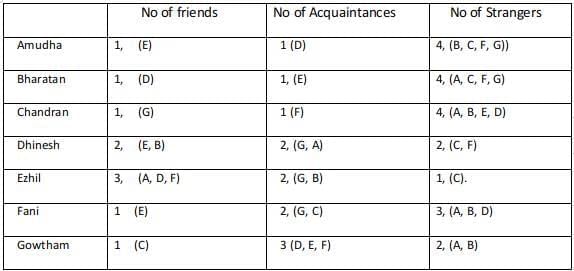
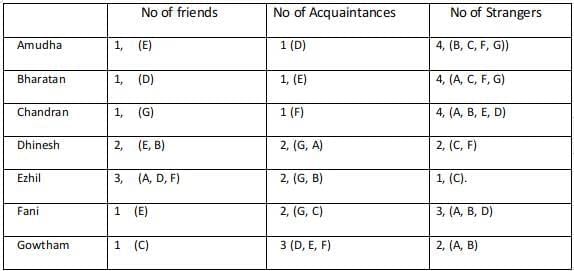
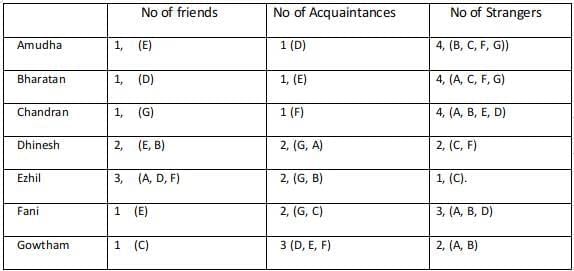
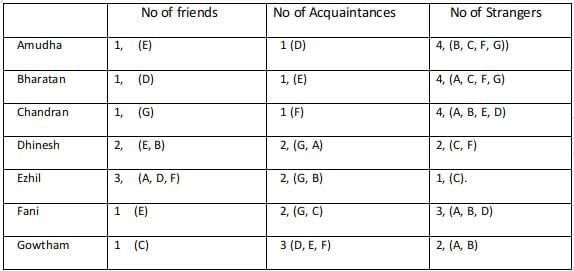
Amudha, Bharatan, Chandran, Dhinesh, Ezhil, Fani and Gowtham are seven people in a town. Any pair of them could either be strangers, acquaintances, or friends. All relationships are mutual. For example, if Amudha is a friend of Bharatan, then Bharatan is also a friend of Amudha. Similarly, if Amudha is a stranger to Bharatan, then Bharatan is also a stranger to Amudha.
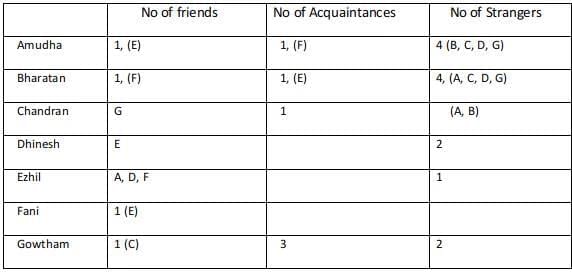
Partial information about the number of friends, acquaintances, and strangers of each of these people among them is given in the table below. The following additional facts are also known.
The following additional facts are also known.
1. Amudha, Bharatan, and Chandran are mutual strangers.
2. Amudha, Dhinesh, and Fani are Ezil's friends.
3. Chandran and Gowtham are friends.
4. Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance of Bharatan is a friend of Amudha.
5. Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan.
Q1: Who are Gowtham’s acquaintances?
(a) Dhinesh, Ezhil and Fani
(b) Amudha, Dhinesh and Fani
(c) Bharatan, Dhinesh and Ezhil
(d) Amudha, Bharatan and Fani
Ans: (a)
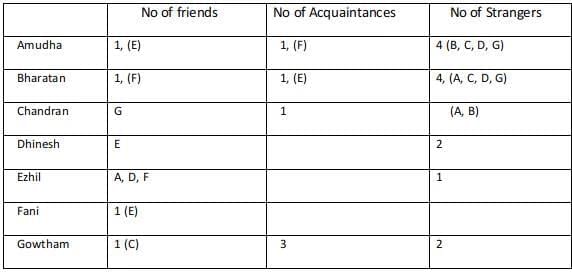
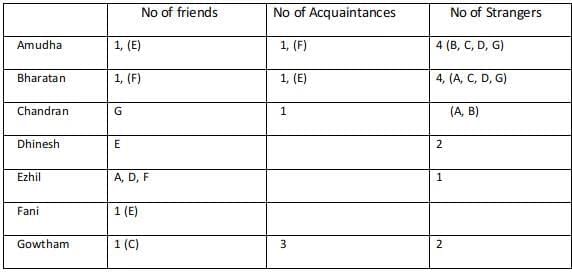
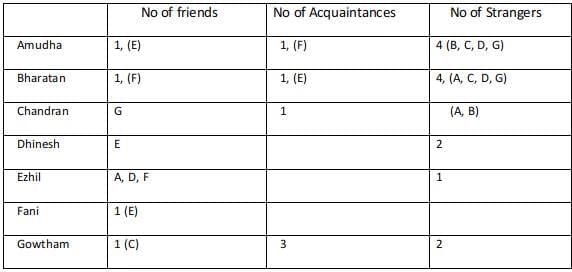
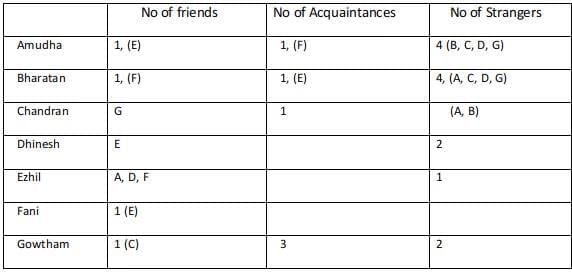
Sol: Since A, B, C are mutual strangers,( B, C )are strangers for A, (A, C) are strangers for B, (A, B) are strangers for C.
Since the total number of strangers+ acquaintances+ friends for any among the 7 is 6.
The number of friends for Amudha is 1, the number of friends for Gowtham is 1.
Using statement 3 Chandran and Gowtham are friends.
Using statement 2: Amudha, Dinesh, and Fani are Ezil’s friends. Similarly, Ezil is a friend of Amudha, Dhinesh, and Fani.
Using statement 4 Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan, Hence the number of acquaintances of Bharatan is equal to the number of friends of Amudha.
Using statement 5 Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance Bharatan is a friend of Amudha, Hence the number of acquaintances of Amudha is equal to the number of friends of Bharatan.
Hence Bharatan has one friend, 1 Acquaintance, 4 strangers.
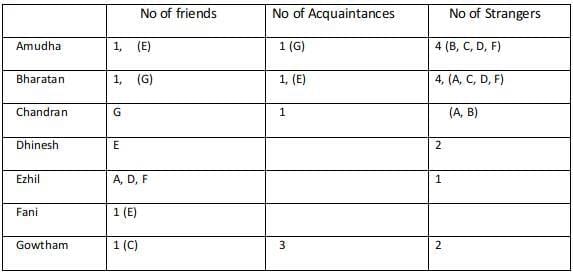
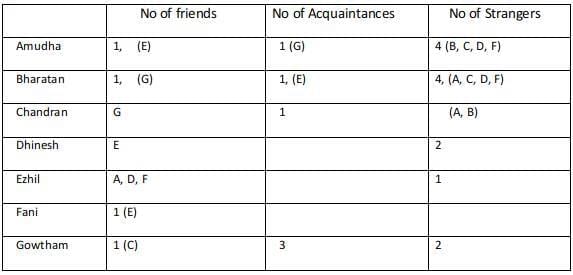
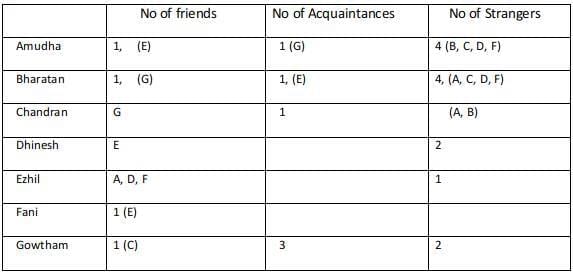
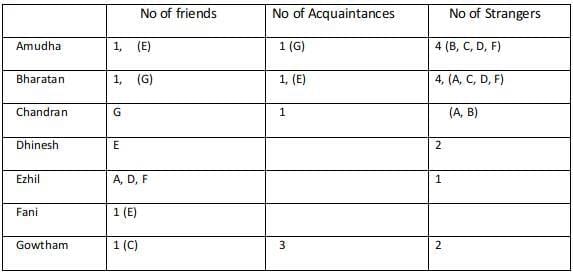
For Amudha we are yet to find a relationship with Dhinesh, Fani, and Gowtham. Any among the three can be the stranger for Amudha, considering the three different cases.Case 1 :
Considering Fani as an acquaintance of Amudha, then Dhinesh and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Fani is an acquaintance of Amudha, hence Amudha is an Acquaintance of Fani, Fani is a friend of Bharathan and hence Bharathan is a friend of Fani. But Fani has only one friend and Ezhil is already a friend of Fani.
Hence this case fails.Case 2:
Considering Gowtham as an acquaintance of Amudha, then Dhinesh and Fani are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.Since Gowtham is a friend of Bharatan, Bharatan must be a friend of Gowtham. But Gowtham can only have one friend and it already mentioned that Chandran is a friend of Gowtham and hence this case fails.
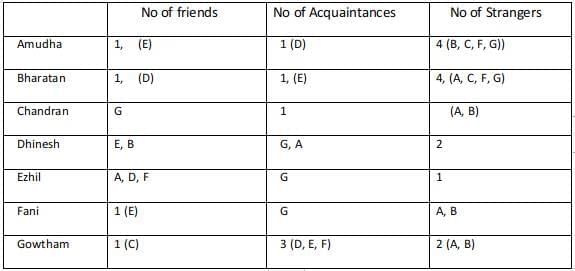
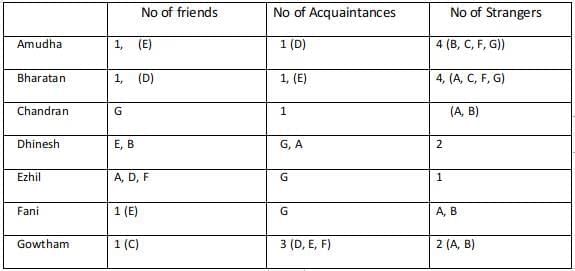
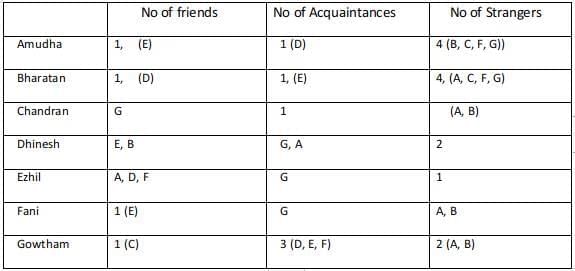
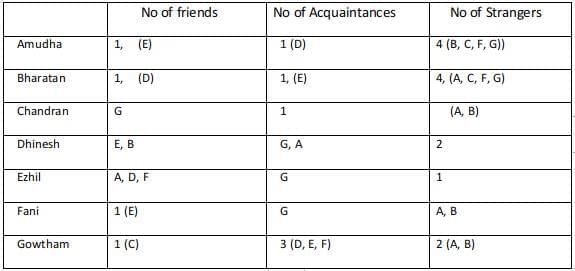
Case 3 :
Considering Dhinesh as an acquaintance of Amudha, then Fani and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Since Fani, Gowtham are strangers to Amudha, Bharatan. Amudha, Bharatan are strangers to Fani, Gowtham.
The 2 strangers to Gowtham and his only friend are known. Hence his three acquaintances are (Dhinesh, Ezhil, Fani).
Hence Gowtham is an acquaintance of Dhinesh, Ezhil, and Fani.
Dhinesh is an acquaintance of Amudha and hence Amudha must be an acquaintance of Dhinesh.
Dhinesh is a friend of Bharatan and hence Bharatan is a friend of Dhinesh.
Ezhil is an acquaintance of Bharatan and hence Bharatan is an acquaintance of Ezhil. The only stranger to Ezhil who is left is Chandran. Hence Ezhil is a stranger to Chandran.
The two strangers to Dhinesh who are left are Chandran and Fani. Chandran is a stranger to Dhinesh and hence Dhinesh is a stranger to Chandran.
The only acquaintance of Chandran who is left is Fani.
The remaining relationships with Fani are Dhinesh and Chandran. Dhinesh is a stranger to Fani and Chandran is an acquaintance of Fani.
Gowtham's Acquaintances are Ghinesh, Ezhil, Fani.
Q2: Who is an acquaintance of Amudha?
(a) Dhinesh
(b) Fani
(c) Gowtham
(d) Ezhil
Ans: (a)
Sol: Since A, B, C are mutual strangers,( B, C )are strangers for A, (A, C) are strangers for B, (A, B) are strangers for C.
Since the total number of strangers+ acquaintances+ friends for any among the 7 is 6.
The number of friends for Amudha is 1, the number of friends for Gowtham is 1.
Using statement 3 Chandran and Gowtham are friends.
Using statement 2: Amudha, Dinesh, and Fani are Ezil’s friends. Similarly, Ezil is a friend of Amudha, Dhinesh, and Fani.
Using statement 4 Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan, Hence the number of acquaintances of Bharatan is equal to the number of friends of Amudha.
Using statement 5 Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance Bharatan is a friend of Amudha, Hence the number of acquaintances of Amudha is equal to the number of friends of Bharatan.
Hence Bharatan has one friend, 1 Acquaintance, 4 strangers.
For Amudha we are yet to find a relationship with Dhinesh, Fani, and Gowtham. Any among the three can be the stranger for Amudha, considering the three different cases.Case 1 :
Considering Fani as an acquaintance of Amudha, then Dhinesh and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Fani is an acquaintance of Amudha, hence Amudha is an Acquaintance of Fani, Fani is a friend of Bharathan and hence Bharathan is a friend of Fani. But Fani has only one friend and Ezhil is already a friend of Fani.
Hence this case fails.Case 2:
Considering Gowtham as an acquaintance of Amudha, then Dhinesh and Fani are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.Since Gowtham is a friend of Bharatan, Bharatan must be a friend of Gowtham. But Gowtham can only have one friend and it already mentioned that Chandran is a friend of Gowtham and hence this case fails.
Case 3 :
Considering Dhinesh as an acquaintance of Amudha, then Fani and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Since Fani, Gowtham are strangers to Amudha, Bharatan. Amudha, Bharatan are strangers to Fani, Gowtham.
The 2 strangers to Gowtham and his only friend are known. Hence his three acquaintances are (Dhinesh, Ezhil, Fani).
Hence Gowtham is an acquaintance of Dhinesh, Ezhil, and Fani.
Dhinesh is an acquaintance of Amudha and hence Amudha must be an acquaintance of Dhinesh.
Dhinesh is a friend of Bharatan and hence Bharatan is a friend of Dhinesh.
Ezhil is an acquaintance of Bharatan and hence Bharatan is an acquaintance of Ezhil. The only stranger to Ezhil who is left is Chandran. Hence Ezhil is a stranger to Chandran.
The two strangers to Dhinesh who are left are Chandran and Fani. Chandran is a stranger to Dhinesh and hence Dhinesh is a stranger to Chandran.
The only acquaintance of Chandran who is left is Fani.
The remaining relationships with Fani are Dhinesh and Chandran. Dhinesh is a stranger to Fani and Chandran is an acquaintance of Fani.Dhinesh is an acquaintance of Amudha
Q3: How many friends does Ezhil have?
Ans: 3
Sol: Since A, B, C are mutual strangers,( B, C )are strangers for A, (A, C) are strangers for B, (A, B) are strangers for C.
Since the total number of strangers+ acquaintances+ friends for any among the 7 is 6.
The number of friends for Amudha is 1, the number of friends for Gowtham is 1.
Using statement 3 Chandran and Gowtham are friends.
Using statement 2: Amudha, Dinesh, and Fani are Ezil’s friends. Similarly, Ezil is a friend of Amudha, Dhinesh, and Fani.
Using statement 4 Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan, Hence the number of acquaintances of Bharatan is equal to the number of friends of Amudha.
Using statement 5 Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance Bharatan is a friend of Amudha, Hence the number of acquaintances of Amudha is equal to the number of friends of Bharatan.
Hence Bharatan has one friend, 1 Acquaintance, 4 strangers.
For Amudha we are yet to find a relationship with Dhinesh, Fani, and Gowtham. Any among the three can be the stranger for Amudha, considering the three different cases.Case 1:
Considering Fani as an acquaintance of Amudha, then Dhinesh and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Fani is an acquaintance of Amudha, hence Amudha is an Acquaintance of Fani, Fani is a friend of Bharathan and hence Bharathan is a friend of Fani. But Fani has only one friend and Ezhil is already a friend of Fani.
Hence this case fails.Case 2:
Considering Gowtham as an acquaintance of Amudha, then Dhinesh and Fani are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.Since Gowtham is a friend of Bharatan, Bharatan must be a friend of Gowtham. But Gowtham can only have one friend and it already mentioned that Chandran is a friend of Gowtham and hence this case fails.
Case 3 :
Considering Dhinesh as an acquaintance of Amudha, then Fani and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Since Fani, Gowtham are strangers to Amudha, Bharatan. Amudha, Bharatan are strangers to Fani, Gowtham.
The 2 strangers to Gowtham and his only friend are known. Hence his three acquaintances are (Dhinesh, Ezhil, Fani).
Hence Gowtham is an acquaintance of Dhinesh, Ezhil, and Fani.
Dhinesh is an acquaintance of Amudha and hence Amudha must be an acquaintance of Dhinesh.
Dhinesh is a friend of Bharatan and hence Bharatan is a friend of Dhinesh.
Ezhil is an acquaintance of Bharatan and hence Bharatan is an acquaintance of Ezhil. The only stranger to Ezhil who is left is Chandran. Hence Ezhil is a stranger to Chandran.
The two strangers to Dhinesh who are left are Chandran and Fani. Chandran is a stranger to Dhinesh and hence Dhinesh is a stranger to Chandran.
The only acquaintance of Chandran who is left is Fani.
The remaining relationships with Fani are Dhinesh and Chandran. Dhinesh is a stranger to Fani and Chandran is an acquaintance of Fani.Ezhil has a total of 3 friends.
Q4: Which of these pairs share the same type of relationship?
(a) (Amudha, Gowtham) and (Ezhil, Fani)
(b) (Bharatan, Chandran) and (Dhinesh, Ezhil)
(c) (Chandran, Ezhil) and (Dhinesh, Gowtham)
(d) (Bharatan, Ezhil) and (Fani, Gowtham)
Ans: (d)
Sol: Since A, B, C are mutual strangers,( B, C )are strangers for A, (A, C) are strangers for B, (A, B) are strangers for C.
Since the total number of strangers+ acquaintances+ friends for any among the 7 is 6.
The number of friends for Amudha is 1, the number of friends for Gowtham is 1.
Using statement 3 Chandran and Gowtham are friends.
Using statement 2: Amudha, Dinesh, and Fani are Ezil’s friends. Similarly, Ezil is a friend of Amudha, Dhinesh, and Fani.
Using statement 4 Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan, Hence the number of acquaintances of Bharatan is equal to the number of friends of Amudha.
Using statement 5 Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance Bharatan is a friend of Amudha, Hence the number of acquaintances of Amudha is equal to the number of friends of Bharatan.
Hence Bharatan has one friend, 1 Acquaintance, 4 strangers.
For Amudha we are yet to find a relationship with Dhinesh, Fani, and Gowtham. Any among the three can be the stranger for Amudha, considering the three different cases.Case 1 :
Considering Fani as an acquaintance of Amudha, then Dhinesh and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Fani is an acquaintance of Amudha, hence Amudha is an Acquaintance of Fani, Fani is a friend of Bharathan and hence Bharathan is a friend of Fani. But Fani has only one friend and Ezhil is already a friend of Fani.
Hence this case fails.Case 2:
Considering Gowtham as an acquaintance of Amudha, then Dhinesh and Fani are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.Since Gowtham is a friend of Bharatan, Bharatan must be a friend of Gowtham. But Gowtham can only have one friend and it already mentioned that Chandran is a friend of Gowtham and hence this case fails.
Case 3 :
Considering Dhinesh as an acquaintance of Amudha, then Fani and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Since Fani, Gowtham are strangers to Amudha, Bharatan. Amudha, Bharatan are strangers to Fani, Gowtham.
The 2 strangers to Gowtham and his only friend are known. Hence his three acquaintances are (Dhinesh, Ezhil, Fani).
Hence Gowtham is an acquaintance of Dhinesh, Ezhil, and Fani.
Dhinesh is an acquaintance of Amudha and hence Amudha must be an acquaintance of Dhinesh.
Dhinesh is a friend of Bharatan and hence Bharatan is a friend of Dhinesh.
Ezhil is an acquaintance of Bharatan and hence Bharatan is an acquaintance of Ezhil. The only stranger to Ezhil who is left is Chandran. Hence Ezhil is a stranger to Chandran.
The two strangers to Dhinesh who are left are Chandran and Fani. Chandran is a stranger to Dhinesh and hence Dhinesh is a stranger to Chandran.
The only acquaintance of Chandran who is left is Fani.
The remaining relationships with Fani are Dhinesh and Chandran. Dhinesh is a stranger to Fani and Chandran is an acquaintance of Fani.In the given options Bharatan and Ezhil are Acauaintances, Fani and Gowtham are acquaintances.
Q5: Who is an acquaintance of Chandran?
(a) Dhinesh
(b) Fani
(c) Ezhil
(d) Bharatan
Ans: (b)
Sol: Since A, B, C are mutual strangers,( B, C )are strangers for A, (A, C) are strangers for B, (A, B) are strangers for C.
Since the total number of strangers+ acquaintances+ friends for any among the 7 is 6.
The number of friends for Amudha is 1, the number of friends for Gowtham is 1.
Using statement 3 Chandran and Gowtham are friends.
Using statement 2: Amudha, Dinesh, and Fani are Ezil’s friends. Similarly, Ezil is a friend of Amudha, Dhinesh, and Fani.
Using statement 4 Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan, Hence the number of acquaintances of Bharatan is equal to the number of friends of Amudha.
Using statement 5 Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance Bharatan is a friend of Amudha, Hence the number of acquaintances of Amudha is equal to the number of friends of Bharatan.
Hence Bharatan has one friend, 1 Acquaintance, 4 strangers.
For Amudha we are yet to find a relationship with Dhinesh, Fani, and Gowtham. Any among the three can be the stranger for Amudha, considering the three different cases.Case 1:
Considering Fani as an acquaintance of Amudha, then Dhinesh and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Fani is an acquaintance of Amudha, hence Amudha is an Acquaintance of Fani, Fani is a friend of Bharathan and hence Bharathan is a friend of Fani. But Fani has only one friend and Ezhil is already a friend of Fani.
Hence this case fails.Case 2:
Considering Gowtham as an acquaintance of Amudha, then Dhinesh and Fani are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.Since Gowtham is a friend of Bharatan, Bharatan must be a friend of Gowtham. But Gowtham can only have one friend and it already mentioned that Chandran is a friend of Gowtham and hence this case fails.
Case 3 :
Considering Dhinesh as an acquaintance of Amudha, then Fani and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Since Fani, Gowtham are strangers to Amudha, Bharatan. Amudha, Bharatan are strangers to Fani, Gowtham.
The 2 strangers to Gowtham and his only friend are known. Hence his three acquaintances are (Dhinesh, Ezhil, Fani).
Hence Gowtham is an acquaintance of Dhinesh, Ezhil, and Fani.
Dhinesh is an acquaintance of Amudha and hence Amudha must be an acquaintance of Dhinesh.
Dhinesh is a friend of Bharatan and hence Bharatan is a friend of Dhinesh.
Ezhil is an acquaintance of Bharatan and hence Bharatan is an acquaintance of Ezhil. The only stranger to Ezhil who is left is Chandran. Hence Ezhil is a stranger to Chandran.
The two strangers to Dhinesh who are left are Chandran and Fani. Chandran is a stranger to Dhinesh and hence Dhinesh is a stranger to Chandran.
The only acquaintance of Chandran who is left is Fani.
The remaining relationships with Fani are Dhinesh and Chandran. Dhinesh is a stranger to Fani and Chandran is an acquaintance of Fani.Fani is an acquaintance of Chandran
Q6: How many people are either a friend or a friend-of-a-friend of Ezhil?
Ans: 4
Sol: Since A, B, C are mutual strangers,( B, C )are strangers for A, (A, C) are strangers for B, (A, B) are strangers for C.
Since the total number of strangers+ acquaintances+ friends for any among the 7 is 6.
The number of friends for Amudha is 1, the number of friends for Gowtham is 1.
Using statement 3 Chandran and Gowtham are friends.
Using statement 2: Amudha, Dinesh, and Fani are Ezil’s friends. Similarly, Ezil is a friend of Amudha, Dhinesh, and Fani.
Using statement 4 Every friend of Bharatan is an acquaintance of Amudha, and every acquaintance of Amudha is a friend of Bharatan, Hence the number of acquaintances of Bharatan is equal to the number of friends of Amudha.
Using statement 5 Every friend of Amudha is an acquaintance of Bharatan, and every acquaintance Bharatan is a friend of Amudha, Hence the number of acquaintances of Amudha is equal to the number of friends of Bharatan.
Hence Bharatan has one friend, 1 Acquaintance, 4 strangers.
For Amudha we are yet to find a relationship with Dhinesh, Fani, and Gowtham. Any among the three can be the stranger for Amudha, considering the three different cases.Case 1 :
Considering Fani as an acquaintance of Amudha, then Dhinesh and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Fani is an acquaintance of Amudha, hence Amudha is an Acquaintance of Fani, Fani is a friend of Bharathan and hence Bharathan is a friend of Fani. But Fani has only one friend and Ezhil is already a friend of Fani.
Hence this case fails.Case 2:
Considering Gowtham as an acquaintance of Amudha, then Dhinesh and Fani are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.Since Gowtham is a friend of Bharatan, Bharatan must be a friend of Gowtham. But Gowtham can only have one friend and it already mentioned that Chandran is a friend of Gowtham and hence this case fails.
Case 3 :
Considering Dhinesh as an acquaintance of Amudha, then Fani and Gowtham are strangers to Amudha.
Every acquaintance of Amudha is a friend of Bharathan and since the friend and acquaintance of Bharatan are known the strangers are found for Bharatan.
Since Fani, Gowtham are strangers to Amudha, Bharatan. Amudha, Bharatan are strangers to Fani, Gowtham.
The 2 strangers to Gowtham and his only friend are known. Hence his three acquaintances are (Dhinesh, Ezhil, Fani).
Hence Gowtham is an acquaintance of Dhinesh, Ezhil, and Fani.
Dhinesh is an acquaintance of Amudha and hence Amudha must be an acquaintance of Dhinesh.
Dhinesh is a friend of Bharatan and hence Bharatan is a friend of Dhinesh.
Ezhil is an acquaintance of Bharatan and hence Bharatan is an acquaintance of Ezhil. The only stranger to Ezhil who is left is Chandran. Hence Ezhil is a stranger to Chandran.
The two strangers to Dhinesh who are left are Chandran and Fani. Chandran is a stranger to Dhinesh and hence Dhinesh is a stranger to Chandran.
The only acquaintance of Chandran who is left is Fani.
The remaining relationships with Fani are Dhinesh and Chandran. Dhinesh is a stranger to Fani and Chandran is an acquaintance of Fani.Ezhil has Amudha, Dhinesh, Fani as his friends. Dinesh has Bharatan as his friend. Hence a total of 4 (Amudha, Bharatan, Dhinesh, and Fani) are his friends or friend of a friend.
Passage - 3
Each of the bottles mentioned in this question contains 50 ml of liquid. The liquid in any bottle can be 100% pure content (P) or can have certain amount of impurity (I). Visually it is not possible to distinguish between P and I. There is a testing device which detects impurity, as long as the percentage of impurity in the content tested is 10% or more.
For example, suppose bottle 1 contains only P, and bottle 2 contains 80% P and 20% I. If content from bottle 1 is tested, it will be found out that it contains only P. If content of bottle 2 is tested, the test will reveal that it contains some amount of I. If 10 ml of content from bottle 1 is mixed with 20 ml content from bottle 2, the test will show that the mixture has impurity, and hence we can conclude that at least one of the two bottles has I. However, if 10 ml of content from bottle 1 is mixed with 5 ml of content from bottle 2. the test will not detect any impurity in the resultant mixture.
Q1: 5 ml of content from bottle A is mixed with 5 ml of content from bottle B. The resultant mixture, when tested, detects the presence of I. If it is known that bottle A contains only P, what BEST can be concluded about the volume of I in bottle B?
(a) 1 ml
(b) Less than 1 ml
(c) 10 ml
(d) 10 ml or more
Ans: (d)
Sol: Given that each of the bottles contains a volume of 50 ml each.
If 5 ml from bottle A which contains only P is mixed with 5 ml of bottle B and in the resultant mixture the presence of I was detected.
In order to detect the presence of I in this, there must be at least 10% impurity in the 10 ml which is equivalent to 1 ml. This must be from bottle B.
Hence 5 ml of solution from B must contain at least 1ml of impurity and since bottle B is of a total volume of 50 ml. This must contain at least 10 ml of impurity.
Q2: There are four bottles. It is known that three of these bottles contain only P, while the remaining one contains 80% P and 20% I. What is the minimum number of tests required to definitely identify the bottle containing some amount of I?
Ans: 2
Sol: The percentage concentration of the impure solution is 80 percent.
When equal volumes of all four solutions are mixed.
Considering 10 ml of each we have impurity to be 2ml/40ml. The impurity concentration is less than 10 percent and hence cannot be recognized.
Similarly when equal volumes of one impure and 2 pure solutions are mixed.
The impurity in the solution is 2ml/30ml which is less than 10 percent and hence cannot be recognized.
Hence for detecting the impure solution we must use equal volumes of 2 solutions at a time.
Considering the three pure solutions to be P and the impure solution to be I.
P, P, P, I.
Considering equal volumes of solution from the bottle one bottle of P, and I. Testing this would recognize the impurity.
After this consider one bottle among the other 2 P bottles which are left and test this with one among the previously tested P, I.
If the one considered is I it will detect the impurity and confirms the bottle to be I.
If the one considered is P it will fail to detect the impurity and hence the other bottle will be I.
Hence a minimum of two tests are required to identify the bottle with the impurity.
Q3: There are four bottles. Each bottle is known to contain only P or only I. They will be considered to be “collectively ready for despatch” if all of them contain only P. In minimum how many tests, is it possible to ascertain whether these four bottles are “collectively ready for despatch”?
Ans: 1
Sol: The bottles contain either P(pure) or I(impure). The possible cases here are :
1- (P, P, P, P), 2-(P,P,P,I), 3-(P,P,I,I), 4-(P,I,I,I), 5-(I,I,I,I).
In the first case if all the four solutions are pure then taking equal volumes of all the four bottles will get the result to dispatch or not to dispatch.
In the second case if 3 bottles are pure and one impure taking equal volumes of all four bottles and testings will confirm the impurity and hence cannot be dispatched.
In the third case if 2 bottles are pure and two are impure taking equal volumes of all four bottles and testing will confirm the impurity and hence cannot be dispatched.
In the fourth case when only one bottle is pure taking equal volumes of all four bottles will confirm the impurity and hence cannot be dispatched.
In the fifth case if all four bottles are impure taking equal volumes of the four bottles will confirm the impurity and hence cannot be dispatched.
In all the cases a single test is enough to determine if the lot is to be dispatched or not.
Q4: There are four bottles. It is known that either one or two of these bottles contain(s) only P, while the remaining ones contain 85% P and 15% I. What is the minimum number of tests required to ascertain the exact number of bottles containing only P?
(a) 4
(b) 2
(c) 3
(d) 1
Ans: (d)
Sol: The bottles could possibly be :
Case - 1 Pure, Impure, Impure, Impure.
Case-2, Pure , Pure, Impure, Impure.
Since the concentration in the impure bottle is 85 percent.
In case 1 when equal volumes from all the bottles are considered and mixed. The test result detects the impurity..
Since the overall concentration of impurity is greater than 10 percent.
Considering 10 ml from all four bottles.
The impure concentration is 4.5ml/40ml which is greater than 10.(15ml*3 = 4.5ml) (Impurity is detected)
For case 2 when all four bottles are considered. The case here has 2 pure and 2 impure bottles.
When equal volumes from all four bottles are mixed. The resultant concentration of impurity when 10 ml from each of the four solutions is considered :
The impure concentration is 3ml/40ml which is less than 10 percent.. (1.5ml*2 = 3ml). (Impurity is not detected.)
Hence in one possibility the impurity is detected and not detected in the other case. A single test is enough based on the results of which the number of pure and the number of impure bottles can be identified.
Passage - 4
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
1. Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
2. Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
3. Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
4. Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
Q1: How many questions were DEFINITELY created by Amal?
Ans: 3
Sol: For a question created by externals(SME), the minimum number of reviews required is two and the maximum number of reviews is three to confirm the acceptance or the rejection.
For a question created by anyone among Amal, Bimal, Komal a question can be reviewed after one review or two reviews.
The information provided states :
Q02, Q06, Q09, Q11, and Q12 were rejected. Q01, Q03, Q04, Q05, Q07, Q08, Q10, Q13 were accepted.
For the questions :
Amal - Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
Bimal - Q02, Q04, Q06, Q07, Q08, Q09, Q12, and Q13.
Komal - Q01, Q02, Q03, Q04, Q05, Q07, Q08, Q09, Q11, and Q12.Q01 is reviewed by only Komal and is accepted hence Bimal must have prepared the question as it was accepted in a single review. (Bimal)
Q02-is reviewed by Amal, Bimal, and Komal and was rejected this has a possibility of being prepared by an external person and faced rejection by one among Amal and Bimal and Komal. (SME).
Q03-Was accepted and reviewed by Amal, Komal and hence must have been prepared by Bimal(Bimal).
Q04- Accepted and reviewed by the three of them and hence must have been prepared by an external expert. (SME).
Q05-Only reviewed by Komal and is accepted and hence must be prepared by Bimal. (Bimal)
Q06-Rejected and reviewed by Amal and Bimal. Hence could have been prepared by Komal or External and rejected by Bimal and Amal. (Komal/SME).
Q07-Accepted and reviewed by Bimal and Komal. Hence must have been prepared by Amal. (Amal).
Q08- Reviewed by Amal, Bimal, and Komal and is accepted. Hence must have been prepared by SME. (SME)
Q09- Reviewed by Bimal and Komal and is rejected. It must have been prepared by Amal and was rejected by both of them. (Amal).
Q10- Was reviewed by Amal and was accepted. Must have been prepared by Komal. (Komal)
Q11- Reviewed by Amal and Komal and was rejected. Must have been prepared by Bimal and rejected by both Amal and Komal. (Bimal)
Q12- Reviewed by Bimal and Komal and was rejected. Must have been prepared by Amal and was rejected by both Bimal and Komal. (Amal).
Q13- Reviewed by Amal and Bimal and was accepted. The question could have been prepared by Komal or SME. (Komal/SME).
Amal definitely prepared questions Q07, Q09, Q12.
Q2: How many questions were DEFINITELY created by the SMEs?
Ans: 3
Sol: For a question created by externals(SME), the minimum number of reviews required is two and the maximum number of reviews is three to confirm the acceptance or the rejection.
For a question created by anyone among Amal, Bimal, Komal a question can be reviewed after one review or two reviews.The information provided states :
Q02, Q06, Q09, Q11, and Q12 were rejected. Q01, Q03, Q04, Q05, Q07, Q08, Q10, Q13 were accepted.For the questions :
Amal - Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
Bimal - Q02, Q04, Q06, Q07, Q08, Q09, Q12, and Q13.
Komal - Q01, Q02, Q03, Q04, Q05, Q07, Q08, Q09, Q11, and Q12.Q01 is reviewed by only Komal and is accepted hence Bimal must have prepared the question as it was accepted in a single review. (Bimal)
Q02-is reviewed by Amal, Bimal, and Komal and was rejected this has a possibility of being prepared by an external person and faced rejection by one among Amal and Bimal and Komal. (SME).
Q03-Was accepted and reviewed by Amal, Komal and hence must have been prepared by Bimal(Bimal).
Q04- Accepted and reviewed by the three of them and hence must have been prepared by an external expert. (SME).
Q05-Only reviewed by Komal and is accepted and hence must be prepared by Bimal. (Bimal)
Q06-Rejected and reviewed by Amal and Bimal. Hence could have been prepared by Komal or External and rejected by Bimal and Amal. (Komal/SME).
Q07-Accepted and reviewed by Bimal and Komal. Hence must have been prepared by Amal. (Amal).
Q08- Reviewed by Amal, Bimal, and Komal and is accepted. Hence must have been prepared by SME. (SME)
Q09- Reviewed by Bimal and Komal and is rejected. It must have been prepared by Amal and was rejected by both of them. (Amal).
Q10- Was reviewed by Amal and was accepted. Must have been prepared by Komal. (Komal)
Q11- Reviewed by Amal and Komal and was rejected. Must have been prepared by Bimal and rejected by both Amal and Komal. (Bimal)
Q12- Reviewed by Bimal and Komal and was rejected. Must have been prepared by Amal and was rejected by both Bimal and Komal. (Amal).
Q13- Reviewed by Amal and Bimal and was accepted. The question could have been prepared by Komal or SME. (Komal/SME).
Q02, Q04, Q08 were prepared SME
Q3: The approval ratio of a reviewer is the ratio of the number of questions (s)he approved to the number of questions (s)he reviewed. Which option best describes Amal’s approval ratio?
(a) either 0.25 or 0.75
(b) 0.25
(c) lies between 0.25 and 0.50
(d) lies between 0.25 and 0.75
Ans: (d)
Sol: For a question created by externals(SME), the minimum number of reviews required is two and the maximum number of reviews is three to confirm the acceptance or the rejection.
For a question created by anyone among Amal, Bimal, Komal a question can be reviewed after one review or two reviews.
The information provided states :
Q02, Q06, Q09, Q11, and Q12 were rejected. Q01, Q03, Q04, Q05, Q07, Q08, Q10, Q13 were accepted.For the questions :
Amal - Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
Bimal - Q02, Q04, Q06, Q07, Q08, Q09, Q12, and Q13.
Komal - Q01, Q02, Q03, Q04, Q05, Q07, Q08, Q09, Q11, and Q12.Q01 is reviewed by only Komal and is accepted hence Bimal must have prepared the question as it was accepted in a single review. (Bimal)
Q02-is reviewed by Amal, Bimal, and Komal and was rejected this has a possibility of being prepared by an external person and faced rejection by one among Amal and Bimal and Komal. (SME).
Q03-Was accepted and reviewed by Amal, Komal and hence must have been prepared by Bimal(Bimal).
Q04- Accepted and reviewed by the three of them and hence must have been prepared by an external expert. (SME).
Q05-Only reviewed by Komal and is accepted and hence must be prepared by Bimal. (Bimal)
Q06-Rejected and reviewed by Amal and Bimal. Hence could have been prepared by Komal or External and rejected by Bimal and Amal. (Komal/SME).
Q07-Accepted and reviewed by Bimal and Komal. Hence must have been prepared by Amal. (Amal).
Q08- Reviewed by Amal, Bimal, and Komal and is accepted. Hence must have been prepared by SME. (SME)
Q09- Reviewed by Bimal and Komal and is rejected. It must have been prepared by Amal and was rejected by both of them. (Amal).
Q10- Was reviewed by Amal and was accepted. Must have been prepared by Komal. (Komal)
Q11- Reviewed by Amal and Komal and was rejected. Must have been prepared by Bimal and rejected by both Amal and Komal. (Bimal)
Q12- Reviewed by Bimal and Komal and was rejected. Must have been prepared by Amal and was rejected by both Bimal and Komal. (Amal).
Q13- Reviewed by Amal and Bimal and was accepted. The question could have been prepared by Komal or SME. (Komal/SME).Amal reviewed the questions :
Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
For Q2 - Amal can either approve or reject the question.
For Q3- Amal must approve the question.
For Q4 -Amal can either approve or reject the question.
For Q06 - Amal must reject the question.
For Q08 - Amal can either approve or reject the question.
For Q10 - Amal must approve the question.
For Q11 - Amal must reject the question.
For Q13- Amal can either approve or reject the question.
The approval ratio has a minimum of 2 questions only Q3, Q10, and a maximum of 6 questions Q02, Q3, Q04, Q08, Q10, Q13.
Hence 2/8 = 0.25 to 6/8 = 0.75
Q4: How many questions were DEFINITELY created by Komal?
Ans: 1
Sol: For a question created by externals(SME), the minimum number of reviews required is two and the maximum number of reviews is three to confirm the acceptance or the rejection.
For a question created by anyone among Amal, Bimal, Komal a question can be reviewed after one review or two reviews.The information provided states :
Q02, Q06, Q09, Q11, and Q12 were rejected. Q01, Q03, Q04, Q05, Q07, Q08, Q10, Q13 were accepted.For the questions :
Amal - Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
Bimal - Q02, Q04, Q06, Q07, Q08, Q09, Q12, and Q13.
Komal - Q01, Q02, Q03, Q04, Q05, Q07, Q08, Q09, Q11, and Q12.Q01 is reviewed by only Komal and is accepted hence Bimal must have prepared the question as it was accepted in a single review. (Bimal)
Q02-is reviewed by Amal, Bimal, and Komal and was rejected this has a possibility of being prepared by an external person and faced rejection by one among Amal and Bimal and Komal. (SME).
Q03-Was accepted and reviewed by Amal, Komal and hence must have been prepared by Bimal(Bimal).
Q04- Accepted and reviewed by the three of them and hence must have been prepared by an external expert. (SME).
Q05-Only reviewed by Komal and is accepted and hence must be prepared by Bimal. (Bimal)
Q06-Rejected and reviewed by Amal and Bimal. Hence could have been prepared by Komal or External and rejected by Bimal and Amal. (Komal/SME).
Q07-Accepted and reviewed by Bimal and Komal. Hence must have been prepared by Amal. (Amal).
Q08- Reviewed by Amal, Bimal, and Komal and is accepted. Hence must have been prepared by SME. (SME)
Q09- Reviewed by Bimal and Komal and is rejected. It must have been prepared by Amal and was rejected by both of them. (Amal).
Q10- Was reviewed by Amal and was accepted. Must have been prepared by Komal. (Komal)
Q11- Reviewed by Amal and Komal and was rejected. Must have been prepared by Bimal and rejected by both Amal and Komal. (Bimal)
Q12- Reviewed by Bimal and Komal and was rejected. Must have been prepared by Amal and was rejected by both Bimal and Komal. (Amal).
Q13- Reviewed by Amal and Bimal and was accepted. The question could have been prepared by Komal or SME. (Komal/SME).
Q10 was definitely prepared by Komal.
Q5: How many questions were DEFINITELY disapproved by Bimal?
(a) 3
(b) 4
(c) 7
(d) 5
Ans: (b)
Sol: For a question created by externals(SME), the minimum number of reviews required is two and the maximum number of reviews is three to confirm the acceptance or the rejection.
For a question created by anyone among Amal, Bimal, Komal a question can be reviewed after one review or two reviews.
The information provided states :
Q02, Q06, Q09, Q11, and Q12 were rejected. Q01, Q03, Q04, Q05, Q07, Q08, Q10, Q13 were accepted.For the questions :
Amal - Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
Bimal - Q02, Q04, Q06, Q07, Q08, Q09, Q12, and Q13.
Komal - Q01, Q02, Q03, Q04, Q05, Q07, Q08, Q09, Q11, and Q12.Q01 is reviewed by only Komal and is accepted hence Bimal must have prepared the question as it was accepted in a single review. (Bimal)
Q02-is reviewed by Amal, Bimal, and Komal and was rejected this has a possibility of being prepared by an external person and faced rejection by one among Amal and Bimal and Komal. (SME).
Q03-Was accepted and reviewed by Amal, Komal and hence must have been prepared by Bimal(Bimal).
Q04- Accepted and reviewed by the three of them and hence must have been prepared by an external expert. (SME).
Q05-Only reviewed by Komal and is accepted and hence must be prepared by Bimal. (Bimal)
Q06-Rejected and reviewed by Amal and Bimal. Hence could have been prepared by Komal or External and rejected by Bimal and Amal. (Komal/SME).
Q07-Accepted and reviewed by Bimal and Komal. Hence must have been prepared by Amal. (Amal).
Q08- Reviewed by Amal, Bimal, and Komal and is accepted. Hence must have been prepared by SME. (SME)
Q09- Reviewed by Bimal and Komal and is rejected. It must have been prepared by Amal and was rejected by both of them. (Amal).
Q10- Was reviewed by Amal and was accepted. Must have been prepared by Komal. (Komal)
Q11- Reviewed by Amal and Komal and was rejected. Must have been prepared by Bimal and rejected by both Amal and Komal. (Bimal)
Q12- Reviewed by Bimal and Komal and was rejected. Must have been prepared by Amal and was rejected by both Bimal and Komal. (Amal).
Q13- Reviewed by Amal and Bimal and was accepted. The question could have been prepared by Komal or SME. (Komal/SME).
Q06 irrespective of the question prepared by Komal/SME Bimal must reject the question.
Q07, Q09, Q12 are prepared by Amal and were reviewed by Bimal first and Komal next for this to happen Bimal must reject these questions.
Hence a total of four questions were rejected by Bimal.
Q6: How many questions created by Amal or Bimal were disapproved by at least one of the other reviewers?
(a) 7
(b) 4
(c) 5
(d) 2
Ans: (c)
Sol: For a question created by externals(SME), the minimum number of reviews required is two and the maximum number of reviews is three to confirm the acceptance or the rejection.
For a question created by anyone among Amal, Bimal, Komal a question can be reviewed after one review or two reviews.
The information provided states :
Q02, Q06, Q09, Q11, and Q12 were rejected. Q01, Q03, Q04, Q05, Q07, Q08, Q10, Q13 were accepted.For the questions :
Amal - Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
Bimal - Q02, Q04, Q06, Q07, Q08, Q09, Q12, and Q13.
Komal - Q01, Q02, Q03, Q04, Q05, Q07, Q08, Q09, Q11, and Q12.Q01 is reviewed by only Komal and is accepted hence Bimal must have prepared the question as it was accepted in a single review. (Bimal)
Q02-is reviewed by Amal, Bimal, and Komal and was rejected this has a possibility of being prepared by an external person and faced rejection by one among Amal and Bimal and Komal. (SME).
Q03-Was accepted and reviewed by Amal, Komal and hence must have been prepared by Bimal(Bimal).
Q04- Accepted and reviewed by the three of them and hence must have been prepared by an external expert. (SME).
Q05-Only reviewed by Komal and is accepted and hence must be prepared by Bimal. (Bimal)
Q06-Rejected and reviewed by Amal and Bimal. Hence could have been prepared by Komal or External and rejected by Bimal and Amal. (Komal/SME).
Q07-Accepted and reviewed by Bimal and Komal. Hence must have been prepared by Amal. (Amal).
Q08- Reviewed by Amal, Bimal, and Komal and is accepted. Hence must have been prepared by SME. (SME)
Q09- Reviewed by Bimal and Komal and is rejected. It must have been prepared by Amal and was rejected by both of them. (Amal).
Q10- Was reviewed by Amal and was accepted. Must have been prepared by Komal. (Komal)
Q11- Reviewed by Amal and Komal and was rejected. Must have been prepared by Bimal and rejected by both Amal and Komal. (Bimal)
Q12- Reviewed by Bimal and Komal and was rejected. Must have been prepared by Amal and was rejected by both Bimal and Komal. (Amal).
Q13- Reviewed by Amal and Bimal and was accepted. The question could have been prepared by Komal or SME. (Komal/SME).Amal could have possibly created the questions :
Q07, Q09, Q12 of which all three of them were reviewed by two people each, and hence they must have been rejected by the first reviewer.Bimal could have created the questions :
Q01, Q03, Q05, Q 11.
Q01, Q05 are reviewed only by Komal and hence did not have any rejection.
Q03, Q11 faced at least one rejection.
Hence a total of five questions.
|
77 videos|180 docs|96 tests
|
FAQs on Caselets- 1 CAT Previous Year Questions with Answer PDF
| 1. What is the significance of data caselets in the CAT exam? |  |
| 2. How many data caselets can be expected in the CAT exam? |  |
| 3. What skills are required to effectively solve data caselets in the CAT exam? |  |
| 4. How can I improve my performance in solving data caselets for the CAT exam? |  |
| 5. Are there any specific strategies or tips for solving data caselets in the CAT exam? |  |