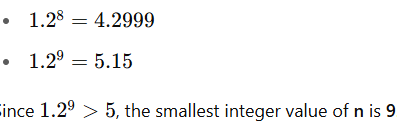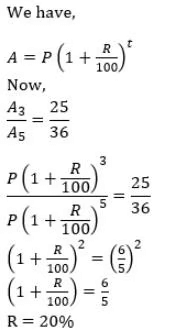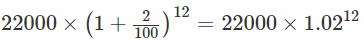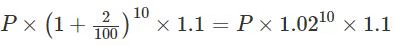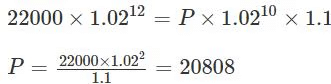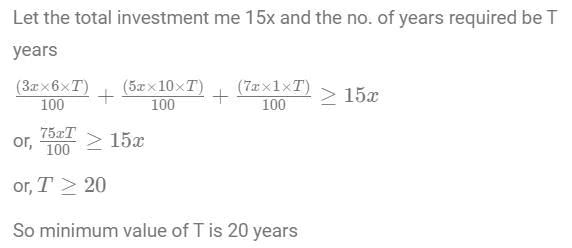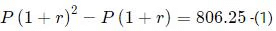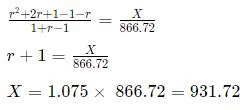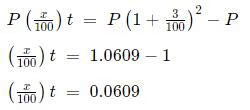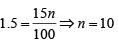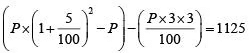Simple & Compound Interest CAT Previous Year Questions with Answer PDF
2024
Q1: An amount of Rs 10000 is deposited in bank A for a certain number of years at a simple interest of 5% per annum. On maturity, the total amount received is deposited in bank B for another 5 years at a simple interest of 6% per annum. If the interests received from bank A and bank B are in the ratio 10 : 13, then the investment period, in years, in bank A is [2024]
(a) 6
(b) 5
(c) 3
(d) 4
Ans: (a)
Sol: We are told that, 10000 is deposited in bank A for a certain number of years at a simple interest of 5% per annum.
Let us say that the number of years is x
Total value of the deposit after x years is, 10000 ( 1 + x ( 0.05 ))
On maturity, the total amount received is deposited in bank B for another 5 years at a simple interest of 6% per annum
Here we know the years and the interest rate,
10000(1 + x(0.05))(1 + 5(0.06))
10000(1+(0.05)x)(1.3)
Interest received from Bank A= (x(0.05))10000
Interest received from Bank B = 0.3(10000(1+x(0.05)))
This ratio is given to be 10:13.Hence the number of years the money was invested in Bank A is 6 years.
Q2: Anil invests Rs 22000 for 6 years in a scheme with 4% interest per annum, compounded half-yearly. Separately, Sunil invests a certain amount in the same scheme for 5 years, and then reinvests the entire amount he receives at the end of 5 years, for one year at 10% simple interest. If the amounts received by both at the end of 6 years are equal, then the initial investment, in rupees, made by Sunil is [2024]
(a) 20808
(b) 20860
(c) 20480
(d) 20640
Ans: (a)
Sol:1. Calculate Anil’s amount after 6 years with 4% p.a. compounded half-yearly:
Anil’s formula:
Aₐ = 22000 × (1 + 0.04/2)¹² = 22000 × (1.02)¹² ≈ 22000 × 1.26824 ≈ 27861.312. Calculate Sunil’s amount after 5 years (compounded half-yearly) and 1 year of simple interest:
After 5 years:
Aₛ = P × (1 + 0.04/2)¹⁰ = P × (1.02)¹⁰Reinvested for 1 year at 10% simple interest:
Aₛ = P × (1.02)¹⁰ × 1.103. Set the amounts equal and solve for P:
22000 × (1.02)¹² = P × (1.02)¹⁰ × 1.10
Simplify:
P = (22000 × (1.02)²) / 1.10 = (22000 × 1.0404) / 1.10 = 22888.8 / 1.10 = 20808
Q3: Aman invests Rs 4000 in a bank at a certain rate of interest, compounded annually. If the ratio of the value of the investment after 3 years to the value of the investment after 5 years is 25 : 36, then the minimum number of years required for the value of the investment to exceed Rs 20000 is [2024]
Ans: 9
Sol:Let us assume the amount invested to be P, and the rate of interest to be r.
Value of the investment after 3 years = P × (1 + r)³
Value of the investment after 5 years = P × (1 + r)⁵
Now given:
Now we need to find the value of n such that:
4000 × (1 + r)ⁿ > 20000
Which becomes:
(1.2)ⁿ > 5Now testing powers of 1.2:
Q4: Anil invests Rs 22000 for 6 years in a scheme with 4% interest per annum, compounded half-yearly. Separately, Sunil invests a certain amount in the same scheme for 5 years, and then reinvests the entire amount he receives at the end of 5 years, for one year at 10% simple interest. If the amounts received by both at the end of 6 years are equal, then the initial investment, in rupees, made by Sunil is
(a) 20808
(b) 20860
(c) 20480
(d) 20640
Ans: (a)
Sol: Assume the amount invested by Sunil be A.
The amount received by Anil at the end of 6 yearsThe amount received by Sunil at the end of 5 years = A × (1.02)10
After the end of 5 years, Sunil invests this amount at a 10% of simple interest.
So, the total amount with Sunil at the end of 6 years = A × (1.02)10 × (1 + 0.1)
In the question, it is given that, the final amount with Sunil and Anil is equal.
So, A(1.02)10 × (1.1) = 22000(1.02)12
A = 20808
Hence, A is the required answer.
Q5: Aman invests Rs 4000 in a bank at a certain rate of interest, compounded annually. If the ratio of the value of the investment after 3 years to the value of the investment after 5 years is 25 : 36, then the minimum number of years required for the value of the investment to exceed Rs 20000 is
Ans: 9
Sol:
Thus, the minimum number of years required is 9 years (since t must be an integer).Hence, 9 is the required answer.
2023
Q1: Anil borrows Rs 2 lakhs at an interest rate of 8% per annum, compounded half-yearly. He repays Rs 10320 at the end of the first year and closes the loan by paying the outstanding amount at the end of the third year. Then, the total interest, in rupees, paid over the three years is nearest to [2023]
(a) 45311
(b) 51311
(c) 33130
(d) 40991
Ans: (b)
Sol:
The amount paid by Anil at the end of the third year = (2,00,000 × 1.042 − 10,320) × 1.044
= 2,40,990.8634
≅ 2,40,991
So the total amount paid by Anil = 10,320 + 2,40,991 = 2,51,311
So the total interest paid = 2,51,311 − 2,00,000 = 51,311
Q2: Anil invests Rs. 22000 for 6 years in a certain scheme with 4% interest per annum, compounded half-yearly. Sunil invests in the same scheme for 5 years, and then reinvests the entire amount received at the end of 5 years for one year at 10% simple interest. If the amounts received by both at the end of 6 years are same, then the initial investment made by Sunil, in rupees, is [2023]
Ans: 20808
Sol: “Anil invests Rs. 22000 for 6 years in a certain scheme with 4% interest per annum, compounded half-yearly.”
Total Amount of Anil’s investment after 6 years =Let Sunil Invest a Principal of P.
Sunil invests in the same scheme for 5 years, and then reinvests the entire amount received at the end of 5 years for one year at 10% simple interest.”
Total Amount of Sunil’s investment after 6 years =
Therefore, Sunil’s investment is Rs. 20808
2022
Q1: Nitu has an initial capital of ₹20,000. Out of this, she invests ₹8.000 at 5.5% in bank A, ₹5,000 at 5.6% in bank B and the remaining amount at x% in bank C, each rate being simple interest per annum. Her combined annual interest income from these investments is equal to 5% of the initial capital. If she had invested her entire initial capital in bank C alone, then her annual interest income, in rupees, would have been [2022]
(a) 900
(b) 700
(c) 1000
(d) 800
Ans: (d)
Sol: If Neetu intended to get a 5% annual interest, ideally all the banks should have maintained a 5% interest rate.
But Bank A returns 0.5% extra interest on 8000 rupees, which is 40 rupees.
But Bank B returns 0.6% extra interest on 5000 rupees, which is 30 rupees.
A & B combines are paying 70 rupees extra than 5%.
So Bank C should maintain such an interest rate that, the interest generated on the remaining 7000 rupees is 70 less than 5% interest.
Since 70 is 1% of 7000. The interest rate at Bank C should be 5% - 1% = 4%
If all the 20,000 rupees were invested in Bank C, the interest generated is 4% of 20,000 = 800 rupees.
Q2: Mr. Pinto invests one-fifth of his capital at 6%, one-third at 10% and the remaining at 1%, each rate being simple interest per annum. Then, the minimum number of years required for the cumulative interest income from these investments to equal or exceed his initial capital is
Ans: 20
Sol:
2021
Q1: Anil invests some money at a fixed rate of interest, compounded annually. If the interests accrued during the second and third year are ₹ 806.25 and ₹ 866.72, respectively, the interest accrued, in INR, during the fourth year is nearest to [2021]
(a) 929.48
(b) 934.65
(c) 931.72
(d) 926.84
Ans: (c)
Sol:
Let the principal amount be P and the interest rate be r.
ThenDividing (2) by (1), we get:
r = 0.075 or 7.5%
Dividing numerator and denominator by P(1 + r)2
Q2: Raj invested ₹ 10000 in a fund. At the end of first year, he incurred a loss but his balance was more than ₹ 5000. This balance, when invested for another year, grew and the percentage of growth in the second year was five times the percentage of loss in the first year. If the gain of Raj from the initial investment over the two year period is 35%, then the percentage of loss in the first year is [2021]
(a) 5
(b) 15
(c) 17
(d) 10
Ans: (d)
Sol:Raj invested Rs 10000 in the first year. Assuming the loss he faced was x%.
The amount after 1 year is 10,000 x (1 - x/100). = 10000 - 100*x.
Given the balance was greater than Rs 5000 and hence x < 50 percent.
When Raj invested this amount in the second year he earned a profit which is five times that of the first-year percentage.
Hence the amount after the second year is :Raj gained a total of 35 percent over the period of two years and hence the 35 percent is Rs 3500.
Hence the final amount is Rs 13,500.Solving the equation the roots are :
x = 10, x = 70.
Since x < 50, x = 10 percent.
Q3: Bank A offers 6% interest rate per annum compounded half-yearly. Bank B and Bank C offer simple interest but the annual interest rate offered by Bank C is twice that of Bank B. Raju invests a certain amount in Bank B for a certain period and Rupa invests ₹ 10,000 in Bank C for twice that period. The interest that would accrue to Raju during that period is equal to the interest that would have accrued had he invested the same amount in Bank A for one year. The interest accrued, in INR, to Rupa is [2021]
(a) 3436
(b) 2436
(c) 2346
(d) 1436
Ans: (b)
Sol:
Bank A: 6% p.a. 1/2 yearly (CI)
Bank B: x% p.a (SI)
Bank C: 2x% p.a (SI)
Let Raju invest Rs P in bank B for t years. Hence, Rupa invests Rs 10,000 in bank C for 2t years.
Now,We need to calculate
SI == 40000× 0.0609 = 2436
2020
Q1: Veeru invested Rs 10000 at 5% simple annual interest, and exactly after two years, Joy invested Rs 8000 at 10% simple annual interest. How many years after Veeru’s investment, will their balances, i.e., principal plus accumulated interest, be equal? [2020]
Ans: 12
Sol: Let after n years both the sums amount to the equal amounts.
Then,i.e.
Hence 12 years after veeru invested their balances will be equal.
Q2: For the same principal amount, the compound interest for two years at 5% per annum exceeds the simple interest for three years at 3% per annum by Rs 1125. Then the principal amount in rupees is [2020]
Ans: 90000
Sol: Let the principal be P.Given
⇒ P(0.1025 - 0.09) = 1125
⇒ P = 90, 000
Q3: A person invested a certain amount of money at 10% annual interest, compounded half-yearly. After one and a half years, the interest and principal together became Rs 18522. The amount, in rupees, that the person had invested is [2020]
Ans: 16000
Sol:
Let the sum be P.
Given,⇒
|
184 videos|212 docs|103 tests
|
FAQs on Simple & Compound Interest CAT Previous Year Questions with Answer PDF
| 1. What is the formula for calculating simple interest? |  |
| 2. How is compound interest different from simple interest? |  |
| 3. How can compound interest be calculated annually? |  |
| 4. Can compound interest be negative? |  |
| 5. What is the difference between nominal and effective interest rates in compound interest calculations? |  |