Games and Tournaments CAT Previous Year Questions with Answer PDF
2024
Direction: Answer the following questions based on the information given below.
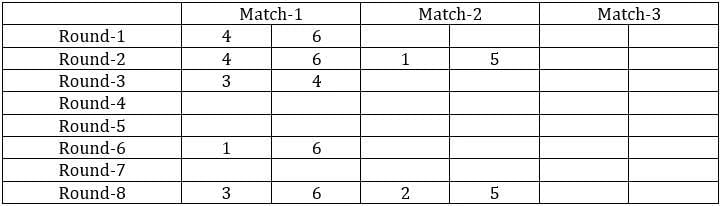
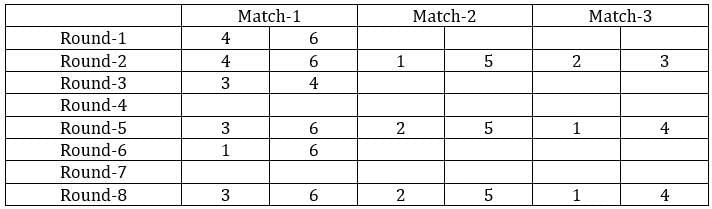
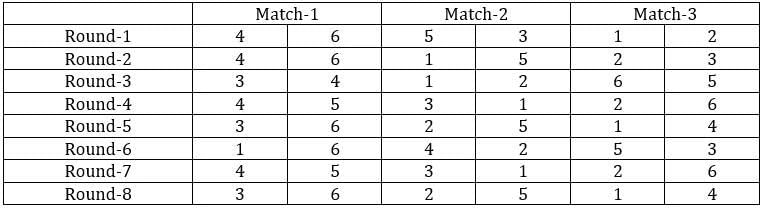
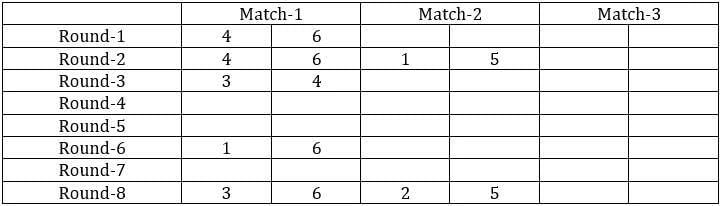
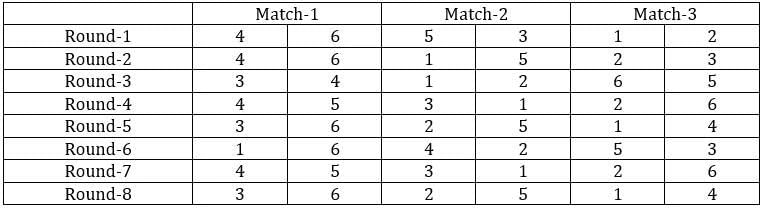
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
Q1: How many rounds were there in the tournament?
Ans: 8
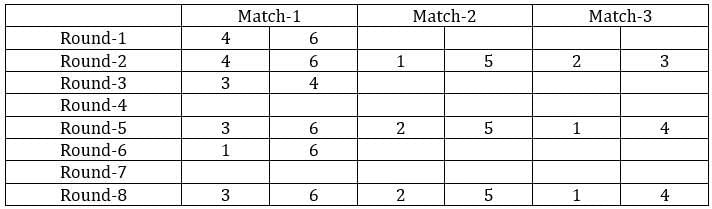
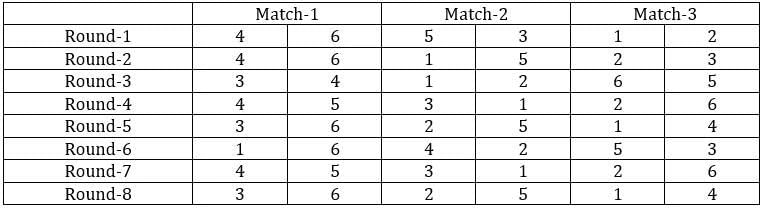
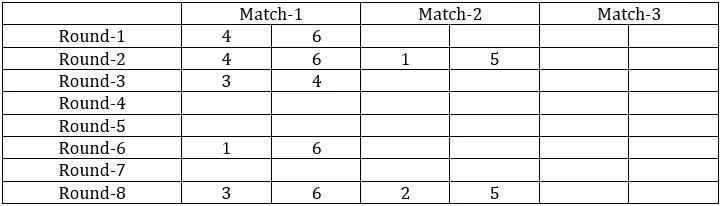
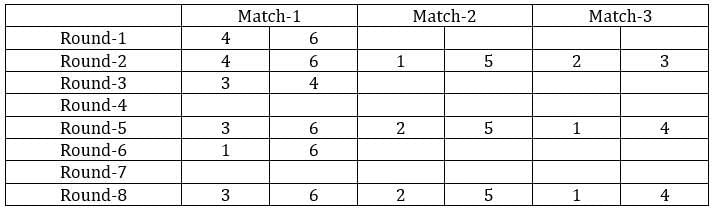
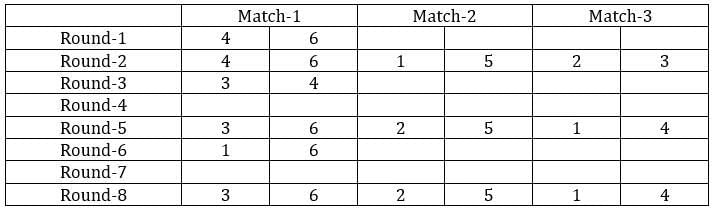
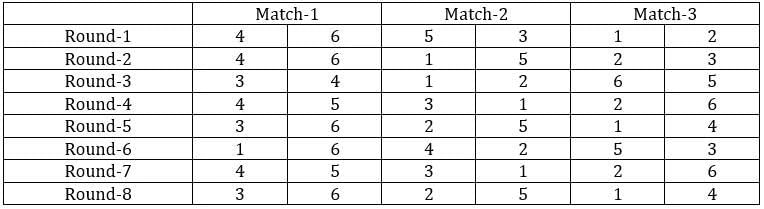
Sol: It is given that the six teams are divided into two groups and each team will play exactly one match with the team in their group and exactly two matches with the team in the opposite group. With this, we can say that there will be a total of 24 matches and a total of 8 rounds. We can make the following table with the given data.
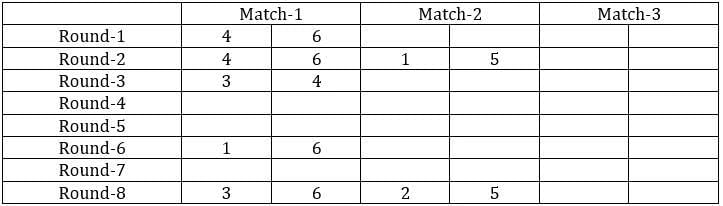
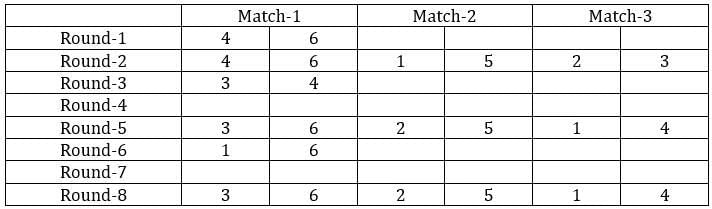
From the above table, we can say that Team 1 played Team 4 in round 8. Since in round 8, every team played against a team in the opposite group and since team 4 played two matches against team 6 and team 1 played only one match against team 5, we can say that teams 4, 3, and 2 belong to the same group and the teams 6, 1, and 5 belong to the same group.
We can fill in these details in the table.
Now from statement 2, we can say that the matches in the rounds 4 and 7 teams played against the teams that were not in the same group. With this, we can complete the table.
Q2: What is the number of the team that played Team 1 in Round 5?
Ans: 4
Sol: It is given that the six teams are divided into two groups and each team will play exactly one match with the team in their group and exactly two matches with the team in the opposite group. With this, we can say that there will be a total of 24 matches and a total of 8 rounds. We can make the following table with the given data.
From the above table, we can say that Team 1 played Team 4 in round 8. Since in round 8, every team played against a team in the opposite group and since team 4 played two matches against team 6 and team 1 played only one match against team 5, we can say that teams 4, 3, and 2 belong to the same group and the teams 6, 1, and 5 belong to the same group.
We can fill in these details in the table.
Now from statement 2, we can say that the matches in the rounds 4 and 7 teams played against the teams that were not in the same group. With this, we can complete the table.
Q3: Which team among the teams numbered 2, 3, 4, and 5 was not part of the same group?
(a) 3
(b) 2
(c) 4
(d) 5
Ans: d
Sol: It is given that the six teams are divided into two groups and each team will play exactly one match with the team in their group and exactly two matches with the team in the opposite group. With this, we can say that there will be a total of 24 matches and a total of 8 rounds. We can make the following table with the given data.
From the above table, we can say that Team 1 played Team 4 in round 8. Since in round 8, every team played against a team in the opposite group and since team 4 played two matches against team 6 and team 1 played only one match against team 5, we can say that teams 4, 3, and 2 belong to the same group and the teams 6, 1, and 5 belong to the same group.
We can fill in these details in the table.
Now from statement 2, we can say that the matches in the rounds 4 and 7 teams played against the teams that were not in the same group. With this, we can complete the table.
Q4: What is the number of the team that played Team 1 in Round 7?
Ans: 3
Sol: It is given that the six teams are divided into two groups and each team will play exactly one match with the team in their group and exactly two matches with the team in the opposite group. With this, we can say that there will be a total of 24 matches and a total of 8 rounds. We can make the following table with the given data.
From the above table, we can say that Team 1 played Team 4 in round 8. Since in round 8, every team played against a team in the opposite group and since team 4 played two matches against team 6 and team 1 played only one match against team 5, we can say that teams 4, 3, and 2 belong to the same group and the teams 6, 1, and 5 belong to the same group.
We can fill in these details in the table.
Now from statement 2, we can say that the matches in the rounds 4 and 7 teams played against the teams that were not in the same group. With this, we can complete the table.
Q5: What is the number of the team that played Team 6 in Round 3?
Ans: 5
Sol: It is given that the six teams are divided into two groups and each team will play exactly one match with the team in their group and exactly two matches with the team in the opposite group. With this, we can say that there will be a total of 24 matches and a total of 8 rounds. We can make the following table with the given data.
From the above table, we can say that Team 1 played Team 4 in round 8. Since in round 8, every team played against a team in the opposite group and since team 4 played two matches against team 6 and team 1 played only one match against team 5, we can say that teams 4, 3, and 2 belong to the same group and the teams 6, 1, and 5 belong to the same group.
We can fill in these details in the table.
Now from statement 2, we can say that the matches in the rounds 4 and 7 teams played against the teams that were not in the same group. With this, we can complete the table.
2023
Passage
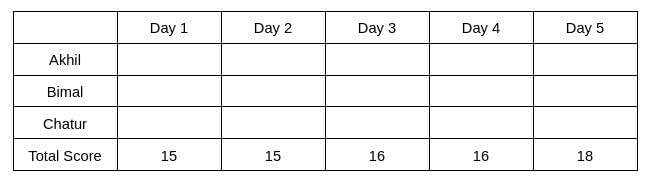
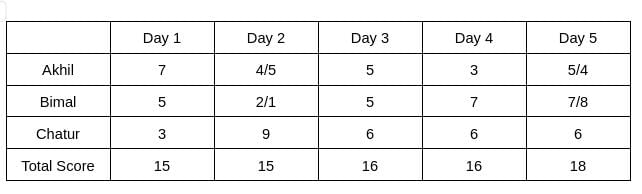
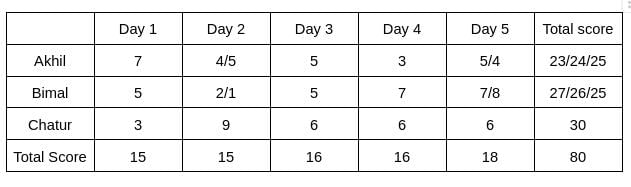
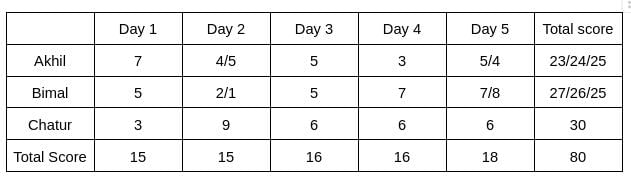
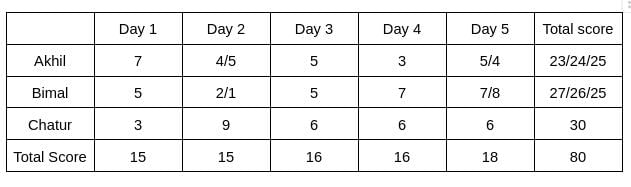
Three participants – Akhil, Bimal and Chatur participate in a random draw competition for five days. Every day, each participant randomly picks up a ball numbered between 1 and 9. The number on the ball determines his score on that day. The total score of a participant is the sum of his scores attained in the five days. The total score of a day is the sum of participants' scores on that day. The 2-day average on a day, except on Day 1, is the average of the total scores of that day and of the previous day. For example, if the total scores of Day 1 and Day 2 are 25 and 20, then the 2-day average on Day 2 is calculated as 22.5. Table 1 gives the 2-day averages for Days 2 through 5.
Participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. If there is a tie, all participants with the tied score are awarded the best available rank. For example, if on a day Akhil, Bimal, and Chatur score 8, 7 and 7 respectively, then their ranks will be 1, 2 and 2 respectively on that day. These ranks are given in Table 2.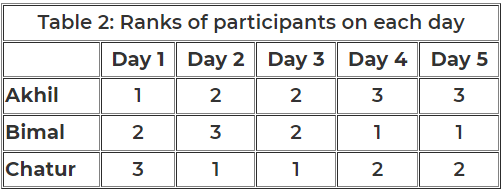 The following information is also known.
The following information is also known.
1. Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil's score on Day 4.
2. The total score on Day 3 is the same as the total score on Day 4.
3. Bimal's scores are the same on Day 1 and Day 3. [2023]
Q1: What is Akhil's score on Day 1?
A: 5
B: 7
C: 6
D: 8
Ans: B
Sol:
Let the total score of day 1, day 2, day 3, day 4, and day 5 are d1, d2, d3, d4, and d5, respectively.
The table shows that d1+d2 = 30 ... eq (1), d2+d3 = 31 ... eq (2), d3+d4 = 32 .... eq(3), d4+d5 = 34 ... eq(4)
It is given that participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. All participants with a tied score are awarded the best available rank if there is a tie.
It is given that the total score on Day 3 is the same as the total score on Day 4.
Therefore, d3 = d4 => d3 = d4 = 16, which implies d2 = 15, d5 = 18, and d1 = 15.
The day-wise score is given below:
It is known that Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil’s score on Day 4.
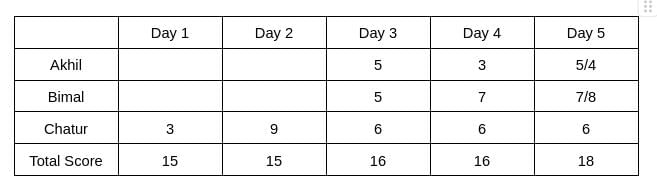
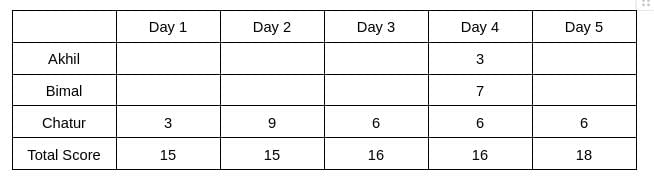
Hence, only Chatur scored 9 (one time) on Day 2, and no other person scored 9 on any of the given 5 days. Chatur scored 3 only one time, which was on Day 1. Therefore, the scores obtained by Chatur on Day 3, Day 4, and Day 5 are 6, 6, and 6, respectively. It is also known that Akhil's score on Day 4 is the same as the score obtained by Chatur on Day 1. Hence, Akhil's score on Day 4 is 3.
Hence, we get the following table:
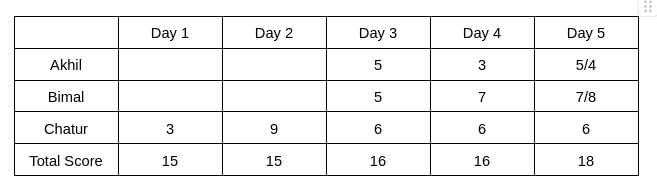
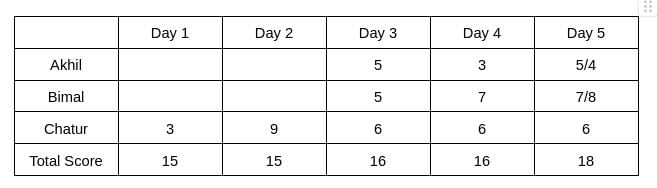
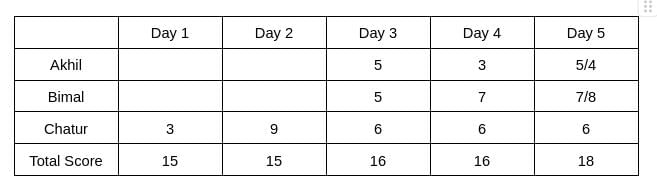
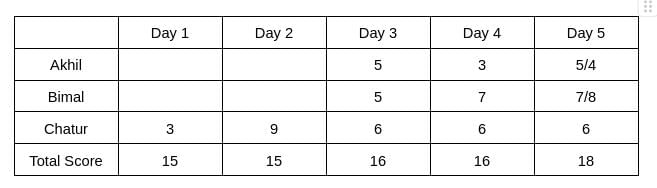
From Table 2, we see that the rank of Bimal and Akhil is the same, which is 2. Hence, The score obtained by Akhil and Bimal is the same. Let the score be x. Therefore, 6+2x = 16 => x = 5
The rank of Chatur on Day 5 is 2, and the rank of Bimal is 1, which implies the score obtained by Bimal will be more than Chatur. Hence, Bimal can score either 7 or 8 on Day 5. Therefore, the score obtained by Akhil on Day 5 is either 5 or 4.
It is given that Bimal’s scores are the same on Day 1 and Day 3. Hence, the score obtained by Bimal on Day 1 is 5, which implies The score obtained by Akhil is 7 on Day 1.
From Table 2, we can see that the rank of Bimal is 3 on Day 2, and the rank of Akhil is 2 on Day 2. Hence, the score of Bimal will be lower than Akhil on Day 2.
Let the score of Akhil be a, and the score of Bimal be b. Then 9+a+b = 15, and a > b
=> a+b =6, and a> b
Hence, the value of a can be 4/5, and the value of b can be 2/1
Therefore, the final table is given below:
From the table, we can see that the score of Akhil is 7 on day 1.
The correct option is B
Q2: Who attains the maximum total score?
A: Chatur
B: Akhil
C: Bimal
D: Cannot be determined
Ans: A
Sol:Let the total score of day 1, day 2, day 3, day 4, and day 5 are d1, d2, d3, d4, and d5, respectively.
The table shows that d1+d2 = 30 ... eq (1), d2+d3 = 31 ... eq (2), d3+d4 = 32 .... eq(3), d4+d5 = 34 ... eq(4)
It is given that participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. All participants with a tied score are awarded the best available rank if there is a tie.
It is given that the total score on Day 3 is the same as the total score on Day 4.
Therefore, d3 = d4 => d3 = d4 = 16, which implies d2 = 15, d5 = 18, and d1 = 15.
The day-wise score is given below:
It is known that Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil’s score on Day 4.
Hence, only Chatur scored 9 (one time) on Day 2, and no other person scored 9 on any of the given 5 days. Chatur scored 3 only one time, which was on Day 1. Therefore, the scores obtained by Chatur on Day 3, Day 4, and Day 5 are 6, 6, and 6, respectively. It is also known that Akhil's score on Day 4 is the same as the score obtained by Chatur on Day 1. Hence, Akhil's score on Day 4 is 3.
Hence, we get the following table:
From Table 2, we see that the rank of Bimal and Akhil is the same, which is 2. Hence, The score obtained by Akhil and Bimal is the same. Let the score be x. Therefore, 6+2x = 16 => x = 5
The rank of Chatur on Day 5 is 2, and the rank of Bimal is 1, which implies the score obtained by Bimal will be more than Chatur. Hence, Bimal can score either 7 or 8 on Day 5. Therefore, the score obtained by Akhil on Day 5 is either 5 or 4.
It is given that Bimal’s scores are the same on Day 1 and Day 3. Hence, the score obtained by Bimal on Day 1 is 5, which implies The score obtained by Akhil is 7 on Day 1.
From Table 2, we can see that the rank of Bimal is 3 on Day 2, and the rank of Akhil is 2 on Day 2. Hence, the score of Bimal will be lower than Akhil's on Day 2.
Let the score of Akhil be a, and the score of Bimal be b. Then 9+a+b = 15, and a > b
=> a+b =6, and a> b
Hence, the value of a can be 4/5, and the value of b can be 2/1
Therefore, the final table is given below:
From the table, we can see that the maximum score is obtained by Chatur.
The correct option is A
Q3: What is the minimum possible total score of Bimal?
Ans: 25
Sol:Let the total score of day 1, day 2, day 3, day 4, and day 5 are d1, d2, d3, d4, and d5, respectively.
The table shows that d1+d2 = 30 ... eq (1), d2+d3 = 31 ... eq (2), d3+d4 = 32 .... eq(3), d4+d5 = 34 ... eq(4)
It is given that participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. All participants with a tied score are awarded the best available rank if there is a tie.
It is given that the total score on Day 3 is the same as the total score on Day 4.
Therefore, d3 = d4 => d3 = d4 = 16, which implies d2 = 15, d5 = 18, and d1 = 15.
The day-wise score is given below:
It is known that Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil’s score on Day 4.
Hence, only Chatur scored 9 (one time) on Day 2, and no other person scored 9 on any of the given 5 days. Chatur scored 3 only one time, which was on Day 1. Therefore, the scores obtained by Chatur on Day 3, Day 4, and Day 5 are 6, 6, and 6, respectively. It is also known that Akhil's score on Day 4 is the same as the score obtained by Chatur on Day 1. Hence, Akhil's score on Day 4 is 3.
Hence, we get the following table:
From Table 2, we see that the rank of Bimal and Akhil is the same, which is 2. Hence, The score obtained by Akhil and Bimal is the same. Let the score be x. Therefore, 6+2x = 16 => x = 5
The rank of Chatur on Day 5 is 2, and the rank of Bimal is 1, which implies the score obtained by Bimal will be more than Chatur. Hence, Bimal can score either 7 or 8 on Day 5. Therefore, the score obtained by Akhil on Day 5 is either 5 or 4.
It is given that Bimal’s scores are the same on Day 1 and Day 3. Hence, the score obtained by Bimal on Day 1 is 5, which implies The score obtained by Akhil is 7 on Day 1.
From Table 2, we can see that the rank of Bimal is 3 on Day 2, and the rank of Akhil is 2 on Day 2. Hence, the score of Bimal will be lower than Akhil on Day 2.
Let the score of Akhil be a, and the score of Bimal be b. Then 9+a+b = 15, and a > b
=> a+b =6, and a> b
Hence, the value of a can be 4/5, and the value of b can be 2/1
Therefore, the final table is given below:
From the table, we can see that the minimum score obtained by Bimal is 25.
Q4: If the total score of Bimal is a multiple of 3, what is the score of Akhil on Day 2?
A: 4
B: 6
C: 5
D: Cannot be determined
Ans: A
Sol:
Let the total score of day 1, day 2, day 3, day 4, and day 5 are d1, d2, d3, d4, and d5, respectively.
The table shows that d1+d2 = 30 ... eq (1), d2+d3 = 31 ... eq (2), d3+d4 = 32 .... eq(3), d4+d5 = 34 ... eq(4)
It is given that participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. All participants with a tied score are awarded the best available rank if there is a tie.
It is given that the total score on Day 3 is the same as the total score on Day 4.
Therefore, d3 = d4 => d3 = d4 = 16, which implies d2 = 15, d5 = 18, and d1 = 15.
The day-wise score is given below:
It is known that Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil’s score on Day 4.
Hence, only Chatur scored 9 (one time) on Day 2, and no other person scored 9 on any of the given 5 days. Chatur scored 3 only one time, which was on Day 1. Therefore, the scores obtained by Chatur on Day 3, Day 4, and Day 5 are 6, 6, and 6, respectively. It is also known that Akhil's score on Day 4 is the same as the score obtained by Chatur on Day 1. Hence, Akhil's score on Day 4 is 3.
Hence, we get the following table:
From Table 2, we see that the rank of Bimal and Akhil is the same, which is 2. Hence, The score obtained by Akhil and Bimal is the same. Let the score be x. Therefore, 6+2x = 16 => x = 5
The rank of Chatur on Day 5 is 2, and the rank of Bimal is 1, which implies the score obtained by Bimal will be more than Chatur. Hence, Bimal can score either 7 or 8 on Day 5. Therefore, the score obtained by Akhil on Day 5 is either 5 or 4.
It is given that Bimal’s scores are the same on Day 1 and Day 3. Hence, the score obtained by Bimal on Day 1 is 5, which implies The score obtained by Akhil is 7 on Day 1.
From Table 2, we can see that the rank of Bimal is 3 on Day 2, and the rank of Akhil is 2 on Day 2. Hence, the score of Bimal will be lower than Akhil on Day 2.
Let the score of Akhil be a, and the score of Bimal be b. Then 9+a+b = 15, and a > b
=> a+b =6, and a> b
Hence, the value of a can be 4/5, and the value of b can be 2/1
Therefore, the final table is given below:
In the question, it is given that the total score obtained by Bimal is a multiple of 3, which implies the total score obtained by Bimal is 27, which implies the total score obtained by Akhil is 23.
Akhil will score 23, when his scores on Days 1, 2, 3, 4, and 5 are 7, 4, 5, 3, 4, respectively.
Hence, the score obtained by him on Day 2 is 4.
The correct option is A
Q5: If Akhil attains a total score of 24, then what is the total score of Bimal?
Ans: 26
Sol:Let the total score of day 1, day 2, day 3, day 4, and day 5 are d1, d2, d3, d4, and d5, respectively.
The table shows that d1+d2 = 30 ... eq (1), d2+d3 = 31 ... eq (2), d3+d4 = 32 .... eq(3), d4+d5 = 34 ... eq(4)
It is given that participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. All participants with a tied score are awarded the best available rank if there is a tie.
It is given that the total score on Day 3 is the same as the total score on Day 4.
Therefore, d3 = d4 => d3 = d4 = 16, which implies d2 = 15, d5 = 18, and d1 = 15.
The day-wise score is given below:
It is known that Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil’s score on Day 4.
Hence, only Chatur scored 9 (one time) on Day 2, and no other person scored 9 on any of the given 5 days. Chatur scored 3 only one time, which was on Day 1. Therefore, the scores obtained by Chatur on Day 3, Day 4, and Day 5 are 6, 6, and 6, respectively. It is also known that Akhil's score on Day 4 is the same as the score obtained by Chatur on Day 1. Hence, Akhil's score on Day 4 is 3.
Hence, we get the following table:
From Table 2, we see that the rank of Bimal and Akhil is the same, which is 2. Hence, The score obtained by Akhil and Bimal is the same. Let the score be x. Therefore, 6+2x = 16 => x = 5
The rank of Chatur on Day 5 is 2, and the rank of Bimal is 1, which implies the score obtained by Bimal will be more than Chatur. Hence, Bimal can score either 7 or 8 on Day 5. Therefore, the score obtained by Akhil on Day 5 is either 5 or 4.
It is given that Bimal’s scores are the same on Day 1 and Day 3. Hence, the score obtained by Bimal on Day 1 is 5, which implies The score obtained by Akhil is 7 on Day 1.
From Table 2, we can see that the rank of Bimal is 3 on Day 2, and the rank of Akhil is 2 on Day 2. Hence, the score of Bimal will be lower than Akhil on Day 2.
Let the score of Akhil be a, and the score of Bimal be b. Then 9+a+b = 15, and a > b
=> a+b =6, and a> b
Hence, the value of a can be 4/5, and the value of b can be 2/1
Therefore, the final table is given below:
In the question, it is given that the score obtained by Akhil is 24, which implies the score obtained by Bimal is 26.
The answer is 26
2022
Passage
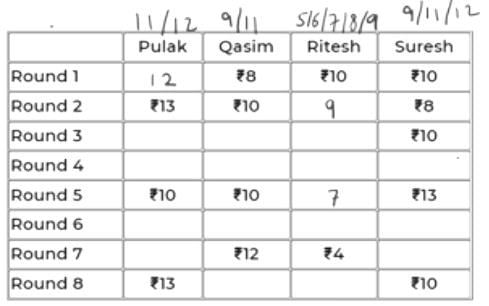
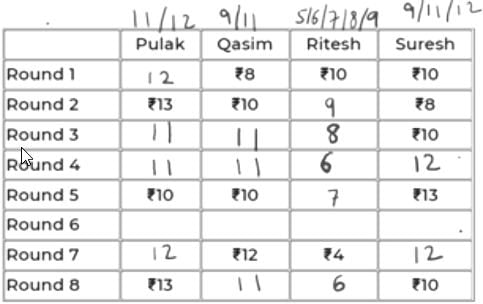
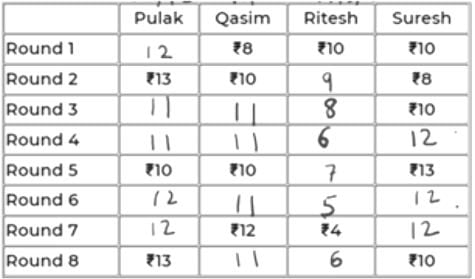
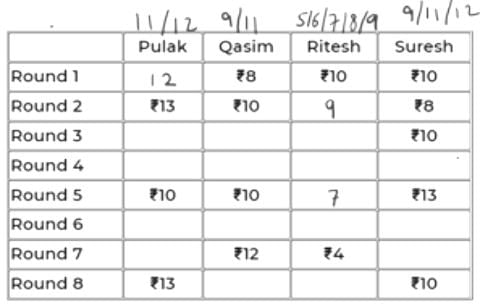
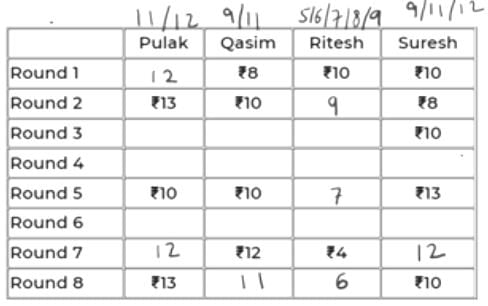
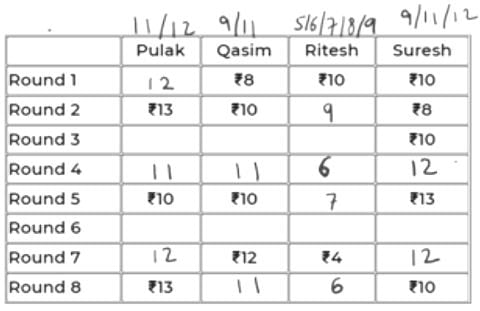
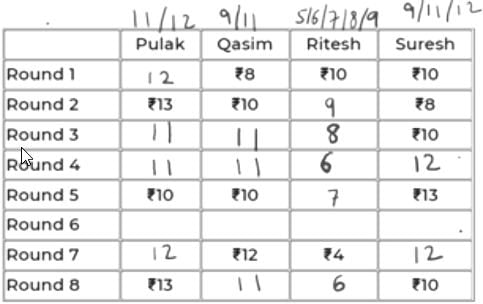
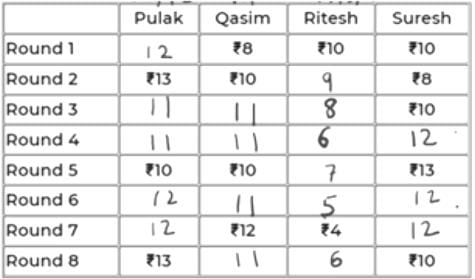
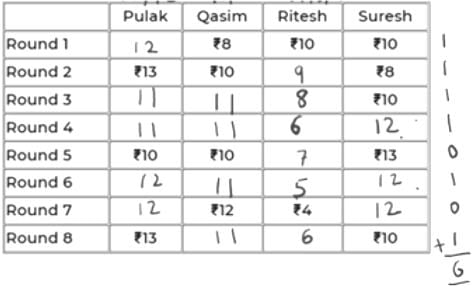
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game.
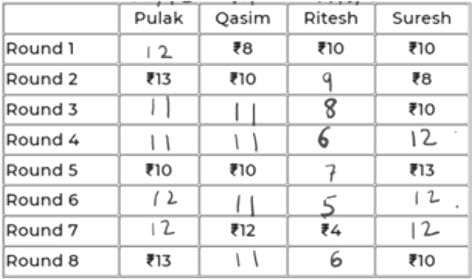
At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eight rounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3, and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.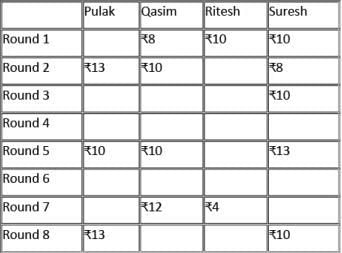
Q1: What BEST can be said about the amount of money that Ritesh had with him at the end of Round 8?
(a) ₹4 or ₹5
(b) Exactly ₹5
(c) Exactly ₹6
(d) ₹5 or ₹6
Ans: c
Sol:
We will denote the 4 players by their initials for ease, i.e., P, Q, R & S.
Since, the highest, lowest and exactly Rs. 10 amounts are given in the table for each player, we can conclude that in the remaining rounds,
P – 11/12
Q – 9/11
R – 5/6/7/8/9
S – 9/11/12
All of them start with an initial amount of Rs. 10 and in each round, the net sum of amounts remains constant, i.e., 40.
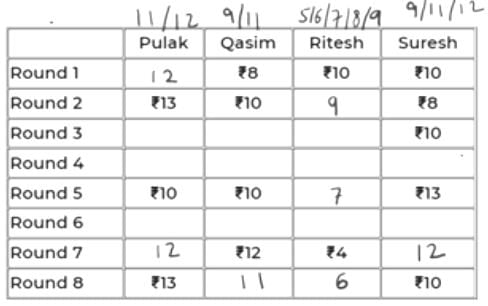
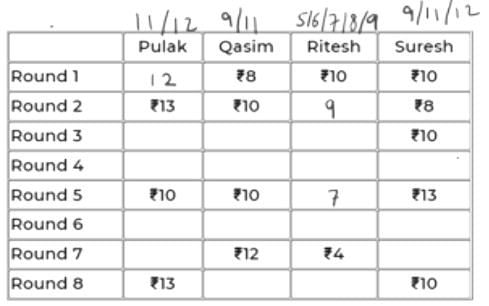
Using this information, we can conclude:
In the 7th round, if P has 11 (+2 in 8th round), then S must have 40-(11+12+4) = 13 (-3 in 8th round).
=> +3 will be for R (+3 = 15 not possible for Q as max is 12) and -2 for Q in 8th round. But 12-2 = 10 and if this were a valid case, then 10 must have been already given in the table.
So, we can conclude that in the 7th round, P has 12 and S has 12.
In 8th round, +1 for P, -2 for S. We can’t have +2 for Q as 14 is not possible. So, we have +2 for R and -1 for Q in Rd 8.
So, scores of P, Q, R, S in the 8th round are 13, 11, 6, 10.
The table looks like below now.
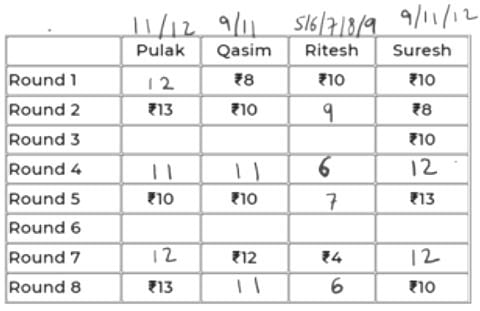
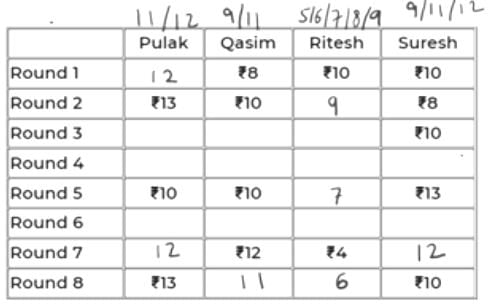
It is given that P and Q have same amount at the end of Rd 4. That amount can only be 11 as the common of 11, 12 and 9, 11 is 11.
11 to 10 is -1 (from Rd 4 to 5). So, R and S must have had +1 each in Rd 5. So, their scores in Rd 4 must be 6 and 12 respectively.
The updated table is:
Now, in Rd 3, Q’s amount can only be 11 because having 9 would mean -1 from Rd 2 to 3.
=> Someone should have +1 in Rd 3. But neither P can have 14, nor R can have 10.
Hence, Q has 11 in Rd 3 and Rd 4. So, P must also have 11 in Rd 3 as R cannot have 6 in Rd 3. So, R will have 8 in Rd 3.
The updated table is:
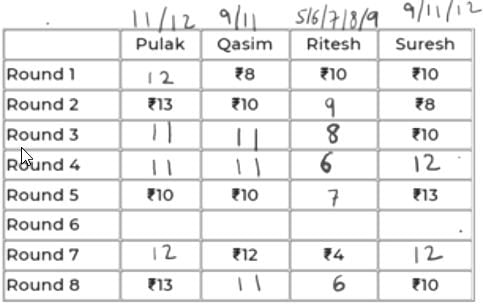
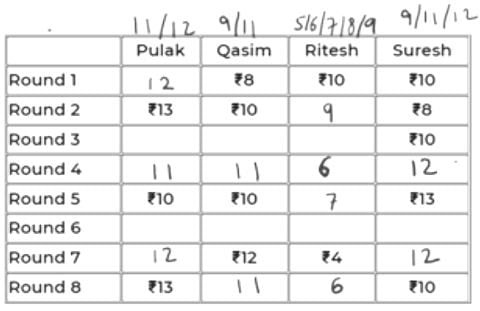
In Rd 6, Q can only have 11 because if it has 9, then 9 to 12 wouldn’t be possible in Rd 7 as max exchange is of Rs. 2.
Now, R will be either 5 or 6 in Rd 6 as it has to eventually be 4 in Rd 7.
If R were 6 in Rd 6, i.e., -2 in Rd 7, someone will have to be +2 in Rd 7. This can’t be P because 12-2 = 10 and had it been 10 in Rd 6, it would have been given. S also cannot be 10 in Rd 6 as 13 to 10 is not possible in Rd 6.
So, R has 5 in Rd 6.
The final table is:
So, R had exactly Rs. 6 at the end of Rd 8.
Q2: What BEST can be said about the amount of money that Pulak had with him at the end of Round 6?
(a) Exactly ₹12
(b) ₹11 or ₹12
(c) ₹12 or ₹13
(d) Exactly ₹11
Ans: a
Sol:
We will denote the 4 players by their initials for ease, i.e., P, Q, R & S.
Since, the highest, lowest and exactly Rs. 10 amounts are given in the table for each player, we can conclude that in the remaining rounds,
P – 11/12
Q – 9/11
R – 5/6/7/8/9
S – 9/11/12
All of them start with an initial amount of Rs. 10 and in each round, the net sum of amounts remains constant, i.e., 40.
Using this information, we can conclude:
In the 7th round, if P has 11 (+2 in 8th round), then S must have 40-(11+12+4) = 13 (-3 in 8th round).
=> +3 will be for R (+3 = 15 not possible for Q as max is 12) and -2 for Q in 8th round. But 12-2 = 10 and if this were a valid case, then 10 must have been already given in the table.
So, we can conclude that in the 7th round, P has 12 and S has 12.
In 8th round, +1 for P, -2 for S. We can’t have +2 for Q as 14 is not possible. So, we have +2 for R and -1 for Q in Rd 8.
So, scores of P, Q, R, S in the 8th round are 13, 11, 6, 10.
The table looks like below now.
It is given that P and Q have same amount at the end of Rd 4. That amount can only be 11 as the common of 11, 12 and 9, 11 is 11.
11 to 10 is -1 (from Rd 4 to 5). So, R and S must have had +1 each in Rd 5. So, their scores in Rd 4 must be 6 and 12 respectively.
The updated table is:
Now, in Rd 3, Q’s amount can only be 11 because having 9 would mean -1 from Rd 2 to 3.
=> Someone should have +1 in Rd 3. But neither P can have 14, nor R can have 10.
Hence, Q has 11 in Rd 3 and Rd 4. So, P must also have 11 in Rd 3 as R cannot have 6 in Rd 3. So, R will have 8 in Rd 3.
The updated table is:
In Rd 6, Q can only have 11 because if it has 9, then 9 to 12 wouldn’t be possible in Rd 7 as max exchange is of Rs. 2.
Now, R will be either 5 or 6 in Rd 6 as it has to eventually be 4 in Rd 7.
If R were 6 in Rd 6, i.e., -2 in Rd 7, someone will have to be +2 in Rd 7. This can’t be P because 12-2 = 10 and had it been 10 in Rd 6, it would have been given. S also cannot be 10 in Rd 6 as 13 to 10 is not possible in Rd 6.
So, R has 5 in Rd 6.
The final table is:
Based on the calculations in Q6, Pulak had exactly Rs. 12 at the end of Rd 6.
Q3: How much money (in ₹) did Ritesh have at the end of Round 4?
Ans: 6
Sol:
We will denote the 4 players by their initials for ease, i.e., P, Q, R & S.
Since, the highest, lowest and exactly Rs. 10 amounts are given in the table for each player, we can conclude that in the remaining rounds,
P – 11/12
Q – 9/11
R – 5/6/7/8/9
S – 9/11/12
All of them start with an initial amount of Rs. 10 and in each round, the net sum of amounts remains constant, i.e., 40.
Using this information, we can conclude:
In the 7th round, if P has 11 (+2 in 8th round), then S must have 40-(11+12+4) = 13 (-3 in 8th round).
=> +3 will be for R (+3 = 15 not possible for Q as max is 12) and -2 for Q in 8th round. But 12-2 = 10 and if this were a valid case, then 10 must have been already given in the table.
So, we can conclude that in the 7th round, P has 12 and S has 12.
In 8th round, +1 for P, -2 for S. We can’t have +2 for Q as 14 is not possible. So, we have +2 for R and -1 for Q in Rd 8.
So, scores of P, Q, R, S in the 8th round are 13, 11, 6, 10.
The table looks like below now.
It is given that P and Q have same amount at the end of Rd 4. That amount can only be 11 as the common of 11, 12 and 9, 11 is 11.
11 to 10 is -1 (from Rd 4 to 5). So, R and S must have had +1 each in Rd 5. So, their scores in Rd 4 must be 6 and 12 respectively.
The updated table is:
Now, in Rd 3, Q’s amount can only be 11 because having 9 would mean -1 from Rd 2 to 3.
=> Someone should have +1 in Rd 3. But neither P can have 14, nor R can have 10.
Hence, Q has 11 in Rd 3 and Rd 4. So, P must also have 11 in Rd 3 as R cannot have 6 in Rd 3. So, R will have 8 in Rd 3.
The updated table is:
In Rd 6, Q can only have 11 because if it has 9, then 9 to 12 wouldn’t be possible in Rd 7 as max exchange is of Rs. 2.
Now, R will be either 5 or 6 in Rd 6 as it has to eventually be 4 in Rd 7.
If R were 6 in Rd 6, i.e., -2 in Rd 7, someone will have to be +2 in Rd 7. This can’t be P because 12-2 = 10 and had it been 10 in Rd 6, it would have been given. S also cannot be 10 in Rd 6 as 13 to 10 is not possible in Rd 6.
So, R has 5 in Rd 6.
The final table is:
Based on the calculations in Q6, Ritesh had Rs. 6 at the end of Rd 4.
Q4: How many games were played with a bet of ₹2?
Ans: 6
Sol:
There were 6 games played with a bet of Rs. 2.
Q5: Which of the following pairings was made in Round 5?
(a) Pulak and Ritesh
(b) Pulak and Qasim
(c) Pulak and Suresh
(d) Qasim and Suresh
Ans: c
Sol:
In Rd 4, PQ and RS were the pairs.
In Rd 6, PR and QS were the pairs.
So, in Rd 5, PS and QR must have been the pairs, i.e., Pulak & Suresh.
2021
Passage
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
- Aruna did not play against Arif. Brij did not play against Brinda.
- Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
- Chitra did not win the championship.
Q1: Who among the following was DEFINITELY NOT ranked first in his/her group?
(a) Dipen
(b) Aruna
(c) Brij
(d) Chitra
Ans: a
Sol: Dipen was ranked 2 or 3 in his group
Q2: Which of the following pairs must have played against each other in the championship?
(a) Deb, Donna
(b) Azul, Biju
(c) Donna, Chetan
(d) Chitra, Dipen
Ans: d
Sol: hitra and Dipen played in the semifinals
Q3: Who won the championship?
(a) Chitra
(b) Aruna
(c) Brij
(d) Cannot be determined
Ans: b
Sol: runa is the winner.
Q4: Who among the following did NOT play against Chitra in the championship?
(a) Aruna
(b) Chetan
(c) Dipen
(d) Biju
Ans: d
Sol: rij was the player from group B who played Chitra. Aruna played in finals, Chetan in round 2, and Dipen in semi finals
2020
Passage
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
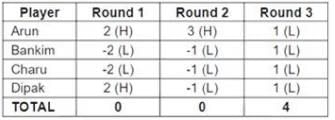
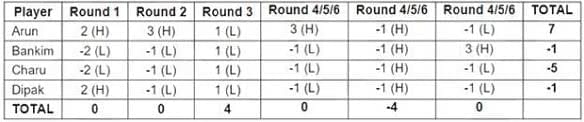
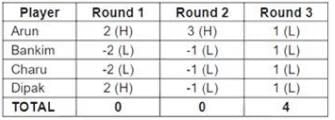
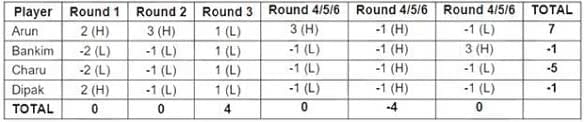
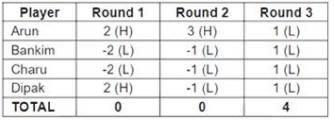
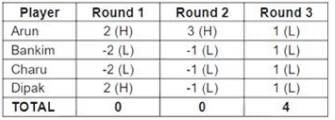
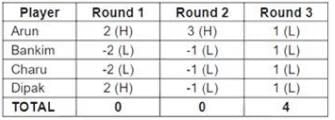
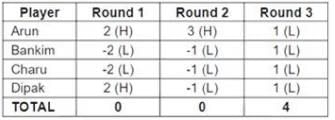
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Q1: What were the bids by Arun, Bankim, Charu and Dipak, respectively in the first round?
A: Hi, Lo, Lo, Lo
B: Lo, Lo, Lo, Hi
C: Hi, Hi, Lo, Lo
D: Hi, Lo, Lo, Hi
Ans: D
Sol:
From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (- 4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, - 1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
Since Arun scored a total of 6 points in the first three rounds, and he scored 3 points and 1 point in two of these rounds, he must have score 2 points in the other round. This is possible only if the players bid HHLL and the scores of the four players must be (2, 2, - 2, - 2).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
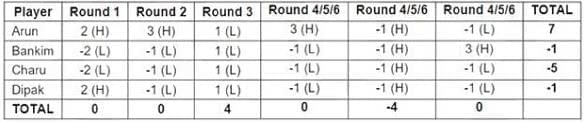
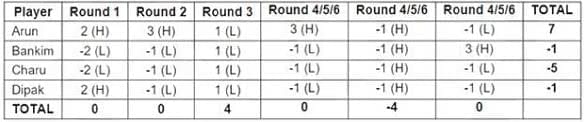
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1).
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
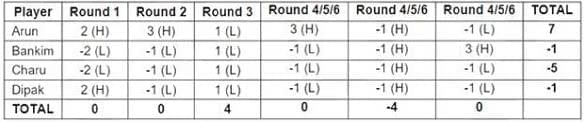
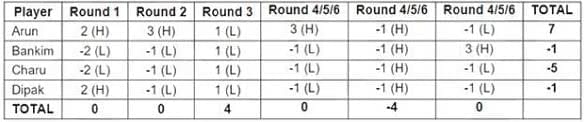
Hence, we get the following table:
The bids by Arun, Bankim, Charu, Dipak in the first round were Hi, Lo, Lo, Hi.
Q2: In how many rounds did Bankim bid Lo?
Ans: 4
Sol:
From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (- 4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, - 1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
Since Arun scored a total of 6 points in the first three rounds, and he scored 3 points and 1 point in two of these rounds, he must have score 2 points in the other round. This is possible only if the players bid HHLL and the scores of the four players must be (2, 2, - 2, - 2).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1).
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
Bankim bid Lo in 4 rounds
Q3: In how many rounds did Dipak gain exactly 1 point?
Ans: 1
Sol:
From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (- 4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, - 1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
Since Arun scored a total of 6 points in the first three rounds, and he scored 3 points and 1 point in two of these rounds, he must have score 2 points in the other round. This is possible only if the players bid HHLL and the scores of the four players must be (2, 2, - 2, - 2).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1).
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
Dipak gained exactly 1 point in 1 round
Q4: In how many rounds did Arun bid Hi?
Ans: 4
Sol:
From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (- 4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, - 1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
Since Arun scored a total of 6 points in the first three rounds, and he scored 3 points and 1 point in two of these rounds, he must have score 2 points in the other round. This is possible only if the players bid HHLL and the scores of the four players must be (2, 2, - 2, - 2).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1).
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
Arun bid Hi in 4 rounds
Q5: In how many rounds did all four players make identical bids?
Ans: 2
Sol:
From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (- 4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, - 1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
Since Arun scored a total of 6 points in the first three rounds, and he scored 3 points and 1 point in two of these rounds, he must have score 2 points in the other round. This is possible only if the players bid HHLL and the scores of the four players must be (2, 2, - 2, - 2).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1).
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
All four players made identical bids in 2 rounds
Q6: In which of the following rounds, was Arun DEFINITELY the only player to bid Hi?
A: First
B: Fourth
C: Third
D: Second
Ans: D
Sol:
From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (- 4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, - 1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
Since Arun scored a total of 6 points in the first three rounds, and he scored 3 points and 1 point in two of these rounds, he must have score 2 points in the other round. This is possible only if the players bid HHLL and the scores of the four players must be (2, 2, - 2, - 2).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1).
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
In the second round, Arun was the only player to bid Hi.
|
77 videos|180 docs|96 tests
|
FAQs on Games and Tournaments CAT Previous Year Questions with Answer PDF
| 1. What are the different types of game theory in tournaments? |  |
| 2. How are tournaments structured in game theory? |  |
| 3. What is the significance of Nash equilibrium in tournament games? |  |
| 4. How do players strategize in tournament games to maximize their chances of winning? |  |
| 5. Can game theory be applied to real-life tournaments and competitions? |  |