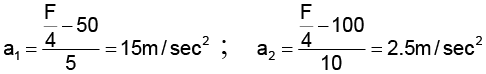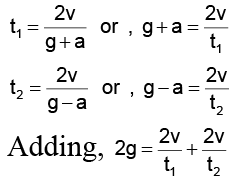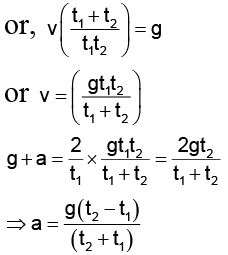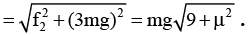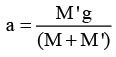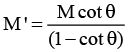JEE Advanced (One or More Correct Option): Laws of Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download

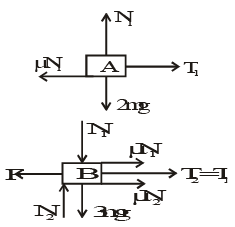
Q.1. Co-efficient of friction for all surfaces is μ. The strings and pulleys are ideal. Blocks are moving at a constant speed. Choose the correct options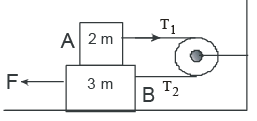
(a) F = 9μmg
(b) T₁ = 2μmg
(c) T₂ = 6μmg
(d) T₁ = 4μmg

Correct Answer is Option (a and b)

As string is ideal T₁ = T₂
T₁ = μN₁ = 2 μmg
F = T₁ + μN₁ + μN₂ = 2 μmg + 2μmg + 5μmg = 9 μmg.

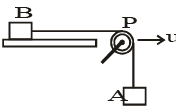
Q.2. In the figure, the pulley P moves to the right with a constant speed u. The downward speed of A is 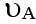, and the speed of B to the right is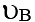
(a)
(b)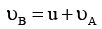 
(c)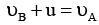 
(d) the two blocks have accelerations of the same magnitude.

Correct Answer is option (b and d)
At any instant of time, let the length of the string BP = l₁ and the length PA = l₂. In a further time t, let B move to the right by x and A move down by y, while P moves to the right by ut. As the length of the string must remain constant,
l₁ + l₂ = (l₁ – x + ut) + (l₂ + y)
or x = ut + y
or x. = u + y. .

x = speed of B to the right = v_B, .

y = downward speed of A = v_A
∴ v_B = u + v_A

Also, v.B =vA
or, a_B = a_A.

Q.3.  A block of mass m₁ is connected with another block of mass m2 by a light unextended spring kept on a smooth horizontal plane. m₂ is connected with a hanging mass m3 by an inextensible light string. At the time of release of block m₃: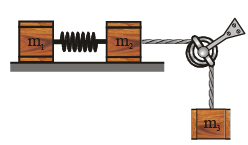
(a) tension in the string is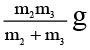
(b) acceleration of m₁ is zero
(c) acceleration of m₂ is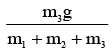
(d) acceleration of m₂ is

Correct Answer is option (A, b and d)
Initially spring is unstretched

Q.4. Two masses A and B lie on a frictionless table. They are attached to either end of a light rope which passes around a horizontal movable pulley of negligible mass.
mA = 1 kg, m_B = 2 kg, m_c = 4 kg. Pulley P₂ is vertical.

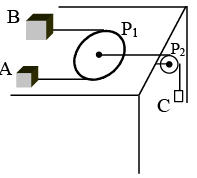(a) a_A = 8 m/s²
(b) a_B = 4 m/s²
(c) a_c = 6 m/s²
(d) a_A > a_B > a_C

Correct Answer is option (A, b and c)

FBD of A and  B
w.r.t. pulley P₁
Equations of motion are
T – 2a_c = 2a₁ …(i)
a_c – T = a₁ …(ii)
and 40 – 2T = 4a …(iii)
Solve to get the answers.

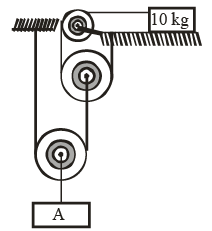
Q.5. The acceleration of blocks of masses 5 kg and 10 kg are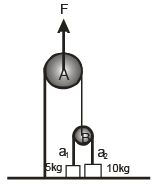
(a) zero if F = 100N
(b) a₁ = 5m / s² and a₂ = 0 if F = 300N
(c) a₁ = 15m /s² a₂ = 2.5m / s² if F = 500N
(d) Acceleration of the masses is independent of F

Correct Answer is option (A, b and c)

2T ' = F ;  T' F/2 = ; 2T = T'= F/ 2; T = F/ 4

F/4 = 5g ⇒ F = 200 N (5kg is lifted off)

F/4 =10g ⇒ F = 400 N(10kg is lifted off)

When F = 100 N

a₁ = a₂ = 0
When F = 300 N

a₂ = 0 ; F/4 50 = 5 a₁ ⇒ a₁ = 5m / sec²
When F = 500 N

Q.6. A man in a lift ascending with an upward acceleration a throws a ball vertically upwards with a velocity v and catches it after t₁ second. Afterwards, when the lift is descending with the same acceleration a acting downwards, the man again throws the ball vertically upwards with the same velocity and catches it after t₂ seconds. Which of the following statements are correct?
(a) The velocity of the ball is g ( t₁ + t₂ )/t₁t2
(b) The velocity of the ball is gt₁t₂/( t₁ + t₂)
(c) The acceleration of the ball is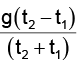
(d) The acceleration of the ball is

Correct Answer is option (b and c)

Q.7. In the figure, a man of true mass M is standing on a weighing machine placed in a cabin. The cabin is joined by a string with a body of mass m. Assuming no friction, and negligible mass of cabin and weighing machine, the measured mass of man is (normal force between the man and the machine is proportional to the mass)

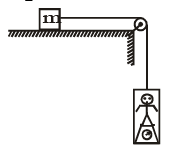(a) measured mass of man is Mm/(M + m)
(b) acceleration of man is mg/(M + m)
(c) acceleration of man is Mg/(M + m)
(d) measured mass of man is M.

Correct Answer is option (a and c)
Mg – T = Ma …(i)
T = ma …(ii)
Solving (i) and (ii)
a = mg/(M + m)
FBD of man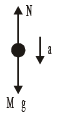
 

Mg – N = Ma
N = Mmg(M + m)

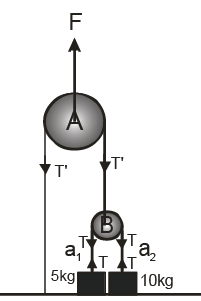
Q.8. Figure shows two blocks A and B connected to an ideal pulley string system. In this system when bodies are released then (neglect friction and take g = 10 m/s²)

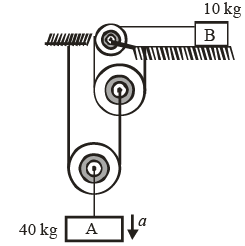(a) Acceleration of block A is 1 m/s²
(b) Acceleration of block A is 2 m/s²
(c) Tension in string connected to block B is 40 N
(d) Tension in string connected to block B is 80 N

Correct Answer is option (b and d)

Applying NLM on 40 kg block 400 – 4T = 40 a
For 10 kg block T = 10.4 a
Solving α = 2 m/s²
T = 80 N

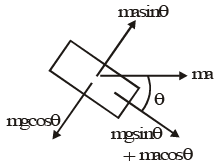
Q.9. The system of two blocks is at rest as shown in the figure. A variable horizontal force is applied on the upper block. The co–efficient of friction for both the contacts is m. Choose the correct option(s)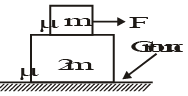
(a) When acceleration of the upper block is 2 mg net force on the lower block by the ground in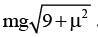
(b) When acceleration of the upper block is 2 mg acceleration of the lower block is zero.
(c) Net horizontal force on the lower block is always zero.
(d) Unless the upper block moves, no frictional force exists between the ground and the lower block.

Correct Answer is option (a, b and c)
∵ (f1)_max = μmg < (f₂)_max
2m will not move.

When acceleration of m is 2μg then
F = 3 μmg and f₁ = μmg.
∴ Total force on (2m) by ground

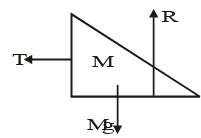
Q.10. The figure shows a block of mass m placed on a smooth wedge of mass M. Calculate the value of M' and tension in the string, so that the block of mass m will move vertically downward with acceleration 10 m/s² (Take g = 10 m/s²)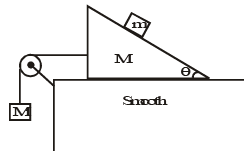
(a) the value of M' is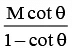

(b) the value of M¢ is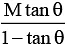

(c) the value of tension in the string is Mg/tan θ

(d) the value of tension is μg/ cot θ

Correct Answer is option (a, b and c)

M ' g - T= M ' a    ... (i)
T = Ma     ... (i)
M ' g = a(M + M ')

ma sin θ = mg cos θ
a = g cot θ

g cot θ =  (M 'g/M + M)

cot θ M + cot θM ' = M '

T = M a
= M. g cot θ
T = Mg/tan θ