JEE Advanced (Single Correct Type): Properties of Solids & Liquids | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A sample of metal weighs 210 gm in air, 180 gm in water and 120 gm in a liquid. Then relative density of
(a) metal is 3
(b) metal is 7
(c) liquid is 7
(d) liquid is 1/3
Correct Answer is option (b)
W¢ = v(ρm-σW)g
180= V(ρm-σW)g . . . (1)
120 = V(ρm-σl)g. . . (2)
210 = Vρmg . . . (3)
From (1) and (3)
From (2) and (3). . . (4)
From (1), (2) and (3)
Hence, B is correct.
Q.2. A vessel with a body floating in it falls with an acceleration a < g. Choose the correct statement.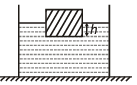
(a) h sill change continuously
(b) h will increase
(c) h will remain unchanged
(d) h will change continuously
Correct Answer is option (c)
ρBodyvg = ρwv'g
This is independent of the value of effective g.
Q.3. In which case the wire has maximum expansion, if the same force is applied to each wire
(a) L = 500 cm, d = 0.05 mm
(b) L = 200 cm, d = 0.02 mm
(c) L = 300 cm, d = 0.03 mm
(d) L = 400 cm, d = 0.01 mm
Correct Answer is option (d)
(Y and F are constant)
The maximum expansion occurs in the wire for which the ratio L/r2 will be maximum.
Q.4. A lead ball at 30°C is dropped from a height of 6.2 km. The ball is heated due to the air resistance and it completely melts just before reaching the ground. The molten substance falls slowly on the ground. Calculate the latent heat of fusion of lead. Specific heat capacity of lead = 126 J/kg–°C and melting point of lead = 330°C. Assume that any mechanical energy lost is used to heat the ball. Use g = 10 m/s2.
(a) 22 kJ/kg
(b) 14 kJ/kg
(c) 20 kJ/kg
(d) 24 kJ/kg
Correct Answer is option (d)
The initial gravitational potential energy of the ball = mgh
= m × (10 m/s2) (6.2 × 103 m)
= m × (6.2 × 104 m2/s2) = m × (6.2 × 104 J/kg).
All this energy is used to heat the ball as it reaches the ground with a small velocity. Energy required to take the ball from 30°C to 330°C is
m × (126 J/kg–°C) × (300°C)
= m × 37800 J/kg
and energy required to melt the ball at 330°C = mL
Where, L = latent heat of fusion of lead
Thus, m × (6.2 × 104 J/kg) = m × 37800 J/kg + mL or, L = 24 kJ/kg.
Q.5. An electric heater is used in a room of total wall area 137 m2 to maintain a temperature of 20°C inside it, when the outside temperature is –10°C. The walls have three different layers of materials. The innermost layer is of wood of thickness 2.5 cm, the middle layer is of cement of thickness 1.0 cm and the outermost layer is of brick of thickness 25.0 cm. Find the power of the electric heater. Assume that there is no heat loss through the floor and the ceiling. The thermal conductivities of wood, cement and brick are 0.125 W/m-°C, 1.5 W/m-°C and 1.0 W/m–°C respectively.
(a) 7000 W
(b) 8000 W
(c) 9000 W
(d) None of these
Correct Answer is option (c)
The situation is shown in figure.
The thermal resistances of the wood, the cement and the brick layers are
As the layers are connected in series, the equivalent R = Rw + RC + RB°C/W = 3.33 × 10–3 °C/W
The heat current is= 9000 W
The heater must supply 9000 W to compensate the outflow of heat.
Q.6. A water tank filled with water and closed from the top is accelerating on the ground with acceleration a. Find the pressure at point A.
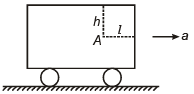
(a) ρgh + ρlα
(b) ρatm + ρgh + ρlα
(c) Patm + ρgh
(d) Patm + ρlα
Correct Answer is option (c)
PA = Patm + ρgh + ρlα
Q.7. A ring of radius r made of lead wire is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring. What is the minimum angular speed at which ring ruptures? [Given, σ is the tensile strength and ρ is density of lead]
(a) 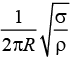
(b) 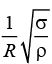
(c) 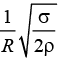
(d) 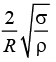
Correct Answer is option (b)
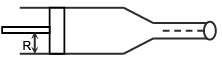
Q.8. A piston of a syringe pushes a liquid with a speed of 1 cm/sec. The radii of the syringe tube and the needle are R = 1cm and r = 0.5 mm respectively. The velocity of the liquid coming out of the needle is:
 (a) 2 cm/sec
(a) 2 cm/sec
(b) 400 cm/sec
(c) 10 cm/sec
(d) None of these.
Correct Answer is option (b)
According to the equation of continuity,Av = av'
⇒ v' = (A/a)v
Where A = πR2 and a = πr2.⇒
(1 cm/sec) = 400 cm/sec.
Q.9. Find the increase in density, at a depth of 1000 m below the surface of the water in the ocean. [Density of water at the surface of ocean is 1000 kg/m3 and the bulk modulus of water = 2 × 109 N/m2 and g = 10 m/s2]
(a) 5 kg/m3
(b) 4 kg/m3
(c) 2 kg/m3
(d) 1 kg/m3
Correct Answer is option (a)
m = ρv
Mass is constant,
0 = ρdv + vdρ
Q.10. Water rises to a height of 10cm in a capillary tube and mercury falls to a depth of 3.42 cm in the same capillary tube. If the density of mercury is 13.6g/cc and the angle of contact of mercury and water are 135° and 0° respectively, the ratio of surface tension of water and mercury is

(a) 1 : 0.15
(b) 1 : 3
(c) 1 : 6.5
(d) 1.5 : 1
Correct Answer is option (a)
Putting the values, we obtain 1: 6.5
Q.11. The excess pressure of one soap bubble in four times than other. Then the ratio of volume of the first bubble to another is
(a) 1: 64
(b) 1: 4
(c) 64: 1
(d) 1: 2
Correct Answer is option (a)
Q.12. The figure shows a model of perfume atomizer. When the bulb A is compressed, air (density ρa) flows through the narrow tube. Consequently pressure at the position of the vertical tube reduces. The liquid (perfume) rises in through the vertical tube and emerges through the end. If the excess pressure applied to the bulb in this process be Δp then the minimum speed of air in the tube to lift the perfume is: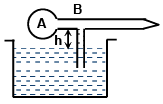 (a)
(a) 
(b) 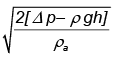
(c) 
(d) None of these
Correct Answer is option (a)
Applying Bernoulli’s principle at 1 and 2, we obtain
Putting v1 = 0 since the air is at rest inside the bulb,
P1 = P0 + Δp, P2 = P0 - ρgh, where ρ = density of liquid (perfume)
ρa = density of air
v2 = minimum velocity of air to lift the liquid through the height h = v (say)
pa = atmospheric pressure
We obtain, v =
Q.13. A liquid flows out of a large vessel through a narrow pipe. What is the pressure at point A in the narrow pipe which is at depth x from top level of water surface?
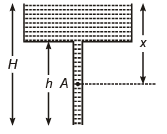
(a) patm – ρg(h - x)
(b) patm - ρg(H - x)
(c) patm + ρg(h - x)
(d) patm + ρgx
Correct Answer is option (b)
pA = pAtm – ρg(H - x)
Q.14. The density of ice is x gm/cc. and that of water is y gm/cc. What is the change in volume in cc., when m gm of ice melts?
(a) m(y – x)
(b) (y – x)/m
(c) mxy (x – y)
(d) m (-1/y + 1/x)
Correct Answer is option (d)
m = volume x density
Mass remains constant.
Q.15. There are two wires of same material and same length while the diameter of second wire is 2 times the diameter of first wire, then ratio of extension produced in the wires by applying same load will be
(a) 1: 1
(b) 2: 1
(c) 1: 2
(d) 4: 1
Correct Answer is option (d)
(F, L and Y are constant)
Q.16. A drop of water of volume V is pressed between the two glass plates so as to spread to an area A. If S is the surface tension, then normal force required to separate the glass plates is
(a) SA2/V
(b) 2SA2/V
(c) 4SA2/V
(d) SA2/2V
Correct Answer is option (d)
Force required to separate the glass plates
Q.17. A large number of water drops each of radius r combine to have a drop of radius R. If the surface tension is T and the mechanical equivalent of heat is J, then the rise in temperature will be
(a) 2T/rJ
(b) 3T/RJ
(c) 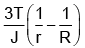
(d) 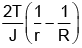
Correct Answer is option (c)
Rise in temperature, Δθ =(For water S = 1 and d = 1)
Q.18. In a surface tension experiment with a capillary tube water rises upto 0.1 m. If the same experiment is repeated on an artificial satellite, which is revolving around the earth, water will rise in the capillary tube upto a height of
(a) 0.1 m
(b) 0.2 m
(c) 0.98 m
(d) Full length of the capillary tube
Correct Answer is option (d)
In the satellite, the weight of the liquid column is zero. So the liquid will rise up to the top of the tube.
Q.19. A soap film of surface tension 3 x 10-2 Nm-1 formed in rectangular frame, can support a straw. The length of the film is 10 cm. Mass of the straw the film can support is
(a) 0.06gm
(b) 0.6gm
(c) 6gm
(d) 60gm
Correct Answer is option (b)
The weight of straw will be balanced by the force of surface tension ∴ mg = 2π ⇒ m = 2Tl/g
Q.20. If the work done in blowing a bubble of volume V is W, then the work done in blowing the bubble of volume 2V from the same soap solution will be
(a) W/2
(b) √2 W
(c)  W
W
(d)  W
W
Correct Answer is option (d)
Work done to form a soap bubble
W = 8πR2T (As V ∝ R3 ∴ R ∝ V1/3)
∴ W ∝ V2/3
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|

 . . . (4)
. . . (4)

 (Y and F are constant)
(Y and F are constant)

 °C/W = 3.33 × 10–3 °C/W
°C/W = 3.33 × 10–3 °C/W = 9000 W
= 9000 W


 (1 cm/sec) = 400 cm/sec.
(1 cm/sec) = 400 cm/sec.








 (F, L and Y are constant)
(F, L and Y are constant)


 (For water S = 1 and d = 1)
(For water S = 1 and d = 1)

















