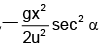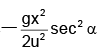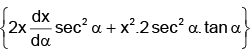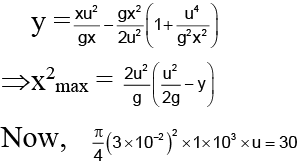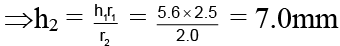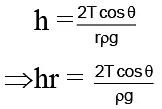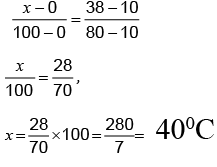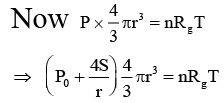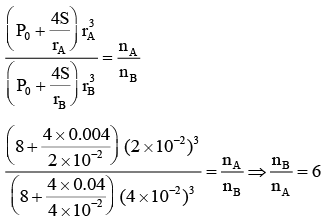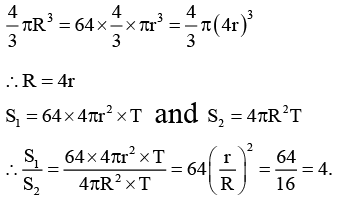Integer Answer Type Questions for JEE: Properties of Solids & Liquids | Chapter-wise Tests for JEE Main & Advanced PDF Download
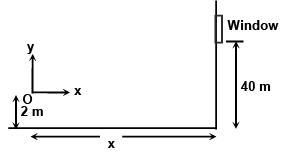
Q.1. A water jet directed by fireman must reach a window 40 m above the ground, from a nozzle of diameter 3 cm discharging 30 kg/s. Determine the largest distance from the building where a fireman can stand and still reach the jet into the window. The nozzle is at a height 2m above the ground.
Ans. 137
Taking O as the origin of coordinate system, the equation of the water jet is y = x tanα
Here, y = 38 (constant)
⇒ 38 = x tan α
Differentiating with respect to α, we get
0 = dx/dα tanα + x sec2 α - g/2u2
Now, for x to be maximum, dx/dα = 0 or, tan α = u2/gx
It can be shown that this value of a gives the maximum for x
⇒ u = 1200/9π m/s = 42.44 m/s
Putting this value of u and y = 38 m we get Xmax = 137 m.
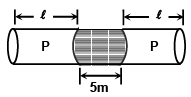
Q.2. A thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal ends containing air at the same pressure P. When the tube is held at an angle 60° with the vertical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in cm of mercury. (The temperature of the system is kept at 30°C)
Ans. 75.4
Length of pipe = (46 + 44.5 + 5) cm = 95.5 cm
Suppose the pressure in both the columns of air in the horizontal position be p.
∴ l = (46+44.5)/2 = 45.25 cm
When the tube is inclined, let p1 and p2 be the pressure and l1 and l2 be the lengths of lower and upper air columns respectively.
Using Boyle's law,
PAl = P1Al2 = P2Al2 (where A is area of cross-section of the tube)
Pl = P1l1 = P2l2 . . . (1)
P1 = P2 + ρHgg.lHg cos60°
(P2+ ρHgglHg cos60°)l1 = P2l2
[From equation (1)]cm of Hg column 5m
= 75.4 cm of Hg column
Q.3. Two long capillary tubes of diameter 5.0mm and 4.0 mm are held vertically inside water one by one. How much high the water will rise in each tube? (g = 10m/s2, surface tension of water = 7.0 x 10-2N/m.
Ans. 7
Height of water column in a capillary tube of radius r is given by
h = 2T cos θ/rpg ...(1)Where, T is surface tension, r is density and q is angle of contact of water-glass which can be assumed zero.
For the first tube, r = 2.5mm = 2.5 x 10-3m
∴ h == 5.6 mm
According to equation (1), for the same liquid, we have
∴ hr = 2T cos θ/ρg = constant
If a liquid rises to a height h1 in a capillary tube of radius r1 and to a height h2 in a capillary tube of radii r2, then Or h1r1 = h2r2
Q.4. Water rises in a capillary tube to a height 2.0 cm. In an another capillary whose radius is one-third of it, how much the water will rise? If the first capillary is inclined at an angle of 60° with the vertical then what will be the length of water column within the tube?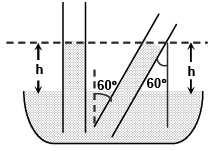
Ans. 4
Height of water column in a capillary tube of radius r is, in its vertical position, given by
or hr = constant (∴ T, q, r, g are constant)
In a capillary tube of radius one-third (r/3) water will rise more. Suppose it rises to a height
h' = 3hr/r = 3h = 3 x 2.0 = 6.0cm
When the first capillary is inclined at an angle of 60° to the vertical, the vertical height h( = 2.0) of the liquid will remain the same. Thus if the length of water column in the capillary be h¢ cm, then from figure, we get h' = h/cos 60° = 2.0/1/2 = 4.0cm
Q.5. The design of some physical instrument requires that there be a constant difference in length of 6 cm between an iron rod and copper rod laid side by side at all temperatures. Find their lengths.
(αFe = 11 × 10-60C-1, αCu = 17 × 10-6 °C-1)
Ans. 11
Since, the αCU > αFe so length of iron rod should be greater than the length of copper rod.
Let the initial lengths of iron and copper rods be l1 and l2 , then
l1 - l2 = 6 cm ..(i)
also since the difference has to be constant at all the temperatures, so
Δl = l1αFeΔT = l2αCuΔT
… (ii)
Solving (i) & (ii) we get
l1 = 17 cm and l2 = 11 cm
Q.6. The height of mercury column measured at t°= 400 C with a metallic scale which gives correct reading H1 = 100 cm at 0°C. What height H0 will the liquid column have at 0°C? The coefficient of linear expansion of brass is α = 0.03/ °C and the coefficient of volume expansion of mercury is γ = 0.05 / °C.
Ans. 20
H1 at t°C = H1 (1 + α t) actually since pressure is same, so
ρ0 gH0 = ρt gH1 (1 + αt)
H0 = H1 (1 + αt) ρt/ρ0 = H1 (1 + αt) (1 + γt)-1
H0 = H1 [1 + (α- γ) t] = 100[1+ (0.03 - 0.05)40] = 20 cm
Q.7. A thermometer has its lower and upper fixed points marked as 10° and 80° . When it reads 38° what is the corresponding temperature on Centigrade scale?
Ans. 40
Let x be the reading on Centigrade scale
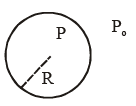
Q.8. Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8 N/m2. The radii of bubbles A and B are 2 cm and 4 cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. Find the ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity].
Ans. 6
Then P = P0 + 4S/r
For two bubbles
Q.9. Suppose that 64 raindrops combine into a single drop. Calculate the ratio of the total surface energy of the 64 drops to that of a single drop. Where T = 0.072 N/m
Ans. 4
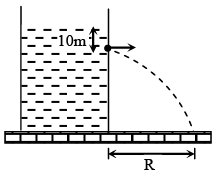
Q.10. A large tank is filled with water (density = 103kg/m3). A small hole is made at a depth 10 m below water surface. The range of water issuing out of the hole is R on ground. What extra pressure (in atm) must be applied on the water surface so that the range becomes 2R : (take 1 atm = 105 Pa and g = 10 m/s2)
Ans. 3
Range will become twice of velocity of efflux becomes twice. Now as,
v = √2gh
Therefore, h should become 4 times or 40 m
Thus, an extra pressure equivalent to 30 m of water should be applied.
1 atm = 0.76 × 13.6 m of water
= 10.336 m of water
30 m of water ≈ 3.0 atm
|
446 docs|929 tests
|