Integer Answer Type Questions for JEE: Moving Charges & Magnetism | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Find the magnetic induction B at a point on the axis due to an infinite thin conductor with semicircular cross-section of radius R = 10 cm carrying a uniform current i = π amp.
Ans. 4 μT
Let R be the radius of semicircular cross-section and O, a point on the axis. Considering an element dx1 carrying current di1Induction dB1 at O due to di1 is
This is directed normal to line joining the element to O.
Field dB2 due to corresponding element dx2 points in a direction shown. Resolving ,acting on same line and
acting on opposite direction and hence cancelling each other.
∴
Q.2. Two concentric coplanar semicircular conductors form part of two current loops as shown in the figure. If their radii are 11 cm and 4 cm calculate the magnetic induction at the centre.
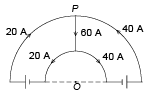
Ans. 50 μ
Magnetic induction at O =
=
=
= 50 μ weber/m2 (inward).
Q.3. Two particles P and Q, each having a mass M = 1 mg are placed at a separation D = 4 m in a uniform magnetic field B = 1 T as shown in figure. They have opposite charges of equal magnitude of 200 μC. At time t = 0 the particles are projected towards each other, each with a speed v. Suppose the coulomb force between the charges is switched off. Find the maximum value vm of the projection speed so that the two particles do not collide.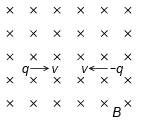
Ans. 40 cm/s
Force acting on P due to the magnetic field = Bqv. This particle P will describe a circle in the clockwise direction whose radius is obtained from the equation
The particle Q will describe a circle in the anticlockwise direction
The two particles do not collide if
Maximum value of the projection speed,
Q.4. A copper wire with crosssectional area 2.5 mm2 and bent to make three sides of a square can turn about a horizontal axis OO'. The wire is located in a uniform vertical magnetic field. Find the magnetic induction, if on passing a current I = 16 A deflects by an angle θ = 20°(Specific gravity of copper = 8.9).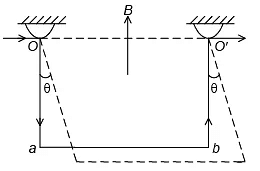
Ans. 9900 mμT
The deflection of the system is due to the force on the wire, due to the magnetic field B and the force is given by = BIa, where a is the side of the square and this force acts in the horizontal direction. The moment of the force about the axis of rotation OO'
BIa x a cosθ = Bla2cosq
where θ = 20°.
The weight of the wire is mg and this acts through the centre of gravity of the wire, G lying at a distance of a/2+a/6 = 2a/3 from OO'
∴ moment of the weight about OO'
=
For the equilibrium of the system
or
The mass m of the wire is given by
m = Length of the wire x cross-section x density
= 3a x (2.5 x 10–6 m2) (8900 kg/m3)
∴ B =
= 9900 μT
Q.5. A beam of protons with a velocity 4 x 105 m/sec enters a uniform magnetic field of 0.3 Tesla at an angle of 60o to the magnetic field. Find the radius of the helical path taken by the proton beam. Also find the pitch of the helix, which is the distance travelled by a proton in the beam parallel to the magnetic field during one period of rotation. [Mass of proton =1.67 x 10-27 Kg, charge on proton = 1.6 x 10-19 C]
Ans. 4.4 cm
The velocity of particle can be resolved into two components v cos 60o, parallel and v sin60° perpendicular to direction of B. Due to parallel component of velocity (= v cos 60°), Lorentz force on proton is zero. [F = q (v cos 60o) B sin 0° = 0]Due to perpendicular component of velocity ( = v sin 60o), Lorentz force on proton is
F = q (v sin 60o) B sin 90o = qv B sin 60o. This force is ⊥ to the plane of paper, directed into it. Due to this force, proton will move on a circular path, having axis along the direction of magnetic field. The radius of this circular path is given by
Due to simultaneous linear motion of proton along the direction of magnetic field, the proton will also move forward along the direction of B i.e. proton will spiral around the direction of . Hence, the radius of spiral or helical path is
= 1.205 x 10-2 m
Pitch of the helix = v cos 60o x T = v cos 60o x 2πr/v sin 60o
=
Q.6. A loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0T perpendicular to the plane of the loop. Show that when a current is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 amp.
Ans. 0.125N
Consider small elemental length of the loop when a current is passed through the loop in clock-wise direction and loop is placed in a downward magnetic field, thenforce on each element will be directed radially outward and ^ to the element. Hence the loop opens into a circle. Consider an element AB of length dl of the circle of radius r subtending an angle a at the centre O. If T is the tension in the wire, then force towards the centre will be equal to 2T sin (a/2) which is balanced by outward magnetic force on the current carrying element (= Bidl)
i.e. 2T sin(a/2) = Bidl
For small angle α, sin(α/2) = α/2
∴
we get
Q.7. A series LCR circuit containing a resistance of 120 Ώ has angular resonance frequency 4 × 105 rad/sec. At resonance the voltage across resistance and inductance are 60 V and 40 V respectively. At what frequency (in 105) the current in the circuit lags the voltage by 45o?
Ans. 8 x 105 rad / s
At resonance reactance X = 0
As,
or
L= 0.2 mH
At resonance
In LCR circuit,
or
Or
Or w =
= 8 x 105 rad / s
Q.8. A series LCR circuit with R = 20 Ώ, L = 1.5 H and C = 35 μF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in Kw transferred to the circuit in one complete cycle?
Ans. 2
When frequency of supply is equal to natural frequency,
Then,
Pav = 2000 watt = 2kW
Q.9. The magnetic field at all points within the cylindrical region whose cross – section is indicated in the accompanying figure starts increasing at a constant rate β. The induced electric field, E, satisfies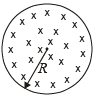 E ∝ rp (r < R) and E ∝ r–q (r > R)
E ∝ rp (r < R) and E ∝ r–q (r > R)
where r is the distance from the axis of the region. Find the value of p + q.
Ans. 2
Here, we shall discuss three situations i.e. when r lies inside, at the surface and outside the region
CASE I: For r ≤ R (inside):
Using,
⇒
⇒
∴ E ∝ r,
So, E –r graph is a straight line passing through origin.
CASE II: At r = R (at the surface)
∴
CASE III: For r ≥ R (outside)
Using,
⇒
⇒
∴
Q.9. A non–conducting ring of radius R having uniformly distributed charge Q starts rotating about x–x′ axis passing through diameter with an angular acceleration α as shown in the figure. Another small conducting ring having radius a (a << R) is kept fixed at the centre of bigger ring is such a way that axis xx′ is passing through its centre and perpendicular to its plane. If the resistance of small ring is r = 1Ω, find the induced current in it in ampere.
(Given 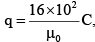 R = 1 m, a = 0.1 m, α = 8 rad/s2)
R = 1 m, a = 0.1 m, α = 8 rad/s2)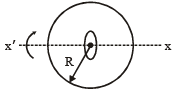
Ans. 8
ϕ = Bπa2
= 8 volt
i = 8 / 1 = 8 A.
Q.10. A uniform disc of radius r and mass m is charged uniformly with the charge q. This disc is placed flat on rough horizontal surface having coefficient of friction μ. A uniform magnetic field is present in a cylindrical region (a > r) but varying as kt3 as shown in figure. Find the time in second after which the disc beings to rotate. (Given r = 1 m, m = 18 kg, q = 1 C, μ = 0.1, K = 4, g = 10 m/s2)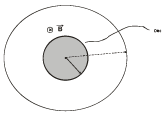
Ans. 2
Maximum torque due to friction force
dτ = µdmgx
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|

 Induction dB1 at O due to di1 is
Induction dB1 at O due to di1 is

 acting on same line and
acting on same line and  acting on opposite direction and hence cancelling each other.
acting on opposite direction and hence cancelling each other.














 Due to perpendicular component of velocity ( = v sin 60o), Lorentz force on proton is
Due to perpendicular component of velocity ( = v sin 60o), Lorentz force on proton is


 force on each element will be directed radially outward and ^ to the element. Hence the loop opens into a circle. Consider an element AB of length dl of the circle of radius r subtending an angle a at the centre O. If T is the tension in the wire, then force towards the centre will be equal to 2T sin (a/2) which is balanced by outward magnetic force on the current carrying element (= Bidl)
force on each element will be directed radially outward and ^ to the element. Hence the loop opens into a circle. Consider an element AB of length dl of the circle of radius r subtending an angle a at the centre O. If T is the tension in the wire, then force towards the centre will be equal to 2T sin (a/2) which is balanced by outward magnetic force on the current carrying element (= Bidl)




















































