Integer Answer Type Questions for JEE: Electrostatics | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. An electron is projected with a velocity of 1.186 x 107 m/s, at an angle q with the x-axis, towards a large metallic plate kept 0.44 mm away from the electron. The plate has a surface charge density -2 x 10-6 C/m2. Find the minimum value of q, for which it fails to strike the plate.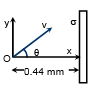
Ans. 60o
By law of conservation of energy,
⇒
Putting the values of s, m, v ande0, we get
cos2θ = 0.248
cosθ = 0.5
and θmin = 60°
Q.2. A small ball of mass 2 x 10-3 kg having a charge of 1 μC is suspended by a string of length 0.8 m. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity which should be imparted to the lower ball so that it can make complete revolution in a vertical circle. [Take g = 10 m/s2.]
Ans. 5.96 m/s
For looping the loop, at the highest point,
⇒ v2 = 3.5 (m/s)2 ......(i)
But the electrostatic work done when particle goes from bottom to top = 0
Hence,
⇒ u = √35.5 m/s = 5.96 m/s
Q.3. In the adjacent circuit, Each capacitor has a capacitance of 5 mF. Find the charge that will flow through MN when the switch S is closed.
Ans. 333.3 μC
When S is open:
Equivalent capacitance = C1 = 2C / 3
∴
When S is closed:
Equivalent capacitance = C2 = 2C
∴ Q2 = C2E = 2CE
∴ Charge flowing through MN =
=
= 333.3 μC
Q.4. Four charges + q, + q, – q and – q are placed respectively at the corners A, B, C and D of a square of side a = (√5 - 1) cm arranged in the given order. If E and P are the midpoints of sides BC and CD respectively, what will be the work done in carrying a charge q0 from O to E and from O to P?
(take q = 10 μC, q0 = 5 μC)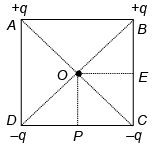
Ans. 36J
ABCD is the given square of side a. The charges are placed at the corners as shown. O is the midpoint of square.
OA = OB = OC = OD = r (say) = a/√2
Potential at O due to the charges at the corners
=
Therefore, O is at zero potential. The electric field at O due to charge at A
=along OC.
To find the work done in carrying a charge e from O to E
Potential at O = 0
Potential at E =
ince, AE = DE and BE = CE the summation in bracket vanishes. So potential at E = 0.
Hence no work is done in moving the charge from O to E.
To find the work done in carrying the charge from O to P
Potential at P =
Now, AP =
DP = a/2
Potential at P
Potential difference between O and P =
=
Work done in carrying a charge e from O to P =
J = 36 J
Q.5. A particle of positive charge Q = 8q0, is having a fixed position P. Another charged particle of mass m and charge q = 10 μC moves at a constant speed in a circle of radius r1 = 2 cm with centre at P. Find the work that must be done to increase the radius of circle to r2 = 4 cm.
Ans. 90J
Let q orbit round Q in a circle of radius r.
K.E. of orbiting particle = 1/2 mv2 ....... (i)
Where, v is orbital velocity.
Potential energy of q =
P.E. is negative since q is negative.
Electrostatic attraction on q =.... (iii)
This is used as centripetal force required for circular motion.
From (1) and (4)
Total energy of the orbiting charge
= K.E. + P.E.
=
The total energy of q when in orbit of radius r1
When it is in orbit of radius r2
The work done on q = change in energy
= E2 - E1
=
=
= 90 J
Q.6. A ball of mass m = 100 gm with a charge q can rotate in a vertical plane at the end of a string of length l = 1 m in a uniform electrostatic field whose lines of force are directed upwards. What horizontal velocity must be imparted to the ball in the upper position so that the tension in the string in the lower position of the ball is 15 times the weight of the ball? (given qE = 3 mg)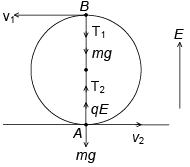
Ans. 50 m/s
As per principle of conservation of energy,
K.E. at B + P.E. at B = K.E. at A + P.E. at A.
Gain in K.E. = K.E. at A - K.E. at B
=
Loss in P.E. = P.E. at B - P.E. at A.
= loss in gravitational P.E. at B - gain in electrical energy at A
= mg(2 l ) - (qE) × 2l = (mg -qE)2 l … (ii)
P.E. at B - P.E. at A = K.E. at A - K.E. at B
i.e.,
Centripetal force at A =
From equation (3)
From equation (4)
Given in problem, T2= 15 mg
∴
or
or
Horizontal velocity to be imparted to the ball,= 50 m/s.
Q.7. Two capacitors are first connected in parallel and then in series. If the equivalent capacitances in the two cases are 16 F and 3 F, respectively, then capacitance of each capacitor is
Ans. 12 F, 4 F
Let C1 and C2 be the individual capacitance then C1 + C2 = 16 . . . .(i)
From (i) and (ii) C1 = 12 F, C2 = 4F
Q.8. Four identical charges, each of charge +q are placed at the terminals of each arm of a holy cross of Jesus Christ. Both side arms and the upper arm has length a and lower arm has length 2a. When a charge –Q is placed at the junction of cross it is found that the charge on upper arm is at equilibrium. If 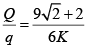 , find K. (Structure of the cross is assumed in vacuum)
, find K. (Structure of the cross is assumed in vacuum)
Ans. 3
Net force on upper on upper arm charge is
⇒ k = 3
Q.9. A solid conducting sphere of radius 10 cm is enclosed by a thin metallic shell of radius 20 cm. A charge q = 20 μC is given to the inner sphere. Find the heat generated in the process, the inner sphere is connected to the shell by a conducting wire (in J).
Ans. 9J
The whole charge is transferred to the outer sphere.
∴ Heat generated = Ui – Uf
Here C1 = 4πεoR1 and C2 = 4πεoR2
∴
= 9 J
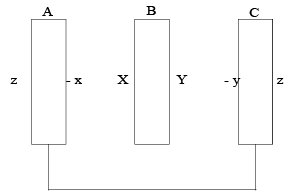
Q.10. In the fig shown there are three thin large metallic plates. the middle plate carries a total charge q = 5 μC. Plates 1 and 2 are connected by a wire. Find the charge induced on the outer surface of plate 1 and 2 in micro coulomb. given l1= 5cm, l2= 10cm .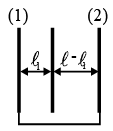
Ans. 2
Let the charge distribution in all the six faces be as shown in figure. We have used the fact that two opposite faces have equal and opposite charges on them . Net charge on the outer’s plate are zero
2z - x - y = 0
2z = x+ y.......(i)
For the A and C are at same potential.
Hence
VB - VA = VB - VC
Charge on the middle plate will conserve. Hence
x + y= q.............(iii)
From equation (ii) and (iii)
and
Put the values of 1,11 and q value then we will be getting
x = 2
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|










 along OC.
along OC.







 .... (iii)
.... (iii)
















 = 50 m/s.
= 50 m/s.