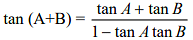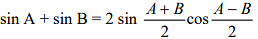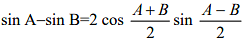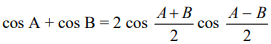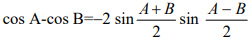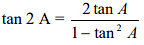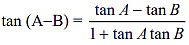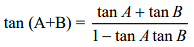| Table of contents |

|
| What is Angle? |

|
| System of Measurement of an Angle |

|
| Trigonometric Ratios |

|
| Some important Trigonometric Formulae |

|
- Welcome to the guide on the basics of trigonometry in physics! We'll be looking at three important trigonometric functions—sine, cosine, and tangent—and their reciprocal functions.
- In simple terms, we'll explore how these functions work and how they're used to solve problems involving vectors, forces, and waves in physics. Trigonometry might seem complex, but we aim to break it down into easy-to-understand concepts, making it a helpful tool for your journey into the world of physics.
 Application of Trigonometry
Application of Trigonometry
What is Angle?
- Consider a fixed straight-line OX. Let another straight line OA (called revolving line) be coinciding with OX rotate anticlockwise and take the position OA.
- The angle is measured by the amount of revolution that the revolving line OA undergoes in passing from its initial position to its final position.
- From the Figure given below, the angle covered by the revolving line OA is θ = ∠AOX.
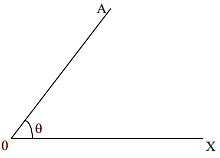 An Angle
An Angle
- An angle ∠AOX is +ve, if it is traced out in anticlockwise direction and ∠AOX is –ve, if it is traced out in clockwise direction
System of Measurement of an Angle
There are two systems for the measurement of an angle namely,
- Sexagesimal System
- Circular system
Sexagesimal System
In this system
1 right angle = 90o (degrees)
1 degree = 60’ (minutes)
1 minute = 60’’ (seconds)
Circular system
π (Radians) = 180° = 2 right angles
∴ 1 right angle = π/2 radians.
Let a particle move from the initial position A to the final position B along a circle of radius r as shown in the figure.
 Understanding Radians
Understanding Radians
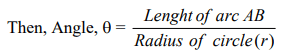 If the length of arc AB = radius of the circle (r), then θ = 1 radian.
If the length of arc AB = radius of the circle (r), then θ = 1 radian.
Radian: An angle subtended at the center of a circle by an arc whose length is equal to the
radius of the circle is called one radian.
Relation between Radian and Degree
When a body or a particle completes one rotation, then θ = 360° and distance traveled (circumference of a circle).
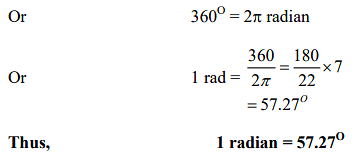
Example: Convert (-45°) into radians
Solution: -45 ⋅ 𝜋 /180 = −45𝜋 /180 = − 𝜋/4 radian
Example: Convert 3𝜋 /2 radian into degrees.
Solution: 3𝜋 /2 ⋅ (1 radian) 180 /𝜋 = 3𝜋 /2 ⋅ 180/ 𝜋 = 540𝜋/ 2𝜋 = 270°
Trigonometric Ratios
Consider triangle ONM in the four quadrants as shown below.
Consider two straight lines X'OX and Y'OY meeting at right angles in O. These two lines divide the plane into four equal parts called quadrants (figure given below).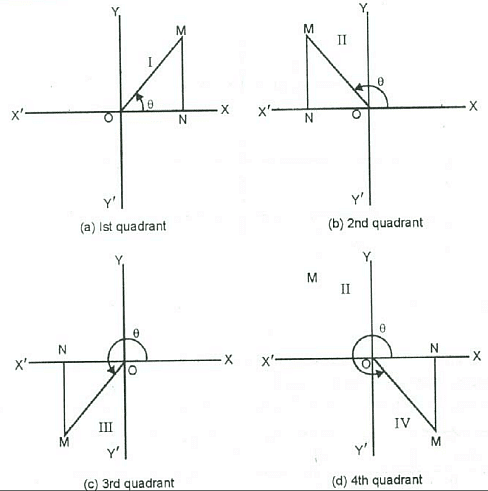 ΔONM in 4 Quadrants
ΔONM in 4 Quadrants
Now XOY, YOX', X'OY', and Y'OX are called I, II, III, and IV quadrants respectively. ON is +ve if drawn to the right side of O and −ve if drawn to the left side of O. MN is +ve if drawn above X'OX and −ve if drawn below X'OX.
Trigonometric Ratios of an Angle
 Trigonometric Ratios
Trigonometric Ratios
Example: A man observed a pole of height 60 ft. According to his measurement, the pole cast a 20 ft long shadow. Find the angle of elevation of the sun from the tip of the shadow using trigonometry.
Solution:
Let x be the angle of elevation of the sun, then
tan x = 60/20 = 3
x = tan-1(3)
or x = 71.56 degrees
Answer: The angle of elevation of the sun is 71.56º.
Important relations
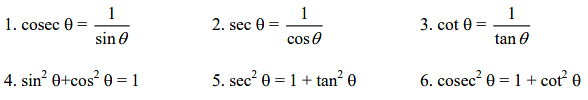
Signs of trigonometric ratios
 Trick to Remember Signs of Trigonometric Ratios
Trick to Remember Signs of Trigonometric Ratios
The signs of various trigonometric ratios can be remembered from the above figure.
Trigonometric Ratios of Standard angles
The trigonometric ratios of standard angles are given in the following table:
 Trigonometric Ratios of Standard Angles
Trigonometric Ratios of Standard Angles
Trigonometrical Ratios of Allied Angles
- (i) sin (−θ) = − sin θ (ii) cos (−θ) = cos θ (iii) tan (−θ) = − tan θ
- (i) sin (90°−θ) = cos θ (ii) cos (90°−θ) = sin θ (iii) tan (90°−θ) = cot θ
- (i) sin (90°+θ) = cos θ (ii) cos (90°+θ) = sin θ (iii) tan (90°+θ) = −cot θ
- (i) sin (180°−θ) = sin θ (ii) cos (180°−θ) = − cos θ (iii) tan (180°−θ) = − tan θ
- (i) sin (180°+θ) = −sin θ (ii) cos (180°+θ) = − cos θ (iii) tan (180°+θ) = − tan θ
- (i) sin (270°−θ) = − cos θ (ii) cos (270°−θ) = −sin θ (iii) tan (270°−θ) = cot θ
- (i) sin (270°+θ) = −cos θ (ii) cos (270°+θ) = sin θ (iii) tan (270°+θ) = −cot θ
Example:
Find the values of
(i) sin 270° (ii) sin 120° (iii) sin 120° (iv) tan (-30°)Solution: (i) sin 270° = sin (180° + 90°) = − sin 90° = −1
(ii) cos 120° = cos (90° + 30°) = − sin 30° = −1/2
(iii) sin 120° = sin (90° + 30°) = cos 30° =√3/2
(iv) tan (−30°) = − tan 30° = - 1/√3
Some important Trigonometric Formulae
- sin (A+B) = sin A cos B + cos A sin B
- cos (A+B) = cos A cos B − sin A sin B
- sin (A−B) = sin A cos B − cos A sin B
- cos (A−B) = cos A cos B + sin A sin B
- sin 2 A = 2 sin A cos A
- sin (A+B) sin (A−B) = sin2 A − sin2 B
- cos (A+B) cos (A−B) = cos2 A − sin2 B





- cos2A = cos2A - sin2A = 1 − 2sin2A = 2 cos2A −1



FAQs on Basics of Trigonometry - JEE
| 1. What is an angle? |  |
| 2. What is the system of measurement for angles? |  |
| 3. What are trigonometric ratios? |  |
| 4. What are some important trigonometric formulae? |  |
| 5. What are the basics of trigonometry for the JEE exam? |  |