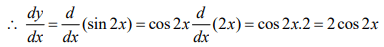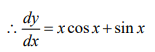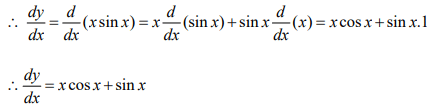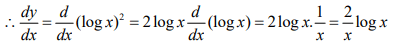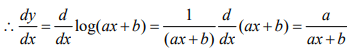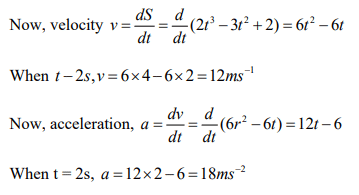What is a Function?
- If the value of a quantity y (say) depends on the value of another quantity x, then y is the function of x i.e. y = f(x).
- The quantity y is the dependent variable and the quantity x is the independent variable. For example, y = 2x2 + 4x + 7 is a function of x
(i) When x = 1, y = 2(1)2 + 4x1+7 = 13
(ii) When x = 2, y = 2(2)2 +4x2+7 = 23 - As the value of y depends on the value of x, y is the function of x.
Differential coefficient or derivative of a function
- Let y = f(x) …. (1)
That is, the value of y depends upon the value of x. - Let ∆x be a small increment in x, so that ∆y is the corresponding small increment in y, then
y + ∆y = f(x+∆x) …. (2) - Subtract (1) from (2), we get ∆y = f(x+∆x) − f(x)
- Divide both sides by ∆x
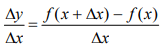
Where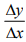 is called the average rate of change of y w.r.t. x.
is called the average rate of change of y w.r.t. x. - Let ∆x be as small as possible i.e. ∆x→0 (read as delta x tends to zero)
- Then, the differential coefficient or derivative of y w.r.t. x is
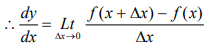
Theorems of Differentiations
- If y = C, when C is constant
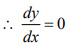
- If y = xn, where n is an integer
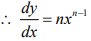
- If y = Cu, where u is the function of x and C is constant
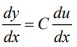
- If y = u ± v ± ω ± ……, where u, v and ω are the function of x
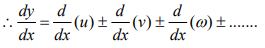
- If y = u v, where u and v are the function of x, then
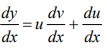
- If y =v/u, where u and v are the function of x, then
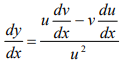
- If y = un, where u is the function of x then
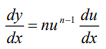
Differential coefficients of Trigonometric Functions
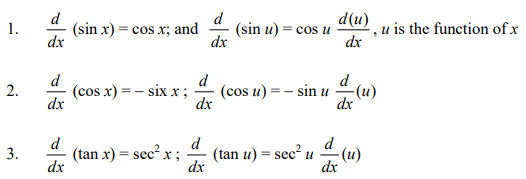
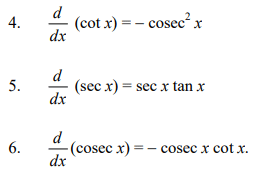
Example: Differentiate the following w.r.t. x.
(i) sin 2 x
(ii) x sin x(i) Let y = sin 2x
(ii) Let y = x sin x
Differential Coefficients of Logarithmic and Exponential Functions


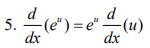
Example: Differentiate the follow w.r.t .x.
(i) 2 (loge x)2
(ii) log(ax + b)(i) Let y = (loge x)2
(ii) Let y = log(ax + b)
Example: If S = 2t3 - 3t2 + 2,find the position, velocity and acceleration of a particle at the end of 2s. S is measured in metre and t in second
S = 2t3 - 3t2 + 2
When t = 2s, S = 2 × 8 – 3 × 4 + 2 = 6 m
FAQs on Differentiation for Physics - JEE
| 1. What is differentiation in physics? |  |
Ans. Differentiation in physics refers to the mathematical operation used to determine the rate at which a physical quantity changes with respect to another quantity. It involves finding the derivative of a function, which represents the rate of change of the function at a particular point.
| 2. How is differentiation used in physics? |  |
Ans. Differentiation is extensively used in physics to analyze the behavior and properties of physical quantities. It helps in understanding how variables such as position, velocity, and acceleration are related to each other. By differentiating equations, scientists can determine the rate of change of various quantities and study the dynamics of systems.
| 3. Can differentiation be used to analyze motion in physics? |  |
Ans. Yes, differentiation plays a crucial role in analyzing motion in physics. By differentiating the equation of displacement with respect to time, we can obtain the equation for velocity. Similarly, differentiating the equation for velocity with respect to time gives the equation for acceleration. These derivatives help in understanding the motion of objects and their changing velocities.
| 4. What is the relationship between differentiation and kinematics? |  |
Ans. Differentiation and kinematics are closely related in physics. Kinematics deals with the description of motion, whereas differentiation is used to analyze the changing rates of motion. By applying differentiation to kinematic equations, we can determine the relationships between position, velocity, and acceleration. This allows us to understand the behavior of objects in motion.
| 5. How does differentiation help in solving physics problems? |  |
Ans. Differentiation helps in solving physics problems by providing a mathematical tool to analyze the changing rates of physical quantities. It allows us to determine the instantaneous rates of change, find relationships between different variables, and calculate important parameters like velocity and acceleration. By using differentiation techniques, scientists can model and predict the behavior of physical systems accurately.
Related Searches