JEE Advanced (One or More Correct Option): Straight Lines & pair of Lines | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The slope of the common tangents to the hyperbola 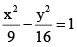 and
and 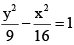 are
are
(a) –2, 2
(b) –1, 1
(c) 1, 2
(d) 2, 1
Correct Answer is option (b)
Given hyperbolas are…(i)
and…(ii)
Any tangent to (i) having slope m is…(iii)
Putting in (ii), we get…(iv)
If (iii) is a tangent to (ii), then the roots of (iv) are real and equal.
∴ Disc. = 032 x 32m2 (9m2 -16) = 4(16m2 - 9)(144m2 - 400) = 64(16m2 - 9)(9m2 - 25)
⇒ 16m2 (9m2 -16)= (l6m2 - 9)(9m2 - 25)
⇒ 144m4 - 256m2 = 144m4 - 481m2 + 225
⇒ 225m2 = 225 ⇒ m2 = 1 ⇒ m = +1
Hence, (B) is the correct answer
Q.2. The locus of the mid-points of the chords of the circle x2 + y2= 16 which are tangent to the hyperbola 9x 2 -16y2= 144 is
(A) ( x2 + y2 )2 = 16x2 - 9y2
(B) ( x2 + y2)2 = 9x2 - 16y2
(C) ( x2 - y2 )2 = 16x2 - 9 y2
(D) none of these
Correct Answer is option (a)
The given hyperbola is…(i)
Any tangent to (i) is y = mx +…(ii)
Let (x1 y1) be the mid-point of the chord of the circle x2 + y2 = 16 Then equation of the chord is t = s1
i.e. xx1 + yy1 -(x12 + y12 )= 0 ...(iii)
Since (ii) and (iii) represent the same line.
Hence, (A) is the correct answer.
Q.3. If PN is the perpendicular from a point on a rectangular hyperbola to its asymptotes, the locus, the mid-point of PN is
(a) circle
(b) parabola
(c) ellipse
(d) hyperbola
Correct Answer is option (d)
Let xy = c2 be the rectangular hyperbola, and let P (x1, y1) be a point on it. Let Q(h, k) be the mid-point of PN. Then the coordinates of Q are∴ x1 = h and y1/2 = k
⇒ x1 = h and y1 = 2k
But (x1, y1) lies on xy = c2
∴ h (2k) = c2 ⇒ hk = c2/2Hence, the locus of (h, k) is xy = c2/2, which is hyperbola
Hence, (D) is the correct answer.
Q.4. The asymptotes of xy = 4x + 3y are
(A) x = 4 y = 4
(B) x = 4 y = 3
(C) x = 3 y = 4
(D) x = 3 y = 3
Correct Answer is option (c)
We know that the combined equation of the asymptotes and the equation of the hyperbola differ by a constant.
∴ we can take the equations of the asymptotes as 0xy - 4x - 3y + k = 0
We have to find k such that the above equation a pair of straight lines
∴ abc + 2fgh-af2 -bg2 -ch2 = 0
Combined equation of the asymptotesxy - 4x - 3y +12 = 0
x(y - 4)-3(y - 4) = 0
⇒ (x - 3)(y - 4) = 0Hence, (C) is the correct answer.
Q.5. The sum of the reciprocals of the slopes of the tangents drawn from any point to the ellipse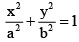 is 3, then the locus of the point is
is 3, then the locus of the point is
(a) 3y2 - 2xy - 3b2 = 0
(b) 3y2 + 2xy - 3b2 = 0
(c) y2 + xy - 3b2 = 0
(d) 2y2 + xy - b2 = 0
Correct Answer is option (a)
Any tangent to the ellipse is
Let it pass through (α, β)
Locus of (a, b) is 3y2 - 2xy - 3b2 = 0
Hence, (A) is the correct answer.
Q.6. A tangent to the ellipse 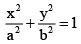 has slope 2 and makes an intercept √5 units on the auxiliary circle, then a focus of the ellipse is
has slope 2 and makes an intercept √5 units on the auxiliary circle, then a focus of the ellipse is
(a) 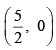
(b) (4, 0)
(c) (2, 0)
(d) (5, 0)
Correct Answer is option (a)
Equation to the tangent is
Auxiliary circle is x2 + y2 = a2 ; centre (0, 0) ; radius a
Let M be the mid-point
Hence (A) is the correct answer.
Q.7. The locus of the point of intersection of the tangents at the ends whose eccentric angle differ by a is
(a) 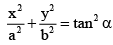
(b) 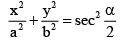
(c) 
(d) 
Correct Answer is option (b)
Let θ and ϕ be the eccentric angels of the two points.
Given ϕ - θ = α
ϕ = α + θ
Equation to the tangent at θ… (i)
II tangent is
Already
Squaring and adding,
Hence, (B) is the correct answer.
Q.8. Let P be a variable point on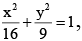 then the maximum area of SPS' , where S and S' are the foci is
then the maximum area of SPS' , where S and S' are the foci is
(a) 37
(b) 27
(c) 7
(d) 47
Correct Answer is option (a)
Area of
Maximum value of sin θ = 1
Maximum area = 3√7
Hence, (A) is the correct answer.
Q.9. Tangents are drawn from the point P(–2, 6) to the parabola y2 8x = meet it at A and B. Then the locus of the centre of the circle described on AB as diameter is
(a) y2 = x- 2
(b) y2 = 2 ( x- 2)
(c) y2 = 3(x - 2)
(d) y2 = 4(x - 2)
Correct Answer is option (d)
4a = 8 a = 2
Directrix is x = - a
x = - 2
∴ P is a point on the directrix.
Theory: Perpendicular tangents intersect on the directrix. tangents at A (t1) and B (t2) are perpendicular
Now mid-point of
This is the required centre.
Let it be (a, b)
Now
= 4[α + 2(- 1)]
= 4(α - 2)
Locus of (α, β) is y2 = 4(x - 2)
Hence, (D) is the correct answer.
Q.10. The directrix of the parabola 4x = y2- 2y has the equation
(a) 4x -1= 0
(b) 4x + 5= 0
(c) 4x - 5= 0
(d) 4y + 5= 0
Correct Answer is option (b)
y2 - 2y = 4x
(y -1)2 -1 = 4x
Parabola with vertex
4a = 4 ⇒ a = 1
Equation to the directrix is
∴ Hence, (B) is the correct answer.
Q.11. The opposite angular points of a square are (3, 4) and (1, - 1). Then the co-ordinates of other two points are
(a)
(b)
(c)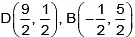
(d) None of these
Correct Answer is option (c)
Obviously, slope of AC = 5 / 2 .
Let m be the slope of a line inclined at an angle of 45º to AC,
then
Thus, let the slope of AB or DC be 3/7and that of AD or BC beThen equation of AB is 3x - 7y + 19 = 0.
Also the equation of BC is 7x + 3y - 4 = 0.
On solving these equations, we get,
Now let the coordinates of the vertex D be (h, k). Since the middle points of AC and BD are same, therefore
Q.12. If the lines y = 3x+ 1 and 2y = x+ 3 are equally inclined to the line y = mx+ 4, then m =
(a)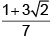
(b)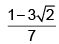
(c) 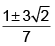
(d) 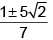
Correct Answer is option (d)
Let the angle between first and third line is θ1 and between second and third is θ2, then
Q.13. Let P(-1,0), Q(0, 0) and R (3, 3√3 ) be three points. Then the equation of the bisector of the angle PQR is
(a)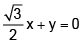
(b) x + √3y = 0
(c) √3x + y = 0
(d)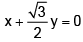
Correct Answer is option (c)
Clearly, ∠PQR= 120° OQ is the angle bisector of the angle, so line OQ makes 120° with the positive direction of x-axis.Therefore, equation of the bisector of ∠PQR is y = tan120° x or y =- √3x i.e., √3x + y= 0.
Q.14. If for a variable line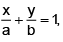 the condition
the condition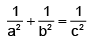 (c is a constant) is satisfied, then locus of foot of perpendicular drawn from origin to the line is
(c is a constant) is satisfied, then locus of foot of perpendicular drawn from origin to the line is
(a) x2 + y2= c2 / 2
(b) x2 + y2= 2c2
(c) x2 + y2= c2
(d) x2 - y2= c2
Correct Answer is option (c)
Equation of perpendicular drawn from origin to the line
[ ∵ m of given line
∴ m of perpendicular = a/b]
⇒ by - ax = 0
Now, the locus of foot of perpendicular is the intersection point of line
To find locus, squaring and adding (i) and (ii)
Q.15. If the circle x2 + y2 - 4x - 6y + k = 0 does not touch or intersect the axes and the point (2, 2) lies inside the circle, then
(a) 4 < k< 9
(b) 4 < k< 12
(c) 9 < k< 12
(d) none of these
Correct Answer is option (c)
The centre of the given circle is (2, 3) and the radius =
i.e.
Since the given circle does not touch or intersect the coordinate axes and the point
(2, 2) lies inside the circle
∴ x-cooridnate of centre> radius i.e.
y-coordinate of centre > radius i.e.and 4 + 4 -8 -12 +k < 0
⇒ 4 > 13 - k, 9 > 13 - k and -12 + k < 0
⇒ k > 9,k> 4 and k <12 ⇒ 9 <k<12
Q.16. If θ1,θ2 be the inclination of tangents drawn from the point P to the circle x2 + y2= a2 with x-axis, then the locus of P, it is given that cotθ1 cotθ2 = c , is
(a) c (x2 - a2 ) = 2xy
(b) c (x2 - a2 ) = y2 - a2
(c) c (y2 - a2 ) = 2xy
(d) none of these
Correct Answer is option (c)
Any tangent is
If it passes through p (h, k), then (k - mh)2 = a2 (1 + m2)
Q.17. The chord of contact of tangents from a point P to a circle passes through Q. If I1 and I2 are the lengths of the tangents from P and Q to the circle, then PQ is equal to
(a) 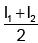
(b)
(c)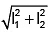
(d)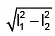
Correct Answer is option (c)
Let p (x1,y1) and Q (x2,y2) be two points and x2 + y2 = a2 be the given circle
then the chord of contact of tangents drawn from P to the given circle is
xx1 + yy1 = a2
It will pass through Q(x2, y2), if x2x1 + y2y1 = a2.. .(i)
Q.18. The circles x2 + y2 + 2g1x - a2 = 0 and x2 + y2 + 2g2x - a2 = 0 cut each other orthogonally. If p, p are perpendicular from (0, a) and (0, -a) on a common tangent of these circle, then p1p2 is equal to
(a)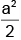
(b) a2
(c) 2a2
(d) a2 + 2
Correct Answer is option (b)
Given g1g2 + a2 = 0 . ..(i)
If lx + my = 1 is common tangent of these circle, then
So that g1g2 are the roots of the equation
Now,
Q.19. The equation of the line touching both the parabolas y2 = 4x and x2 = -32y is
(a) 2x + y - 4 = 0
(b) x + 2y + 4 = 0
(c) x - 2y + 4 = 0
(d) x - 2y - 4 = 0
Correct Answer is option (c)
Any tangent to y2 = 4x is
Solving with x2 = -32y
But the line is tangent to 2nd parabola.
Discriminant = 0
∴ the required common tangent is
2y = x + 4
x - 2y + 4 = 0.
Q.20. The algebraic sum of the ordinates of the points of intersection of a parabola and a circle is
(A) Proportional to the arithmetic mean of the radius and latus rectum
(B) zero
(C) equal to the ratio of radius and latus rectum
(D) 1
Correct Answer is option (b)
The equation to a circle is x2 + y2 + 2gx + 2fy + c = 0
Any point on the parabola y2 = 4ax is (at2,2at). If the circle and parabola intersect then
(at2 )2 + (2at )2 + 2g (at2)+ 2f (2at) + c = 0
a2t4 +12 (4a2 + 2ga)+ 4fat + c = 0This is a 4th degree equation in t giving 4 roots t1, t2, t3,t4.
∴ circle and parabola meet in 4 points2at1 + 2at2 + 2at3 + 2at4 = 0
Algebraic sum of the ordinates of the points of intersection = 0.Hence. (B) is the correct answer.
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|
 …(i)
…(i) …(ii)
…(ii) …(iii)
…(iii)
 …(iv)
…(iv) …(i)
…(i) …(ii)
…(ii)










 … (i)
… (i)
















 Then equation of AB is 3x - 7y + 19 = 0.
Then equation of AB is 3x - 7y + 19 = 0.








 ∴ m of perpendicular = a/b]
∴ m of perpendicular = a/b]


 i.e.
i.e.

 and 4 + 4 -8 -12 +k < 0
and 4 + 4 -8 -12 +k < 0


























