JEE Advanced (One or More Correct Option): Sequences & Series | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. If a, b, c are in A. P., and a2, b2, c2 are in H. P., then
(a) a = b = c
(b) 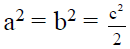
(c) a, b, c are in G. P.
(d) -a/2, b, c are in G.P
Correct Answer is option (a, c , d)
On solving we get a = cfrom b = a, a = b = c.
Q.2. The sum of three numbers which are consecutive terms of an A.P. is 21. If the second number is reduced by 1 while the third is increased by 1, three consecutive terms of a G.P. result. The three numbers is
(a) 3, 7, 11
(b) 12, 7, 2
(c) 1, 7, 11
(d) none of these
Correct Answer is option (a, b)
Let the three numbers in A.P. be a - d, a, a + d
Given (a - d) + a + (a + d) = 21
⇒ 3a = 21, ∴ a = 21 ÷ 3 = 7
∴ The numbers are 7 - d, 7, 7 + d
If the second number is reduced by 1 while the third number is increased by 1, the resulting numbers are 7 - d, 6, 8 + d which are given to be in G.P.⇒ 36 = (7 - d) (8 + d) ⇒ 36 = 56 - d - d2
⇒ d2 + d - 20 = 0
⇒ (d + 5) (d - 4) = 0 ∴ d = -5, 4
When d = -5
The numbers are 12, 7, 2
When d = 4, the numbers are 3, 7, 11.
Q.3. If a,a2 + 2,a3 +10 be three consecutive terms of G.P., then the fourth term is
(a) 0
(b) 6
(c) 729/16
(d) 54
Correct Answer is option (c, d)
The given equation can be written as
∴ Roots are real in any case and may be equal or unequal.
Q.4. If the first and the (2n -1)th term of an AP, GP and HP are equal and their nth terms are a, b and c respectively then
(a) a = b = c
(b) a ≥ b ≥ c
(c) a +c = b
(d) ac - b2 = 0
Correct Answer is option (a, b, d)
Since, first and (2n – 1)th terms are equal.
Let first term be x and (2n – 1)th term by y.Whose middle term is tn .
Thus in arithmetic progression;
In geometric progression;In harmonic progression;
⇒ b2 = ac and a> b > c (Using AM > GM > HM)
Here, equality holds (ie, a = b = c) only if all terms are same.
Hence, option (A), (B) and (D) are correct.
Q.5. Given that x + y+ z =15 when a, x, y, z, b are in A.P. , and 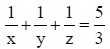 when a, x, y, z, b are in H.P. Then
when a, x, y, z, b are in H.P. Then
(a) G.M. of a and b is 3
(b) One possible value of a + 2b is 11
(c) A.M. or a and b is 6
(d) Greatest value of a - b is 8
Correct Answer is option (a, b, d)
⇒ a +b =10 .....(1)
⇒ ab = 9 .....(2)
From (1) & (2) a = 9, b = 1 or a = 1, b = 9
Hence, G.M. = √ab = 3, a + 2b = 11 or 19
Q.6. If a, b, c are in H.P., then the value of  is
is
(a) 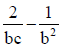
(b) 
(c) 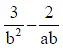
(d) none of these
Correct Answer is option (a, b, c)
As a, b, c are in H.P.
⇒ 1/a, 1/b, 1/c are in A.P.
Also,
from (i)
Also,
Q.7. If the first and (2n-1)th terms of an A.P; a G.P. and H.P. are equal and their nth terms are p, q and s respectively, then which of the following options is/are correct?
(a) p ≥ q ≥ s
(b) p+s = q
(c) ps = q2
(d) p = q = s
Correct Answer is option (a, c)
Let the first term be a and (2n-1)th term be b then
p, q, r are the A.M, G.M, H.M of a, b.
∴ p ≥ q ≥ r and ps = q2
Q.8. If log3, log(3x+2), log(3x+3) are in A.P. Then x is given by
(a) 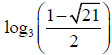
(b) 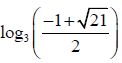
(c) 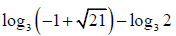
(d) 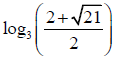
Correct Answer is option (b, c)
Q.9. The pth term Tp of HP is q(p + q) and qth term Tq is p (p + q) when p > 1, q > 1, (p ≠ q) then
(a) TP+Q = PQ
(b) TPQ = P+Q
(c) TP+Q > TPQ
(d) TPQ > TP+Q
Correct Answer is option (a, b, c)
Now, solving Eqs. (i) and (ii), we get
and
Q.10. If a1 ,a2 ,a3 .......,a24 be the terms of an A.P. such that a1 + a5+ a10 + a15 + a20 + a24 = 225, then
(a) a1 + a24 = 90
(b) a1+ a24 = 75
(c) S24 = 900
(d) S24 = 750
Correct Answer is option (b, c)
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|









 from (i)
from (i)



























